stringtranslate.com

Problema de satisfacibilidad booleana

En lógica y ciencias de la computación , el problema de satisfacibilidad booleano (a veces llamado problema de satisfacibilidad proposicional y abreviado SATISFIABILITY , SAT o B-SAT ) es el problema de determinar si existe una interpretación que satisfaga una fórmula booleana dada . En otras palabras, pregunta si las variables de una fórmula booleana dada pueden reemplazarse consistentemente por los valores VERDADERO o FALSO de tal manera que la fórmula evalúe VERDADERO. Si este es el caso, la fórmula se llama satisfacible . Por otro lado, si no existe tal asignación, la función expresada por la fórmula es FALSA para todas las asignaciones de variables posibles y la fórmula es insatisfacible . Por ejemplo, la fórmula " a AND NOT b " es satisfacible porque uno puede encontrar los valores a  = VERDADERO y b  = FALSO, lo que hace que ( a AND NOT b ) = VERDADERO. En contraste, " a AND NOT a " es insatisfacible.

SAT es el primer problema que se demostró que era NP-completo (el teorema de Cook-Levin) . Esto significa que todos los problemas de la clase de complejidad NP , que incluye una amplia gama de problemas de decisión natural y optimización, son, como mucho, tan difíciles de resolver como SAT. No se conoce ningún algoritmo que resuelva eficientemente cada problema SAT y, en general, se cree que no existe tal algoritmo, pero esta creencia no se ha demostrado matemáticamente y resolver la cuestión de si SAT tiene un algoritmo de tiempo polinomial es equivalente al problema P versus NP , que es un famoso problema abierto en la teoría de la computación.

Sin embargo, a partir de 2007, los algoritmos SAT heurísticos pueden resolver instancias de problemas que involucran decenas de miles de variables y fórmulas que consisten en millones de símbolos, [1] lo que es suficiente para muchos problemas SAT prácticos, por ejemplo, inteligencia artificial , diseño de circuitos , [2] y demostración automática de teoremas .

Definiciones

Una fórmula de lógica proposicional , también llamada expresión booleana , se construye a partir de variables , operadores AND ( conjunción , también denotada por ∧), OR ( disyunción , ∨), NOT ( negación , ¬) y paréntesis. Se dice que una fórmula es satisfacible si se puede hacer VERDADERA asignando valores lógicos apropiados (es decir, VERDADERO, FALSO) a sus variables. El problema de satisfacibilidad booleano (SAT) consiste en verificar, dada una fórmula, si es satisfacible. Este problema de decisión es de importancia central en muchas áreas de la informática , incluida la informática teórica , la teoría de la complejidad , [3] [4] la algoritmia , la criptografía [5] [6] y la inteligencia artificial . [7] [ cita(s) adicional(es) necesaria(s) ]

Forma normal conjuntiva

Un literal es una variable (en cuyo caso se denomina literal positivo ) o la negación de una variable (denominada literal negativo ). Una cláusula es una disyunción de literales (o un solo literal). Una cláusula se denomina cláusula de Horn si contiene como máximo un literal positivo. Una fórmula está en forma normal conjuntiva (CNF) si es una conjunción de cláusulas (o una sola cláusula).

Por ejemplo, x 1 es un literal positivo, ¬ x 2 es un literal negativo y x 1 ∨ ¬ x 2 es una cláusula. La fórmula ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 está en forma normal conjuntiva; sus cláusulas primera y tercera son cláusulas de Horn, pero su segunda cláusula no lo es. La fórmula es satisfacible, eligiendo x 1  = FALSO, x 2  = FALSO, y x 3 arbitrariamente, ya que (FALSO ∨ ¬FALSO) ∧ (¬FALSO ∨ FALSO ∨ x 3 ) ∧ ¬FALSO evalúa a (FALSO ∨ VERDADERO) ∧ (VERDADERO ∨ FALSO ∨ x 3 ) ∧ VERDADERO, y a su vez a VERDADERO ∧ VERDADERO ∧ VERDADERO (es decir, VERDADERO). Por el contrario, la fórmula CNF a ∧ ¬ a , que consta de dos cláusulas de un literal, es insatisfacible, ya que para a =VERDADERO o a =FALSO evalúa a VERDADERO ∧ ¬VERDADERO (es decir, FALSO) o FALSO ∧ ¬FALSO (es decir, nuevamente FALSO), respectivamente.

Para algunas versiones del problema SAT, es útil definir la noción de una fórmula de forma normal conjuntiva generalizada , es decir, como una conjunción de un número arbitrario de cláusulas generalizadas , siendo estas últimas de la forma R ( l 1 ,..., l n ) para alguna función booleana R y literales (ordinarios) l i . Diferentes conjuntos de funciones booleanas permitidas conducen a diferentes versiones del problema. Como ejemplo, R (¬ x , a , b ) es una cláusula generalizada, y R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R ( c , d ,¬ z ) es una forma normal conjuntiva generalizada. Esta fórmula se utiliza a continuación, siendo R el operador ternario que es VERDADERO solo cuando exactamente uno de sus argumentos lo es.

Utilizando las leyes del álgebra de Boole , cada fórmula de lógica proposicional puede transformarse en una forma normal conjuntiva equivalente, que, sin embargo, puede ser exponencialmente más larga. Por ejemplo, al transformar la fórmula ( x 1 ∧ y 1 ) ∨ ( x 2 ∧ y 2 ) ∨ ... ∨ ( x n ∧ y n ) en forma normal conjuntiva se obtiene

( x 1  ∨  x 2  ∨ … ∨  x n ) ∧
( y 1  ∨  x 2  ∨ … ∨  x norte ) ∧
( x 1  ∨  y 2  ∨ … ∨  x norte ) ∧
( y 1  ∨  y 2  ∨ … ∨  x norte ) ∧ ... ∧
( x 1  ∨  x 2  ∨ … ∨  y norte ) ∧
( y 1  ∨  x 2  ∨ … ∨  y norte ) ∧
( x 1  ∨  y 2  ∨ … ∨  y norte ) ∧
( y 1  ∨  y 2  ∨ … ∨  y n ) ;

mientras que el primero es una disyunción de n conjunciones de 2 variables, el último consta de 2 n cláusulas de n variables.

Sin embargo, con el uso de la transformación de Tseytin , podemos encontrar una fórmula de forma normal conjuntiva equisatisfacible con una longitud lineal en el tamaño de la fórmula de lógica proposicional original.

Complejidad

SAT fue el primer problema conocido como NP-completo , como lo demostró Stephen Cook en la Universidad de Toronto en 1971 [8] e independientemente por Leonid Levin en la Academia Rusa de Ciencias en 1973. [9] Hasta ese momento, el concepto de un problema NP-completo ni siquiera existía. La prueba muestra cómo cada problema de decisión en la clase de complejidad NP se puede reducir al problema SAT para fórmulas CNF [nota 1] , a veces llamadas CNFSAT . Una propiedad útil de la reducción de Cook es que preserva el número de respuestas aceptables. Por ejemplo, decidir si un gráfico dado tiene una coloración 3 es otro problema en NP; si un gráfico tiene 17 coloraciones 3 válidas, entonces la fórmula SAT producida por la reducción de Cook-Levin tendrá 17 asignaciones satisfactorias.

La NP-completitud solo se refiere al tiempo de ejecución de las instancias del peor caso. Muchas de las instancias que ocurren en aplicaciones prácticas se pueden resolver mucho más rápidamente. Consulte §Algoritmos para resolver SAT a continuación.

3-satisfacibilidad

La instancia 3-SAT ( x ∨ x ∨ y ) ∧ (¬ x ∨ ¬ y ∨ ¬ y ) ∧ (¬ x ∨ y ∨ y ) se reduce a un problema de camarilla . Los vértices verdes forman una camarilla de 3 y corresponden a la asignación satisfactoria x = FALSO, y = VERDADERO.

Al igual que el problema de satisfacibilidad para fórmulas arbitrarias, determinar la satisfacibilidad de una fórmula en forma normal conjuntiva donde cada cláusula está limitada a tres literales como máximo también es NP-completo; este problema se llama 3-SAT , 3CNFSAT o 3-satisfacibilidad . Para reducir el problema SAT sin restricciones a 3-SAT, transforme cada cláusula l 1 ∨ ⋯ ∨ l n en una conjunción de n - 2 cláusulas

( l 1 ∨ l 2 ∨ x 2 ) ∧
(¬ x 2 ∨ l 3 ∨ x 3 ) ∧
(¬ x 3 ∨ l 4 ∨ x 4 ) ∧ ⋯ ∧
(¬ x n −3 ∨ l n −2 ∨ x n −2 ) ∧
(¬ x n −2 ∨ l n −1 ∨ l n )

donde x 2 , ⋯ ,  x n −2 son variables nuevas que no aparecen en ningún otro lugar. Aunque las dos fórmulas no son lógicamente equivalentes , son equisatisfacibles . La fórmula resultante de transformar todas las cláusulas es como máximo 3 veces más larga que su original; es decir, el crecimiento de longitud es polinomial. [10]

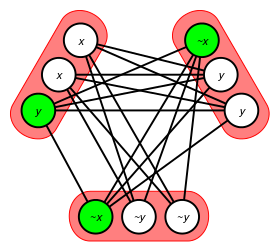
3-SAT es uno de los 21 problemas NP-completos de Karp , y se utiliza como punto de partida para demostrar que otros problemas también son NP-difíciles . [nota 2] Esto se hace mediante reducción en tiempo polinomial de 3-SAT al otro problema. Un ejemplo de un problema en el que se ha utilizado este método es el problema de la camarilla : dada una fórmula CNF que consta de c cláusulas, el gráfico correspondiente consta de un vértice para cada literal y una arista entre cada dos literales no contradictorios [nota 3] de diferentes cláusulas; vea la imagen. El gráfico tiene una c -camarilla si y solo si la fórmula es satisfacible. [11]

Existe un algoritmo aleatorio simple debido a Schöning (1999) que se ejecuta en el tiempo (4/3) n donde n es el número de variables en la proposición 3-SAT, y tiene éxito con alta probabilidad en decidir correctamente 3-SAT. [12]

La hipótesis del tiempo exponencial afirma que ningún algoritmo puede resolver 3-SAT (o, de hecho, k -SAT para cualquier k > 2 ) en tiempo exp( o ( n )) (es decir, fundamentalmente más rápido que el exponencial en n ).

Selman, Mitchell y Levesque (1996) proporcionan datos empíricos sobre la dificultad de las fórmulas 3-SAT generadas aleatoriamente, en función de sus parámetros de tamaño. La dificultad se mide en número de llamadas recursivas realizadas por un algoritmo DPLL . Identificaron una región de transición de fase desde fórmulas casi con certeza satisfacibles a fórmulas casi con certeza insatisfacibles en una relación cláusulas-variables de aproximadamente 4,26. [13]

La 3-satisfacibilidad se puede generalizar a k-satisfacibilidad ( k-SAT , también k-CNF-SAT ), cuando se consideran fórmulas en CNF con cada cláusula conteniendo hasta k literales. [ cita requerida ] Sin embargo, dado que para cualquier k ≥ 3, este problema no puede ser más fácil que 3-SAT ni más difícil que SAT, y los dos últimos son NP-completos, entonces debe ser k-SAT.

Algunos autores restringen k-SAT a fórmulas CNF con exactamente k literales . [ cita requerida ] Esto tampoco conduce a una clase de complejidad diferente, ya que cada cláusula l 1 ∨ ⋯ ∨ l j con j < k literales se puede rellenar con variables ficticias fijas a l 1 ∨ ⋯ ∨ l j ∨ d j +1 ∨ ⋯ ∨ d k . Después de rellenar todas las cláusulas, se deben agregar 2 k –1 cláusulas adicionales [nota 4] para garantizar que solo d 1 = ⋯ = d k = FALSE pueda conducir a una asignación satisfactoria. Dado que k no depende de la longitud de la fórmula, las cláusulas adicionales conducen a un aumento constante de la longitud. Por la misma razón, no importa si se permiten literales duplicados en las cláusulas, como en ¬ x ∨ ¬ y ∨ ¬ y .

Casos especiales del SAT

Forma normal conjuntiva

La forma normal conjuntiva (en particular, con 3 literales por cláusula) suele considerarse la representación canónica de las fórmulas SAT. Como se muestra arriba, el problema general de SAT se reduce a 3-SAT, el problema de determinar la satisfacibilidad de las fórmulas en esta forma.

Forma normal disyuntiva

SAT es trivial si las fórmulas se limitan a aquellas en forma normal disyuntiva , es decir, son una disyunción de conjunciones de literales. Una fórmula de este tipo es, de hecho, satisfacible si y solo si al menos una de sus conjunciones es satisfacible, y una conjunción es satisfacible si y solo si no contiene tanto x como NOT x para alguna variable x . Esto se puede comprobar en tiempo lineal. Además, si se limitan a estar en forma normal disyuntiva completa , en la que cada variable aparece exactamente una vez en cada conjunción, se pueden comprobar en tiempo constante (cada conjunción representa una asignación satisfactoria). Pero puede llevar tiempo y espacio exponenciales convertir un problema SAT general a forma normal disyuntiva; para obtener un ejemplo, intercambie "∧" y "∨" en el ejemplo de explosión exponencial anterior por formas normales conjuntivas.

Exactamente-1 3-satisfacibilidad

Izquierda: Reducción de Schaefer de una cláusula 3-SAT x ∨ y ∨ z . El resultado de R es VERDADERO (1) si exactamente uno de sus argumentos es VERDADERO, y FALSO (0) en caso contrario. Se examinan las 8 combinaciones de valores para x , y , z , una por línea. Las nuevas variables a ,..., f pueden elegirse para satisfacer todas las cláusulas (exactamente un argumento verde para cada R ) en todas las líneas excepto la primera, donde x ∨ y ∨ z es FALSO. Derecha: Una reducción más simple con las mismas propiedades.

Una variante del problema de 3-satisfacibilidad es el 3-SAT uno-en-tres (también conocido como 1-en-3-SAT y exactamente-1 3-SAT ). Dada una forma normal conjuntiva con tres literales por cláusula, el problema es determinar si existe una asignación de verdad a las variables de modo que cada cláusula tenga exactamente un literal VERDADERO (y, por lo tanto, exactamente dos literales FALSO). Por el contrario, el 3-SAT ordinario requiere que cada cláusula tenga al menos un literal VERDADERO. Formalmente, un problema 3-SAT uno-en-tres se da como una forma normal conjuntiva generalizada con todas las cláusulas generalizadas utilizando un operador ternario R que es VERDADERO solo si exactamente uno de sus argumentos lo es. Cuando todos los literales de una fórmula 3-SAT uno-en-tres son positivos, el problema de satisfacibilidad se llama 3-SAT positivo uno-en-tres .

El 3-SAT uno en tres, junto con su caso positivo, se enumera como problema NP-completo "LO4" en la referencia estándar Computers and Intractability: A Guide to the Theory of NP-Completeness de Michael R. Garey y David S. Johnson . Thomas Jerome Schaefer demostró que el 3-SAT uno en tres es NP-completo como un caso especial del teorema de dicotomía de Schaefer , que afirma que cualquier problema que generalice la satisfacibilidad booleana de una determinada manera está en la clase P o es NP-completo. [14]

Schaefer ofrece una construcción que permite una fácil reducción en tiempo polinomial de 3-SAT a 3-SAT de uno en tres. Sea "( x o y o z )" una cláusula en una fórmula 3CNF. Agregue seis nuevas variables booleanas a , b , c , d , e y f , que se utilizarán para simular esta cláusula y ninguna otra. Entonces la fórmula R ( x , a , d ) ∧ R ( y , b , d ) ∧ R ( a , b , e ) ∧ R ( c , d , f ) ∧ R ( z , c , FALSO) es satisfacible por algún ajuste de las nuevas variables si y solo si al menos una de x , y o z es VERDADERA, vea la imagen (izquierda). Por lo tanto, cualquier instancia 3-SAT con m cláusulas y n variables puede convertirse en una instancia 3-SAT equisatisfacible uno en tres con 5 m cláusulas y n + 6 m variables. [15] Otra reducción involucra solo cuatro variables nuevas y tres cláusulas: R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R( c , d ,¬ z ), ver imagen (derecha).

3-satisfacibilidad no todos iguales

Otra variante es el problema de 3-satisfacibilidad de no todos iguales (también llamado NAE3SAT ). Dada una forma normal conjuntiva con tres literales por cláusula, el problema es determinar si existe una asignación a las variables tal que en ninguna cláusula los tres literales tengan el mismo valor de verdad. Este problema también es NP-completo, incluso si no se admiten símbolos de negación, según el teorema de dicotomía de Schaefer. [14]

SAT lineal

Una fórmula 3-SAT es SAT lineal ( LSAT ) si cada cláusula (vista como un conjunto de literales) interseca como máximo una cláusula más y, además, si dos cláusulas se intersecan, entonces tienen exactamente un literal en común. Una fórmula LSAT se puede representar como un conjunto de intervalos semicerrados disjuntos en una línea. Decidir si una fórmula LSAT es satisfacible es NP-completo. [16]

2-satisfacibilidad

SAT es más fácil si el número de literales en una cláusula está limitado a 2 como máximo, en cuyo caso el problema se llama 2-SAT . Este problema se puede resolver en tiempo polinomial y, de hecho, es completo para la clase de complejidad NL . Si además todas las operaciones OR en literales se cambian a operaciones XOR , entonces el resultado se llama 2-satisfacibilidad de OR exclusivo , que es un problema completo para la clase de complejidad SL = L.

Satisfacción del cuerno

El problema de decidir la satisfacibilidad de una conjunción dada de cláusulas de Horn se llama satisfacibilidad de Horn o HORN-SAT . Se puede resolver en tiempo polinomial mediante un solo paso del algoritmo de propagación unitaria , que produce el modelo mínimo único del conjunto de cláusulas de Horn (con respecto al conjunto de literales asignados a TRUE). La satisfacibilidad de Horn es P-completa . Puede verse como la versión de P del problema de satisfacibilidad booleano. Además, decidir la verdad de las fórmulas de Horn cuantificadas se puede hacer en tiempo polinomial. [17]

Las cláusulas de Horn son interesantes porque pueden expresar la implicación de una variable a partir de un conjunto de otras variables. De hecho, una de esas cláusulas ¬ x 1 ∨ ... ∨ ¬ x n ∨ y puede reescribirse como x 1 ∧ ... ∧ x n → y ; es decir, si x 1 ,..., x n son todas VERDADERAS, entonces y también debe ser VERDADERA.

Una generalización de la clase de fórmulas de Horn es la de fórmulas de Horn renombrables, que es el conjunto de fórmulas que se pueden poner en forma de Horn reemplazando algunas variables con su respectiva negación. Por ejemplo, ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 no es una fórmula de Horn, pero se puede renombrar como fórmula de Horn ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ ¬ y 3 ) ∧ ¬ x 1 introduciendo y 3 como negación de x 3 . Por el contrario, ningún cambio de nombre de ( x 1 ∨ ¬ x 2 ∨ ¬ x 3 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 conduce a una fórmula de Horn. La comprobación de la existencia de dicho reemplazo se puede realizar en tiempo lineal; por lo tanto, la satisfacibilidad de dichas fórmulas está en P, ya que se puede resolver realizando primero este reemplazo y luego comprobando la satisfacibilidad de la fórmula de Horn resultante.

Satisfacción XOR

Otro caso especial es la clase de problemas donde cada cláusula contiene XOR (es decir, o exclusivo ) en lugar de operadores OR (simples). [nota 5] Esto es en P , ya que una fórmula XOR-SAT también puede verse como un sistema de ecuaciones lineales módulo 2, y puede resolverse en tiempo cúbico por eliminación gaussiana ; [18] vea el recuadro para ver un ejemplo. Esta reformulación se basa en el parentesco entre las álgebras de Boole y los anillos de Boole , y el hecho de que la aritmética módulo dos forma un cuerpo finito . Dado que a XOR b XOR c se evalúa como VERDADERO si y solo si exactamente 1 o 3 miembros de { a , b , c } son VERDADEROS, cada solución del problema 1 en 3-SAT para una fórmula CNF dada también es una solución del problema XOR-3-SAT, y a su vez cada solución de XOR-3-SAT es una solución de 3-SAT; vea la imagen. Como consecuencia, para cada fórmula CNF, es posible resolver el problema XOR-3-SAT definido por la fórmula y, con base en el resultado, inferir que el problema 3-SAT es solucionable o que el problema 1-en-3-SAT es irresoluble.

Siempre que las clases de complejidad P y NP no sean iguales , ni la satisfacibilidad 2-, ni la satisfacibilidad de Horn, ni la satisfacibilidad XOR son NP-completas, a diferencia de SAT.

Teorema de dicotomía de Schaefer

Las restricciones anteriores (CNF, 2CNF, 3CNF, Horn, XOR-SAT) limitan las fórmulas consideradas a ser conjunciones de subfórmulas; cada restricción establece una forma específica para todas las subfórmulas: por ejemplo, solo las cláusulas binarias pueden ser subfórmulas en 2CNF.

El teorema de dicotomía de Schaefer establece que, para cualquier restricción a las funciones booleanas que se pueden utilizar para formar estas subfórmulas, el problema de satisfacibilidad correspondiente está en P o es NP-completo. La pertenencia a P de la satisfacibilidad de las fórmulas 2CNF, Horn y XOR-SAT son casos especiales de este teorema. [14]

La siguiente tabla resume algunas variantes comunes del SAT.

Extensiones del SAT

Una extensión que ha ganado popularidad significativa desde 2003 son las teorías de módulo de satisfacibilidad ( SMT ) que pueden enriquecer las fórmulas CNF con restricciones lineales, matrices, restricciones totalmente diferentes, funciones no interpretadas , [19] etc. Dichas extensiones generalmente permanecen NP-completas, pero ahora hay disponibles solucionadores muy eficientes que pueden manejar muchos de esos tipos de restricciones.

El problema de satisfacibilidad se vuelve más difícil si se permite que tanto los cuantificadores "para todos" ( ∀ ) como "existe" ( ∃ ) vinculen las variables booleanas. Un ejemplo de tal expresión sería ∀ x ∀ y ∃ z ( x ∨ y ∨ z ) ∧ (¬ x ∨ ¬ y ∨ ¬ z ) ; es válida, ya que para todos los valores de x e y , se puede encontrar un valor apropiado de z , es decir, z = VERDADERO si tanto x como y son FALSAS, y z = FALSO en caso contrario. El propio SAT utiliza (tácitamente) solo cuantificadores ∃ . Si solo se permiten cuantificadores ∀ en su lugar, se obtiene el llamado problema de tautología , que es co-NP-completo . Si se permiten ambos cuantificadores, el problema se denomina problema de fórmula booleana cuantificada ( QBF ), que se puede demostrar que es PSPACE-completo . Se cree ampliamente que los problemas PSPACE-completos son estrictamente más difíciles que cualquier problema en NP, aunque esto aún no se ha demostrado. Usando sistemas P altamente paralelos , los problemas QBF-SAT se pueden resolver en tiempo lineal. [20]

La prueba SAT ordinaria pregunta si existe al menos una asignación de variable que haga que la fórmula sea verdadera. Existen diversas variantes que se ocupan de la cantidad de dichas asignaciones:

Otras generalizaciones incluyen la satisfacibilidad de la lógica de primer y segundo orden , problemas de satisfacción de restricciones y programación de enteros 0-1 .

Encontrar una tarea satisfactoria

Mientras que SAT es un problema de decisión , el problema de búsqueda de una asignación satisfactoria se reduce a SAT. Es decir, cada algoritmo que responde correctamente si una instancia de SAT es solucionable se puede utilizar para encontrar una asignación satisfactoria. Primero, la pregunta se hace sobre la fórmula dada Φ. Si la respuesta es "no", la fórmula es insatisfacible. De lo contrario, la pregunta se hace sobre la fórmula parcialmente instanciada Φ { x 1 = VERDADERO} , es decir, Φ con la primera variable x 1 reemplazada por VERDADERO, y simplificada en consecuencia. Si la respuesta es "sí", entonces x 1 = VERDADERO, de lo contrario x 1 = FALSO. Los valores de otras variables se pueden encontrar posteriormente de la misma manera. En total, se requieren n +1 ejecuciones del algoritmo, donde n es el número de variables distintas en Φ.

Esta propiedad se utiliza en varios teoremas de la teoría de la complejidad:

NP ⊆ P/poly ⇒ PH = Σ 2   ( teorema de Karp-Lipton )
NP ⊆ BPP ⇒ NP = RP
P = NP ⇒ FP = FNP

Algoritmos para resolver el SAT

Dado que el problema SAT es NP-completo, solo se conocen algoritmos con complejidad exponencial en el peor de los casos. A pesar de esto, durante la década de 2000 se desarrollaron algoritmos eficientes y escalables para SAT y han contribuido a avances dramáticos en la capacidad de resolver automáticamente instancias de problemas que involucran decenas de miles de variables y millones de restricciones (es decir, cláusulas). [1] Los ejemplos de tales problemas en la automatización del diseño electrónico (EDA) incluyen la verificación de equivalencia formal , la verificación de modelos , la verificación formal de microprocesadores canalizados , [19] la generación automática de patrones de prueba , el enrutamiento de FPGA , [26] los problemas de planificación y programación , etc. Un motor de resolución de SAT también se considera un componente esencial en la caja de herramientas de automatización del diseño electrónico .

Las principales técnicas utilizadas por los solucionadores SAT modernos incluyen el algoritmo Davis–Putnam–Logemann–Loveland (o DPLL), el aprendizaje de cláusulas impulsado por conflictos (CDCL) y algoritmos de búsqueda local estocástica como WalkSAT . Casi todos los solucionadores SAT incluyen tiempos de espera, por lo que terminarán en un tiempo razonable incluso si no pueden encontrar una solución. Diferentes solucionadores SAT encontrarán diferentes instancias fáciles o difíciles, y algunos se destacan en demostrar la insatisfacción, y otros en encontrar soluciones. Recientemente [ ¿cuándo? ] se han realizado intentos para aprender la satisfacibilidad de una instancia utilizando técnicas de aprendizaje profundo. [27]

Los solucionadores SAT se desarrollan y comparan en concursos de resolución SAT. [28] Los solucionadores SAT modernos también están teniendo un impacto significativo en los campos de verificación de software, resolución de restricciones en inteligencia artificial e investigación de operaciones, entre otros.

Véase también

Notas

  1. ^ El problema SAT para fórmulas arbitrarias también es NP-completo, ya que se demuestra fácilmente que está en NP, y no puede ser más fácil que SAT para fórmulas CNF.
  2. ^ es decir, al menos tan difícil como cualquier otro problema en NP. Un problema de decisión es NP-completo si y solo si está en NP y es NP-completo.
  3. ^ es decir, tal que un literal no es la negación del otro
  4. ^ a saber, todos los maxterms que se pueden construir con d 1 ,⋯, d k , excepto d 1 ∨⋯∨ d k
  5. ^ Formalmente, se emplean formas normales conjuntivas generalizadas con una función booleana ternaria R , que es VERDADERA solo si 1 o 3 de sus argumentos lo son. Una cláusula de entrada con más de 3 literales se puede transformar en una conjunción equisatisfacible de cláusulas de 3 literales similar a la anterior; es decir, XOR-SAT se puede reducir a XOR-3-SAT.

Enlaces externos

Wikimedia Commons tiene medios relacionados con Problema de satisfacibilidad booleana .

Referencias

  1. ^ ab Ohrimenko, Olga; Stuckey, Peter J.; Codish, Michael (2007), "Propagación = Generación de cláusulas perezosas", Principles and Practice of Constraint Programming – CP 2007 , Lecture Notes in Computer Science, vol. 4741, págs. 544–558, CiteSeerX  10.1.1.70.5471 , doi :10.1007/978-3-540-74970-7_39, ISBN 978-3-540-74969-1Los solucionadores SAT modernos a menudo pueden manejar problemas con millones de restricciones y cientos de miles de variables..
  2. ^ Hong, Ted; Li, Yanjing; Park, Sung-Boem; Mui, Diana; Lin, David; Kaleq, Ziyad Abdel; Hakim, Nagib; Naeimi, Helia; Gardner, Donald S.; Mitra, Subhasish (noviembre de 2010). "QED: pruebas de detección rápida de errores para una validación posterior al silicio efectiva". Conferencia internacional de pruebas IEEE de 2010. págs. 1–10. doi :10.1109/TEST.2010.5699215. ISBN. 978-1-4244-7206-2.S2CID 7909084  .
  3. ^ Karp, Richard M. (1972). "Reducibilidad entre problemas combinatorios" (PDF) . En Raymond E. Miller; James W. Thatcher (eds.). Complejidad de los cálculos informáticos . Nueva York: Plenum. págs. 85-103. ISBN. 0-306-30707-3Archivado desde el original (PDF) el 29 de junio de 2011. Consultado el 7 de mayo de 2020 .Aquí: p.86
  4. ^ Aho, Alfred V.; Hopcroft, John E.; Ullman, Jeffrey D. (1974). El diseño y análisis de algoritmos informáticos . Addison-Wesley. pág. 403. ISBN 0-201-00029-6.
  5. ^ Massacci, Fabio; Marraro, Laura (1 de febrero de 2000). "Criptoanálisis lógico como problema SAT". Revista de razonamiento automatizado . 24 (1): 165–203. doi :10.1023/A:1006326723002. S2CID  3114247.
  6. ^ Mironov, Ilya; Zhang, Lintao (2006). "Aplicaciones de los solucionadores SAT al criptoanálisis de funciones hash". En Biere, Armin; Gomes, Carla P. (eds.). Teoría y aplicaciones de las pruebas de satisfacibilidad - SAT 2006. Apuntes de clase en informática. Vol. 4121. Springer. págs. 102–115. doi :10.1007/11814948_13. ISBN 978-3-540-37207-3.
  7. ^ Vizel, Y.; Weissenbacher, G.; Malik, S. (2015). "Solucionadores de satisfacibilidad booleana y sus aplicaciones en la verificación de modelos". Actas del IEEE . 103 (11): 2021–2035. doi :10.1109/JPROC.2015.2455034. S2CID  10190144.
  8. ^ Cook, Stephen A. (1971). "La complejidad de los procedimientos de demostración de teoremas" (PDF) . Actas del tercer simposio anual de la ACM sobre teoría de la computación - STOC '71 . págs. 151-158. CiteSeerX 10.1.1.406.395 . doi :10.1145/800157.805047. S2CID  7573663. Archivado (PDF) desde el original el 9 de octubre de 2022. 
  9. ^ Levin, Leonid (1973). "Problemas de búsqueda universal (ruso: Универсальные задачи перебора, Universal'nye perebornye zadachi)". Problemas de transmisión de información (ruso: Проблемы передачи информа́ции, Problemy Peredachi Informatsii) . 9 (3): 115-116.(pdf) (en ruso) , traducido al inglés por Trakhtenbrot, BA (1984). "Un estudio de los enfoques rusos de los algoritmos perebor (búsquedas de fuerza bruta)". Anales de la historia de la informática . 6 (4): 384–400. doi :10.1109/MAHC.1984.10036. S2CID  950581.
  10. ^ Aho, Hopcroft y Ullman (1974), Teorema 10.4.
  11. ^ Aho, Hopcroft y Ullman (1974), Teorema 10.5.
  12. ^ Schöning, Uwe (octubre de 1999). "Un algoritmo probabilístico para k-SAT y problemas de satisfacción de restricciones" (PDF) . 40.º Simposio anual sobre fundamentos de la informática (Cat. N.º 99CB37039) . pp. 410–414. doi :10.1109/SFFCS.1999.814612. ISBN. 0-7695-0409-4. S2CID  123177576. Archivado (PDF) del original el 9 de octubre de 2022.
  13. ^ Selman, Bart; Mitchell, David; Levesque, Hector (1996). "Generación de problemas de satisfacibilidad difíciles". Inteligencia artificial . 81 (1–2): 17–29. CiteSeerX 10.1.1.37.7362 . doi :10.1016/0004-3702(95)00045-3. 
  14. ^ abc Schaefer, Thomas J. (1978). "La complejidad de los problemas de satisfacibilidad" (PDF) . Actas del 10º Simposio Anual de la ACM sobre Teoría de la Computación . San Diego, California. págs. 216–226. CiteSeerX 10.1.1.393.8951 . doi :10.1145/800133.804350. 
  15. ^ Schaefer (1978), pág. 222, Lema 3.5.
  16. ^ Arkin, Esther M.; Banik, Aritra; Carmi, Paz; Citovsky, Gui; Katz, Matthew J.; Mitchell, Joseph SB; Simakov, Marina (11 de diciembre de 2018). "Selección y cobertura de puntos coloreados". Matemáticas Aplicadas Discretas . 250 : 75–86. doi : 10.1016/j.dam.2018.05.011 . ISSN  0166-218X.
  17. ^ Buning, HK; Karpinski, Marek; Flogel, A. (1995). "Resolución para fórmulas booleanas cuantificadas". Información y computación . 117 (1). Elsevier: 12–18. doi : 10.1006/inco.1995.1025 .
  18. ^ Moore, Cristopher ; Mertens, Stephan (2011), La naturaleza de la computación, Oxford University Press, pág. 366, ISBN 9780199233212.
  19. ^ ab RE Bryant, SM German y MN Velev, Verificación de microprocesadores utilizando procedimientos de decisión eficientes para una lógica de igualdad con funciones no interpretadas, en Tablas analíticas y métodos relacionados, págs. 1–13, 1999.
  20. ^ Alhazov, Artiom; Martín-Vide, Carlos; Pan, Linqiang (2003). "Resolución de un problema PSPACE-completo mediante el reconocimiento de sistemas P con membranas activas restringidas". Fundamenta Informaticae . 58 : 67–77.Aquí: Sec.3, Teoría 3.1
  21. ^ Blass, Andreas; Gurevich, Yuri (1982-10-01). "Sobre el problema de la satisfacibilidad única". Información y Control . 55 (1): 80–88. doi : 10.1016/S0019-9958(82)90439-9 . hdl : 2027.42/23842 . ISSN  0019-9958.
  22. ^ "Complexity Zoo:U - Complexity Zoo". complexzoo.uwaterloo.ca . Archivado desde el original el 2019-07-09 . Consultado el 2019-12-05 .
  23. ^ Kozen, Dexter C. (2006). "Conferencia complementaria F: Satisfacción única". Teoría de la computación . Textos en informática. Springer. pág. 180. ISBN 9781846282973.
  24. ^ Valiant, L.; Vazirani, V. (1986). "NP es tan fácil como detectar soluciones únicas" (PDF) . Theoretical Computer Science . 47 : 85–93. doi : 10.1016/0304-3975(86)90135-0 .
  25. ^ Buldas, Ahto; Lenin, Aleksandr; Willemson, Jan; Charnamord, Anton (2017). "Certificados de inviabilidad simples para árboles de ataque". En Obana, Satoshi; Chida, Koji (eds.). Avances en seguridad informática y de la información . Apuntes de clase en informática. Vol. 10418. Springer International Publishing. págs. 39–55. doi :10.1007/978-3-319-64200-0_3. ISBN 9783319642000.
  26. ^ Gi-Joon Nam; Sakallah, KA; Rutenbar, RA (2002). "Un nuevo enfoque de enrutamiento detallado de FPGA a través de satisfacibilidad booleana basada en búsqueda" (PDF) . IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems . 21 (6): 674. doi :10.1109/TCAD.2002.1004311. Archivado desde el original (PDF) el 2016-03-15 . Consultado el 2015-09-04 .
  27. ^ Selsam, Daniel; Lamm, Matthew; Bünz, Benedikt; Liang, Percy; de Moura, Leonardo; Dill, David L. (11 de marzo de 2019). "Aprendizaje de un solucionador SAT a partir de la supervisión de un solo bit". arXiv : 1802.03685 [cs.AI].
  28. ^ "La página web de las competiciones internacionales SAT" . Consultado el 15 de noviembre de 2007 .

Fuentes

Lectura adicional

(por fecha de publicación)