
La generación de malla es la práctica de crear una malla , una subdivisión de un espacio geométrico continuo en celdas geométricas y topológicas discretas. A menudo estas células forman un complejo simple . Normalmente las celdas dividen el dominio de entrada geométrico. Las celdas de malla se utilizan como aproximaciones locales discretas del dominio más grande. Las mallas se crean mediante algoritmos informáticos, a menudo con guía humana a través de una GUI , según la complejidad del dominio y el tipo de malla deseada. Un objetivo típico es crear una malla que capture con precisión la geometría del dominio de entrada, con celdas de alta calidad (bien formadas) y sin tantas celdas que hagan que los cálculos posteriores sean intratables. La malla también debe ser fina (tener pequeños elementos) en las zonas que sean importantes para los cálculos posteriores.
Las mallas se utilizan para renderizar en la pantalla de una computadora y para simulaciones físicas, como análisis de elementos finitos o dinámica de fluidos computacional . Las mallas se componen de celdas simples como triángulos porque, por ejemplo, sabemos cómo realizar operaciones como cálculos de elementos finitos (ingeniería) o trazado de rayos (gráficos por computadora) en triángulos, pero no sabemos cómo realizar estas operaciones directamente en espacios complicados. y formas como un puente de carretera. Podemos simular la resistencia del puente, o dibujarlo en la pantalla de una computadora, realizando cálculos en cada triángulo y calculando las interacciones entre triángulos.
Una distinción importante es entre mallado estructurado y no estructurado. En el mallado estructurado, la malla es una red regular, como una matriz, con conectividad implícita entre elementos. En el mallado no estructurado, los elementos se pueden conectar entre sí en patrones irregulares y se pueden capturar dominios más complicados. Esta página trata principalmente sobre mallas no estructuradas. Si bien una malla puede ser una triangulación , el proceso de mallado se distingue de la triangulación de conjuntos de puntos en que el mallado incluye la libertad de agregar vértices que no están presentes en la entrada. "Facetar" (triangular) los modelos CAD para dibujo tiene la misma libertad para agregar vértices, pero el objetivo es representar la forma con precisión utilizando la menor cantidad de triángulos posible y la forma de los triángulos individuales no es importante. En su lugar, las representaciones gráficas por computadora de texturas y condiciones de iluminación realistas utilizan mallas.
Muchos programas de generación de mallas están acoplados a un sistema CAD que define su entrada y a un software de simulación para tomar su salida. La entrada puede variar mucho, pero las formas más comunes son el modelado sólido , el modelado geométrico , NURBS , B-rep , STL o una nube de puntos .
Los términos " generación de malla", " generación de malla ", " mallado " y " mallado " suelen usarse indistintamente, aunque estrictamente hablando los dos últimos son más amplios y abarcan la mejora de la malla: cambiar la malla con el objetivo de aumentar la velocidad. o precisión de los cálculos numéricos que se realizarán sobre ella. En la representación de gráficos por computadora y en matemáticas , una malla a veces se denomina teselación .
Las caras de la malla (celdas, entidades) tienen diferentes nombres según su dimensión y el contexto en el que se utilizará la malla. En elementos finitos, las entidades de malla de mayor dimensión se denominan "elementos", los "bordes" son 1D y los "nodos" son 0D. Si los elementos son 3D, entonces las entidades 2D son "caras". En geometría computacional, los puntos 0D se denominan vértices. Los tetraedros suelen abreviarse como "tets"; los triángulos son "tris", los cuadriláteros son "quads" y los hexaedros (cubos topológicos) son "hexaedros".
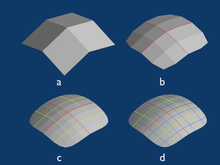

Muchas técnicas de mallado se basan en los principios de la triangulación de Delaunay , junto con reglas para sumar vértices, como el algoritmo de Ruppert . Una característica distintiva es que inicialmente se forma una malla gruesa de todo el espacio, luego se agregan vértices y triángulos. Por el contrario, los algoritmos frontales avanzados comienzan desde el límite del dominio y agregan elementos que llenan gradualmente el interior. Las técnicas híbridas hacen ambas cosas. Una clase especial de técnicas de frente de avance crea finas capas límite de elementos para el flujo de fluidos. En la generación de malla estructurada, toda la malla es un gráfico de celosía , como una cuadrícula regular de cuadrados. En el mallado estructurado en bloques, el dominio se divide en grandes subregiones, cada una de las cuales es una malla estructurada. Algunos métodos directos comienzan con una malla estructurada en bloques y luego mueven la malla para ajustarse a la entrada; consulte Generación automática de malla hexagonal basada en polycube . Otro método directo consiste en cortar las celdas estructuradas por el límite del dominio; ver escultura basada en cubos de marcha .
Algunos tipos de mallas son mucho más difíciles de crear que otros. Las mallas simples tienden a ser más fáciles que las cúbicas. Una categoría importante es la generación de una malla hexagonal que se ajusta a una malla de superficie cuádruple fija; una subárea de investigación estudia la existencia y generación de mallas de configuraciones pequeñas específicas, como el trapezoedro tetragonal . Debido a la dificultad de este problema, la existencia de mallas combinatorias hexagonales se ha estudiado aparte del problema de generar buenas realizaciones geométricas. Si bien los algoritmos conocidos generan mallas simples con una calidad mínima garantizada, tales garantías son raras para las mallas cúbicas y muchas implementaciones populares generan hexágonos invertidos (de adentro hacia afuera) a partir de algunas entradas.
Las mallas a menudo se crean en serie en estaciones de trabajo, incluso cuando los cálculos posteriores sobre la malla se realizarán en paralelo en supercomputadoras. Esto se debe a la limitación de que la mayoría de los generadores de malla son interactivos y a que el tiempo de ejecución de la generación de malla suele ser insignificante en comparación con el tiempo del solucionador. Sin embargo, si la malla es demasiado grande para caber en la memoria de una sola máquina en serie, o si la malla debe cambiarse (adaptarse) durante la simulación, el mallado se realiza en paralelo.

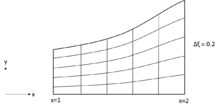
La generación de grillas por métodos algebraicos se basa en la función de interpolación matemática . Se realiza utilizando funciones conocidas en una, dos o tres dimensiones tomando regiones de formas arbitrarias. Es posible que el dominio computacional no sea rectangular, pero por razones de simplicidad, se considera que el dominio es rectangular. La principal ventaja de estos métodos es que proporcionan un control explícito de la forma y el espaciado de la cuadrícula física. El procedimiento más simple que se puede utilizar para producir una malla computacional ajustada a los límites es la transformación de normalización. [1]
Para una boquilla, con la función de descripción, la cuadrícula se puede generar fácilmente usando una división uniforme en la dirección y con incrementos igualmente espaciados en la dirección x , que se describen por
donde denota la coordenada y de la pared de la boquilla. Para valores dados de ( , ), los valores de ( , ) se pueden recuperar fácilmente.
Al igual que los métodos algebraicos, los métodos de ecuaciones diferenciales también se utilizan para generar cuadrículas. La ventaja de utilizar las ecuaciones diferenciales parciales (PDE) es que la solución de las ecuaciones generadoras de la red se puede explotar para generar la malla. La construcción de la cuadrícula se puede realizar utilizando las tres clases de ecuaciones diferenciales parciales .
Las PDE elípticas generalmente tienen soluciones muy suaves que conducen a contornos suaves. Utilizando su suavidad como ventaja, las ecuaciones de Laplace se pueden utilizar preferiblemente porque se descubrió que el jacobiano es positivo como resultado del principio de máximo para funciones armónicas . Después de un extenso trabajo realizado por Crowley (1962) y Winslow (1966) [2] sobre PDE transformando el dominio físico en un plano computacional mientras se mapeaba usando la ecuación de Poisson , Thompson et al. (1974) [3] han trabajado extensamente en PDE elípticas para generar redes. En los generadores de cuadrícula de Poisson, el mapeo se logra marcando los puntos de cuadrícula deseados en el límite del dominio físico, con la distribución de puntos interiores determinada mediante la solución de las ecuaciones escritas a continuación.
donde, son las coordenadas en el dominio computacional, mientras que P y Q son responsables del espaciado de puntos dentro de D. La transformación de las ecuaciones anteriores en el espacio computacional produce un conjunto de dos PDE elípticas de la forma,
dónde
Estos sistemas de ecuaciones se resuelven en el plano computacional en una cuadrícula uniformemente espaciada que nos proporciona las coordenadas de cada punto en el espacio físico. La ventaja de utilizar PDE elípticas es que la solución vinculada a ellas es suave y la cuadrícula resultante es suave. Pero la especificación de P y Q se convierte en una tarea difícil, lo que se suma a sus desventajas. Además, la cuadrícula debe calcularse después de cada paso de tiempo, lo que suma el tiempo de cálculo. [4]
Este esquema de generación de grillas es generalmente aplicable a problemas con dominios abiertos consistentes con el tipo de PDE que describe el problema físico. La ventaja asociada con las PDE hiperbólicas es que las ecuaciones gobernantes deben resolverse solo una vez para generar la red. La distribución de puntos inicial junto con las condiciones de contorno aproximadas forman la entrada requerida y luego la solución avanza hacia afuera. Steger y Sorenson (1980) [5] propusieron un método de ortogonalidad de volumen que utiliza PDE hiperbólicas para la generación de mallas. Para un problema 2-D, considerando que el espacio computacional está dado por , el inverso del jacobiano está dado por,
donde representa el área en el espacio físico para un área determinada en el espacio computacional. La segunda ecuación vincula la ortogonalidad de las líneas de la cuadrícula en el límite del espacio físico que se puede escribir como
Para que las superficies y sean perpendiculares la ecuación se convierte en
El problema asociado con dicho sistema de ecuaciones es la especificación de . Una mala selección de puede provocar shock y propagación discontinua de esta información por toda la malla. Si bien la malla es ortogonal se genera muy rápidamente, lo que resulta una ventaja con este método.
La técnica de resolución es similar a la de las PDE hiperbólicas: avanza la solución alejándola de la superficie de datos inicial y satisface las condiciones de contorno al final. Nakamura (1982) y Edwards (1985) desarrollaron las ideas básicas para la generación de redes parabólicas. La idea utiliza la ecuación de Laplace o la de Poisson y trata especialmente las partes que controlan el comportamiento elíptico. Los valores iniciales se dan como las coordenadas del punto a lo largo de la superficie y el avance de las soluciones hacia la superficie exterior del objeto que satisface las condiciones de contorno a lo largo de los bordes.
El control de la separación entre rejillas no se ha propuesto hasta ahora. Nakamura y Edwards, el control de la red se logró utilizando un espaciado no uniforme. La generación de red parabólica muestra una ventaja sobre la generación de red hiperbólica: no se producen choques ni discontinuidades y la red es relativamente suave. Sin embargo, las especificaciones de los valores iniciales y la selección del tamaño del paso para controlar los puntos de la cuadrícula requieren mucho tiempo, pero estas técnicas pueden ser efectivas cuando se adquiere familiaridad y experiencia.
Este método incluye una técnica que minimiza la suavidad, la ortogonalidad y la variación de volumen de la cuadrícula . Este método forma una plataforma matemática para resolver problemas de generación de redes. En este método, se genera una cuadrícula alternativa mediante una nueva malla después de cada iteración y se calcula la velocidad de la cuadrícula utilizando el método de diferencia hacia atrás. Esta técnica es poderosa con la desventaja de que se requiere esfuerzo para resolver las ecuaciones relacionadas con la cuadrícula. Era necesario realizar más trabajo para minimizar las integrales que reducirán el tiempo de CPU.
La principal importancia de este esquema es que proporciona un método que generará la cuadrícula automáticamente. Con este método, las rejillas se segmentan en bloques según la superficie del elemento y se proporciona una estructura para garantizar una conectividad adecuada. Para interpretar el flujo de datos se utiliza el solucionador. Cuando se emplea un esquema no estructurado, el interés principal es satisfacer la demanda del usuario y se utiliza un generador de red para realizar esta tarea. El almacenamiento de información en un esquema estructurado es de celda a celda en lugar de de cuadrícula a cuadrícula y, por lo tanto, se necesita más espacio de memoria. Debido a la ubicación aleatoria de las celdas, la eficiencia del solucionador en el esquema no estructurado es menor en comparación con el esquema estructurado. [6]
Es necesario tener en cuenta algunos puntos al momento de construir la red . El punto de la cuadrícula con alta resolución crea dificultades tanto para los estructurados como para los no estructurados. Por ejemplo, en el caso de una capa límite , el esquema estructurado produce una rejilla alargada en la dirección del flujo. Por otro lado, las cuadrículas no estructuradas requieren una mayor densidad de celdas en la capa límite porque la celda debe ser lo más equilátera posible para evitar errores. [7]
Debemos identificar qué información se requiere para identificar la celda y todos los vecinos de la celda en la malla computacional . Podemos optar por ubicar los puntos arbitrarios en cualquier lugar que queramos para la cuadrícula no estructurada. Se utiliza un esquema de inserción de puntos para insertar los puntos de forma independiente y se determina la conectividad de la celda. Esto sugiere que el punto se identifique a medida que se insertan. La lógica para establecer una nueva conectividad se determina una vez que se insertan los puntos. Se necesitan datos que formen puntos de cuadrícula que identifiquen la celda de la cuadrícula. A medida que se forma cada celda, se numera y se ordenan los puntos. Además, se necesita la información de la celda vecina.
Un problema al resolver ecuaciones diferenciales parciales utilizando métodos anteriores es que se construye la cuadrícula y los puntos se distribuyen en el dominio físico antes de que se conozcan los detalles de la solución. Por lo tanto, la red puede ser o no la mejor para el problema dado. [8]
Se utilizan métodos adaptativos para mejorar la precisión de las soluciones. El método adaptativo se conoce como método 'h' si se utiliza el refinamiento de la malla, método 'r' si el número de puntos de la cuadrícula es fijo y no redistribuido y 'p' si el orden del esquema de solución aumenta en la teoría de elementos finitos. Los problemas multidimensionales que utilizan el esquema de equidistribución se pueden resolver de varias maneras. Los más sencillos de entender son los generadores de rejilla de Poisson con función de control basada en la equidistribución de la función de peso con la difusión configurada como un múltiplo del volumen celular deseado. El esquema de equidistribución también se puede aplicar al problema no estructurado. El problema es que la conectividad dificulta si el movimiento del punto de malla es muy grande.
El flujo constante y el cálculo del flujo con precisión en el tiempo se pueden resolver mediante este método adaptativo. La cuadrícula se refina y después de un número predeterminado de iteraciones para adaptarla a un problema de flujo estacionario. La cuadrícula dejará de ajustarse a los cambios una vez que la solución converja. Con el tiempo, se requiere un acoplamiento preciso de las ecuaciones diferenciales parciales del problema físico y aquellas que describen el movimiento de la red.
Normalmente las celdas son poligonales o poliédricas y forman una malla que divide el dominio. Las clases importantes de elementos bidimensionales incluyen triángulos (símplices) y cuadriláteros (cuadrados topológicos). En tres dimensiones, las celdas más comunes son los tetraedros (símplices) y los hexaedros (cubos topológicos). Las mallas simples pueden ser de cualquier dimensión e incluir triángulos (2D) y tetraedros (3D) como instancias importantes. Las mallas cúbicas son la categoría pandimensional que incluye quads (2D) y hexágonos (3D). En 3D, las pirámides de 4 lados y los prismas de 3 lados aparecen en mallas conformes de tipo celular mixto.
La malla está incrustada en un espacio geométrico que suele ser bidimensional o tridimensional , aunque en ocasiones la dimensión se incrementa en uno añadiendo la dimensión temporal. Las mallas de mayores dimensiones se utilizan en contextos especializados. Las mallas unidimensionales también son útiles. Una categoría importante son las mallas de superficie, que son mallas 2D incrustadas en 3D para representar una superficie curva.
Los gráficos duales tienen varias funciones en el mallado. Se puede hacer una malla de diagrama de Voronoi poliédrico dualizando una malla simplicial de triangulación de Delaunay . Se puede crear una malla cúbica generando una disposición de superficies y dualizando el gráfico de intersección; ver continuo de giro espacial . A veces, tanto la malla primaria como su malla dual se utilizan en la misma simulación; ver operador estrella de Hodge . Esto surge de la física que involucra operadores de divergencia y curvatura (matemáticos) , como flujo y vorticidad o electricidad y magnetismo , donde una variable vive naturalmente en las caras primarias y su contraparte en las caras duales.
Las mallas tridimensionales creadas para el análisis de elementos finitos deben consistir en tetraedros , pirámides , prismas o hexaedros . Los utilizados para el método de los volúmenes finitos pueden consistir en poliedros arbitrarios . Los utilizados para los métodos de diferencias finitas consisten en matrices estructuradas por partes de hexaedros conocidas como mallas estructuradas de bloques múltiples. Las pirámides de 4 lados son útiles para conectar conformemente hexágonos a tets. Los prismas de 3 lados se utilizan para capas límite que se ajustan a una malla tet del interior lejano del objeto.
Las mallas de superficie son útiles en gráficos por computadora donde las superficies de los objetos reflejan la luz (también la dispersión del subsuelo ) y no se necesita una malla 3D completa. Las mallas de superficie también se utilizan para modelar objetos delgados como láminas de metal en la fabricación de automóviles y exteriores de edificios en arquitectura. Las mallas cúbicas de alta dimensión (p. ej., 17) son comunes en astrofísica y teoría de cuerdas .
¿Cuál es la definición precisa de malla? No existe una descripción matemática universalmente aceptada que se aplique en todos los contextos. Sin embargo, algunos objetos matemáticos son claramente mallas: un complejo simplicial es una malla compuesta de simples. La mayoría de las mallas poliédricas (por ejemplo, cúbicas) son conformes, lo que significa que tienen la estructura celular de un complejo CW , una generalización de un complejo simplicial . Una malla no tiene por qué ser simple porque un subconjunto arbitrario de nodos de una celda no es necesariamente una celda: por ejemplo, tres nodos de un cuadrilátero no definen una celda. Sin embargo, dos celdas se cruzan en las celdas: por ejemplo, un quad no tiene un nodo en su interior. La intersección de dos celdas puede ser de varias celdas: por ejemplo, dos quads pueden compartir dos bordes. A veces está prohibido y rara vez se desea que una intersección tenga más de una celda; El objetivo de algunas técnicas de mejora de la malla (por ejemplo, el acolchado) es eliminar estas configuraciones. En algunos contextos, se hace una distinción entre una malla topológica y una malla geométrica cuya incrustación satisface ciertos criterios de calidad.
Las variantes de malla importantes que no son complejos CW incluyen mallas no conformes donde las células no se encuentran estrictamente cara a cara, pero, no obstante, dividen el dominio. Un ejemplo de esto es un octree , donde la cara de un elemento puede dividirse por las caras de elementos adyacentes. Estas mallas son útiles para simulaciones basadas en flujos. En las cuadrículas desbordadas, hay múltiples mallas conformes que se superponen geométricamente y no dividen el dominio; consulte, por ejemplo, Desbordamiento, el solucionador de FLUJO de cuadrícula OVERset . Los métodos llamados sin malla o sin malla a menudo hacen uso de alguna discretización del dominio similar a una malla y tienen funciones básicas con soporte superpuesto. A veces se crea una malla local cerca de cada punto de grado de libertad de la simulación, y estas mallas pueden superponerse y no ser conformes entre sí.
Las triangulaciones implícitas se basan en un complejo delta: para cada triángulo, las longitudes de sus aristas y un mapa de pegado entre las aristas de la cara. (por favor ampliar)
Muchas mallas utilizan elementos lineales, donde el mapeo del elemento abstracto al elemento realizado es lineal y los bordes de la malla son segmentos rectos. Las asignaciones de polinomios de orden superior son comunes, especialmente las cuadráticas. Un objetivo principal de los elementos de orden superior es representar con mayor precisión el límite del dominio, aunque también tienen ventajas de precisión en el interior de la malla. Una de las motivaciones para las mallas cúbicas es que los elementos cúbicos lineales tienen algunas de las mismas ventajas numéricas que los elementos cuadráticos simpliciales. En la técnica de simulación de análisis isogeométrico , las celdas de malla que contienen el límite del dominio utilizan la representación CAD directamente en lugar de una aproximación lineal o polinómica.
Mejorar una malla implica cambiar su conectividad discreta, la posición geométrica continua de sus celdas o ambas. Para cambios discretos, para elementos simples se intercambian bordes e se insertan/eliminan nodos. Se realizan los mismos tipos de operaciones para mallas cúbicas (quad/hex), aunque hay menos operaciones posibles y los cambios locales tienen consecuencias globales. Por ejemplo, para una malla hexaédrica, fusionar dos nodos crea celdas que no son hexágonos, pero si se fusionan nodos diagonalmente opuestos en un cuadrilátero y esto se propaga hasta colapsar toda una columna de hexágonos conectados por caras, entonces todas las celdas restantes seguirán siendo hexágonos. En el refinamiento de malla adaptativo , los elementos se dividen (refinamiento h) en áreas donde la función que se calcula tiene un gradiente alto. Las mallas también se engrosan, eliminando elementos para mayor eficiencia. El método multigrid hace algo similar al refinamiento y el engrosamiento para acelerar la resolución numérica, pero sin cambiar realmente la malla.
Para cambios continuos, los nodos se mueven o las caras de dimensiones superiores se mueven cambiando el orden polinómico de los elementos. Mover nodos para mejorar la calidad se llama "suavizado" o "r-refinamiento" y aumentar el orden de los elementos se llama "p-refinamiento". Los nodos también se mueven en simulaciones donde la forma de los objetos cambia con el tiempo. Esto degrada la forma de los elementos. Si el objeto se deforma lo suficiente, se vuelve a mallar todo el objeto y la solución actual se asigna de la malla antigua a la nueva.
El campo es altamente interdisciplinario, con contribuciones en matemáticas , informática e ingeniería . Meshing I+D se distingue por un enfoque igual en matemáticas y computación discreta y continua, como ocurre con la geometría computacional , pero en contraste con la teoría de grafos (discreta) y el análisis numérico (continuo). La generación de mallas es engañosamente difícil: es fácil para los humanos ver cómo crear una malla de un objeto determinado, pero es difícil programar una computadora para que tome buenas decisiones para entradas arbitrarias a priori. Existe una infinita variedad de geometría que se encuentra en la naturaleza y en los objetos creados por el hombre. Muchos investigadores de generación de mallas fueron los primeros usuarios de mallas. La generación de mallas continúa recibiendo atención, apoyo y financiación generalizados porque el tiempo humano para crear una malla eclipsa el tiempo para configurar y resolver el cálculo una vez que la malla está terminada. Esta ha sido siempre la situación desde que se inventaron la simulación numérica y los gráficos por computadora, porque a medida que el hardware de las computadoras y el software de resolución de ecuaciones simples mejoraron, la gente se sintió atraída por modelos geométricos más grandes y complejos en un intento por lograr una mayor fidelidad, conocimiento científico y expresión artística.
La investigación sobre mallado se publica en una amplia gama de revistas. Esto está en consonancia con el carácter interdisciplinario de la investigación necesaria para avanzar, y también con la amplia variedad de aplicaciones que utilizan las mallas. Cada año aparecen alrededor de 150 publicaciones en malla en 20 revistas, y como máximo 20 publicaciones aparecen en una sola revista. No existe ninguna revista cuyo tema principal sea el entrelazamiento. En negrita se encuentran las revistas que publican al menos 10 artículos sobre mallados por año .
(Las conferencias cuyo tema principal es el mallado están en negrita ) .
Los talleres cuyo tema principal es el entrelazado están en negrita.
Muchas descripciones de productos comerciales enfatizan la simulación en lugar de la tecnología de malla que permite la simulación.
Estas herramientas generan las mallas particionadas necesarias para el modelado de elementos finitos de múltiples materiales.
Modelos (entradas) y mallas (salidas) útiles para comparar algoritmos de mallado y mallas.
Motores de modelado vinculados con software de generación de mallas para representar la geometría del dominio.
Formatos de archivos (de salida) comunes para describir mallas.