Péndulo invertido

Péndulo con centro de masa sobre el pivote

Carro de equilibrio, un sistema robótico simple alrededor de 1976. El carro contiene un sistema servo que monitorea el ángulo de la varilla y mueve el carro hacia adelante y hacia atrás para mantenerlo en posición vertical.

Un péndulo invertido es un péndulo que tiene su centro de masa por encima de su punto de pivote . Es inestable y se cae sin ayuda adicional. Se puede suspender de forma estable en esta posición invertida utilizando un sistema de control para monitorear el ángulo del poste y mover el punto de pivote horizontalmente de nuevo debajo del centro de masa cuando comienza a caer, manteniéndolo equilibrado. El péndulo invertido es un problema clásico en dinámica y teoría de control y se utiliza como punto de referencia para probar estrategias de control. A menudo se implementa con el punto de pivote montado en un carro que puede moverse horizontalmente bajo el control de un sistema servo electrónico como se muestra en la foto; esto se llama aparato de carro y poste . ^[1] La mayoría de las aplicaciones limitan el péndulo a 1 grado de libertad fijando el poste a un eje de rotación . Mientras que un péndulo normal es estable cuando cuelga hacia abajo, un péndulo invertido es inherentemente inestable y debe equilibrarse activamente para permanecer en posición vertical; Esto se puede hacer aplicando un par en el punto de pivote, moviendo el punto de pivote horizontalmente como parte de un sistema de retroalimentación , cambiando la velocidad de rotación de una masa montada en el péndulo sobre un eje paralelo al eje de pivote y generando así un par neto en el péndulo, o haciendo oscilar el punto de pivote verticalmente. Una demostración sencilla de cómo mover el punto de pivote en un sistema de retroalimentación se logra equilibrando un palo de escoba boca abajo en la punta del dedo.

Un segundo tipo de péndulo invertido es un inclinómetro para estructuras altas, que consiste en un alambre anclado al fondo de la cimentación y unido a un flotador en un estanque de aceite en la parte superior de la estructura que tiene dispositivos para medir el movimiento de la posición neutra del flotador lejos de su posición original.

Descripción general

Un péndulo con su cuerpo colgando directamente debajo del pivote de apoyo se encuentra en un punto de equilibrio estable , donde permanece inmóvil porque no hay torque sobre el péndulo. Si se lo desplaza de esta posición, experimenta un torque restaurador que lo devuelve a la posición de equilibrio. Un péndulo con su cuerpo en posición invertida, apoyado en una varilla rígida directamente sobre el pivote, a 180° de su posición de equilibrio estable, se encuentra en un punto de equilibrio inestable . En este punto, nuevamente no hay torque sobre el péndulo, pero el más mínimo desplazamiento hacia afuera de esta posición provoca un torque gravitacional sobre el péndulo que lo acelera y lo aleja del equilibrio, provocando que se caiga.

Para estabilizar un péndulo en esta posición invertida, se puede utilizar un sistema de control de retroalimentación , que monitorea el ángulo del péndulo y mueve la posición del punto de pivote hacia los lados cuando el péndulo comienza a caer, para mantenerlo equilibrado. El péndulo invertido es un problema clásico en dinámica y teoría de control y se usa ampliamente como punto de referencia para probar algoritmos de control ( controladores PID , representación en espacio de estados , redes neuronales , control difuso , algoritmos genéticos , etc.). Las variaciones de este problema incluyen enlaces múltiples, lo que permite ordenar el movimiento del carro mientras se mantiene el péndulo, y equilibrar el sistema carro-péndulo en un balancín. El péndulo invertido está relacionado con la guía de cohetes o misiles, donde el centro de gravedad se encuentra detrás del centro de arrastre, lo que provoca inestabilidad aerodinámica. ^[2] La comprensión de un problema similar se puede demostrar mediante robótica simple en forma de un carro de equilibrio. Equilibrar una escoba boca abajo en la punta de un dedo es una demostración sencilla, y el problema se resuelve con transportadores personales autoequilibrados como el Segway PT , el hoverboard autoequilibrado y el monociclo autoequilibrado .

Otra forma de estabilizar un péndulo invertido, sin ningún mecanismo de control o retroalimentación, es haciendo oscilar rápidamente el pivote hacia arriba y hacia abajo. Esto se llama péndulo de Kapitza . Si la oscilación es suficientemente fuerte (en términos de aceleración y amplitud), entonces el péndulo invertido puede recuperarse de las perturbaciones de una manera sorprendentemente contraintuitiva. Si el punto de impulso se mueve en un movimiento armónico simple , el movimiento del péndulo se describe mediante la ecuación de Mathieu . ^[3]

Ecuaciones de movimiento

Las ecuaciones de movimiento de los péndulos invertidos dependen de las restricciones que se impongan al movimiento del péndulo. Los péndulos invertidos se pueden crear en varias configuraciones, lo que da como resultado una serie de ecuaciones de movimiento que describen el comportamiento del péndulo.

Punto de pivote estacionario

En una configuración en la que el punto de pivote del péndulo está fijo en el espacio, la ecuación de movimiento es similar a la de un péndulo no invertido . La ecuación de movimiento que se muestra a continuación supone que no hay fricción ni ninguna otra resistencia al movimiento, una varilla rígida sin masa y la restricción al movimiento bidimensional .

${\displaystyle {\ddot {\theta }}-{g \over \ell }\sin \theta =0}$

Donde es la aceleración angular del péndulo, es la gravedad estándar en la superficie de la Tierra, es la longitud del péndulo y es el desplazamiento angular medido desde la posición de equilibrio. ${\displaystyle {\ddot {\theta }}}$ ${\displaystyle g}$ ${\displaystyle \ell }$ ${\displaystyle \theta }$

Cuando se suma a ambos lados, tiene el mismo signo que el término de aceleración angular: ${\displaystyle {\ddot {\theta }}}$

${\displaystyle {\ddot {\theta }}={g \over \ell }\sin \theta }$

De esta manera, el péndulo invertido se aleja acelerando del equilibrio inestable vertical en la dirección en la que se desplazó inicialmente, y la aceleración es inversamente proporcional a la longitud. Los péndulos altos caen más lentamente que los cortos.

Derivación utilizando torque y momento de inercia:

Dibujo esquemático del péndulo invertido sobre un carro. Se considera que la varilla no tiene masa. La masa del carro y la masa puntual en el extremo de la varilla se indican con M y m. La varilla tiene una longitud l.

Se supone que el péndulo consiste en una masa puntual, de masa , fijada al extremo de una varilla rígida sin masa, de longitud , unida a un punto de pivote en el extremo opuesto a la masa puntual. ${\displaystyle m}$ ${\displaystyle \ell }$

El par neto del sistema debe ser igual al momento de inercia multiplicado por la aceleración angular:

${\displaystyle {\boldsymbol {\tau }}_{\mathrm {net} }=I{\ddot {\theta }}}$

El par debido a la gravedad que proporciona el par neto:

${\displaystyle {\boldsymbol {\tau }}_{\mathrm {net} }=mg\ell \sin \theta \,\!}$

¿Dónde está el ángulo medido desde la posición de equilibrio invertida? ${\displaystyle \theta \ }$

La ecuación resultante:

${\displaystyle I{\ddot {\theta }}=mg\ell \sin \theta \,\!}$

El momento de inercia de una masa puntual:

${\displaystyle I=mR^{2}}$

En el caso del péndulo invertido el radio es la longitud de la varilla, . ${\displaystyle \ell }$

Sustituyendo en ${\displaystyle I=m\ell ^{2}}$

${\displaystyle m\ell ^{2}{\ddot {\theta }}=mg\ell \sin \theta \,\!}$

La masa se divide por cada lado y da como resultado: ${\displaystyle \ell ^{2}}$

${\displaystyle {\ddot {\theta }}={g \over \ell }\sin \theta }$

Péndulo invertido sobre un carro

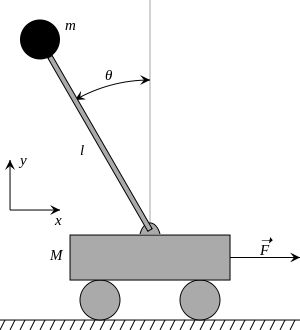
Un péndulo invertido sobre un carro consiste en una masa en la parte superior de un poste de longitud que pivotea sobre una base que se mueve horizontalmente, como se muestra en la imagen adyacente. El carro está restringido al movimiento lineal y está sujeto a fuerzas que provocan o impiden el movimiento. ${\displaystyle m}$ ${\displaystyle \ell }$

Fundamentos de la estabilización

Los aspectos esenciales para estabilizar el péndulo invertido se pueden resumir cualitativamente en tres pasos.

El sencillo sistema de control estabilizador utilizado en el carrito con la copa de vino encima.

1. Si el ángulo de inclinación es hacia la derecha, el carro debe acelerar hacia la derecha y viceversa. ${\displaystyle \theta }$

2. La posición del carro en relación con el centro de la vía se estabiliza modulando ligeramente el ángulo nulo (el error de ángulo que el sistema de control intenta anular) por la posición del carro, es decir, el ángulo nulo donde es pequeño. Esto hace que el poste quiera inclinarse ligeramente hacia el centro de la vía y estabilizarse en el centro de la vía donde el ángulo de inclinación es exactamente vertical. Cualquier desplazamiento en el sensor de inclinación o la pendiente de la vía que de otro modo causaría inestabilidad se traduce en un desplazamiento de posición estable. Un desplazamiento adicional proporciona control de posición. ${\displaystyle x}$ ${\displaystyle =\theta +kx}$ ${\displaystyle k}$

3. Un péndulo normal sujeto a un punto de pivote en movimiento, como una carga levantada por una grúa, tiene una respuesta máxima en la frecuencia en radianes del péndulo de . Para evitar oscilaciones descontroladas, el espectro de frecuencia del movimiento de pivote debe suprimirse cerca de . El péndulo invertido requiere el mismo filtro de supresión para lograr estabilidad. ${\displaystyle \omega _{p}={\sqrt {g/\ell }}}$ ${\displaystyle \omega _{p}}$

Como consecuencia de la estrategia de modulación de ángulo nulo, la retroalimentación de posición es positiva, es decir, una orden repentina de moverse a la derecha produce un movimiento inicial del carro hacia la izquierda seguido de un movimiento a la derecha para reequilibrar el péndulo. La interacción de la inestabilidad del péndulo y la inestabilidad de retroalimentación de posición positiva para producir un sistema estable es una característica que hace que el análisis matemático sea un problema interesante y desafiante.

De las ecuaciones de Lagrange

Las ecuaciones de movimiento se pueden derivar utilizando las ecuaciones de Lagrange . Nos referimos al dibujo de la derecha, donde es el ángulo del péndulo de longitud con respecto a la dirección vertical y las fuerzas que actúan son la gravedad y una fuerza externa F en la dirección x. Definamos como la posición del carro. ${\displaystyle \theta (t)}$ ${\displaystyle l}$ ${\displaystyle x(t)}$

La energía cinética del sistema es: ${\displaystyle T}$

${\displaystyle T={\frac {1}{2}}Mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2},}$

donde es la velocidad del carro y es la velocidad de la masa puntual . y se puede expresar en términos de x y escribiendo la velocidad como la primera derivada de la posición; ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle m}$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle \theta }$

${\displaystyle v_{1}^{2}={\dot {x}}^{2},}$

${\displaystyle v_{2}^{2}=\left({\frac {\rm {d}}{{\rm {d}}t}}{\left(x-\ell \sin \theta \right)}\right)^{2}+\left({\frac {\rm {d}}{{\rm {d}}t}}{\left(\ell \cos \theta \right)}\right)^{2}.}$

Simplificando la expresión obtenemos: ${\displaystyle v_{2}}$

${\displaystyle v_{2}^{2}={\dot {x}}^{2}-2\ell {\dot {x}}{\dot {\theta }}\cos \theta +\ell ^{2}{\dot {\theta }}^{2}.}$

La energía cinética ahora viene dada por:

${\displaystyle T={\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}-m\ell {\dot {x}}{\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}.}$

Las coordenadas generalizadas del sistema son y , cada una tiene una fuerza generalizada. En el eje, la fuerza generalizada se puede calcular a través de su trabajo virtual. ${\displaystyle \theta }$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle Q_{x}}$

${\displaystyle Q_{x}\delta x=F\delta x,\quad Q_{x}=F,}$

En el eje, la fuerza generalizada también se puede calcular a través de su trabajo virtual. ${\displaystyle \theta }$ ${\displaystyle Q_{\theta }}$

${\displaystyle Q_{\theta }\delta \theta =mgl\sin \theta \delta \theta ,\quad Q_{\theta }=mgl\sin \theta .}$

Según las ecuaciones de Lagrange , las ecuaciones de movimiento son:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {T} \over \partial {\dot {x}}}-{\partial {T} \over \partial x}=F,}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\partial {T} \over \partial {\dot {\theta }}}-{\partial {T} \over \partial \theta }=mgl\sin \theta ,}$

Sustituyendo en estas ecuaciones y simplificando obtenemos las ecuaciones que describen el movimiento del péndulo invertido: ${\displaystyle T}$

${\displaystyle \left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F,}$

${\displaystyle \ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta .}$

Estas ecuaciones no son lineales, pero como el objetivo de un sistema de control sería mantener el péndulo en posición vertical, las ecuaciones se pueden linealizar alrededor de . ${\displaystyle \theta \approx 0}$

De las ecuaciones de Euler-Lagrange

Las fuerzas generalizadas pueden escribirse tanto como energía potencial como , ${\displaystyle V_{x}}$ ${\displaystyle V_{\theta }}$

Según el principio de D'Alembert , las fuerzas generalizadas y la energía potencial están conectadas:

${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}}\,,}$

Sin embargo, en determinadas circunstancias, la energía potencial no es accesible y sólo están disponibles fuerzas generalizadas.

Después de obtener el Lagrangiano , también podemos usar la ecuación de Euler-Lagrange para resolver ecuaciones de movimiento: ${\displaystyle L=T-V}$

${\displaystyle {\frac {\partial L}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=0}$,

${\displaystyle {\frac {\partial L}{\partial \theta }}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {\theta }}}}\right)=0}$.

La única diferencia es si incorporar las fuerzas generalizadas en la energía potencial o escribirlas explícitamente como en el lado derecho, todas conducen a las mismas ecuaciones en la parte final. ${\displaystyle V_{j}}$ ${\displaystyle Q_{j}}$

De la segunda ley de Newton

A menudo resulta beneficioso utilizar la segunda ley de Newton en lugar de las ecuaciones de Lagrange , ya que las ecuaciones de Newton proporcionan las fuerzas de reacción en la articulación entre el péndulo y el carro. Estas ecuaciones dan lugar a dos ecuaciones para cada cuerpo: una en la dirección x y la otra en la dirección y. Las ecuaciones de movimiento del carro se muestran a continuación, donde el lado izquierdo es la suma de las fuerzas sobre el cuerpo y el lado derecho es la aceleración.

${\displaystyle F-R_{x}=M{\ddot {x}}}$

${\displaystyle F_{N}-R_{y}-Mg=0}$

En las ecuaciones anteriores , y son fuerzas de reacción en la articulación. es la fuerza normal aplicada al carro. Esta segunda ecuación depende únicamente de la fuerza de reacción vertical, por lo que la ecuación se puede utilizar para calcular la fuerza normal. La primera ecuación se puede utilizar para calcular la fuerza de reacción horizontal. Para completar las ecuaciones de movimiento, se debe calcular la aceleración de la masa puntual unida al péndulo. La posición de la masa puntual se puede dar en coordenadas inerciales como ${\displaystyle R_{x}}$ ${\displaystyle R_{y}}$ ${\displaystyle F_{N}}$

${\displaystyle {\vec {r}}_{P}=(x-\ell \sin \theta ){\hat {x}}_{I}+\ell \cos \theta {\hat {y}}_{I}}$

Tomando dos derivadas se obtiene el vector de aceleración en el marco de referencia inercial.

${\displaystyle {\vec {a}}_{P/I}=({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta ){\hat {x}}_{I}+(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta ){\hat {y}}_{I}}$

Luego, utilizando la segunda ley de Newton, se pueden escribir dos ecuaciones en la dirección x y en la dirección y. Nótese que las fuerzas de reacción son positivas cuando se aplican al péndulo y negativas cuando se aplican al carro. Esto se debe a la tercera ley de Newton.

${\displaystyle R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )}$

${\displaystyle R_{y}-mg=m(-\ell {\dot {\theta }}^{2}\cos \theta -\ell {\ddot {\theta }}\sin \theta )}$

La primera ecuación permite otra forma de calcular la fuerza de reacción horizontal en caso de que no se conozca la fuerza aplicada. La segunda ecuación se puede utilizar para calcular la fuerza de reacción vertical. La primera ecuación de movimiento se deriva sustituyendo en , lo que da como resultado ${\displaystyle F}$ ${\displaystyle F-R_{x}=M{\ddot {x}}}$ ${\displaystyle R_{x}=m({\ddot {x}}+\ell {\dot {\theta }}^{2}\sin \theta -\ell {\ddot {\theta }}\cos \theta )}$

${\displaystyle \left(M+m\right){\ddot {x}}-m\ell {\ddot {\theta }}\cos \theta +m\ell {\dot {\theta }}^{2}\sin \theta =F}$

Al observar esta ecuación, se ve que es idéntica al resultado del método de Lagrange. Para obtener la segunda ecuación, la ecuación de movimiento del péndulo debe estar marcada con un vector unitario que discurra perpendicularmente al péndulo en todo momento y que normalmente se indica como la coordenada x del marco del cuerpo. En coordenadas inerciales, este vector se puede escribir utilizando una simple transformación de coordenadas en 2D.

${\displaystyle {\hat {x}}_{B}=\cos \theta {\hat {x}}_{I}+\sin \theta {\hat {y}}_{I}}$

La ecuación de movimiento del péndulo escrita en forma vectorial es . Al poner puntos en ambos lados se obtiene lo siguiente en el lado izquierdo (nótese que una transposición es lo mismo que un producto escalar ) ${\displaystyle \sum {\vec {F}}=m{\vec {a}}_{P/I}}$ ${\displaystyle {\hat {x}}_{B}}$

${\displaystyle ({\hat {x}}_{B})^{T}\sum {\vec {F}}=({\hat {x}}_{B})^{T}(R_{x}{\hat {x}}_{I}+R_{y}{\hat {y}}_{I}-mg{\hat {y}}_{I})=({\hat {x}}_{B})^{T}(R_{p}{\hat {y}}_{B}-mg{\hat {y}}_{I})=-mg\sin \theta }$

En la ecuación anterior se utiliza la relación entre los componentes del marco corporal de las fuerzas de reacción y los componentes del marco inercial de las fuerzas de reacción. La suposición de que la barra que conecta la masa puntual al carro no tiene masa implica que esta barra no puede transferir ninguna carga perpendicular a la barra. Por lo tanto, los componentes del marco inercial de las fuerzas de reacción se pueden escribir simplemente como , lo que significa que la barra puede transferir cargas solo a lo largo del eje de la propia barra. Esto da lugar a otra ecuación que se puede utilizar para calcular la tensión en la propia barra: ${\displaystyle R_{p}{\hat {y}}_{B}}$

${\displaystyle R_{p}={\sqrt {R_{x}^{2}+R_{y}^{2}}}}$

El lado derecho de la ecuación se calcula de manera similar, punteando con la aceleración del péndulo. El resultado (después de algunas simplificaciones) se muestra a continuación. ${\displaystyle {\hat {x}}_{B}}$

${\displaystyle m({\hat {x}}_{B})^{T}({\vec {a}}_{P/I})=m({\ddot {x}}\cos \theta -\ell {\ddot {\theta }})}$

Combinando el LHS con el RHS y dividiendo por m se obtiene

${\displaystyle \ell {\ddot {\theta }}-g\sin \theta ={\ddot {x}}\cos \theta }$

Lo cual es idéntico al resultado del método de Lagrange. La ventaja de utilizar el método de Newton es que se revelan todas las fuerzas de reacción para garantizar que nada resulte dañado.

Variantes

Lograr la estabilidad de un péndulo invertido se ha convertido en un desafío de ingeniería común para los investigadores. ^[4] Existen diferentes variaciones del péndulo invertido en un carro que van desde una varilla en un carro hasta un péndulo invertido de múltiples segmentos en un carro. Otra variación coloca la varilla del péndulo invertido o la varilla segmentada en el extremo de un conjunto giratorio. En ambos, (el carro y el sistema giratorio) el péndulo invertido puede caer solo en un plano. Los péndulos invertidos en estos proyectos pueden requerirse para mantener el equilibrio solo después de que se logra una posición de equilibrio, o pueden lograr el equilibrio por sí mismos. Otra plataforma es un péndulo invertido de equilibrio de dos ruedas. La plataforma de dos ruedas tiene la capacidad de girar en el lugar, lo que ofrece una gran maniobrabilidad. ^[5] Otra variación más se equilibra en un solo punto. Una peonza , un monociclo o un péndulo invertido sobre una bola esférica, todos se equilibran en un solo punto.

Dibujo que muestra cómo se puede construir un péndulo Kapitza: un motor hace girar una manivela a alta velocidad, la manivela hace vibrar un brazo de palanca hacia arriba y hacia abajo, al que está unido el péndulo con un pivote.

El péndulo de Kapitza

Un péndulo invertido en el que el pivote oscila rápidamente hacia arriba y hacia abajo puede ser estable en la posición invertida. Esto se llama péndulo de Kapitza , en honor al físico ruso Pyotr Kapitza, quien lo analizó por primera vez. La ecuación de movimiento para un péndulo conectado a una base oscilante sin masa se deriva de la misma manera que para el péndulo en el carro. La posición de la masa puntual ahora está dada por:

${\displaystyle \left(-\ell \sin \theta ,y+\ell \cos \theta \right)}$

y la velocidad se encuentra tomando la primera derivada de la posición:

${\displaystyle v^{2}={\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}.}$

Gráficos del péndulo invertido sobre una base oscilatoria. El primer gráfico muestra la respuesta del péndulo en una oscilación lenta, el segundo la respuesta en una oscilación rápida.

El lagrangiano para este sistema se puede escribir como:

${\displaystyle L={\frac {1}{2}}m\left({\dot {y}}^{2}-2\ell {\dot {y}}{\dot {\theta }}\sin \theta +\ell ^{2}{\dot {\theta }}^{2}\right)-mg\left(y+\ell \cos \theta \right)}$

y la ecuación de movimiento se deduce de:

${\displaystyle {\mathrm {d} \over \mathrm {d} t}{\partial {L} \over \partial {\dot {\theta }}}-{\partial {L} \over \partial \theta }=0}$

Resultando en:

${\displaystyle \ell {\ddot {\theta }}-{\ddot {y}}\sin \theta =g\sin \theta .}$

Si y representa un movimiento armónico simple , , la siguiente ecuación diferencial es: ${\displaystyle y=A\sin \omega t}$

${\displaystyle {\ddot {\theta }}-{g \over \ell }\sin \theta =-{A \over \ell }\omega ^{2}\sin \omega t\sin \theta .}$

Esta ecuación no tiene soluciones elementales de forma cerrada, pero se puede explorar de diversas maneras. Se aproxima mucho a la ecuación de Mathieu , por ejemplo, cuando la amplitud de las oscilaciones es pequeña. Los análisis muestran que el péndulo se mantiene en posición vertical para oscilaciones rápidas. El primer gráfico muestra que cuando es una oscilación lenta, el péndulo cae rápidamente cuando se lo altera de la posición vertical. El ángulo excede los 90° después de un corto tiempo, lo que significa que el péndulo ha caído al suelo. Si es una oscilación rápida, el péndulo puede mantenerse estable alrededor de la posición vertical. El segundo gráfico muestra que cuando se lo altera de la posición vertical, el péndulo ahora comienza una oscilación alrededor de la posición vertical ( ). La desviación de la posición vertical se mantiene pequeña y el péndulo no se cae. ${\displaystyle y}$ ${\displaystyle \theta }$ ${\displaystyle y}$ ${\displaystyle \theta =0}$

Ejemplos

Podría decirse que el ejemplo más frecuente de un péndulo invertido estabilizado es el ser humano . Una persona de pie actúa como un péndulo invertido con los pies como pivote y, sin pequeños ajustes musculares constantes, se caería. El sistema nervioso humano contiene un sistema de control de retroalimentación inconsciente , el sentido del equilibrio o reflejo de enderezamiento , que utiliza la información propioceptiva de los ojos, los músculos y las articulaciones, y la información de orientación del sistema vestibular , que consiste en los tres canales semicirculares del oído interno y dos órganos otolíticos , para realizar pequeños ajustes continuos en los músculos esqueléticos para mantenernos de pie. Caminar, correr o mantener el equilibrio sobre una pierna exige más de este sistema. Ciertas enfermedades y la intoxicación por alcohol o drogas pueden interferir con este reflejo, causando mareos y desequilibrio , una incapacidad para mantenerse erguido. Una prueba de sobriedad de campo utilizada por la policía para evaluar la influencia del alcohol o las drogas en los conductores, prueba este reflejo para determinar si está alterado.

Algunos ejemplos sencillos incluyen equilibrar escobas o varas de medir con las manos.

El péndulo invertido se ha empleado en varios dispositivos y tratar de equilibrar un péndulo invertido presenta un problema de ingeniería único para los investigadores. ^[6] El péndulo invertido fue un componente central en el diseño de varios de los primeros sismómetros debido a su inestabilidad inherente que resulta en una respuesta medible a cualquier perturbación. ^[7]

El modelo de péndulo invertido se ha utilizado en algunos vehículos de transporte personal recientes , como los patinetes de dos ruedas con autoequilibrio y los monociclos eléctricos de una sola rueda . Estos dispositivos son cinemáticamente inestables y utilizan un sistema servo de retroalimentación electrónica para mantenerlos en posición vertical.

Hacer oscilar un péndulo en un carro hasta su estado de péndulo invertido se considera un problema/referencia tradicional de control óptimo de juguetes. ^{[8] [9]}

Trayectoria de un columpio de carrito de tiempo fijo que minimiza la fuerza al cuadrado

Véase también

• Péndulo doble invertido
• Péndulo de rueda de inercia
• Péndulo de Furuta
• iBOT
• Robot humanoide
• Robot con pelota

Referencias

1. Proyecto final de carrera de CA Hamilton Union College 1966
2. "Estabilidad del modelo de cohete".
3. Mitchell, Joe. "Técnicas para el péndulo oscilante y la ecuación de Mathieu" (PDF) . math.ou.edu . Consultado el 6 de noviembre de 2023 .
4. Ooi, Rich Chi. "Equilibrio de un robot autónomo de dos ruedas" (PDF) . robotics.ee.uwa.edu.au . Consultado el 6 de noviembre de 2023 .
5. "Copia archivada" (PDF) . Archivado desde el original (PDF) el 4 de marzo de 2016. Consultado el 1 de mayo de 2012 .{{cite web}}: CS1 maint: archived copy as title (link)
6. "Copia archivada" (PDF) . Archivado desde el original (PDF) el 4 de marzo de 2016. Consultado el 1 de mayo de 2012 .{{cite web}}: CS1 maint: archived copy as title (link)
7. "La historia temprana de la sismometría (hasta 1900)". Archivado desde el original el 28 de noviembre de 2009.
8. "El Acrobot y el Cart-Pole" (PDF) .
9. "Carrito de golf con pértiga". www.cs.huji.ac.il . Consultado el 19 de agosto de 2019 .

• D. Liberzon Conmutación en sistemas y control (2003 Springer) págs. 89 y siguientes

Lectura adicional

• Franklin y otros (2005). Control de sistemas dinámicos por retroalimentación, 5, Prentice Hall. ISBN 0-13-149930-0 

Enlaces externos

• YouTube - Péndulo invertido - Demostración n.° 3
• YouTube - péndulo invertido
• YouTube - Péndulo doble sobre un carro
• YouTube - Péndulo triple sobre un carro
• Simulación dinámica de un péndulo inverso sobre una base oscilatoria Archivado el 13 de septiembre de 2019 en Wayback Machine.
• Péndulo invertido: análisis, diseño e implementación
• Control no lineal de elevación y estabilización de un sistema de péndulo invertido
• Control difuso de estabilización de sistemas de péndulo invertido ^{[ enlace muerto permanente ]}
• Entrada de blog sobre el péndulo invertido, con código Python
• Ecuaciones de movimiento para la tarea de control de carros y postes