En geometría , la notación de Coxeter (también símbolo de Coxeter ) es un sistema de clasificación de grupos de simetría que describe los ángulos entre las reflexiones fundamentales de un grupo de Coxeter en una notación entre corchetes que expresa la estructura de un diagrama de Coxeter-Dynkin , con modificadores para indicar ciertos subgrupos. La notación recibe su nombre de HSM Coxeter y fue definida de manera más completa por Norman Johnson .
Para los grupos de Coxeter , definidos por reflexiones puras, existe una correspondencia directa entre la notación de corchetes y el diagrama de Coxeter-Dynkin . Los números en la notación de corchetes representan los órdenes de reflexión especular en las ramas del diagrama de Coxeter. Utiliza la misma simplificación, suprimiendo los 2 entre espejos ortogonales.
La notación de Coxeter se simplifica con exponentes para representar el número de ramas en una fila para un diagrama lineal. Por lo tanto, el grupo A n se representa mediante [3 n −1 ], lo que implica n nodos conectados por n−1 ramas de orden 3. Ejemplo A 2 = [3,3] = [3 2 ] o [3 1,1 ] representa diagramas
o
.
Coxeter inicialmente representó diagramas bifurcados con posicionamiento vertical de números, pero luego los abrevió con una notación exponencial, como [...,3 p,q ] o [3 p,q,r ], comenzando con [3 1,1,1 ] o [3,3 1,1 ] =
o como D 4 . Coxeter permitió ceros como casos especiales para ajustarse a la familia A n , como A 3 = [3,3,3,3] = [3 4,0,0 ] = [3 4,0 ] = [3 3,1 ] = [3 2,2 ], como=
=
.
Los grupos de Coxeter formados por diagramas cíclicos se representan mediante paréntesis dentro de corchetes, como [(p,q,r)] =
para el grupo de triángulos (pqr). Si los órdenes de ramificación son iguales, se pueden agrupar como un exponente como la longitud del ciclo entre paréntesis, como [(3,3,3,3)] = [3 [4] ], que representa el diagrama de Coxeter
o
.se puede representar como [3,(3,3,3)] o [3,3 [3] ].
También se pueden expresar con cuidado diagramas de bucles más complicados. El grupo de Coxeter paracompacto puede representarse mediante la notación de Coxeter [(3,3,(3),3,3)], con paréntesis anidados/superpuestos que muestran dos bucles [(3,3,3)] adyacentes, y también se representa de forma más compacta como [3 [ ]×[ ] ], que representa la simetría rómbica del diagrama de Coxeter. El diagrama de grafo completo paracompacto
o 
, se representa como [3 [3,3] ] con el superíndice [3,3] como la simetría de su diagrama de Coxeter tetraédrico regular .
Para los grupos afines e hiperbólicos, el subíndice es uno menos que el número de nodos en cada caso, ya que cada uno de estos grupos se obtuvo agregando un nodo al diagrama de un grupo finito.
El diagrama de Coxeter normalmente deja sin dibujar las ramas de orden 2, pero la notación de corchetes incluye un 2 explícito para conectar los subgrafos. Por lo tanto, el diagrama de Coxeter
= A 2 × A 2 = 2 A 2 se puede representar por [3]×[3] = [3] 2 = [3,2,3]. A veces, las ramas 2 explícitas se pueden incluir con una etiqueta 2 o con una línea con un espacio:
o, como una presentación idéntica a [3,2,3].
El rango del grupo de puntos de Coxeter es igual al número de nodos, que también es igual a la dimensión. Un único espejo existe en una dimensión, [ ],, mientras que en 2 dimensiones [1],
o [ ]×[ ] + . El 1 es un marcador de posición, no un orden de ramificación real, sino un marcador para un espejo inactivo ortogonal. La notación [ n ,1], representa un grupo de rango 3, como [ n ]×[ ] + o
. De manera similar, [1,1] como [ ]×[ ] + ×[ ] + oorden 2 y [1,1] + como [ ] + ×[ ] + ×[ ] + o, orden 1!
La notación de Coxeter representa la simetría rotacional/traslacional añadiendo un operador superíndice + fuera de los corchetes, [X] + que corta el orden del grupo [X] a la mitad, por lo tanto un subgrupo de índice 2. Este operador implica que se debe aplicar un número par de operadores, reemplazando las reflexiones con rotaciones (o traslaciones). Cuando se aplica a un grupo de Coxeter, se lo llama subgrupo directo porque lo que queda son solo isometrías directas sin simetría reflexiva.
Los operadores + también se pueden aplicar dentro de los corchetes, como [X,Y + ] o [X,(Y,Z) + ], y crean subgrupos "semidirectos" que pueden incluir generadores tanto reflexivos como no reflexivos. Los subgrupos semidirectos solo se pueden aplicar a subgrupos del grupo de Coxeter que tengan ramas de orden par adyacentes a él. A los elementos entre paréntesis dentro de un grupo de Coxeter se les puede dar un operador de superíndice + , que tiene el efecto de dividir las ramas ordenadas adyacentes en medio orden, por lo que generalmente solo se aplica con números pares. Por ejemplo, [4,3 + ] y [4,(3,3) + ] (
).
Si se aplica con una rama impar adyacente, no crea un subgrupo de índice 2, sino que crea dominios fundamentales superpuestos, como [5,1 + ] = [5/2], que pueden definir polígonos doblemente envueltos como un pentagrama , {5/2}, y [5,3 + ] se relaciona con el triángulo de Schwarz [5/2,3], densidad 2.
Los grupos sin elementos + vecinos se pueden ver en nodos anillados. El diagrama de Coxeter-Dynkin para politopos uniformes y los panales de abejas están relacionados con nodos huecos alrededor de los elementos + , círculos vacíos con los nodos alternados eliminados. Por lo tanto, el cubo romo ,
tiene simetría [4,3] + (), y el tetraedro romo ,tiene simetría [4,3 + ] (), y un semicubo , h{4,3} = {3,3} (o
=
) tiene simetría [1 + ,4,3] = [3,3] (o
==).
Nota: Simetría piritoédrica se puede escribir como
, separando el gráfico con espacios para mayor claridad, con los generadores {0,1,2} del grupo de Coxeter
, produciendo generadores piritoédricos {0,12}, una reflexión y una rotación triple. Y la simetría tetraédrica quiral se puede escribir como o , [1 + ,4,3 + ] = [3,3] + , con generadores {12,0120}.
Johnson extiende el operador + para trabajar con un marcador de posición 1 + nodos, lo que elimina los espejos, duplicando el tamaño del dominio fundamental y corta el orden del grupo a la mitad. [1] En general, esta operación solo se aplica a espejos individuales delimitados por ramas de orden par. El 1 representa un espejo, por lo que [2p] puede verse como [2p, 1 ], [ 1 ,2p] o [ 1 ,2p, 1 ], como en el diagrama
o
, con 2 espejos relacionados por un ángulo diedro de orden 2p. El efecto de la eliminación de un espejo es duplicar los nodos de conexión, lo que se puede ver en los diagramas de Coxeter:=
, o en notación entre paréntesis:[1 + ,2p, 1 ] = [ 1 ,p, 1 ] = [p].
Cada uno de estos espejos se puede eliminar de modo que h[2p] = [1 + ,2p,1] = [1,2p,1 + ] = [p], un índice de subgrupo reflexivo 2. Esto se puede mostrar en un diagrama de Coxeter agregando un símbolo + sobre el nodo:==.
Si se eliminan ambos espejos, se genera un cuarto de subgrupo, y el orden de rama se convierte en un punto de giro de la mitad del orden:
==== 
.Por ejemplo, (con p=2): [4,1 + ] = [1 + ,4] = [2] = [ ]×[ ], orden 4. [1 + ,4,1 + ] = [2] + , orden 2.
Lo opuesto a reducir a la mitad es duplicar [2], que agrega un espejo, divide en dos un dominio fundamental y duplica el orden del grupo.
Las operaciones de reducción a la mitad se aplican a grupos de rango superior, como la simetría tetraédrica , que es un semigrupo de un grupo octaédrico : h[4,3] = [1 + ,4,3] = [3,3], eliminando la mitad de los espejos en la rama 4. El efecto de la eliminación de un espejo es duplicar todos los nodos de conexión, lo que se puede ver en los diagramas de Coxeter:
=
, h[2p,3] = [1 + ,2p,3] = [(p,3,3)].
Si los nodos están indexados, los subgrupos de la mitad se pueden etiquetar con nuevos espejos como compuestos., generadores {0,1} tiene subgrupo=
, generadores {1,010}, donde se elimina el espejo 0 y se reemplaza por una copia del espejo 1 reflejada en el espejo 0. También se proporciona, generadores {0,1,2}, tiene medio grupo=, generadores {1,2,010}.
La duplicación mediante la adición de un espejo también se aplica para invertir la operación de reducción a la mitad: [[3,3]] = [4,3], o más generalmente [[(q,q,p)]] = [2p,q].
Johnson también agregó un operador asterisco o estrella * para los subgrupos "radicales", [3] que actúa de manera similar al operador + , pero elimina la simetría rotacional. El índice del subgrupo radical es el orden del elemento eliminado. Por ejemplo, [4,3*] ≅ [2,2]. El subgrupo [3] eliminado es de orden 6, por lo que [2,2] es un subgrupo de índice 6 de [4,3].
Los subgrupos radicales representan la operación inversa a una operación de simetría extendida. Por ejemplo, [4,3*] ≅ [2,2], y a la inversa, [2,2] puede extenderse como [3[2,2]] ≅ [4,3]. Los subgrupos pueden expresarse como un diagrama de Coxeter:
o
≅
El nodo eliminado (espejo) hace que los espejos virtuales adyacentes se conviertan en espejos reales.
Si [4,3] tiene generadores {0,1,2}, [4,3 + ], índice 2, tiene generadores {0,12}; [1 + ,4,3] ≅ [3,3], índice 2 tiene generadores {010,1,2}; mientras que el subgrupo radical [4,3*] ≅ [2,2], índice 6, tiene generadores {01210, 2, (012) 3 }; y finalmente [1 + ,4,3*], índice 12 tiene generadores {0(12) 2 0, (012) 2 01}.
Un subgrupo triónico es un subgrupo de índice 3. Johnson define un subgrupo triónico con operador ⅄, índice 3. Para grupos de Coxeter de rango 2, [3], el subgrupo triónico, [3 ⅄ ] es [ ], un espejo simple. Y para [3 p ], el subgrupo triónico es [3 p ] ⅄ ≅ [ p ]. Dado
, con generadores {0,1}, tiene 3 subgrupos triónicos. Se pueden diferenciar poniendo el símbolo ⅄ al lado del generador de espejo que se va a eliminar, o en una rama para ambos: [3 p ,1 ⅄ ] =
=
, =, y [3 p ⅄ ] =
=con generadores {0,10101}, {01010,1} o {101,010}.
Subgrupos triónicos de simetría tetraédrica: [3,3] ⅄ ≅ [2 + ,4], relacionando la simetría del tetraedro regular y el difenoide tetragonal .
Para los grupos de Coxeter de rango 3, [ p ,3], hay un subgrupo triónico [ p ,3 ⅄ ] ≅ [ p /2, p ], o=
. Por ejemplo, el grupo finito [4,3 ⅄ ] ≅ [2,4], el grupo euclidiano [6,3 ⅄ ] ≅ [3,6], y el grupo hiperbólico [8,3 ⅄ ] ≅ [4,8].
Una rama adyacente de orden impar, p , no reducirá el orden del grupo, sino que creará dominios fundamentales superpuestos. El orden del grupo permanece igual, mientras que la densidad aumenta. Por ejemplo, la simetría icosaédrica , [5,3], del icosaedro de poliedros regulares se convierte en [5/2,5], la simetría de 2 poliedros regulares en estrella. También relaciona los teselados hiperbólicos {p,3} y los teselados hiperbólicos en estrella {p/2,p}
Para el rango 4, [ q ,2 p ,3 ⅄ ] = [2 p ,((p,q,q))],
=
.
Por ejemplo, [3,4,3 ⅄ ] = [4,3,3], o
=
, generadores {0,1,2,3} en [3,4,3] con el subgrupo triónico [4,3,3] generadores {0,1,2,32123}. Para grupos hiperbólicos, [3,6,3 ⅄ ] = [6,3 [3] ], y [4,4,3 ⅄ ] = [4,4,4].
Johnson identificó dos subgrupos triónicos específicos [4] de [3,3], primero un subgrupo de índice 3 [3,3] ⅄ ≅ [2 + ,4], con [3,3] (==
) generadores {0,1,2}. También se puede escribir como [(3,3,2 ⅄ )] () como recordatorio de sus generadores {02,1}. Esta reducción de simetría es la relación entre el tetraedro regular y el difenoide tetragonal , representan un estiramiento de un tetraedro perpendicular a dos aristas opuestas.
En segundo lugar, identifica un subgrupo de índice 6 relacionado [3,3] Δ o [(3,3,2 ⅄ )] + (), índice 3 de [3,3] + ≅ [2,2] + , con generadores {02,1021}, de [3,3] y sus generadores {0,1,2}.
Estos subgrupos también se aplican dentro de grupos de Coxeter más grandes con el subgrupo [3,3] con ramas vecinas, todas de orden par.
Por ejemplo, [(3,3) + ,4], [(3,3) ⅄ ,4] y [(3,3) Δ ,4] son subgrupos de [3,3,4], índice 2, 3 y 6 respectivamente. Los generadores de [(3,3) ⅄ ,4] ≅ [[4,2,4]] ≅ [8,2 + ,8], orden 128, son {02,1,3} de los generadores de [3,3,4] {0,1,2,3}. Y [(3,3) Δ ,4] ≅ [[4,2 + ,4]], orden 64, tiene generadores {02,1021,3}. Asimismo, [3 ⅄ ,4,3 ⅄ ] ≅ [(3,3) ⅄ ,4].
También relacionado [3 1,1,1 ] = [3,3,4,1 + ] tiene subgrupos triónicos: [3 1,1,1 ] ⅄ = [(3,3) ⅄ ,4,1 + ], orden 64, y 1=[3 1,1,1 ] Δ = [(3,3) Δ ,4,1 + ] ≅ [[4,2 + ,4]] + , orden 32.
Una inversión central , de orden 2, es operativamente diferente por dimensión. El grupo [ ] n = [2 n −1 ] representa n espejos ortogonales en un espacio n-dimensional, o un subespacio n-plano de un espacio dimensional superior. Los espejos del grupo [2 n −1 ] están numerados . El orden de los espejos no importa en el caso de una inversión. La matriz de una inversión central es , la matriz Identidad con menos uno en la diagonal.
A partir de esa base, la inversión central tiene un generador como producto de todos los espejos ortogonales. En la notación de Coxeter, este grupo de inversión se expresa añadiendo una alternancia + a cada rama 2. La simetría de alternancia se marca en los nodos del diagrama de Coxeter como nodos abiertos.
Un diagrama de Coxeter-Dynkin se puede marcar con 2 ramas explícitas que definen una secuencia lineal de espejos, nodos abiertos y nodos doblemente abiertos compartidos para mostrar el encadenamiento de los generadores de reflexión.
Por ejemplo, [2 + ,2] y [2,2 + ] son subgrupos índice 2 de [2,2],, y se representan como(o) y(o) con generadores {01,2} y {0,12} respectivamente. Su índice de subgrupo común 4 es [2 + ,2 + ], y está representado por
(o), con la doble aperturamarcando un nodo compartido en las dos alternancias, y un único generador de rotoreflexión {012}.
Las rotaciones y reflexiones rotatorias se construyen mediante un único producto monogenerador de todas las reflexiones de un grupo prismático, [2 p ]×[2 q ]×... donde mcd ( p , q ,...)=1, son isomorfos al grupo cíclico abstracto Z n , de orden n =2 pq .
Las rotaciones dobles de cuatro dimensiones, [2 p + ,2 + ,2 q + ] (con mcd ( p , q )=1), que incluyen un grupo central, y se expresan por Conway como ±[C p ×C q ], [5] orden 2 pq . Del diagrama de Coxeter, generadores {0,1,2,3}, requiere dos generadores para [2 p + ,2 + ,2 q + ],como {0123,0132}. Semigrupos, [2 p + ,2 + ,2 q + ] + , o gráfico cíclico, [(2 p + ,2 + ,2 q + ,2 + )],expresado por Conway es [C p ×C q ], orden pq , con un generador, como {0123}.
Si hay un factor común f , la doble rotación se puede escribir como 1 ⁄ f [2 pf + ,2 + ,2 qf + ] (con mcd ( p , q )=1), generadores {0123,0132}, orden 2 pqf . Por ejemplo, p = q =1, f =2, 1 ⁄ 2 [4 + ,2 + ,4 + ] es orden 4. Y 1 ⁄ f [2 pf + ,2 + ,2 qf + ] + , generador {0123}, es orden pqf . Por ejemplo, 1 ⁄ 2 [4 + ,2 + ,4 + ] + es orden 2, una inversión central .
En general, un grupo de n -rotación, [2 p 1 + ,2,2 p 2 + ,2,..., p n + ] puede requerir hasta n generadores si mcd( p 1 ,.., p n )>1, como producto de todos los espejos, y luego intercambiando pares secuenciales. El semigrupo, [2 p 1 + ,2,2 p 2 + ,2,..., p n + ] + tiene generadores al cuadrado. Las reflexiones n -rotativas son similares.
Los grupos simples con solo elementos de ramificación de orden impar tienen solo un único subgrupo rotacional/traslacional de orden 2, que también es el subgrupo conmutador , ejemplos [3,3] + , [3,5] + , [3,3,3] + , [3,3,5] + . Para otros grupos de Coxeter con ramas de orden par, el subgrupo conmutador tiene índice 2 c , donde c es el número de subgrafos desconectados cuando se eliminan todas las ramas de orden par. [6]
Por ejemplo, [4,4] tiene tres nodos independientes en el diagrama de Coxeter cuando se eliminan los 4 s, por lo que su subgrupo conmutador es de índice 2 3 , y puede tener diferentes representaciones, todas con tres operadores + : [4 + ,4 + ] + , [1 + ,4,1 + ,4,1 + ], [1 + ,4,4,1 + ] + , o [(4 + ,4 + ,2 + )]. Se puede utilizar una notación general con + c como exponente de grupo, como [4,4] +3 .
Los grupos de simetría diedral con órdenes pares tienen varios subgrupos. Este ejemplo muestra dos espejos generadores de [4] en rojo y verde, y analiza todos los subgrupos por reducción a la mitad, reducción de rango y sus subgrupos directos. El grupo [4],tiene dos generadores de espejos 0 y 1. Cada uno genera dos espejos virtuales 101 y 010 por reflexión en el otro.
El grupo [4,4] tiene 15 subgrupos de índice pequeños. Esta tabla los muestra todos, con un dominio fundamental amarillo para grupos reflexivos puros y dominios blancos y azules alternados que se emparejan para formar dominios rotacionales. Las líneas de espejo cian, rojo y verde corresponden a los nodos del mismo color en el diagrama de Coxeter. Los generadores de subgrupos se pueden expresar como productos de los 3 espejos originales del dominio fundamental, {0,1,2}, correspondientes a los 3 nodos del diagrama de Coxeter.. Un producto de dos líneas de reflexión que se intersecan produce una rotación, como {012}, {12} o {02}. Quitar un espejo provoca dos copias de espejos vecinos, a través del espejo eliminado, como {010} y {212}. Dos rotaciones en serie reducen el orden de rotación a la mitad, como {0101} o {(01) 2 }, {1212} o {(02) 2 }. Un producto de los tres espejos crea una transreflexión , como {012} o {120}.
El mismo conjunto de 15 subgrupos pequeños existe en todos los grupos de triángulos con elementos de orden par, como [6,4] en el plano hiperbólico:
Un subgrupo parabólico de un grupo de Coxeter se puede identificar eliminando uno o más espejos generadores representados con un diagrama de Coxeter. Por ejemplo, el grupo octaédricotiene subgrupos parabólicos,,,,,. En la notación entre corchetes [4,3] hay subgrupos parabólicos [4],[2],[3] y un espejo único []. Se conoce el orden del subgrupo y siempre es un orden de grupo divisor entero o índice. Los subgrupos parabólicos también se pueden escribir con x nodos, como=[4,3] subgrupo eliminando el segundo espejo:o== [4,1 × ,3] = [2].
Un subgrupo de Petrie de un grupo de Coxeter irreducible se puede crear mediante el producto de todos los generadores. Se puede ver en el polígono de Petrie regular oblicuo de un politopo regular . El orden del nuevo grupo se llama número de Coxeter del grupo de Coxeter original. El número de Coxeter de un grupo de Coxeter es 2 m / n , donde n es el rango y m es el número de reflexiones. Un subgrupo de Petrie se puede escribir con un superíndice π . Por ejemplo, [3,3] π es el subgrupo de Petrie de un grupo tetraédrico, grupo cíclico de orden 4, generado por una rotorreflexión . Un grupo de Coxeter de rango 4 tendrá un generador de doble rotación , como [4,3,3] π es de orden 8.
La notación de Coxeter incluye la notación de corchetes dobles, [[X]] para expresar simetría automórfica dentro de un diagrama de Coxeter. Johnson agregó una duplicación alternativa mediante corchetes angulares <[X]>. Johnson también agregó un modificador de simetría de prefijo [Y[X]], donde Y puede representar la simetría del diagrama de Coxeter de [X] o la simetría del dominio fundamental de [X].
Por ejemplo, en 3D estos diagramas geométricos rectangulares y rómbicos equivalentes son :y, el primero duplicado con corchetes, [[3 [4] ]] o duplicado dos veces como [2[3 [4] ]], con [2], simetría superior de orden 4. Para diferenciar el segundo, se utilizan corchetes angulares para duplicar, <[3 [4] ]> y duplicado dos veces como <2[3 [4] ]>, también con una simetría diferente de [2], orden 4. Finalmente, una simetría completa donde los 4 nodos son equivalentes se puede representar por [4[3 [4] ]], con la simetría de orden 8, [4] del cuadrado . Pero al considerar el dominio fundamental del disfenoides tetragonal , la simetría extendida [4] del grafo cuadrado se puede marcar de forma más explícita como [(2 + ,4)[3 [4] ]] o [2 + ,4[3 [4] ]].
Existe simetría adicional en los diagramas cíclicos y ramificados , y . tiene simetría de orden 2 n de un n -gono regular, { n }, y se representa por [ n [3 [ n ] ]]. y se representan por [3[3 1,1,1 ]] = [3,4,3] y [3[3 2,2,2 ]] respectivamente mientras que por [(3,3)[3 1,1,1,1 ]] = [3,3,4,3], con el diagrama que contiene la simetría de orden 24 del tetraedro regular , {3,3}. El grupo hiperbólico paracompacto = [3 1,1,1,1,1 ],
, contiene la simetría de una celda de 5 , {3,3,3}, y por lo tanto está representada por [(3,3,3)[3 1,1,1,1,1 ]] = [3,4,3,3,3].
Un superíndice asterisco * es efectivamente una operación inversa, que crea subgrupos radicales eliminando los espejos conectados de orden impar. [7]
Ejemplos:
Al observar los generadores, la doble simetría se ve como la adición de un nuevo operador que mapea posiciones simétricas en el diagrama de Coxeter, haciendo que algunos generadores originales sean redundantes. Para los grupos espaciales 3D y los grupos puntuales 4D, Coxeter define un subgrupo de índice dos de [[X]], [[X] + ], que define como el producto de los generadores originales de [X] por el generador de duplicación. Esto parece similar a [[X]] + , que es el subgrupo quiral de [[X]]. Entonces, por ejemplo, los grupos espaciales 3D [[4,3,4]] + (I432, 211) y [[4,3,4] + ] (Pm 3 n, 223) son subgrupos distintos de [[4,3,4]] (Im 3 m, 229).
En una dimensión, el grupo bilateral [ ] representa una simetría especular única, abstracta Dih 1 o Z 2 , orden de simetría 2. Se representa como un diagrama de Coxeter-Dynkin con un solo nodo,El grupo identidad es el subgrupo directo [ ] + , Z 1 , orden de simetría 1. El superíndice + simplemente implica que se ignoran las reflexiones especulares alternadas, lo que deja al grupo identidad en este caso más simple. Coxeter utilizó un solo nodo abierto para representar una alternancia,.
En dos dimensiones, el grupo rectangular [2], abstracto D 2 2 o D 4 , también se puede representar como un producto directo [ ]×[ ], al ser el producto de dos grupos bilaterales, representa dos espejos ortogonales, con diagrama de Coxeter,, con orden 4. El 2 en [2] proviene de la linealización de los subgrafos ortogonales en el diagrama de Coxeter, comocon orden de ramificación explícito 2. El grupo rómbico , [2] + (o), la mitad del grupo rectangular, la simetría de reflexión puntual , Z 2 , orden 2.
Notación de Coxeter para permitir un marcador de posición 1 para grupos de rango inferior, por lo que [1] es lo mismo que [ ], y [1 + ] o [1] + es lo mismo que [ ] + y diagrama de Coxeter.
El grupo p-gonal completo [p], grupo diedro abstracto D 2 p , ( no abeliano para p>2), de orden 2 p , es generado por dos espejos en ángulo π / p , representado por el diagrama de Coxeter. El subgrupo p-gonal [p] + , grupo cíclico Z p , de orden p , generado por un ángulo de rotación de π / p .
La notación de Coxeter utiliza corchetes dobles para representar una duplicación automórfica de la simetría mediante la adición de un espejo bisectriz al dominio fundamental . Por ejemplo, [[p]] agrega un espejo bisectriz a [p] y es isomorfo a [2p].
En el límite, bajando a una dimensión, el grupo apeirogonal completo se obtiene cuando el ángulo tiende a cero, por lo que [∞], abstractamente el grupo diedro infinito D ∞ , representa dos espejos paralelos y tiene un diagrama de Coxeter.
. El grupo apeirogonal [∞] + ,, de manera abstracta, el grupo cíclico infinito Z ∞ , isomorfo al grupo aditivo de los números enteros , se genera mediante una única traslación distinta de cero.
En el plano hiperbólico, hay un grupo pseudogonal completo [ iπ/λ ], y un subgrupo pseudogonal [ iπ/λ ] + ,
Estos grupos existen en polígonos regulares de lados infinitos, con una longitud de arista λ. Los espejos son todos ortogonales a una sola línea.
Los grupos de puntos en 3 dimensiones se pueden expresar en notación entre corchetes relacionados con los grupos de Coxeter de rango 3:
En tres dimensiones, el grupo ortorrómbico completo u ortorrectangular [2,2], abstractamente Z 2 3 , orden 8, representa tres espejos ortogonales (también representados por el diagrama de Coxeter como tres puntos separados).). También se puede representar como un producto directo [ ]×[ ]×[ ], pero la expresión [2,2] permite definir subgrupos:
En primer lugar, existe un subgrupo "semidirecto", el grupo ortorrómbico , [2,2 + ] (o), de manera abstracta Z 2 × Z 2 , de orden 4. Cuando el superíndice + se da dentro de los corchetes, significa reflexiones generadas solo desde los espejos adyacentes (como se define en el diagrama de Coxeter,) se alternan. En general, los órdenes de ramificación vecinos al nodo + deben ser pares. En este caso [2,2 + ] y [2 + ,2] representan dos subgrupos isomorfos que son geométricamente distintos. Los otros subgrupos son el grupo pararómbico [2,2] + (o), también de orden 4, y finalmente el grupo central [2 + ,2 + ] (o) de orden 2.
A continuación está el grupo ortogonal completo , [2,p] (), de manera abstracta Z 2 ×D 2 p , de orden 4p, que representa dos espejos en un ángulo diedro π/ p , y ambos son ortogonales a un tercer espejo. También se representa mediante el diagrama de Coxeter como.
El subgrupo directo se llama grupo para- p -gonal, [2,p] + (o), de manera abstracta D 2 p , de orden 2p, y otro subgrupo es [2,p + ] () de forma abstracta Z 2 × Z p , también de orden 2p.
El grupo giro-p-gonal completo , [2 + ,2 p ] (o), de manera abstracta D 4 p , de orden 4 p . El grupo giro- p -gonal, [2 + ,2p + ] (o), de manera abstracta Z 2 p , de orden 2 p es un subgrupo tanto de [2 + ,2 p ] como de [2,2 p + ].
Los grupos poliédricos se basan en la simetría de los sólidos platónicos : el tetraedro , el octaedro , el cubo , el icosaedro y el dodecaedro , con símbolos de Schläfli {3,3}, {3,4}, {4,3}, {3,5} y {5,3} respectivamente. Los grupos de Coxeter para estos son: [3,3] (), [3,4] (), [3,5] (
) llamada simetría tetraédrica completa , simetría octaédrica y simetría icosaédrica , con órdenes de 24, 48 y 120.
En todas estas simetrías, las reflexiones alternas se pueden eliminar produciendo el tetraedro rotacional [3,3] + (), octaédrico [3,4] + (), y icosaédrica [3,5] + () grupos de orden 12, 24 y 60. El grupo octaédrico también tiene un subgrupo de índice 2 único llamado grupo de simetría piritoédrica , [3 + ,4] (o), de orden 12, con una mezcla de simetría rotacional y reflexiva. La simetría piritoédrica es también un subgrupo de índice 5 de la simetría icosaédrica:-->, con espejo virtual 1 en 0 , {010} y rotación triple {12}.
El grupo tetraédrico, [3,3] (), tiene una duplicación [[3,3]] (que puede representarse mediante nodos coloreados), mapeando el primer y el último espejo entre sí, y esto produce el [3,4] (o) grupo. El subgrupo [3,4,1 + ] (o) es lo mismo que [3,3], y [3 + ,4,1 + ] (o) es lo mismo que [3,3] + .
En el plano euclidiano hay 3 grupos reflexivos fundamentales generados por 3 espejos, representados por diagramas de Coxeter.,
, y, y se les da la notación de Coxeter como [4,4], [6,3] y [(3,3,3)]. Los paréntesis del último grupo implican el ciclo del diagrama y también tienen una notación abreviada [3 [3] ].
[[4,4]] como una duplicación del grupo [4,4] produjo la misma simetría rotada π/4 del conjunto original de espejos.
Los subgrupos directos de simetría rotacional son: [4,4] + , [6,3] + , y [(3,3,3)] + . [4 + ,4] y [6,3 + ] son subgrupos semidirectos.
Dados en notación de Coxeter ( notación orbifold ), algunos subgrupos afines de índice bajo son:
Los grupos de rango cuatro definen los grupos de puntos de cuatro dimensiones :
Los grupos de rango cuatro también definen los grupos de líneas tridimensionales :
Los grupos de rango cuatro definen los grupos duoprismáticos de cuatro dimensiones. En el límite, cuando p y q tienden al infinito, degeneran en dos dimensiones y en los grupos de papel tapiz.
Los grupos de rango cuatro también definieron algunos de los grupos de papel tapiz bidimensionales , como casos límite de los grupos de duoprismas de cuatro dimensiones:
Los subgrupos de [∞,2,∞], (*2222) se pueden expresar hasta su subgrupo conmutador de índice 16:
La notación de Coxeter se ha extendido al espacio complejo , C n donde los nodos son reflexiones unitarias de período 2 o mayor. Los nodos se etiquetan con un índice, que se supone que es 2 para la reflexión real ordinaria si se suprime. Los grupos de reflexión complejos se denominan grupos de Shephard en lugar de grupos de Coxeter , y se pueden utilizar para construir politopos complejos .
En , un grupo Shephard de rango 1
, orden p , se representa como p [ ], [ ] p o ] p [. Tiene un solo generador, que representa una rotación de 2 π / p radianes en el plano complejo : .
Coxeter escribe el grupo complejo de rango 2, p [ q ] r representa el diagrama de Coxeter 
. p y r solo se deben suprimir si ambos son 2, que es el caso real [ q ]. El orden de un grupo de rango 2 p [ q ] r es . [9]
Las soluciones de rango 2 que generan polígonos complejos son: p [4] 2 ( p es 2,3,4,...), 3 [3] 3 , 3 [6] 2 , 3 [4] 3 , 4 [3 ] 4 , 3 [8] 2 , 4 [6] 2 , 4 [4] 3 , 3 [5 ] 3 , 5 [3] 5 , 3 [10] 2 , 5 [6] 2 y 5 [4] 3 con diagramas de Coxeter,
,,,
,
,,,,
,
,,.
Los grupos infinitos son 3 [12] 2 , 4 [8] 2 , 6 [6 ] 2 , 3 [6] 3 , 6 [4] 3 , 4 [4] 4 y 6 [3] 6 o
,,
,,,,.
Los subgrupos de índice 2 existen eliminando una reflexión real: p [2 q ] 2 → p [ q ] p . También existen subgrupos de índice r para 4 ramas: p [4] r → p [ r ] p .
Para la familia infinita p [4] 2 , para cualquier p = 2, 3, 4,..., hay dos subgrupos: p [4] 2 → [ p ], índice p , mientras que p [4] 2 → p [ ]× p [ ], índice 2.
Un grupo de Coxeter, representado por el diagrama de Coxeter , se da la notación de Coxeter [p,q] para los órdenes de ramificación. Cada nodo en el diagrama de Coxeter representa un espejo, por convención llamado ρ i (y matriz R i ). Los generadores de este grupo [p,q] son reflexiones: ρ 0 , ρ 1 y ρ 2 . La subsimetría rotacional se da como productos de reflexiones: Por convención, σ 0,1 (y matriz S 0,1 ) = ρ 0 ρ 1 representa una rotación de ángulo π/p, y σ 1,2 = ρ 1 ρ 2 es una rotación de ángulo π/q, y σ 0,2 = ρ 0 ρ 2 representa una rotación de ángulo π/2.
[p,q] + ,, es un subgrupo de índice 2 representado por dos generadores de rotación, cada uno producto de dos reflexiones: σ 0,1 , σ 1,2 , y que representan rotaciones de ángulos π/ p y π/ q respectivamente.
Con una rama par, [ p + ,2 q ],o, es otro subgrupo del índice 2, representado por el generador de rotación σ 0,1 , y el reflexivo ρ 2 .
Con ramas pares, [2 p + ,2 q + ],, es un subgrupo de índice 4 con dos generadores, construido como producto de las tres matrices de reflexión: Por convención como: ψ 0,1,2 y ψ 1,2,0 , que son reflexiones rotatorias , que representan una reflexión y una rotación o reflexión.
En el caso de grupos de Coxeter afines como, o, un espejo, normalmente el último, se traslada desde el origen. Un generador de traslación τ 0,1 (y matriz T 0,1 ) se construye como el producto de dos (o un número par de) reflexiones, incluida la reflexión afín. Una transreflexión (reflexión más una traslación) puede ser el producto de un número impar de reflexiones φ 0,1,2 (y matriz V 0,1,2 ), como el subgrupo de índice 4: [4 + ,4 + ] =.
Otro generador compuesto, por convención como ζ (y matriz Z), representa la inversión , asignando un punto a su inverso. Para [4,3] y [5,3], ζ = (ρ 0 ρ 1 ρ 2 ) h/2 , donde h es 6 y 10 respectivamente, el número de Coxeter para cada familia. Para el grupo de Coxeter 3D [p,q] (), este subgrupo es una reflexión rotatoria [2 + ,h + ].
Los grupos de Coxeter se clasifican por su rango, que es el número de nodos en su diagrama de Coxeter-Dynkin . La estructura de los grupos también se da con sus tipos de grupos abstractos: En este artículo, los grupos diedros abstractos se representan como Dih n , y los grupos cíclicos se representan como Z n , con Dih 1 = Z 2 .
Por ejemplo, en 2D, el grupo de Coxeter [ p ] () está representada por dos matrices de reflexión R 0 y R 1 , La simetría cíclica [ p ] + () está representado por el generador de rotación de la matriz S 0,1 .
Los grupos de Coxeter de rango finito 3 son [1, p ], [2, p ], [3,3], [3,4] y [3,5].
Para reflejar un punto a través de un plano (que pasa por el origen), se puede utilizar , donde es la matriz identidad 3×3 y es el vector unitario tridimensional para la normal vectorial del plano. Si la norma L2 de y es la unidad, la matriz de transformación se puede expresar como:
El grupo reflexivo finito tridimensional reducible es de simetría diedra , [ p ,2], orden 4 p ,. Los generadores de reflexión son las matrices R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Identidad. [ p ,2] + () se genera mediante 2 de 3 rotaciones: S 0,1 , S 1,2 y S 0,2 . Una rotoreflexión de orden p se genera mediante V 0,1,2 , el producto de las 3 reflexiones.
El grupo reflexivo finito tridimensional irreducible más simple es de simetría tetraédrica , [3,3], orden 24,. Los generadores de reflexión, de una construcción D 3 = A 3 , son las matrices R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Identidad. [3,3] + () se genera mediante 2 de 3 rotaciones: S 0,1 , S 1,2 y S 0,2 . Un subgrupo triónico, isomorfo a [2 + ,4], de orden 8, se genera mediante S 0,2 y R 1 . Una rotorreflexión de orden 4 se genera mediante V 0,1,2 , el producto de las 3 reflexiones.
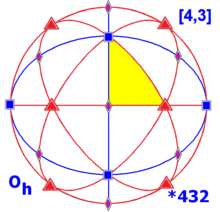
Otro grupo reflexivo finito tridimensional irreducible es la simetría octaédrica , [4,3], orden 48,. Las matrices generadoras de reflexión son R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 4 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Identidad. Simetría octaédrica quiral, [4,3] + , () se genera mediante 2 de 3 rotaciones: S 0,1 , S 1,2 y S 0,2 . Simetría piritoédrica [4,3 + ], () se genera por la reflexión R 0 y la rotación S 1,2 . Una rotorreflexión de 6 pliegues se genera por V 0,1,2 , el producto de las 3 reflexiones.
Un grupo reflexivo finito tridimensional irreducible final es la simetría icosaédrica , [5,3], orden 120,. Las matrices generadoras de reflexión son R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 5 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Identidad. [5,3] + () se genera mediante 2 de 3 rotaciones: S 0,1 , S 1,2 y S 0,2 . Una rotorreflexión de 10 veces se genera mediante V 0,1,2 , el producto de las 3 reflexiones.
Hay 4 grupos de Coxeter irreducibles en 4 dimensiones: [3,3,3], [4,3,3], [3 1,1,1 ], [3,4,4], [5,3,3], así como una familia infinita de grupos duoprismáticos [ p ,2, q ].
El grupo duprismático, [ p ,2, q ], tiene orden 4 pq .
El grupo duoprismático puede duplicarse en orden, hasta 8 p 2 , con una rotación doble entre los dos planos.
La simetría hipertetraédrica, [3,3,3], orden 120, es más fácil de representar con 4 espejos en 5 dimensiones, como un subgrupo de [4,3,3,3].
El grupo extendido [[3,3,3]], de orden 240, se duplica mediante una matriz de rotación doble T, invirtiendo aquí el orden de coordenadas y el signo: Hay 3 generadores {T, R 0 , R 1 }. Como T es autorrecíproco, R 3 =TR 0 T y R 2 =TR 1 T.
Un grupo reflexivo finito de 4 dimensiones irreducible es un grupo hiperoctaédrico (o grupo hexadecacórico (para 16 celdas ), B 4 = [4,3,3], orden 384,. Las matrices generadoras de reflexión son R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 4 =( R 1 × R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Identidad.
Simetría hiperoctaédrica quiral, [4,3,3] + , () se genera mediante 3 de 6 rotaciones: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 y S 0,3 . Simetría hiperpiritoédrica [4,(3,3) + ], () se genera por la reflexión R 0 y las rotaciones S 1,2 y S 2,3 . Una rotación doble de 8 veces se genera por W 0,1,2,3 , el producto de las 4 reflexiones.
Un semigrupo de [4,3,3] es [3,3 1,1 ],
, orden 192. Comparte 3 generadores con el grupo [4,3,3], pero tiene dos copias de un generador adyacente, uno reflejado a través del espejo eliminado.
Un grupo reflexivo finito de 4 dimensiones irreducible es el grupo icositetracórico (para 24 celdas ), F 4 = [3,4,3], orden 1152,. Las matrices generadoras de reflexión son R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 3 =( R 1 × R 2 ) 4 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Identidad.
Simetría icositetracórica quiral, [3,4,3] + , () se genera mediante 3 de 6 rotaciones: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 y S 0,3 . Grupo iónico disminuido [3,4,3 + ], () se genera por la reflexión R 0 y las rotaciones S 1,2 y S 2,3 . Una rotación doble de 12 veces se genera por W 0,1,2,3 , el producto de las 4 reflexiones.
El grupo [[3,4,3]] extiende [3,4,3] mediante una rotación doble, T, de orden de duplicación hasta 2304.
La simetría hipericosaédrica, [5,3,3], orden 14400,. Las matrices generadoras de reflexión son R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 5 = (R 1 ×R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 0 ×R 3 ) 2 =(R 1 ×R 3 ) 2 =Identidad. [5,3,3] + () se genera mediante 3 rotaciones: S 0,1 = R 0 ×R 1 , S 1,2 = R 1 ×R 2 , S 2,3 = R 2 ×R 3 , etc.
El grupo E8 de Coxeter, [3 4,2,1 ],, tiene 8 nodos espejo, orden 696729600 (192x10!). E7 y E6, [3 3,2,1 ],, y [3 2,2,1 ],se puede construir ignorando el primer espejo o los dos primeros espejos respectivamente.
Las matrices afines se representan agregando una fila y una columna adicionales, siendo la última fila cero excepto la última entrada 1. La última columna representa un vector de traducción.
El grupo afín [∞],, puede darse mediante dos matrices de reflexión, x=0 y x=1.
El grupo afín [4,4],, (p4m), se puede dar mediante tres matrices de reflexión, reflexiones a través del eje x (y=0), una diagonal (x=y) y la reflexión afín a través de la línea (x=1). [4,4] + () (p4) se genera por S 0,1 S 1,2 , y S 0,2 . [4 + ,4 + ] () (pgg) se genera mediante una rotación doble S 0,2 y una reflexión deslizante (transreflexión) V 0,1,2 . [4 + ,4] () (p4g) se genera por S 0,1 y R 3 . El grupo [(4,4,2 + )] (
) (cmm), se genera por rotación doble S 1,3 y reflexión R 2 .
El grupo afín [3,6],, (p6m), puede darse mediante tres matrices de reflexión, reflexiones a través del eje x (y=0), la línea y=(√3/2)x, y la línea vertical x=1.
El grupo afín [3 [3] ] se puede construir como un semigrupo de. R 2 se reemplaza por R' 2 = R 2 ×R 1 ×R 2 , representado por el hiperplano: y+(√3/2)x=2. El dominio fundamental es un triángulo equilátero con longitud de arista 2.
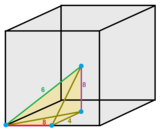
El grupo afín es [4,3,4] (), se puede dar mediante cuatro matrices de reflexión. El espejo R 0 se puede colocar en el plano z=0. El espejo R 1 se puede colocar en el plano y=z. El espejo R 2 se puede colocar en el plano x=y. El espejo R 3 se puede colocar en el plano x=1. [4,3,4] + () se genera por S 0,1 , S 1,2 y S 2,3 .
El grupo extendido [[4,3,4]] duplica el orden del grupo, sumándole una matriz de rotación doble T, con un eje fijo que pasa por los puntos (1,1/2,0) y (1/2,1/2,1/2). Los generadores son {R 0 ,R 1 ,T}. R 2 = T×R 1 ×T y R 3 = T×R 0 ×T.
El grupo [4,3 1,1 ] se puede construir a partir de [4,3,4], calculando [4,3,4,1 + ],, como R' 3 =R 3 ×R 2 ×R 3 , con el nuevo R' 3 como una imagen de R 2 a través de R 3 .
El grupo [3 [4] ] se puede construir a partir de [4,3,4], eliminando el primer y el último espejo, [1 + ,4,3,4,1 + ],, por R' 1 =R 0 ×R 1 ×R 0 y R' 3 =R 3 ×R 2 ×R 3 .
![{\displaystyle \mathbf {A} =\left[{\begin{smallmatrix}1-2a^{2}&-2ab&-2ac\\-2ab&1-2b^{2}&-2bc\\-2ac&-2bc&1-2c^{2}\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da54416016b586c35e295fa5aa6fb4adf99a8c4)