Secuencia de baja discrepancia

Tipo de secuencia matemática

En matemáticas , una secuencia de baja discrepancia es una secuencia con la propiedad de que para todos los valores de N , su subsecuencia x ₁ ,..., x _N tiene una discrepancia baja .

En términos generales, la discrepancia de una secuencia es baja si la proporción de puntos de la secuencia que caen en un conjunto arbitrario B es casi proporcional a la medida de B , como sucedería en promedio (pero no para muestras particulares) en el caso de una secuencia equidistribuida . Las definiciones específicas de discrepancia difieren con respecto a la elección de B ( hiperesferas , hipercubos , etc.) y cómo se calcula (normalmente normalizada) y se combina (normalmente tomando el peor valor) la discrepancia para cada B.

Las secuencias de baja discrepancia también se denominan secuencias cuasi aleatorias , debido a su uso común como reemplazo de números aleatorios uniformemente distribuidos . El modificador "cuasi" se utiliza para indicar más claramente que los valores de una secuencia de baja discrepancia no son aleatorios ni pseudoaleatorios , pero dichas secuencias comparten algunas propiedades de las variables aleatorias y en ciertas aplicaciones, como el método cuasi-Monte Carlo, su menor discrepancia. es una ventaja importante.

Aplicaciones

Error en la curtosis estimada en función del número de puntos de datos. 'Cuasi aleatorio aditivo' da el error máximo cuando c  = ( √ 5  − 1)/2. 'Aleatorio' proporciona el error promedio de seis ejecuciones de números aleatorios, donde el promedio se toma para reducir la magnitud de las fluctuaciones salvajes.

Los números cuasi aleatorios tienen la ventaja sobre los números aleatorios puros de que cubren el dominio de interés de forma rápida y uniforme.

Dos aplicaciones útiles son encontrar la función característica de una función de densidad de probabilidad y encontrar la función derivada de una función determinista con una pequeña cantidad de ruido. Los números cuasi aleatorios permiten calcular muy rápidamente momentos de orden superior con gran precisión.

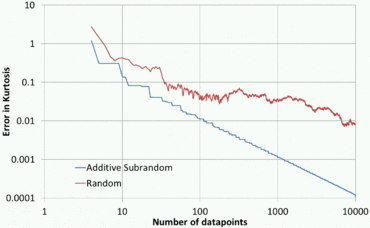
Las aplicaciones que no implican clasificación serían encontrar la media , la desviación estándar , la asimetría y la curtosis de una distribución estadística, y encontrar los máximos y mínimos integrales y globales de funciones deterministas difíciles. Los números cuasi aleatorios también se pueden utilizar para proporcionar puntos de partida para algoritmos deterministas que solo funcionan localmente, como la iteración de Newton-Raphson .

Los números cuasi aleatorios también se pueden combinar con algoritmos de búsqueda. Con un algoritmo de búsqueda, se pueden utilizar números cuasi aleatorios para encontrar la moda , la mediana , los intervalos de confianza y la distribución acumulativa de una distribución estadística, y todos los mínimos locales y todas las soluciones de funciones deterministas.

Secuencias de baja discrepancia en integración numérica.

Se pueden formular varios métodos de integración numérica para aproximar la integral de una función f en algún intervalo, por ejemplo, [0,1], como el promedio de la función evaluada en un conjunto { x ₁ , ..., x _N } en ese intervalo:

${\displaystyle \int _{0}^{1}f(u)\,du\approx {\frac {1}{N}}\,\sum _{i=1}^{N}f(x_{i}).}$

Si los puntos se eligen como x _i = i / N , esta es la regla del rectángulo . Si los puntos se eligen para que se distribuyan aleatoriamente (o pseudoaleatoriamente ), este es el método de Monte Carlo . Si los puntos se eligen como elementos de una secuencia de baja discrepancia, este es el método cuasi-Montecarlo . Un resultado notable, la desigualdad de Koksma-Hlawka (que se indica a continuación), muestra que el error de dicho método puede estar acotado por el producto de dos términos, uno de los cuales depende sólo de f y el otro es la discrepancia del conjunto. { x ₁ , ..., x _norte }.

Es conveniente construir el conjunto { x ₁ , ..., x _N } de tal manera que si se construye un conjunto con N +1 elementos, no sea necesario volver a calcular los N elementos anteriores. La regla del rectángulo utiliza conjuntos de puntos que tienen poca discrepancia, pero en general los elementos deben recalcularse si N aumenta. No es necesario volver a calcular los elementos en el método aleatorio de Monte Carlo si se aumenta N , pero los conjuntos de puntos no tienen una discrepancia mínima. Al utilizar secuencias de baja discrepancia, nuestro objetivo es lograr una baja discrepancia y que no sea necesario volver a calcular, pero en realidad las secuencias de baja discrepancia solo pueden ser incrementalmente buenas en cuanto a discrepancia si no permitimos ningún nuevo cálculo.

Definición de discrepancia

La discrepancia de un conjunto P = { x ₁ , ..., x _N } se define, utilizando la notación de Niederreiter , como

${\displaystyle D_{N}(P)=\sup _{B\in J}\left|{\frac {A(B;P)}{N}}-\lambda _{s}(B)\right|}$

donde λ _s es la medida de Lebesgue s -dimensional , A ( B ; P ) es el número de puntos en P que caen en B , y J es el conjunto de intervalos o cajas s -dimensionales de la forma

${\displaystyle \prod _{i=1}^{s}[a_{i},b_{i})=\{\mathbf {x} \in \mathbf {R} ^{s}:a_{i}\leq x_{i}<b_{i}\}\,}$

dónde . ${\displaystyle 0\leq a_{i}<b_{i}\leq 1}$

La discrepancia de estrellas D ^* _N ( P ) se define de manera similar, excepto que el supremo se toma sobre el conjunto J ^* de cajas rectangulares de la forma

${\displaystyle \prod _{i=1}^{s}[0,u_{i})}$

donde u _i está en el intervalo semiabierto [0, 1).

Los dos están relacionados por

${\displaystyle D_{N}^{*}\leq D_{N}\leq 2^{s}D_{N}^{*}.\,}$

Nota: Con estas definiciones, la discrepancia representa el peor de los casos o la desviación máxima de densidad de puntos de un conjunto uniforme. Sin embargo, también son significativas otras medidas de error, lo que lleva a otras definiciones y medidas de variación. Por ejemplo, la discrepancia L2 o la discrepancia L2 centrada modificada también se utilizan intensivamente para comparar la calidad de conjuntos de puntos uniformes. Ambos son mucho más fáciles de calcular para N y s grandes.

La desigualdad Koksma-Hlawka

Sea Ī ^s el cubo unitario de s dimensiones, Ī ^s = [0, 1] × ... × [0, 1]. Sea f una variación acotada V ( f ) sobre Ī ^s en el sentido de Hardy y Krause. Entonces para cualquier x ₁ , ..., x _N en I ^s = [0, 1) × ... × [0, 1),

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|\leq V(f)\,D_{N}^{*}(x_{1},\ldots ,x_{N}).}$

La desigualdad de Koksma - Hlawka es aguda en el siguiente sentido: para cualquier conjunto de puntos { x ₁ ,..., x _N } en I ^s y any , existe una función f con variación acotada y V ( f ) = 1 tal que ${\displaystyle \varepsilon >0}$

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|>D_{N}^{*}(x_{1},\ldots ,x_{N})-\varepsilon .}$

Por tanto, la calidad de una regla de integración numérica depende únicamente de la discrepancia D ^* _N ( x ₁ ,..., x _N ).

La fórmula de Hlawka-Zaremba

Dejar . porque escribimos ${\displaystyle D=\{1,2,\ldots ,d\}}$ ${\displaystyle \emptyset \neq u\subseteq D}$

${\displaystyle dx_{u}:=\prod _{j\in u}dx_{j}}$

y denota por el punto obtenido de x reemplazando las coordenadas que no están en u por . Entonces ${\displaystyle (x_{u},1)}$ ${\displaystyle 1}$

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du=\sum _{\emptyset \neq u\subseteq D}(-1)^{|u|}\int _{[0,1]^{|u|}}\operatorname {disc} (x_{u},1){\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\,dx_{u},}$

¿Dónde está la función de discrepancia? ${\displaystyle \operatorname {disc} (z)={\frac {1}{N}}\sum _{i=1}^{N}\prod _{j=1}^{d}1_{[0,z_{j})}(x_{i,j})-\prod _{j=1}^{d}z_{i}}$

La versión L 2 de la desigualdad de Koksma-Hlawka

Aplicando la desigualdad de Cauchy-Schwarz para integrales y sumas a la identidad de Hlawka-Zaremba, obtenemos una versión de la desigualdad de Koksma-Hlawka: ${\displaystyle L^{2}}$

${\displaystyle \left|{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f(u)\,du\right|\leq \|f\|_{d}\operatorname {disc} _{d}(\{t_{i}\}),}$

dónde

${\displaystyle \operatorname {disc} _{d}(\{t_{i}\})=\left(\sum _{\emptyset \neq u\subseteq D}\int _{[0,1]^{|u|}}\operatorname {disc} (x_{u},1)^{2}\,dx_{u}\right)^{1/2}}$

y

${\displaystyle \|f\|_{d}=\left(\sum _{u\subseteq D}\int _{[0,1]^{|u|}}\left|{\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\right|^{2}dx_{u}\right)^{1/2}.}$

${\displaystyle L^{2}}$La discrepancia tiene una gran importancia práctica porque son posibles cálculos explícitos rápidos para un conjunto de puntos determinado. De esta manera es fácil crear optimizadores de conjuntos de puntos utilizando la discrepancia como criterio. ${\displaystyle L^{2}}$

La desigualdad Erdős-Turán-Koksma

Es computacionalmente difícil encontrar el valor exacto de la discrepancia de conjuntos de puntos grandes. La desigualdad Erdős – Turán – Koksma proporciona un límite superior.

Sean x ₁ ,..., x _N puntos en I ^s y H un entero positivo arbitrario. Entonces

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\leq \left({\frac {3}{2}}\right)^{s}\left({\frac {2}{H+1}}+\sum _{0<\|h\|_{\infty }\leq H}{\frac {1}{r(h)}}\left|{\frac {1}{N}}\sum _{n=1}^{N}e^{2\pi i\langle h,x_{n}\rangle }\right|\right)}$

dónde

${\displaystyle r(h)=\prod _{i=1}^{s}\max\{1,|h_{i}|\}\quad {\mbox{for}}\quad h=(h_{1},\ldots ,h_{s})\in \mathbb {Z} ^{s}.}$

Las principales conjeturas

Conjetura 1. Existe una constante c _s que depende únicamente de la dimensión s , tal que

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq c_{s}{\frac {(\ln N)^{s-1}}{N}}}$

para cualquier conjunto de puntos finitos { x ₁ ,..., x _N }.

Conjetura 2. Existe una constante c ^' _s que depende sólo de s , tal que

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq c'_{s}{\frac {(\ln N)^{s}}{N}}}$

para un número infinito de N para cualquier secuencia infinita x ₁ , x ₂ , x ₃ ,....

Estas conjeturas son equivalentes. WM Schmidt los demostró para s ≤ 2. En dimensiones superiores, el problema correspondiente todavía está abierto. Los límites inferiores más conocidos se deben a Michael Lacey y sus colaboradores.

límites inferiores

Sea s  = 1. Entonces

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq {\frac {1}{2N}}}$

para cualquier conjunto de puntos finitos { x ₁ , ...,  x _N }.

Sea s  = 2. WM Schmidt demostró que para cualquier conjunto de puntos finitos { x ₁ , ...,  x _N },

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq C{\frac {\log N}{N}}}$

dónde

${\displaystyle C=\max _{a\geq 3}{\frac {1}{16}}{\frac {a-2}{a\log a}}=0.023335\dots .}$

Para dimensiones arbitrarias s  > 1, KF Roth demostró que

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq {\frac {1}{2^{4s}}}{\frac {1}{((s-1)\log 2)^{\frac {s-1}{2}}}}{\frac {\log ^{\frac {s-1}{2}}N}{N}}}$

para cualquier conjunto de puntos finitos { x ₁ , ...,  x _N }. Jozef Beck ^[1] estableció una mejora logarítmica doble de este resultado en tres dimensiones. Esto fue mejorado por D. Bilyk y MT Lacey a una potencia de un solo logaritmo. La cota más conocida para s  > 2 se debe a D. Bilyk, MT Lacey y A. Vagharshakyan. ^[2] Para s  > 2 existe un t  > 0 tal que

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\geq t{\frac {\log ^{{\frac {s-1}{2}}+t}N}{N}}}$

para cualquier conjunto de puntos finitos { x ₁ , ...,  x _N }.

Construcción de secuencias de baja discrepancia.

Debido a que cualquier distribución de números aleatorios se puede asignar a una distribución uniforme, y los números cuasialeatorios se asignan de la misma manera, este artículo solo se ocupa de la generación de números cuasialeatorios en una distribución uniforme multidimensional.

Hay construcciones de secuencias conocidas tales que

${\displaystyle D_{N}^{*}(x_{1},\ldots ,x_{N})\leq C{\frac {(\ln N)^{s}}{N}}.}$

donde C es una determinada constante, dependiendo de la secuencia. Después de la Conjetura 2, se cree que estas secuencias tienen el mejor orden de convergencia posible. Los ejemplos siguientes son la secuencia de van der Corput , las secuencias de Halton y las secuencias de Sobol . Una limitación general es que los métodos de construcción normalmente sólo pueden garantizar el orden de convergencia. En la práctica, sólo se puede lograr una discrepancia baja si N es lo suficientemente grande, y para s dados grandes, este N mínimo puede ser muy grande. Esto significa que ejecutar un análisis Monte-Carlo con, por ejemplo, s=20 variables y N=1000 puntos desde un generador de secuencia de baja discrepancia puede ofrecer sólo una mejora mínima en la precisión ^{[ cita necesaria ]} .

Números al azar

Se pueden generar secuencias de números cuasi aleatorios a partir de números aleatorios imponiendo una correlación negativa a esos números aleatorios. Una forma de hacer esto es comenzar con un conjunto de números aleatorios y construir números cuasi aleatorios que sean uniformes usando : ${\displaystyle r_{i}}$ ${\displaystyle [0,0.5)}$ ${\displaystyle s_{i}}$ ${\displaystyle [0,1)}$

${\displaystyle s_{i}=r_{i}}$para pares e impares . ${\displaystyle i}$ ${\displaystyle s_{i}=0.5+r_{i}}$ ${\displaystyle i}$

Una segunda forma de hacerlo con los números aleatorios iniciales es construir un paseo aleatorio con un desplazamiento de 0,5 como en:

${\displaystyle s_{i}=s_{i-1}+0.5+r_{i}{\pmod {1}}.\,}$

Es decir, tome el número cuasi aleatorio anterior, sume 0,5 y el número aleatorio, y tome el resultado módulo  1.

Para más de una dimensión, se pueden utilizar cuadrados latinos de la dimensión adecuada para proporcionar compensaciones y garantizar que todo el dominio quede cubierto de manera uniforme.

Cobertura del cuadrado unitario. A la izquierda para números cuasi aleatorios aditivos con c  = 0,5545497..., 0,308517... A la derecha para números aleatorios. De arriba a abajo. 10, 100, 1000, 10000 puntos.

recurrencia aditiva

Para cualquier irracional , la secuencia ${\displaystyle \alpha }$

${\displaystyle s_{n}=\{s_{0}+n\alpha \}}$

tiene discrepancia que tiende a . Tenga en cuenta que la secuencia se puede definir de forma recursiva mediante ${\displaystyle 1/N}$

${\displaystyle s_{n+1}=(s_{n}+\alpha ){\bmod {1}}\;.}$

Un buen valor de da una discrepancia menor que una secuencia de números aleatorios uniformes independientes. ${\displaystyle \alpha }$

La discrepancia puede estar limitada por el exponente de aproximación de . Si el exponente de aproximación es , entonces para cualquiera , se cumple el siguiente límite: ^[3] ${\displaystyle \alpha }$ ${\displaystyle \mu }$ ${\displaystyle \varepsilon >0}$

${\displaystyle D_{N}((s_{n}))=O_{\varepsilon }(N^{-1/(\mu -1)+\varepsilon }).}$

Según el teorema de Thue-Siegel-Roth , el exponente de aproximación de cualquier número algebraico irracional es 2, dando un límite de lo anterior. ${\displaystyle N^{-1+\varepsilon }}$

La relación de recurrencia anterior es similar a la relación de recurrencia utilizada por un generador congruente lineal , un generador de números pseudoaleatorios de mala calidad: ^[4]

${\displaystyle r_{i}=(ar_{i-1}+c){\bmod {m}}}$

Para la recurrencia aditiva de baja discrepancia anterior, se elige que a y m sean 1. Sin embargo, tenga en cuenta que esto no generará números aleatorios independientes, por lo que no debe usarse para propósitos que requieran independencia.

El valor de con menor discrepancia es la parte fraccionaria de la proporción áurea : ^[5] ${\displaystyle c}$

${\displaystyle c={\frac {{\sqrt {5}}-1}{2}}=\varphi -1\approx 0.618034.}$

Otro valor casi tan bueno es la parte fraccionaria de la proporción de plata , que es la parte fraccionaria de la raíz cuadrada de 2:

${\displaystyle c={\sqrt {2}}-1\approx 0.414214.\,}$

En más de una dimensión, se necesitan números cuasi aleatorios separados para cada dimensión. Un conjunto conveniente de valores que se utilizan son las raíces cuadradas de números primos desde dos en adelante, todos tomados en módulo 1:

${\displaystyle c={\sqrt {2}},{\sqrt {3}},{\sqrt {5}},{\sqrt {7}},{\sqrt {11}},\ldots \,}$

Sin embargo, se ha demostrado que un conjunto de valores basados ​​en la proporción áurea generalizada produce puntos distribuidos de manera más uniforme. ^[6]

La lista de generadores de números pseudoaleatorios enumera métodos para generar números pseudoaleatorios independientes. Nota: En algunas dimensiones, la recurrencia recursiva conduce a conjuntos uniformes de buena calidad, pero para s más grandes (como s>8) otros generadores de conjuntos de puntos pueden ofrecer discrepancias mucho menores.

secuencia de van der Corput

Dejar

${\displaystyle n=\sum _{k=0}^{L-1}d_{k}(n)b^{k}}$

sea ​​la representación b -aria del entero positivo n ≥ 1, es decir, 0 ≤ d _k ( n ) < b . Colocar

${\displaystyle g_{b}(n)=\sum _{k=0}^{L-1}d_{k}(n)b^{-k-1}.}$

Entonces existe una constante C que depende sólo de b tal que ( g _b ( n )) _{n ≥ 1} satisface

${\displaystyle D_{N}^{*}(g_{b}(1),\dots ,g_{b}(N))\leq C{\frac {\log N}{N}},}$

donde D ^* _N es la discrepancia de estrellas .

secuencia de halton

Primeros 256 puntos de la secuencia de Halton (2,3)

La secuencia de Halton es una generalización natural de la secuencia de van der Corput a dimensiones superiores. Sea s una dimensión arbitraria y b ₁ , ..., b _s sean enteros coprimos arbitrarios mayores que 1. Defina

${\displaystyle x(n)=(g_{b_{1}}(n),\dots ,g_{b_{s}}(n)).}$

Entonces hay una constante C que depende sólo de b ₁ , ..., b _s , tal que la secuencia { x ( n )} _{n ≥1} es una secuencia s -dimensional con

${\displaystyle D_{N}^{*}(x(1),\dots ,x(N))\leq C'{\frac {(\log N)^{s}}{N}}.}$

Conjunto Hammersley

Juego Hammersley 2D de talla 256.

Sean b ₁ ,..., b _{s −1} enteros positivos coprimos mayores que 1. Para s y N dados , el conjunto Hammersley s -dimensional de tamaño N está definido por ^[7]

${\displaystyle x(n)=\left(g_{b_{1}}(n),\dots ,g_{b_{s-1}}(n),{\frac {n}{N}}\right)}$

para norte = 1, ..., norte . Entonces

${\displaystyle D_{N}^{*}(x(1),\dots ,x(N))\leq C{\frac {(\log N)^{s-1}}{N}}}$

donde C es una constante que depende sólo de b ₁ , ..., b _{s −1} . Nota: Las fórmulas muestran que el conjunto de Hammersley es en realidad la secuencia de Halton, pero obtenemos una dimensión más gratis agregando un barrido lineal. Esto sólo es posible si N se conoce de antemano. Un conjunto lineal es también el conjunto con la menor discrepancia unidimensional posible en general. Desafortunadamente, para dimensiones superiores no se conocen tales "conjuntos de registros de discrepancia". Para s  = 2, la mayoría de los generadores de conjuntos de puntos de baja discrepancia ofrecen al menos discrepancias casi óptimas.

secuencia de sobol

La variante Antonov-Saleev de la secuencia de Sobol genera números entre cero y uno directamente como fracciones binarias de longitud , a partir de un conjunto de fracciones binarias especiales, llamadas números de dirección. Los bits del código Gray de , , se utilizan para seleccionar números de dirección. Para obtener el valor de la secuencia de Sobol, tome el valor exclusivo o binario del código Gray con el número de dirección apropiado. El número de dimensiones requeridas afecta la elección de . ${\displaystyle w}$ ${\displaystyle w}$ ${\displaystyle V_{i},i=1,2,\dots ,w}$ ${\displaystyle i}$ ${\displaystyle G(i)}$ ${\displaystyle s_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}}$

Muestreo de disco de Poisson

El muestreo de disco de Poisson es popular en los videojuegos para colocar rápidamente objetos de una manera que parezca aleatoria pero garantiza que cada dos puntos estén separados por al menos la distancia mínima especificada. ^[8] Esto no garantiza una discrepancia baja (como, por ejemplo, Sobol'), pero al menos una discrepancia significativamente menor que el muestreo aleatorio puro. El objetivo de estos patrones de muestreo se basa en el análisis de frecuencia y no en la discrepancia, un tipo de patrones llamados "ruido azul".

Ejemplos gráficos

Los puntos que se representan a continuación son los primeros 100, 1000 y 10000 elementos de una secuencia del tipo Sobol'. A modo de comparación, también se muestran 10.000 elementos de una secuencia de puntos pseudoaleatorios. La secuencia de baja discrepancia fue generada por el algoritmo TOMS 659. ^[9] Una implementación del algoritmo en Fortran está disponible en Netlib .

Los primeros 100 puntos de una secuencia de baja discrepancia del tipo Sobol' .

Los primeros 1000 puntos en la misma secuencia. Estos 1000 comprenden los 100 primeros, con 900 puntos más.

Los primeros 10000 puntos en la misma secuencia. Estos 10.000 comprenden los primeros 1.000, con 9.000 puntos más.

A modo de comparación, aquí están los primeros 10000 puntos de una secuencia de números pseudoaleatorios distribuidos uniformemente. Son evidentes regiones de mayor y menor densidad.

Ver también

• Teoría de la discrepancia
• Cadena de Markov Montecarlo
• Método cuasi-Montecarlo
• Cuadrícula escasa
• Muestreo sistemático

Notas

1. Beck, József (1989). "Un teorema bidimensional de van Aardenne-Ehrenfest en irregularidades de distribución". Composición Matemática . 72 (3): 269–339. SEÑOR  1032337. S2CID  125940424. Zbl  0691.10041.
2. Bilyk, Dmitriy; Lacey, Michael T.; Vagharshakyan, Armen (2008). "Sobre la desigualdad de la pequeña bola en todas las dimensiones". Revista de análisis funcional . 254 (9): 2470–2502. arXiv : 0705.4619 . doi : 10.1016/j.jfa.2007.09.010 . S2CID  14234006.
3. Kuipers y Niederreiter 2005, pág. 123
4. Knuth, Donald E. "Capítulo 3: Números aleatorios". El arte de la programación informática . vol. 2.
5. Skarupke, Malta (16 de junio de 2018). "Fibonacci Hashing: la optimización que el mundo olvidó". Una propiedad de la Proporción Áurea es que puedes usarla para subdividir cualquier rango de manera aproximadamente uniforme... si no sabes de antemano cuántos pasos vas a dar
6. Roberts, Martín (2018). "La eficacia irrazonable de las secuencias cuasi aleatorias".
7. Hammersley, JM; Handscomb, CC (1964). Métodos de Montecarlo . doi :10.1007/978-94-009-5819-7. ISBN 978-94-009-5821-0.
8. Herman Tulleken.Tulleken, Herman (marzo de 2008). "Muestreo de disco de Poisson". Dev.Mag . Núm. 21, págs. 21-25.
9. Bratley, Pablo; Zorro, Bennett L. (1988). "Algoritmo 659". Transacciones ACM sobre software matemático . 14 : 88-100. doi : 10.1145/42288.214372 . S2CID  17325779.

Referencias

• Dick, José; Pillichshammer, Friedrich (2010). Redes y secuencias digitales: teoría de la discrepancia e integración cuasi-Monte Carlo . ISBN 978-0-521-19159-3.
• Kuipers, L.; Niederreiter, H. (2005), Distribución uniforme de secuencias , Publicaciones de Dover , ISBN 0-486-45019-8
• Harald Niederreiter (1992). Métodos de generación de números aleatorios y cuasi-Monte Carlo . Sociedad de Matemática Industrial y Aplicada. ISBN 0-89871-295-5.
• Drmota, Michael; Tichy, Robert F. (1997). Secuencias, Discrepancias y Aplicaciones . Apuntes de clases de matemáticas. vol. 1651. Saltador. ISBN 3-540-62606-9.
• Prensa, William H.; Flannery, Brian P.; Teukolsky, Saúl A.; Vetterling, William T. (1992). Recetas numéricas en C (2ª ed.). Prensa de la Universidad de Cambridge. consulte la Sección 7.7 para una discusión menos técnica sobre secuencias de baja discrepancia. ISBN 0-521-43108-5.

enlaces externos

• Algoritmos recopilados del ACM (consulte los algoritmos 647, 659 y 738).
• Secuencias cuasi aleatorias de la biblioteca científica GNU
• Muestreo cuasi aleatorio sujeto a restricciones en FinancialMathematics.Com
• Generador C++ de secuencia de Sobol
• Referencia de la API de SciPy QMC: scipy.stats.qmc