Número cuadrado centrado

Número figurado centrado que da la cantidad de puntos en un cuadrado con un punto en el centro.

En la teoría elemental de números , un número cuadrado centrado es un número figurado centrado que da el número de puntos en un cuadrado con un punto en el centro y todos los demás puntos que rodean el punto central en capas cuadradas sucesivas. Es decir, cada número cuadrado centrado es igual al número de puntos dentro de una distancia de una manzana de la ciudad dada desde el punto central en un entramado cuadrado regular . Si bien los números cuadrados centrados, como los números figurados en general, tienen pocas aplicaciones prácticas directas, si es que tienen alguna, a veces se los estudia en matemáticas recreativas por sus elegantes propiedades geométricas y aritméticas.

Las cifras correspondientes a los primeros cuatro números cuadrados centrados se muestran a continuación:

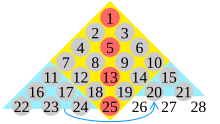
Cada número cuadrado centrado es la suma de cuadrados sucesivos. Ejemplo: como se muestra en la siguiente figura del triángulo de Floyd , 25 es un número cuadrado centrado, y es la suma del cuadrado 16 (rombo amarillo formado al cortar un cuadrado) y del cuadrado siguiente más pequeño, 9 (suma de dos triángulos azules):

Los números cuadrados centrados (en rojo) están en el centro de las filas impares del triángulo de Floyd.

Relaciones con otros números figurados

Sea C _{k , n} el número k -gonal centrado en el n º . El número cuadrado centrado en el n º viene dado por la fórmula:

${\displaystyle C_{4,n}=n^{2}+(n-1)^{2}.}$

Es decir, el n- ésimo número cuadrado centrado es la suma del n -ésimo y el ( n – 1)-ésimo número cuadrado . El siguiente patrón demuestra esta fórmula:

La fórmula también se puede expresar como:

${\displaystyle C_{4,n}={\frac {(2n-1)^{2}+1}{2}}.}$

Es decir, el n -ésimo número cuadrado centrado es la mitad del n -ésimo número cuadrado impar más 1, como se ilustra a continuación:

Como todos los números poligonales centrados , los números cuadrados centrados también se pueden expresar en términos de números triangulares :

${\displaystyle C_{4,n}=1+4\ T_{n-1}=1+2{n(n-1)},}$

dónde

${\displaystyle T_{n}={\frac {n(n+1)}{2}}={\binom {n+1}{2}}}$

es el n- ésimo número triangular. Esto se puede ver fácilmente quitando el punto central y dividiendo el resto de la figura en cuatro triángulos, como se muestra a continuación:

La diferencia entre dos números octaédricos consecutivos es un número cuadrado centrado (Conway y Guy, p.50).

Otra forma en que se pueden expresar los números cuadrados centrados es:

${\displaystyle C_{4,n}=1+4\dim(SO(n)),}$

dónde

${\displaystyle \dim(SO(n))={\frac {n(n-1)}{2}}.}$

Otra forma en que se pueden expresar los números cuadrados centrados es en términos de números triangulares centrados :

${\displaystyle C_{4,n}={\frac {4C_{3,n}-1}{3}},}$

dónde

${\displaystyle C_{3,n}=1+3{\frac {n(n-1)}{2}}.}$

Lista de números cuadrados centrados

Los primeros números cuadrados centrados ( C _{4, n} < 4500) son:

1 , 5 , 13 , 25 , 41 , 61 , 85 , 113 , 145 , 181 , 221 , 265, 313 , 365 , 421, 481, 545, 613, 685, 761, 841, 925, 1013, 05, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, … (secuencia A001844 en la OEIS ).

Propiedades

Todos los números cuadrados centrados son impares, y en base 10 se puede observar que el dígito de las unidades sigue el patrón 1-5-3-5-1.

Todos los números cuadrados centrados y sus divisores tienen un resto de 1 cuando se dividen por 4. Por lo tanto, todos los números cuadrados centrados y sus divisores terminan con el dígito 1 o 5 en base 6 , 8 y 12 .

Todo número cuadrado centrado excepto el 1 es la hipotenusa de una terna pitagórica (3-4- 5 , 5-12- 13 , 7-24- 25 , ...). Esta es exactamente la secuencia de ternas pitagóricas donde los dos lados más largos difieren en 1. (Ejemplo: 5 ² + 12 ² = 13 ² .)

Esto no debe confundirse con la relación ( n – 1) ² + n ² = C _{4, n} . (Ejemplo: 2 ² + 3 ² = 13 .)

Función generadora

La función generadora que da los números cuadrados centrados es:

${\displaystyle {\frac {(x+1)^{2}}{(1-x)^{3}}}=1+5x+13x^{2}+25x^{3}+41x^{4}+~...~.}$

Referencias

• Alfred, U. (1962), " n y n + 1 enteros consecutivos con sumas de cuadrados iguales", Mathematics Magazine , 35 (3): 155–164, doi :10.1080/0025570X.1962.11975326, JSTOR  2688938, MR  1571197.
• Apostol, Tom M. (1976), Introducción a la teoría analítica de números , Textos de pregrado en matemáticas, Nueva York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR  0434929, Zbl  0335.10001.
• Beiler, AH (1964), Recreaciones en la teoría de números , Nueva York: Dover, pág. 125.
• Conway, John H. ; Guy, Richard K. (1996), El libro de los números, Nueva York: Copernicus, págs. 41–42, ISBN 0-387-97993-X, Sr.  1411676.