
Un motor térmico de Carnot [2] es un motor térmico teórico que opera según el ciclo de Carnot . El modelo básico de este motor fue desarrollado por Nicolas Léonard Sadi Carnot en 1824. El modelo del motor de Carnot fue ampliado gráficamente por Benoît Paul Émile Clapeyron en 1834 y explorado matemáticamente por Rudolf Clausius en 1857, trabajo que condujo al concepto termodinámico fundamental de entropía . El motor de Carnot es el motor térmico más eficiente que es teóricamente posible. [3] La eficiencia depende únicamente de las temperaturas absolutas de los depósitos de calor caliente y frío entre los que opera.
Un motor térmico actúa transfiriendo energía de una región cálida a una región fría del espacio y, en el proceso, convirtiendo parte de esa energía en trabajo mecánico . El ciclo también puede invertirse. El sistema puede ser sometido a una fuerza externa y, en el proceso, puede transferir energía térmica de un sistema más frío a uno más cálido, actuando así como un refrigerador o una bomba de calor en lugar de un motor térmico.
Todo sistema termodinámico existe en un estado particular . Un ciclo termodinámico ocurre cuando un sistema pasa por una serie de estados diferentes y finalmente regresa a su estado inicial. En el proceso de pasar por este ciclo, el sistema puede realizar trabajo sobre su entorno, actuando así como un motor térmico.
El motor de Carnot es un concepto teórico que resulta útil para explorar los límites de eficiencia de otros motores térmicos. Sin embargo, construir un motor de Carnot real sería completamente impráctico.
En el diagrama adyacente, de la obra de Carnot de 1824, Reflexiones sobre la fuerza motriz del fuego , [4] hay "dos cuerpos A y B , mantenidos cada uno a una temperatura constante, siendo la de A más alta que la de B. Estos dos cuerpos a los que podemos dar, o de los que podemos quitar el calor sin hacer que varíen sus temperaturas, ejercen las funciones de dos depósitos ilimitados de calor . Llamaremos al primero horno y al segundo refrigerador". [5] Carnot explica luego cómo podemos obtener fuerza motriz , es decir, "trabajo", al transportar una cierta cantidad de calor del cuerpo A al cuerpo B. También actúa como un enfriador y, por lo tanto, también puede actuar como un refrigerador.

La imagen anterior muestra el diagrama original de pistón y cilindro utilizado por Carnot al hablar de su motor ideal. La figura de la derecha muestra un diagrama de bloques de un motor térmico genérico, como el motor de Carnot. En el diagrama, el "cuerpo de trabajo" (sistema), un término introducido por Clausius en 1850, puede ser cualquier cuerpo de fluido o vapor a través del cual se puede introducir o transmitir calor Q para producir trabajo. Carnot había postulado que el cuerpo de fluido podría ser cualquier sustancia capaz de expandirse, como vapor de agua, vapor de alcohol, vapor de mercurio, un gas permanente, aire, etc. Aunque en esos primeros años, los motores venían en varias configuraciones, típicamente Q H era suministrado por una caldera, en la que se hervía agua sobre un horno; Q C era típicamente eliminado por una corriente de agua fría que fluía en forma de un condensador ubicado en una parte separada del motor. El trabajo de salida, W , se transmite por el movimiento del pistón cuando se usa para hacer girar un brazo de manivela, que a su vez se usaba típicamente para impulsar una polea para sacar agua de las minas de sal inundadas. Carnot definió el trabajo como "peso levantado a través de una altura".
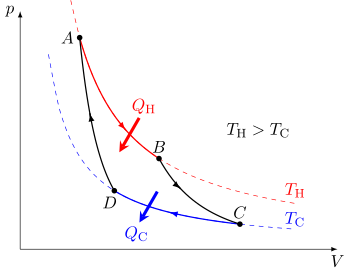
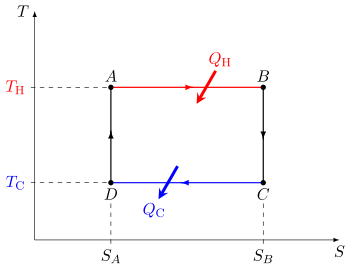
El ciclo de Carnot cuando actúa como motor térmico consta de los siguientes pasos:

El teorema de Carnot es una declaración formal de este hecho: ningún motor que funcione entre dos depósitos de calor puede ser más eficiente que un motor de Carnot que funcione entre los mismos depósitos.
Esta máxima eficiencia η I se define como arriba:
Un corolario del teorema de Carnot establece que: todos los motores reversibles que funcionan entre los mismos depósitos de calor son igualmente eficientes.
Se demuestra fácilmente que la eficiencia η es máxima cuando todo el proceso cíclico es un proceso reversible . Esto significa que la entropía total del sistema y del entorno (las entropías del horno caliente, el "fluido de trabajo" del motor térmico y el disipador frío) permanece constante cuando el "fluido de trabajo" completa un ciclo y vuelve a su estado original. (En el caso general y más realista de un proceso irreversible, la entropía total de este sistema combinado aumentaría).
Como el "fluido de trabajo" vuelve al mismo estado después de un ciclo y la entropía del sistema es una función de estado, el cambio de entropía del sistema del "fluido de trabajo" es 0. Por lo tanto, implica que el cambio de entropía total del horno y el sumidero es cero, para que el proceso sea reversible y la eficiencia del motor sea máxima. Esta derivación se lleva a cabo en la siguiente sección.
El coeficiente de rendimiento (COP) del motor térmico es el recíproco de su eficiencia.
En el caso de un motor térmico real, el proceso termodinámico total es generalmente irreversible. El fluido de trabajo vuelve a su estado inicial después de un ciclo y, por lo tanto, el cambio de entropía del sistema de fluido es cero, pero la suma de los cambios de entropía en el depósito caliente y frío en este proceso cíclico es mayor que cero.
La energía interna del fluido también es una variable de estado, por lo que su cambio total en un ciclo es 0. Por lo tanto, el trabajo total realizado por el sistema W es igual al calor neto introducido en el sistema, la suma de > 0 absorbido y el calor residual < 0 emitido: [6]
En los motores reales, las etapas 1 y 3 del ciclo de Carnot, en las que el calor es absorbido por el "fluido de trabajo" del depósito caliente y liberado por éste al depósito frío, respectivamente, ya no permanecen idealmente reversibles y existe una diferencia de temperatura entre la temperatura del depósito y la temperatura del fluido mientras tiene lugar el intercambio de calor.
Durante la transferencia de calor desde el depósito caliente en al fluido, el fluido tendría una temperatura ligeramente inferior a , y el proceso para el fluido no necesariamente permanecería isotérmico. Sea el cambio de entropía total del fluido en el proceso de absorción de calor.
donde la temperatura del fluido T es siempre ligeramente menor que , en este proceso.
Entonces, obtendríamos:
De manera similar, en el momento de la inyección de calor del fluido al depósito frío se tendría, para la magnitud del cambio de entropía total < 0 del fluido en el proceso de expulsión de calor:
donde, durante este proceso de transferencia de calor al depósito frío, la temperatura del fluido T es siempre ligeramente mayor que .
Aquí sólo hemos considerado la magnitud del cambio de entropía. Dado que el cambio total de entropía del sistema de fluido para el proceso cíclico es 0, debemos tener
Las tres ecuaciones anteriores, a saber (3), (4), (5), sustituidas en (6) dan: [7]
Para [ΔSh ≥ (Qh/Th)] +[ΔSc ≥ (Qc/Tc)] = 0
[ΔSh ≥ (Qh/Th) ] = - [ΔSc ≥ (Qc/Tc)]
= [-ΔSc ≤ (-Qc/Tc) ]
es al menos (Qh/Th) ≤ (-Qc/Tc)
Las ecuaciones ( 2 ) y ( 7 ) se combinan para dar
Para derivar este paso se necesitan dos procesos adiabáticos involucrados para mostrar una propiedad de proceso isentrópico para la relación de los volúmenes cambiantes de dos procesos isotérmicos que son iguales.
Lo más importante es que, dado que los dos procesos adiabáticos son trabajos de volumen sin pérdida de calor, y dado que la relación de los cambios de volumen para estos dos procesos es la misma, los trabajos para estos dos procesos adiabáticos son los mismos con direcciones opuestas entre sí, es decir, una dirección es el trabajo realizado por el sistema y la otra es el trabajo realizado sobre el sistema; por lo tanto, la eficiencia térmica solo se refiere a la cantidad de trabajo realizado por el calor absorbido en comparación con la cantidad de calor absorbido por el sistema.
Por lo tanto, (W/Qh) = (Qh - Qc) / Qh
= 1 - (Qc/Qh)
= 1 - (Tc/Th)
Y, a partir de (7)
(Qh/Th) ≤ (-Qc/Tc) aquí Qc es menor que 0 (libera calor)
(Tc/Th) ≤ (-Qc/Qh)
-(Tc/Th) ≥ (Qc/Qh)
1+ [-(Tc/Th)] ≥ 1+ (Qc/Qh)
1 - (Tc/Th) ≥ (Qh + Qc)/Qh aquí Qc<0,
1 - (Tc/Th) ≥ (Qh - Qc)/Qh
1 - (Tc/Th) ≥ W/Qh
Por eso,
donde es la eficiencia del motor real, y es la eficiencia del motor de Carnot que funciona entre los mismos dos depósitos a las temperaturas y . Para el motor de Carnot, todo el proceso es "reversible" y la ecuación ( 7 ) es una igualdad. Por lo tanto, la eficiencia del motor real es siempre menor que la del motor de Carnot ideal.
La ecuación ( 7 ) significa que la entropía total del sistema y del entorno (el fluido y los dos depósitos) aumenta para el motor real, porque (en un análisis basado en el entorno) la ganancia de entropía del depósito frío cuando fluye hacia él a la temperatura fija es mayor que la pérdida de entropía del depósito caliente cuando lo abandona a su temperatura fija . La desigualdad en la ecuación ( 7 ) es esencialmente el enunciado del teorema de Clausius .
Según el segundo teorema, "La eficiencia de la máquina de Carnot es independiente de la naturaleza de la sustancia activa".
En 1892, Rudolf Diesel patentó un motor de combustión interna inspirado en el motor de Carnot. Diesel sabía que un motor de Carnot era un ideal que no se podía construir, pero pensó que había inventado una aproximación funcional. Su principio no era sólido, pero en su lucha por implementarlo desarrolló un motor Diesel práctico .
El problema conceptual era cómo lograr la expansión isotérmica en un motor de combustión interna, ya que quemar combustible a la temperatura más alta del ciclo solo elevaría aún más la temperatura. La solución patentada de Diesel fue: una vez alcanzada la temperatura más alta simplemente comprimiendo el aire, agregar una pequeña cantidad de combustible a un ritmo controlado, de modo que el calentamiento causado por la quema del combustible se contrarrestara con el enfriamiento causado por la expansión del aire a medida que el pistón se movía. Por lo tanto, todo el calor del combustible se transformaría en trabajo durante la expansión isotérmica, como lo requiere el teorema de Carnot.
Para que la idea funcionara, habría que quemar una pequeña masa de combustible en una enorme masa de aire. Diesel propuso primero un motor que comprimiera el aire a 250 atmósferas a 800 °C (1450 °F) y luego lo calentara a una atmósfera a 20 °C (50 °F). Sin embargo, esto estaba muy por encima de las capacidades tecnológicas de la época, ya que implicaba una relación de compresión de 60:1. Un motor de este tipo, si se hubiera podido construir, habría tenido una eficiencia del 73 % (en contraste, los mejores motores de vapor de su época alcanzaban el 7 %).
En consecuencia, Diesel buscó un compromiso. Calculó que, si reducía la presión máxima a unas menos ambiciosas 90 atmósferas, sacrificaría sólo el 5% de la eficiencia térmica . Buscando apoyo financiero, publicó la "Teoría y construcción de una máquina térmica racional para reemplazar a la máquina de vapor y a todas las máquinas de combustión conocidas actualmente" (1893). Respaldado por la opinión científica, incluido Lord Kelvin , obtuvo el respaldo de Krupp y Maschinenfabrik Augsburg . Se aferró al ciclo de Carnot como símbolo. Pero años de trabajo práctico no lograron lograr un motor de combustión isotérmica, ni podrían haberlo hecho, ya que requiere una cantidad tan enorme de aire que no puede desarrollar suficiente potencia para comprimirlo. Además, la inyección controlada de combustible resultó no ser una tarea fácil.
Aun así, el motor diésel evolucionó lentamente a lo largo de 25 años hasta convertirse en un práctico motor de aire de alta compresión, con su combustible inyectado cerca del final de la carrera de compresión y encendido por el calor de la compresión, capaz en 1969 de alcanzar una eficiencia del 40%. [8]
El motor térmico de Carnot es, en última instancia, una construcción teórica basada en un sistema termodinámico idealizado . A escala humana práctica, el ciclo de Carnot ha demostrado ser un modelo valioso, como en el avance del desarrollo del motor diésel . Sin embargo, a escala macroscópica, las limitaciones impuestas por los supuestos del modelo lo hacen poco práctico y, en última instancia, incapaz de realizar ningún trabajo . [9] Como tal, según el teorema de Carnot , el motor de Carnot puede considerarse el límite teórico de los motores térmicos a escala macroscópica en lugar de cualquier dispositivo práctico que pudiera construirse. [10]
Por ejemplo, para la parte de expansión isotérmica del ciclo de Carnot, las siguientes condiciones infinitesimales deben satisfacerse simultáneamente en cada paso de la expansión: [11]
Requisitos "infinitesimales" como estos (y otros) hacen que el ciclo de Carnot tome una cantidad infinita de tiempo , lo que hace imposible la producción de trabajo. [9]
Otros requisitos prácticos que hacen que el ciclo de Carnot sea poco práctico de realizar incluyen el control fino del gas y el contacto térmico perfecto con el entorno (incluidos los depósitos de alta y baja temperatura). [ cita requerida ]
§90, ecuaciones (39) y (40).
debajo de la ecuación (63).
...desde el motor térmico de Carnot, establecer un límite superior para la eficiencia de un motor térmico es un motor ideal y reversible del cual se debe realizar un solo ciclo en un tiempo infinito, lo que es poco práctico y, por lo tanto, el motor de Carnot tiene potencia cero.
Sin embargo, las fluctuaciones [en la temperatura del yacimiento] hacen que estos motores no sean prácticos.
Episodio 46. El motor de la naturaleza: el motor de Carnot, primera parte, comenzando con simples motores de vapor. El universo mecánico . Caltech – vía YouTube.