Percentil

Estadística que divide un conjunto de datos en 100 partes y lo analiza como porcentaje.

En estadística , un percentil k -ésimo , también conocido como puntuación percentil o percentil , es una puntuación por debajo de la cual cae un porcentaje dado k de puntuaciones en su distribución de frecuencia (definición " exclusiva ") o una puntuación en o por debajo de la cual cae un porcentaje dado (definición " inclusiva "). Los percentiles se expresan en la misma unidad de medida que las puntuaciones de entrada, no en porcentaje ; por ejemplo, si las puntuaciones se refieren al peso humano , los percentiles correspondientes se expresarán en kilogramos o libras. En el límite de un tamaño de muestra infinito , el percentil se aproxima a la función percentil , la inversa de la función de distribución acumulativa .

Los percentiles son un tipo de cuantiles , que se obtienen adoptando una subdivisión en 100 grupos. El percentil 25 también se conoce como primer cuartil ( Q ₁ ), el percentil 50 como mediana o segundo cuartil ( Q ₂ ), y el percentil 75 como tercer cuartil ( Q ₃ ). Por ejemplo, el percentil 50 (mediana) es la puntuación por debajo (o en o por debajo , según la definición) de la cual se encuentran el 50% de las puntuaciones de la distribución.

Una cantidad relacionada es el rango percentil de una puntuación, expresado en porcentaje , que representa la fracción de puntuaciones en su distribución que son menores que ella, una definición exclusiva. Las puntuaciones percentiles y los rangos percentiles se utilizan a menudo en el informe de las puntuaciones de las pruebas de referencia normativa , pero, como se acaba de señalar, no son lo mismo. Para los rangos percentiles, se proporciona una puntuación y se calcula un porcentaje. Los rangos percentiles son exclusivos: si el rango percentil para una puntuación específica es 90%, entonces el 90% de las puntuaciones fueron inferiores. Por el contrario, para los percentiles se proporciona un porcentaje y se determina una puntuación correspondiente, que puede ser exclusiva o inclusiva. La puntuación para un porcentaje específico (p. ej., 90.º) indica una puntuación por debajo de la cual (definición exclusiva) o en o por debajo de la cual (definición inclusiva) caen otras puntuaciones en la distribución.

Definiciones

No existe una definición estándar de percentil; ^{[1] [2] [3]} sin embargo, todas las definiciones arrojan resultados similares cuando el número de observaciones es muy grande y la distribución de probabilidad es continua. ^[4] En el límite, a medida que el tamaño de la muestra se acerca al infinito, el percentil 100 ^p ( 0< p <1) se aproxima a la inversa de la función de distribución acumulativa (CDF) así formada, evaluada en p , ya que p se aproxima a la CDF. Esto puede verse como una consecuencia del teorema de Glivenko-Cantelli . A continuación se dan algunos métodos para calcular los percentiles.

La distribución normal y los percentiles

Representación de la regla de tres sigmas . La zona azul oscuro representa las observaciones dentro de una desviación estándar (σ) a cada lado de la media (μ), lo que representa aproximadamente el 68,3 % de la población. Dos desviaciones estándar de la media (azul oscuro y azul medio) representan aproximadamente el 95,4 %, y tres desviaciones estándar (azul oscuro, medio y claro) representan aproximadamente el 99,7 %.

Los métodos que se dan en la sección de métodos de cálculo (a continuación) son aproximaciones para su uso en estadísticas de muestras pequeñas. En términos generales, para poblaciones muy grandes que siguen una distribución normal , los percentiles a menudo se pueden representar con referencia a un gráfico de curva normal. La distribución normal se traza a lo largo de un eje escalado a desviaciones estándar o unidades sigma ( ). Matemáticamente, la distribución normal se extiende hasta el infinito negativo a la izquierda y el infinito positivo a la derecha. Sin embargo, tenga en cuenta que solo una proporción muy pequeña de individuos en una población quedará fuera del rango de −3 σ a +3 σ . Por ejemplo, con alturas humanas muy pocas personas están por encima del nivel de altura +3 σ . ${\displaystyle \sigma }$

Los percentiles representan el área bajo la curva normal, que aumenta de izquierda a derecha. Cada desviación estándar representa un percentil fijo. Por lo tanto, redondeando a dos decimales, −3 σ es el percentil 0,13, −2 σ el percentil 2,28, −1 σ el percentil 15,87, 0 σ el percentil 50 (tanto la media como la mediana de la distribución), +1 σ el percentil 84,13, +2 σ el percentil 97,72 y +3 σ el percentil 99,87. Esto está relacionado con la regla 68-95-99,7 o regla de las tres sigmas. Téngase en cuenta que, en teoría, el percentil 0 cae en el infinito negativo y el percentil 100 en el infinito positivo, aunque en muchas aplicaciones prácticas, como los resultados de pruebas, se aplican límites inferiores y/o superiores naturales.

Aplicaciones

Cuando los ISP facturan un ancho de banda de Internet "burstable" , el percentil 95 o 98 generalmente elimina el 5 % o 2 % superior de los picos de ancho de banda de cada mes y luego factura según la tarifa más cercana. De esta manera, se ignoran los picos poco frecuentes y se le cobra al cliente de una manera más justa. La razón por la que esta estadística es tan útil para medir el rendimiento de los datos es que brinda una imagen muy precisa del costo del ancho de banda. El percentil 95 indica que el 95 % del tiempo, el uso está por debajo de esta cantidad: por lo tanto, el 5 % restante del tiempo, el uso está por encima de esa cantidad.

Los médicos a menudo utilizan el peso y la altura de los bebés y los niños para evaluar su crecimiento en comparación con los promedios y percentiles nacionales que se encuentran en las tablas de crecimiento .

El percentil 85 de la velocidad del tráfico en una carretera se utiliza a menudo como guía para establecer límites de velocidad y evaluar si dicho límite es demasiado alto o bajo. ^{[5] [6]}

En finanzas, el valor en riesgo es una medida estándar para evaluar (de manera dependiente del modelo) la cantidad por debajo de la cual no se espera que el valor de la cartera caiga dentro de un período de tiempo determinado y dado un valor de confianza.

Métodos de cálculo

Percentiles interpolados y de rango más cercano, exclusivos e inclusivos, para una distribución de 10 puntuaciones

Percentiles interpolados y de rango más cercano, exclusivos e inclusivos, para una distribución de 10 puntuaciones

Existen muchas fórmulas o algoritmos ^[7] para calcular una puntuación percentil. Hyndman y Fan ^[1] identificaron nueve y la mayoría de los programas estadísticos y de hojas de cálculo utilizan uno de los métodos que describen. ^[8] Los algoritmos devuelven el valor de una puntuación que existe en el conjunto de puntuaciones (métodos de rango más cercano) o interpolan entre puntuaciones existentes y son excluyentes o inclusivos.

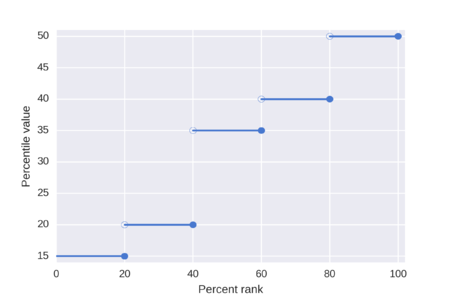
La figura muestra una distribución de 10 puntuaciones, ilustra las puntuaciones percentiles que resultan de estos diferentes algoritmos y sirve como introducción a los ejemplos que se dan a continuación. Los más simples son los métodos de rango más cercano que devuelven una puntuación de la distribución, aunque en comparación con los métodos de interpolación, los resultados pueden ser un poco rudimentarios. La tabla de métodos de rango más cercano muestra los pasos computacionales para los métodos exclusivos e inclusivos.

Los métodos de interpolación, como su nombre lo indica, pueden devolver una puntuación que se encuentra entre las puntuaciones de la distribución. Los algoritmos que utilizan los programas estadísticos suelen utilizar métodos de interpolación, por ejemplo, las funciones percentile.exc y percentile.inc de Microsoft Excel. La tabla Métodos interpolados muestra los pasos de cálculo.

El método del rango más cercano

Los valores de percentil para la lista ordenada {15, 20, 35, 40, 50}

Una definición de percentil, que se da a menudo en los textos, es que el percentil P de una lista de N valores ordenados (ordenados de menor a mayor) es el valor más pequeño de la lista de modo que no más del P por ciento de los datos sea estrictamente menor que el valor y al menos el P por ciento de los datos sea menor o igual a ese valor. Esto se obtiene calculando primero el rango ordinal y luego tomando el valor de la lista ordenada que corresponde a ese rango. El rango ordinal n se calcula utilizando esta fórmula ${\displaystyle (0<P\leq 100)}$

${\displaystyle n=\left\lceil {\frac {P}{100}}\times N\right\rceil .}$

• El uso del método de rango más cercano en listas con menos de 100 valores distintos puede dar como resultado que se utilice el mismo valor para más de un percentil.
• Un percentil calculado utilizando el método de rango más cercano siempre será miembro de la lista ordenada original.
• El percentil 100 se define como el valor más grande en la lista ordenada.

El método de interpolación lineal entre rangos más cercanos

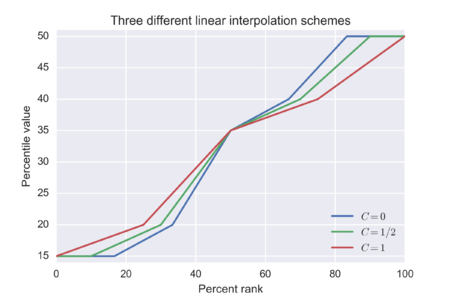
Una alternativa al redondeo utilizada en muchas aplicaciones es utilizar la interpolación lineal entre rangos adyacentes.

Todas las variantes siguientes tienen lo siguiente en común. Dadas las estadísticas de pedidos

${\displaystyle \{v_{i},i=1,2,\ldots ,N:v_{i+1}\geq v_{i},\forall i=1,2,\ldots ,N-1\},}$

Buscamos una función de interpolación lineal que pase por los puntos . Esto se logra simplemente mediante ${\displaystyle (v_{i},i)}$

${\displaystyle v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,}$

donde usa la función floor para representar la parte integral de x positivo , mientras que usa la función mod para representar su parte fraccionaria (el resto después de la división por 1). (Tenga en cuenta que, aunque en el punto final , no está definido, no necesita estarlo porque se multiplica por ). Como podemos ver, x es la versión continua del subíndice i , que interpola linealmente v entre nodos adyacentes. ${\displaystyle \lfloor x\rfloor }$ ${\displaystyle x{\bmod {1}}}$ ${\displaystyle x=N}$ ${\displaystyle v_{\lfloor x\rfloor +1}}$ ${\displaystyle x{\bmod {1}}=0}$

Existen dos formas en las que los enfoques de las variantes difieren. La primera es la relación lineal entre el rango x , el rango porcentual y una constante que es una función del tamaño de la muestra N : ${\displaystyle P=100p}$

${\displaystyle x=f(p,N)=(N+c_{1})p+c_{2}.}$

Existe el requisito adicional de que el punto medio del rango , correspondiente a la mediana , se encuentre en : ${\displaystyle (1,N)}$ ${\displaystyle p=0.5}$

${\displaystyle {\begin{aligned}f(0.5,N)&={\frac {N+c_{1}}{2}}+c_{2}={\frac {N+1}{2}}\\\therefore 2c_{2}+c_{1}&=1\end{aligned}},}$

y nuestra función revisada ahora tiene solo un grado de libertad, luciendo así:

${\displaystyle x=f(p,N)=(N+1-2C)p+C.}$

La segunda forma en que difieren las variantes está en la definición de la función cerca de los márgenes del rango de p : debería producir, o verse forzada a producir, un resultado en el rango , lo que puede significar la ausencia de una correspondencia biunívoca en la región más amplia. Un autor ha sugerido una opción de donde ξ es la forma de la distribución generalizada de valores extremos , que es el límite de valores extremos de la distribución muestreada. ${\displaystyle [0,1]}$ ${\displaystyle f(p,N)}$ ${\displaystyle [1,N]}$ ${\displaystyle C={\tfrac {1}{2}}(1+\xi )}$

Primera variante,do= 1/2

El resultado de utilizar cada una de las tres variantes de la lista ordenada {15, 20, 35, 40, 50}

(Fuentes: Función "prctile" de Matlab, ^{[9] [10]} )

${\displaystyle x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{N},1\right].\end{cases}}}$

dónde

${\displaystyle p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N} }$

${\displaystyle \therefore p_{1}={\frac {1}{2N}},p_{N}={\frac {2N-1}{2N}}.}$

Además, dejemos que

${\displaystyle P_{i}=100p_{i}.}$

La relación inversa está restringida a una región más estrecha:

${\displaystyle p={\frac {1}{N}}\left(x-{\frac {1}{2}}\right),x\in (1,N)\cap \mathbb {R} .}$

Segunda variante,do= 1

[Fuente: Algunos paquetes de software, incluidos NumPy ^[11] y Microsoft Excel ^[3] (hasta la versión 2013 inclusive mediante la función PERCENTILE.INC). Señalado como una alternativa por el NIST . ^[8] ]

${\displaystyle x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]}$

${\displaystyle \therefore p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].}$

Tenga en cuenta que la relación es uno a uno para , la única de las tres variantes con esta propiedad; de ahí el sufijo "INC", para inclusivo , en la función de Excel. ${\displaystyle x\leftrightarrow p}$ ${\displaystyle p\in [0,1]}$

Tercera variante,do= 0

(La variante principal recomendada por NIST . ^[8] Adoptada por Microsoft Excel desde 2010 mediante la función PERCENTIL.EXC. Sin embargo, como indica el sufijo "EXC", la versión de Excel excluye ambos puntos finales del rango de p , es decir, , mientras que la versión "INC", la segunda variante, no lo hace; de ​​hecho, cualquier número menor que también se excluye y causaría un error). ${\displaystyle p\in (0,1)}$ ${\displaystyle {\frac {1}{N+1}}}$

${\displaystyle x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\\p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.}$

La inversa está restringida a una región más estrecha:

${\displaystyle p={\frac {x}{N+1}}{\text{, }}x\in (0,N).}$

El método del percentil ponderado

Además de la función de percentil, también existe un percentil ponderado , en el que se cuenta el porcentaje del peso total en lugar del número total. No existe una función estándar para un percentil ponderado. Un método extiende el enfoque anterior de manera natural.

Supongamos que tenemos pesos positivos asociados, respectivamente, con nuestros N valores de muestra ordenados. Sea ${\displaystyle w_{1},w_{2},w_{3},\dots ,w_{N}}$

${\displaystyle S_{N}=\sum _{k=1}^{N}w_{k},}$

la suma de los pesos. Luego, las fórmulas anteriores se generalizan tomando

${\displaystyle p_{n}={\frac {1}{S_{N}}}\left(S_{n}-{\frac {w_{n}}{2}}\right)}$cuando , ${\displaystyle C=1/2}$

o

${\displaystyle p_{n}={\frac {S_{n}-Cw_{n}}{S_{N}+(1-2C)w_{n}}}}$Para general , ${\displaystyle C}$

y

${\displaystyle v=v_{k}+{\frac {P-p_{k}}{p_{k+1}-p_{k}}}(v_{k+1}-v_{k}).}$

El percentil ponderado del 50% se conoce como mediana ponderada .

Véase también

• Portal de matemáticas

• Décimo
• Rango percentil
• Cuantil
• Resumen de estadísticas

Referencias

1. Hyndman, Rob J. ; Fan, Yanan (noviembre de 1996). "Sample Quantiles in Statistical Packages". American Statistician . 50 (4). Asociación Estadounidense de Estadística: 361–365. doi :10.2307/2684934. JSTOR  2684934.
2. Lane, David. "Percentiles" . Consultado el 15 de septiembre de 2007 .
3. Pottel, Hans. "Defectos estadísticos en Excel" (PDF) . Archivado desde el original (PDF) el 4 de junio de 2013. Consultado el 25 de marzo de 2013 .
4. Schoonjans F, De Bacquer D, Schmid P (2011). "Estimación de percentiles poblacionales". Epidemiología . 22 (5): 750–751. doi :10.1097/EDE.0b013e318225c1de. PMC 3171208 . PMID  21811118. 
5. Johnson, Robert; Kuby, Patricia (2007), "Ejemplo aplicado 2.15, El límite de velocidad del percentil 85: seguir el 85 % de la corriente", Estadística elemental (10.ª ed.), Cengage Learning, pág. 102, ISBN 9781111802493.
6. "Límites de velocidad racionales y la velocidad del percentil 85" (PDF) . lsp.org . Policía Estatal de Luisiana. Archivado desde el original (PDF) el 23 de septiembre de 2018 . Consultado el 28 de octubre de 2018 .
7. Wessa, P (2021). "Percentiles en software estadístico gratuito". Oficina de Investigación, Desarrollo y Educación . Consultado el 13 de noviembre de 2021 .
8. "Manual de estadística de ingeniería: percentil". NIST . Consultado el 18 de febrero de 2009 .
9. "Matlab Statistics Toolbox – Percentiles" . Consultado el 15 de septiembre de 2006 ., Esto es equivalente al método 5 que se analiza aquí.
10. Langford, E. (2006). "Cuartiles en estadística elemental". Revista de Educación en Estadística . 14 (3). doi : 10.1080/10691898.2006.11910589 .
11. "Documentación de NumPy 1.12". SciPy . Consultado el 19 de marzo de 2017 .