Esta lista parcial de grafos contiene definiciones de grafos y familias de grafos. Para obtener definiciones recopiladas de términos de teoría de grafos que no se refieren a tipos de grafos individuales, como vértice y camino , consulte Glosario de teoría de grafos . Para obtener enlaces a artículos existentes sobre tipos particulares de grafos, consulte Categoría:Gráficos . Algunas de las estructuras finitas consideradas en la teoría de grafos tienen nombres, a veces inspirados en la topología del grafo y a veces en honor a su descubridor. Un ejemplo famoso es el grafo de Petersen , un grafo concreto en 10 vértices que aparece como un ejemplo mínimo o contraejemplo en muchos contextos diferentes.
El gráfico fuertemente regular con vértices v y rango k se denota habitualmente como srg( v,k ,λ,μ).
Un grafo simétrico es aquel en el que existe una simetría ( automorfismo de grafo ) que lleva a cualquier par ordenado de vértices adyacentes a cualquier otro par ordenado; el censo de Foster enumera todos los grafos 3-regulares simétricos pequeños. Todo grafo fuertemente regular es simétrico, pero no al revés.
El gráfico completo sobre vértices a menudo se denomina -clique y normalmente se denota , del alemán komplett . [1]
El gráfico bipartito completo se suele denotar como . Para consultar la sección sobre gráficos en estrella, el gráfico equivale al ciclo de 4 (el cuadrado) que se presenta a continuación.
El gráfico de ciclos sobre vértices se denomina n-ciclo y suele denotarse como . También se le llama gráfico cíclico , polígono o n-gono . Casos especiales son el triángulo , el cuadrado y luego varios con nombres griegos: pentágono , hexágono , etc.
El gráfico de amistad F n se puede construir uniendo n copias del gráfico de ciclo C 3 con un vértice común. [2]

En teoría de grafos, el término fulereno se refiere a cualquier grafo plano regular de 3 caras con todas las caras de tamaño 5 o 6 (incluida la cara externa). De la fórmula del poliedro de Euler , V – E + F = 2 (donde V , E , F indican el número de vértices, aristas y caras), se deduce que hay exactamente 12 pentágonos en un fulereno y h = V /2 – 10 hexágonos. Por lo tanto, V = 20 + 2 h ; E = 30 + 3 h . Los grafos de fulereno son las representaciones de Schlegel de los compuestos de fulereno correspondientes.
G. Brinkmann y A. Dress desarrollaron un algoritmo para generar todos los fulerenos no isomorfos con un número determinado de caras hexagonales. [3] G. Brinkmann también proporcionó una implementación disponible gratuitamente, denominada fullgen.
El grafo completo sobre cuatro vértices forma el esqueleto del tetraedro y, de manera más general, los grafos completos forman esqueletos de símplices . Los grafos de hipercubos también son esqueletos de politopos regulares de dimensiones superiores .
Un snark es un gráfico cúbico sin puente que requiere cuatro colores en cualquier coloración de arista adecuada . El snark más pequeño es el gráfico de Petersen , que ya se mencionó anteriormente.
Una estrella S k es el grafo bipartito completo K 1, k . La estrella S 3 se llama grafo de garra.
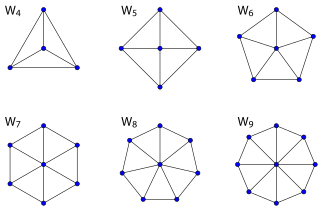
El gráfico de rueda W n es un gráfico en n vértices construido conectando un solo vértice a cada vértice en un ciclo ( n − 1).
Esta lista parcial contiene definiciones de gráficos y familias de gráficos que se conocen por nombres particulares, pero que no tienen un artículo de Wikipedia propio.

Un grafo de engranaje , denotado G n , es un grafo obtenido al insertar un vértice adicional entre cada par de vértices adyacentes en el perímetro de un grafo de rueda W n . Por lo tanto, G n tiene 2 n +1 vértices y 3 n aristas. [4] Los grafos de engranaje son ejemplos de grafos cuadrados y juegan un papel clave en la caracterización de grafos prohibidos de los grafos cuadrados. [5] Los grafos de engranaje también se conocen como ruedas dentadas y ruedas bipartitas .
Un gráfico de timón , denotado H n , es un gráfico que se obtiene uniendo un solo borde y nodo a cada nodo del circuito exterior de un gráfico de rueda W n . [6] [7]
Un gráfico de langosta es un árbol en el que todos los vértices están dentro de la distancia 2 de un camino central . [8] [9] Compárese con oruga .

El grafo de red W n , r es un grafo que consta de r copias concéntricas del grafo de ciclo C n , con vértices correspondientes conectados por "radios". Por lo tanto, W n ,1 es el mismo grafo que C n , y W n,2 es un prisma .
Un gráfico de red también se ha definido como un gráfico de prisma Y n +1, 3 , con los bordes del ciclo exterior eliminados. [7] [10]
{{cite web}}: CS1 maint: copia archivada como título ( enlace ){{cite web}}: Verificar |url=valor ( ayuda )