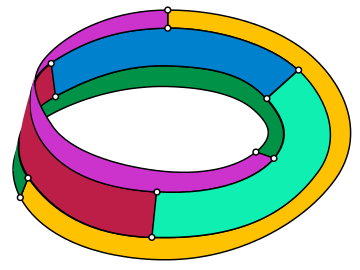
En el campo matemático de la teoría de grafos , el grafo de Tietze es un grafo cúbico no dirigido con 12 vértices y 18 aristas. Recibe su nombre en honor a Heinrich Franz Friedrich Tietze , quien demostró en 1910 que la banda de Möbius se puede subdividir en seis regiones que se tocan entre sí (tres a lo largo del límite de la banda y tres a lo largo de su línea central) y, por lo tanto, que los grafos que están incrustados en la banda de Möbius pueden requerir seis colores . [1] Los segmentos límite de las regiones de la subdivisión de Tietze (incluidos los segmentos a lo largo del límite de la propia banda de Möbius) forman una incrustación del grafo de Tietze.
El grafo de Tietze puede formarse a partir del grafo de Petersen reemplazando uno de sus vértices por un triángulo. [2] [3] Al igual que el grafo de Tietze, el grafo de Petersen forma el límite de seis regiones que se tocan mutuamente, pero en el plano proyectivo en lugar de en la banda de Möbius. Si se corta un agujero en esta subdivisión del plano proyectivo, rodeando un único vértice, el vértice rodeado se reemplaza por un triángulo de límites de regiones alrededor del agujero, lo que da la construcción descrita anteriormente del grafo de Tietze.
Tanto el gráfico de Tietze como el gráfico de Petersen son máximamente no hamiltonianos : no tienen ciclo hamiltoniano , pero dos vértices no adyacentes pueden estar conectados por un camino hamiltoniano . [2] El gráfico de Tietze y el gráfico de Petersen son los únicos gráficos cúbicos no hamiltonianos con 2 vértices conexos con 12 vértices o menos. [4]
A diferencia del gráfico de Petersen, el gráfico de Tietze no es hipohamiltoniano : al eliminar uno de sus tres vértices triangulares se forma un gráfico más pequeño que sigue siendo no hamiltoniano.
La coloración de los bordes del gráfico de Tietze requiere cuatro colores; es decir, su índice cromático es 4. De manera equivalente, los bordes del gráfico de Tietze se pueden dividir en cuatro coincidencias , pero no menos.
El gráfico de Tietze coincide en parte con la definición de un snark : es un gráfico cúbico sin puente que no es coloreable en sus 3 aristas. Sin embargo, la mayoría de los autores restringen los snarks a gráficos sin 3-ciclos, por lo que el gráfico de Tietze no se considera generalmente un snark. No obstante, es isomorfo al gráfico J 3 , parte de una familia infinita de snarks de flores introducidos por R. Isaacs en 1975. [5]
A diferencia del grafo de Petersen, el grafo de Tietze puede ser cubierto por cuatro emparejamientos perfectos . Esta propiedad desempeña un papel clave en una prueba de que comprobar si un grafo puede ser cubierto por cuatro emparejamientos perfectos es NP-completo . [6]
El grafo de Tietze tiene número cromático 3, índice cromático 4, circunferencia 3 y diámetro 3. El número de independencia es 5. Su grupo de automorfismos tiene orden 12 y es isomorfo al grupo diedro D 6 , el grupo de simetrías de un hexágono regular (incluyendo rotaciones y reflexiones). Este grupo tiene dos órbitas de tamaño 3 y una de tamaño 6 en los vértices, y por lo tanto este grafo no es transitivo en vértices .