Experimentos de Kaufmann-Bucherer-Neumann

Figura 1. Medición de Walter Kaufmann de la relación carga-masa del electrón para diferentes velocidades del electrón. Una fuente de radio en la parte inferior del aparato evacuado emitió partículas beta de energías variables. Los campos E y B paralelos en combinación con la apertura del orificio permitieron que sólo ciertas combinaciones de dirección y velocidad del electrón expusieran la placa fotográfica en la parte superior. (a) Esta vista frontal del aparato ilustra la aceleración uniforme impuesta por las placas condensadoras cargadas sobre las partículas beta. (b) Esta vista lateral del aparato ilustra el movimiento circular de las partículas beta transversales al campo B. (c) La placa fotográfica registró una raya curva que se analizó para determinar e/m para la variación de v siguiendo diferentes suposiciones teóricas.

Los experimentos de Kaufmann-Bucherer-Neumann midieron la dependencia de la masa inercial (o momento ) de un objeto con respecto a su velocidad . La importancia histórica de esta serie de experimentos realizados por varios físicos entre 1901 y 1915 se debe a que los resultados se utilizaron para probar las predicciones de la relatividad especial . La precisión y el análisis de datos de estos experimentos, así como la influencia resultante en la física teórica durante esos años, siguen siendo un tema de activa discusión histórica, ya que los primeros resultados experimentales contradecían en un principio la teoría de Einstein , entonces recién publicada (1905), ^[1] pero versiones posteriores de este experimento la confirmaron. Para experimentos modernos de ese tipo, véase Pruebas de energía y momento relativistas ; para información general, véase Pruebas de relatividad especial .

Contexto histórico

En 1896, Henri Becquerel descubrió la desintegración radiactiva en diversos elementos químicos . Posteriormente, se descubrió que la radiación beta de estas desintegraciones era la emisión de una partícula con carga negativa . Más tarde, estas partículas se identificaron con el electrón , descubierto en experimentos de rayos catódicos por JJ Thomson en 1897.

Esto estaba relacionado con la predicción teórica de la masa electromagnética por JJ Thomson en 1881, quien demostró que la energía electromagnética contribuye a la masa de un cuerpo cargado en movimiento . ^[2] Thomson (1893) y George Frederick Charles Searle (1897) también calcularon que esta masa depende de la velocidad, y que se vuelve infinitamente grande cuando el cuerpo se mueve a la velocidad de la luz con respecto al éter luminífero . ^[3] También Hendrik Antoon Lorentz (1899, 1900) asumió tal dependencia de la velocidad como consecuencia de su teoría de los electrones. ^[4] En este momento, la masa electromagnética se separó en masa "transversal" y "longitudinal", y a veces se denotaba como "masa aparente", mientras que la masa newtoniana invariante se denotaba como "masa real". ^{[A 1] [A 2]} Por otra parte, el teórico alemán Max Abraham creía que toda masa acabaría resultando ser de origen electromagnético y que la mecánica newtoniana quedaría subsumida en las leyes de la electrodinámica. ^{[A 3]}

En 1904, Lorentz propuso que la masa a lo largo de la trayectoria del movimiento (masa longitudinal) y la masa en las direcciones perpendiculares al movimiento (transversal) son diferentes. En su teoría, la masa longitudinal y la masa transversal , donde es el factor de Lorentz y es la masa en reposo del electrón. ^[5] El concepto de masa electromagnética (transversal) , que se basaba en modelos específicos del electrón, se transmutó más tarde en el concepto puramente cinemático de masa relativista que se refiere a todas las formas de energía, no solo a la energía electromagnética. Actualmente, sin embargo, el concepto de masa relativista, aunque todavía se hace referencia a él con frecuencia en obras populares sobre la relatividad, rara vez se utiliza entre los físicos profesionales y ha sido reemplazado por las expresiones para la energía y el momento relativistas , que también predicen que los cuerpos masivos no pueden alcanzar la velocidad de la luz. Esto se debe a que todas esas relaciones involucran el factor de Lorentz : ${\displaystyle m_{L}={{\gamma }^{3}}m}$ ${\displaystyle m_{T}={\gamma }m}$ ${\displaystyle \gamma }$ ${\displaystyle m}$ ${\displaystyle m_{T}}$

${\displaystyle {\frac {m_{T}}{m}}={\frac {p}{mv}}={\frac {E}{mc^{2}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

Por lo tanto, los experimentos de Bucherer-Kaufmann-Neumann pueden considerarse como pruebas tempranas de la energía y el momento relativistas . (Para la siguiente descripción histórica de los experimentos, todavía se utilizan los conceptos de "masa transversal" o "masa relativista").

Los experimentos de Kaufmann

Primeros experimentos

Figura 2. Las mediciones de Kaufmann de 1901 (corregidas en 1902) mostraron que la relación carga-masa disminuye y, por lo tanto, el momento (o masa) del electrón aumenta con la velocidad. Nótese que emu/gm cuando el electrón está en reposo. ${\displaystyle \scriptstyle \epsilon /m_{0}\sim 1.95\times 10^{7}}$

Walter Kaufmann comenzó a experimentar con rayos beta utilizando un dispositivo similar a un tubo de rayos catódicos , donde la fuente de los electrones era la desintegración del radio que se colocaba en un recipiente al vacío . (Véase la figura 1) Dichos rayos emitidos por el radio se denominaban en aquella época "rayos de Becquerel". A diferencia de los rayos catódicos conocidos entonces , que alcanzaban velocidades de sólo 0,3 c, siendo c la velocidad de la luz, los rayos de Becquerel alcanzaban velocidades de hasta 0,9 c . Sin embargo, como las partículas beta tienen velocidades diferentes, la radiación no era homogénea. Por tanto, Kaufmann aplicó campos eléctricos y magnéticos alineados en paralelo entre sí, de modo que las desviaciones causadas por ellos fueran perpendiculares entre sí. Sus impactos sobre una placa fotográfica producían una curva de deflexión, cuyos puntos individuales correspondían a una determinada velocidad y a una determinada masa de los electrones. Invirtiendo la carga en el condensador, invirtiendo así el campo eléctrico, se podrían obtener dos curvas simétricas, cuya línea central determina la dirección de la desviación magnética. ^{[A 4] [A 5]}

Kaufmann publicó un primer análisis de sus datos en 1901: de hecho, pudo medir una disminución de la relación carga-masa , demostrando así que la masa o el momento aumentan con la velocidad. ^[6] Utilizando la fórmula de Searle (1897) para el aumento de la energía electromagnética de los cuerpos cargados con la velocidad, calculó el aumento de la masa electromagnética del electrón en función de la velocidad:

${\displaystyle \phi (\beta )={\frac {3}{4\beta ^{2}}}\left[{\frac {1}{\beta }}\lg {\frac {1-\beta }{1+\beta }}+{\frac {2}{1-\beta ^{2}}}\right],\;\beta ={\frac {v}{c}}}$,

Kaufmann se dio cuenta de que el aumento observado no podía explicarse con esta fórmula, por lo que separó la masa total medida en una masa mecánica (verdadera) y una masa electromagnética (aparente) , siendo la masa mecánica considerablemente mayor que la electromagnética. Sin embargo, cometió dos errores: como demostró Max Abraham , Kaufmann pasó por alto que la fórmula de Searle solo se aplica en la dirección longitudinal, pero para las mediciones de deflexión era importante la fórmula para la dirección transversal. Por lo tanto, Abraham introdujo la "masa electromagnética transversal" con la siguiente dependencia de la velocidad:

${\displaystyle \phi (\beta )={\frac {3}{4\beta ^{2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1\right),}$

Kaufmann también cometió un error de cálculo al derivar las curvas de deflexión, errores que corrigió en 1902. ^[7]

En 1902 y 1903 Kaufmann realizó otra serie de pruebas con técnicas experimentales actualizadas y mejoradas. Los resultados fueron interpretados por él como una confirmación de la teoría de Abraham y de la suposición de que la masa del electrón es completamente de origen electromagnético. ^{[8] [9]}

Hermann Starke realizó mediciones similares en 1903, aunque utilizó rayos catódicos limitados a 0,3c. Los resultados que obtuvo fueron interpretados por él como acordes con los de Kaufmann. ^[10]

Teorías en competencia

Figura 3. Predicciones de la dependencia de la velocidad de la masa electromagnética transversal según las teorías de Abraham, Lorentz y Bucherer.

En 1902, Max Abraham publicó una teoría basada en el supuesto de que el electrón era una esfera rígida y perfecta , con su carga distribuida uniformemente sobre su superficie. Como se explicó anteriormente, introdujo la denominada "masa electromagnética transversal" además de la "masa electromagnética longitudinal", y argumentó que toda la masa del electrón es de origen electromagnético. ^{[A 6] [A 7] [11] [12] [13]}

Mientras tanto, Lorentz (1899, 1904) amplió su teoría de los electrones, suponiendo que la carga de un electrón se extendía por todo su volumen y que, en el experimento de Kaufmann, su forma se comprimiría en la dirección del movimiento y permanecería inalterada en las direcciones transversales. Para sorpresa de Kaufmann, Lorentz pudo demostrar que su modelo también concordaba con sus datos experimentales. Este modelo fue elaborado y perfeccionado por Henri Poincaré (1905), de modo que la teoría de Lorentz ahora estaba de acuerdo con el principio de relatividad . ^{[A 8] [A 9] [5] [14]}

En 1904, Alfred Bucherer y Paul Langevin desarrollaron una teoría similar , con la diferencia de que se suponía que el volumen total ocupado por el electrón deformado no cambiaba. Resultó que la predicción de esta teoría se acercaba más a la de Abraham que a la de Lorentz. ^{[A 10] [15]}

Finalmente, la teoría de la relatividad especial de Albert Einstein (1905) predijo el cambio de la masa del electrón puntual debido a las propiedades de la transformación entre el sistema de reposo de la partícula y el sistema de laboratorio en el que se realizaron las mediciones. Matemáticamente, este cálculo predice la misma dependencia entre velocidad y masa que la teoría de Lorentz, aunque asume conceptos físicos muy diferentes. ^{[A 11] [1]}

En cuanto al aumento de la masa electromagnética transversal , las predicciones de las distintas teorías fueron (Fig. 3):

${\displaystyle {\begin{aligned}&{\text{Abraham}}&\phi (\beta )&={\frac {3}{4\beta ^{2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1\right)\\&{\text{Lorentz--Einstein}}&\phi (\beta )&=(1-\beta ^{2})^{-1/2}\\&{\text{Bucherer--Langevin}}&\phi (\beta )&=(1-\beta ^{2})^{-1/3}\end{aligned}}}$

Experimentos de 1905

Para decidir entre estas teorías, Kaufmann volvió a realizar sus experimentos con mayor precisión. Kaufmann creía que había refutado de manera concluyente la fórmula de Lorentz-Einstein y, por lo tanto, también había refutado el principio de relatividad . En su opinión, las únicas opciones restantes eran entre las teorías de Abraham y Bucherer. Lorentz estaba perplejo y escribió que estaba " al final de su latín ". ^{[A 12] [A 13] [16] [17]}

Sin embargo, el experimento de Kaufmann fue criticado. ^{[A 14] [A 15]} Poco después de que Kaufmann publicara sus resultados y las conclusiones de su análisis, Max Planck decidió volver a analizar los datos obtenidos por el experimento. En 1906 y 1907, Planck publicó su propia conclusión sobre el comportamiento de la masa inercial de los electrones a altas velocidades. Utilizando sólo nueve puntos de datos de la publicación de Kaufmann en 1905, recalculó la configuración exacta de los campos para cada punto y comparó las mediciones con las predicciones de las dos teorías en competencia. Demostró que los resultados de Kaufmann no son totalmente decisivos y conducirían a velocidades superlumínicas. ^{[18] [19]} Einstein comentó en 1907 que, aunque los resultados de Kaufmann concordaban mejor con las teorías de Abraham y Bucherer que con las suyas, los fundamentos de las otras teorías no eran plausibles y, por lo tanto, tenían pocas probabilidades de ser correctos. ^[20]

Experimentos posteriores

Bucherer

El principal problema de los experimentos de Kaufmann fue el uso de campos magnéticos y eléctricos paralelos , como señaló Adolf Bestelmeyer (1907). Utilizando un método basado en campos magnéticos y eléctricos perpendiculares (introducido por JJ Thomson y desarrollado posteriormente hasta un filtro de velocidad por Wilhelm Wien ), Bestelmeyer obtuvo valores considerablemente diferentes para la relación carga-masa para rayos catódicos de hasta 0,3c. Sin embargo, Bestelmeyer añadió que su experimento no era lo suficientemente preciso como para proporcionar una decisión definitiva entre las teorías. ^[21]

Por ello, Alfred Bucherer (1908) realizó una medición precisa utilizando un filtro de velocidad similar al de Bestelmeyer. Véanse las figuras 4 y 5. Se colocó una fuente de radio beta en el centro de un condensador circular que constaba de dos placas de vidrio plateado separadas 0,25 mm y cargadas a unos 500 voltios, colocadas en un campo magnético homogéneo de 140 Gauss. El radio emitía rayos beta en todas las direcciones, pero en cualquier dirección particular α, solo salían del filtro de velocidad aquellos rayos beta cuya velocidad era tal que los campos eléctrico y magnético se compensaban exactamente entre sí. Después de salir del condensador, los rayos eran desviados por el campo magnético y exponían una placa fotográfica colocada paralela al borde del condensador y perpendicular a los rayos no desviados. ^{[22] [23]}

Para su análisis final, Bucherer recalculó los valores medidos de cinco ejecuciones con las fórmulas de Lorentz y Abraham respectivamente, con el fin de obtener la relación carga-masa como si los electrones estuvieran en reposo. Dado que la relación no varía para los electrones en reposo, los puntos de datos deberían estar en una sola línea horizontal (véase la figura 6). Sin embargo, esto fue aproximadamente solo en el caso en que los datos se calcularon con la fórmula de Lorentz, mientras que los resultados de la fórmula de Abraham se desviaron bruscamente (las líneas roja y azul representan el valor promedio según ambas fórmulas). La concordancia con la fórmula de Lorentz-Einstein fue interpretada por Bucherer como la confirmación del principio de relatividad y la teoría de Lorentz-Einstein, un resultado aplaudido inmediatamente por Lorentz, Einstein y Hermann Minkowski . ^{[A 16] [A 17]}

Además, el aparato de Bucherer fue mejorado en 1909 por su alumno Kurt Wolz, quien también obtuvo un acuerdo con la fórmula de Lorentz-Einstein (aunque no comparó la fórmula de Abraham con sus datos, Fig. 7). ^[24]

Aunque muchos físicos aceptaron el resultado de Bucherer, todavía quedaban algunas dudas. ^{[A 18] [A 19]} Por ejemplo, Bestelmeyer publicó un artículo en el que ponía en duda la validez del resultado de Bucherer. Argumentaba que un solo experimento no puede establecer la exactitud de una ley física importante, que el resultado de Bucherer podría estar significativamente distorsionado por rayos no compensados ​​que llegan a la placa fotográfica y que son necesarios amplios protocolos de datos y análisis de errores. ^[25] Una disputa polémica entre estos dos académicos siguió en una serie de publicaciones, en las que Bestelmeyer argumentó que los experimentos de Wolz se ven afectados por los mismos problemas. ^{[26] [27] [28]}

Hupka

A diferencia de Kaufmann y Bucherer, Karl Erich Hupka (1909) utilizó rayos catódicos a 0,5 °C para sus mediciones. La radiación (generada en un cátodo de cobre) fue acelerada fuertemente por el campo entre el cátodo y el ánodo en un tubo de descarga altamente evacuado. El ánodo que sirve de diafragma fue pasado por el rayo con velocidad constante y dibujó la imagen de sombra de dos alambres de Wollaston en una pantalla fosforescente detrás de un segundo diafragma. Si se generaba una corriente detrás de este diafragma, entonces el rayo se desviaba y la imagen de sombra se desplazaba. Los resultados concordaban con Lorentz-Einstein, aunque Hupka señaló que este experimento no representaba un resultado definitivo. ^[29] Posteriormente, W. Heil publicó algunos artículos que trataban con críticas e interpretaciones del resultado, a lo que Hupka respondió. ^{[30] [31] [32]}

Neumann y Guye/Lavanchy

Figura 8. Evaluación de Neumann de 26 puntos de datos para cada teoría.

En 1914, Günther Neumann realizó nuevas mediciones utilizando el equipo de Bucherer, en particular haciendo algunas mejoras para abordar las críticas de Bestelmeyer, especialmente la cuestión de los rayos no compensados, y haciendo amplios refinamientos a los protocolos de datos. El método de cálculo fue el mismo que el de Bucherer (ver Figura 6). También en este experimento, los datos correspondientes a la fórmula de Lorentz están casi en una línea horizontal como se requiere, mientras que los datos obtenidos a partir de la fórmula de Abraham se desvían bruscamente (ver Figura 8). Neumann concluyó que sus experimentos estaban de acuerdo con los de Bucherer y Hupka, demostrando definitivamente la fórmula de Lorentz-Einstein en el rango 0,4-0,7c, y refutó la fórmula de Abraham. Las incertidumbres instrumentales ocurrieron en el rango 0,7-0,8c, por lo que la desviación de la fórmula de Lorentz-Einstein en este rango no se consideró significativa. ^[33]

Figura 9. Evaluación de Guye y Lavanchy de 25 puntos de datos para cada teoría.

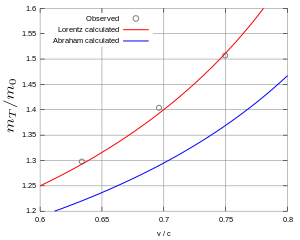
En 1915, Charles-Eugène Guye y Charles Lavanchy midieron la desviación de los rayos catódicos a 0,25c–0,5c. Utilizaron un tubo con un cátodo y un ánodo para acelerar los rayos. Un diafragma en el ánodo producía un haz que se desviaba. Se colocó una pantalla en el extremo del aparato, en el que se fotografiaron los impactos con una cámara. Posteriormente calcularon la relación entre la masa electromagnética transversal m _T y la masa en reposo m ₀ indicada por la curva roja y azul, y obtuvieron una buena concordancia con la fórmula de Lorentz-Einstein (véase la figura 9), complementando el resultado de Neumann. ^{[34] [35]}

Muchos consideraron que los experimentos de Neumann y Guye/Lavanchy demostraban de manera concluyente la fórmula de Lorentz-Einstein. ^{[A 20] [A 21] [A 22]} Lorentz resumió estos esfuerzos en 1915: ^{[A 23]}

Experimentos posteriores [...] han confirmado la fórmula [...] de la masa electromagnética transversal, de modo que, con toda probabilidad, la única objeción que podía plantearse contra la hipótesis del electrón deformable y el principio de relatividad ha sido eliminada.

Desarrollo adicional

Figura 10. Espectrógrafo electrostático de Rogers et al.

Zahn y Spees (1938) ^[36] y Faragó y Lajos Jánossy (1954) ^[37] argumentaron que muchas de las suposiciones empleadas en esos primeros experimentos en cuanto a la naturaleza y las propiedades de los electrones y la configuración experimental eran erróneas o imprecisas. Al igual que con los experimentos de Kaufmann, los experimentos de Bucherer-Neumann solo mostrarían un aumento cualitativo de la masa y no fueron capaces de decidir entre las teorías en competencia. ^{[A 24] [A 25]}

Aunque los resultados de esos experimentos de desviación de electrones fueron discutidos durante mucho tiempo, las investigaciones de la estructura fina de las líneas de hidrógeno realizadas por Karl Glitscher (basadas en el trabajo de Arnold Sommerfeld ) ya habían proporcionado en 1917 una clara confirmación de la fórmula de Lorentz-Einstein, porque las expresiones relativistas para el momento y la energía eran necesarias para derivar la estructura fina, y constituían una refutación de la teoría de Abraham. ^{[38] [A 26]}

Figura 11. Tres puntos de datos de Rogers et al ., de acuerdo con la fórmula de Lorentz-Einstein.

Además, los primeros experimentos de deflexión de electrones con suficiente precisión fueron realizados por Rogers et al. (1940), quienes desarrollaron una configuración mejorada. La serie de desintegración del radio produce un espectro de partículas beta con una amplia gama de energías. Las mediciones anteriores de Kaufmann, Bucherer y otros habían utilizado condensadores de placas paralelas planas que no proporcionaban enfoque de las partículas beta. Rogers et al. (Fig. 10) en su lugar construyeron un espectrógrafo electrostático capaz de resolver los máximos de energía de las líneas de partículas beta individuales de la serie de desintegración del radio. El espectrógrafo electrostático se construyó con segmentos de dos cilindros y estaba encerrado en una caja de hierro evacuada. Los rayos beta se emitían desde un fino alambre de platino recubierto con depósito activo de radio. Los rayos dispersos incidían en una rendija frente a un contador Geiger . Los datos de este experimento se combinaron con mediciones previas de H _ρ realizadas con espectrómetros magnéticos para obtener la relación carga-masa, que posteriormente se comparó con las predicciones de Lorentz y Abraham para la relación entre la masa transversal y la masa en reposo. Todos los puntos estaban en la curva que representa la fórmula de Lorentz-Einstein con una precisión del 1 % (véase la figura 11). ^[39] Se considera que este experimento es lo suficientemente preciso como para distinguir entre las teorías. ^{[A 27]}

Pruebas modernas

Desde entonces, se han llevado a cabo muchos otros experimentos relacionados con la relación energía-momento relativista , incluidas mediciones de la desviación de los electrones, todos ellos confirmando la relatividad especial con gran precisión. También en los aceleradores de partículas modernos , las predicciones de la relatividad especial se confirman de forma rutinaria.

Véase también

• Historia de la relatividad especial

Referencias

Fuentes primarias

1. Einstein, Albert (1905), "Zur Elektrodynamik bewegter Körper" (PDF) , Annalen der Physik , 322 (10): 891–921, Bibcode :1905AnP...322..891E, doi : 10.1002/andp.19053221004 , hdl :10915/2786. Véase también: Traducción al inglés.
2. Thomson, JJ (1881), "Sobre los efectos eléctricos y magnéticos producidos por el movimiento de cuerpos electrificados" (PDF) , Philosophical Magazine , 5, 11 (68): 229–249, doi :10.1080/14786448108627008
3. Searle, GFC (1897), "Sobre el movimiento constante de un elipsoide electrificado" (PDF) , Philosophical Magazine , 5, 44 (269): 329–341, doi :10.1080/14786449708621072
4. Lorentz, HA (1900), "Über die scheinbare Masse der Ionen (Sobre la masa aparente de los iones)", Physikalische Zeitschrift , 2 (5): 78–80
5. Lorentz, Hendrik Antoon (1904), "Fenómenos electromagnéticos en un sistema que se mueve con una velocidad menor que la de la luz"  , Actas de la Real Academia de Artes y Ciencias de los Países Bajos , 6 : 809–831, Bibcode :1903KNAB....6..809L
6. Kaufmann, W. (1901), "Die magnetische und elektrische Ablenkbarkeit der Bequerelstrahlen und die scheinbare Masse der Elektronen", Göttinger Nachrichten (2): 143–168
7. Kaufmann, W. (1902), "Über die elektromagnetische Masse des Elektrons", Göttinger Nachrichten (5): 291–296
8. Kaufmann, W. (1902), "Die elektromagnetische Masse des Elektrons (La masa electromagnética del electrón)"  , Physikalische Zeitschrift , 4 (1b): 54–56
9. Kaufmann, W. (1903), "Über die "Elektromagnetische Masse" der Elektronen", Göttinger Nachrichten (3): 90-103
10. Starke, H. (1903). "Über die elektrische und magnetische Ablenkung schneller Kathodenstrahlen". Verhandlungen der Deutschen Physikalischen Gesellschaft (13): 241–250.
11. Abraham, M. (1902). "Dinámica de los electrones"  . Göttinger Nachrichten : 20–41.
12. Abraham, M. (1902). "Prinzipien der Dynamik des Elektrons (Principios de la dinámica del electrón (1902))"  . Physikalische Zeitschrift . 4 (1b): 57–62.
13. Abraham, M. (1903). "Prinzipien der Dynamik des Elektrons" (PDF) . Annalen der Physik . 10 (1): 105-179. Código Bib : 1902AnP...315..105A. doi : 10.1002/andp.19023150105.
14. Poincaré, Henri (1906), "Sur la dynamique de l'électron (Sobre la dinámica del electrón)", Rendiconti del Circolo Matematico di Palermo , 21 : 129–176, Bibcode : 1906RCMP...21..129P, doi : 10.1007/BF03013466, hdl : 2027/uiug.30112063899089 , S2CID  120211823
15. AH Bucherer, Mathematische Einführung in die Elektronentheorie, Teubner, Leipzig 1904, p. 57
16. Kaufmann, W. (1905), "Über die Konstitution des Elektrons (Sobre la constitución del electrón)"  , Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (45): 949–956
17. Kaufmann, W. (1906), "Über die Konstitution des Elektrons (Sobre la constitución del electrón)" (PDF) , Annalen der Physik , 19 (3): 487–553, Bibcode :1906AnP...324.. 487K, doi :10.1002/andp.19063240303
18. Planck, Max (1906), "Die Kaufmannschen Messungen der Ablenkbarkeit der β-Strahlen in ihrer Bedeutung für die Dynamik der Elektronen (Las medidas de Kaufmann sobre la desviabilidad de los rayos β en su importancia para la dinámica de los electrones)"  , Physikalische Zeitschrift , 7 : 753–761
19. Planck M (1907). "Nachtrag zu der Besprechung der Kaufmannschen Ablenkungsmessungen". Verhandlungen der Deutschen Physikalischen Gesellschaft . 9 .
20. Einstein, Albert (1908), "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen", Jahrbuch der Radioaktivität und Elektronik , 4 : 411–462, Bibcode : 1908JRE..... 4.. 411E
21. Bestelmeyer, A. (1907). "Spezifische Ladung und Geschwindigkeit der durch Röntgenstrahlen erzeugten Kathodenstrahlen". Annalen der Physik . 327 (3): 429–447. Código bibliográfico : 1907AnP...327..429B. doi : 10.1002/andp.19073270303.
22. Bucherer, AH (1908), "Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie. (Medidas de los rayos Becquerel. La confirmación experimental de la teoría de Lorentz-Einstein)", Physikalische Zeitschrift , 9 (22): 755– 762
23. Bucherer, AH (1909). "Die experimentelle Bestätigung des Relativitätsprinzips". Annalen der Physik . 333 (3): 513–536. Código bibliográfico : 1909AnP...333..513B. doi : 10.1002/andp.19093330305.
24. Wolz, Kurt (1909). "Die Bestimmung von e/m0". Annalen der Physik . 335 (12): 273–288. Código bibliográfico : 1909AnP...335..273W. doi : 10.1002/andp.19093351206.
25. Bestelmeyer, AH (1909). "Bemerkungen zu der Abhandlung Hrn. AH Bucherers: Die experimentelle Bestätigung des Relativitätsprinzips". Annalen der Physik . 335 (11): 166-174. Código bibliográfico : 1909AnP...335..166B. doi : 10.1002/andp.19093351105.
26. Bucherer, AH (1909). "Antwort auf die Kritik des Hrn. E. Bestelmeyer bezüglich meiner experimentellen Bestätigung des Relativitätsprinzips". Annalen der Physik . 335 (11): 974–986. Código bibliográfico : 1909AnP...335..974B. doi : 10.1002/andp.19093351506.
27. Bestelmeyer, AH (1910). "Erwiderung auf die Antwort des Hrn. AH Bucherer". Annalen der Physik . 337 (6): 231–235. Código bibliográfico : 1910AnP...337..231B. doi : 10.1002/andp.19103370609.
28. Bucherer, AH (1910). "Erwiderung auf die Bemerkungen des Hrn. A. Bestelmeyer". Annalen der Physik . 338 (14): 853–856. Código bibliográfico : 1910AnP...338..853B. doi : 10.1002/andp.19103381414.
29. Hupka, E. (1910). "Beitrag zur Kenntnis der trägen Masse bewegter Elektronen". Annalen der Physik . 336 (1): 169–204. Código Bib : 1909AnP...336..169H. doi : 10.1002/andp.19093360109.
30. Heil, W. (1910). "Diskussion der Versuche über die träge Masse bewegter Elektronen". Annalen der Physik . 336 (3): 519–546. Código bibliográfico : 1910AnP...336..519H. doi : 10.1002/andp.19103360305.
31. Hupka, E. (1910). "Zur Frage der trägen Masse bewegter Elektronen". Annalen der Physik . 338 (12): 400–402. Código bibliográfico : 1910AnP...336..519H. doi : 10.1002/andp.19103360305.
32. Heil, W. (1910). "Zur Diskussion der Hupkaschen Versuche über die träge Masse bewegter Elektronen". Annalen der Physik . 338 (12): 403–413. Código bibliográfico : 1910AnP...338..403H. doi : 10.1002/andp.19103381210.
33. Neumann, Günther (1914). "Die träge Masse schnell bewegter Elektronen". Annalen der Physik . 350 (20): 529–579. Código Bib : 1914AnP...350..529N. doi : 10.1002/andp.19143502005. hdl : 2027/uc1.b2608188 .
34. CE Guye; C. Lavanchy (1915). "Verificación experimental de la fórmula de Lorentz-Einstein par les rayons cathodiques de grande vitesse". CR Acad. Ciencia . 161 : 52–55.
35. CE Guye; C. Lavanchy (1915). "Verificación experimental de la fórmula de Lorentz-Einstein par les rayons cathodiques de grande vitesse". Archivos de ciencias físicas y naturales . 42 : 286 y siguientes.
36. Zahn, CT; Spees, AA (1938), "Un análisis crítico de los experimentos clásicos sobre la variación de la masa del electrón", Physical Review , 53 (7): 511–521, Bibcode :1938PhRv...53..511Z, doi :10.1103/PhysRev.53.511
37. PS Faragó; L. Jánossy (1957), "Revisión de la evidencia experimental de la ley de variación de la masa del electrón con la velocidad", Il Nuovo Cimento , 5 (6): 379–383, Bibcode :1957NCim....5.1411F, doi :10.1007/BF02856033, S2CID  121179531
38. Glitscher, Karl (1917). "Spektroskopischer Vergleich zwischen den Theorien des starren und des deformierbaren Elektrons". Annalen der Physik . 357 (6): 608–630. Código bibliográfico : 1917AnP...357..608G. doi : 10.1002/andp.19173570603. hdl :2027/uc1.b2637473.
39. Rogers, MM; et al. (1940), "Una determinación de las masas y velocidades de tres partículas beta de radio B", Physical Review , 57 (5): 379–383, Bibcode :1940PhRv...57..379R, doi :10.1103/PhysRev.57.379

Fuentes secundarias

• Battimelli, G. (1981). "La masa electromagnética del electrón: un estudio de caso de un experimento no crucial". Fundamenta Scientiae . 2 : 137–150.
• Janssen, Michel; Mecklenburg, Matthew (2007), "De la mecánica clásica a la relativista: modelos electromagnéticos del electrón", en VF Hendricks; et al. (eds.), Interactions: Mathematics, Physics and Philosophy , Dordrecht: Springer, págs. 65–134

• Lorentz, Hendrik Antoon (1916), La teoría de los electrones y sus aplicaciones a los fenómenos de la luz y el calor radiante, Leipzig y Berlín: BG Teubner

• Miller, Arthur I. (1981), La teoría especial de la relatividad de Albert Einstein. Surgimiento (1905) e interpretación temprana (1905-1911) , Lectura: Addison–Wesley, ISBN 0-201-04679-2

• Pais, Abraham (2005) [Publicado por primera vez en 1982], Sutil es el Señor: La ciencia y la vida de Albert Einstein , Nueva York: Oxford University Press, ISBN 0-19-280672-6

• Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften , vol. 5, págs. 539–776

  En inglés: Pauli, W. (1981) [1921]. "Teoría de la relatividad". Teorías fundamentales de la física . Vol. 165. Dover Publications. ISBN 0-486-64152-X.

• Staley, Richard (2008), La generación de Einstein , Chicago: University Press, ISBN 978-0-226-77057-4

1. Miller (1981), págs. 45-47
2. Pais (1982), págs. 155-159
3. Miller (1981), págs. 55-67
4. Miller (1981), págs. 47-54
5. Staley (2009), págs. 223-233
6. Miller (1981), págs. 55-67
7. Staley (2008), págs. 229-233
8. Miller (1981), págs. 55-67
9. Janssen (2007), sección 4
10. Janssen (2007), sección 4
11. Staley (2008), págs. 241-242
12. Miller (1981), págs. 228-232
13. Staley (2008), págs. 242-244
14. Miller (1981), págs. 232-235
15. Staley (2008), págs. 244-250
16. Miller (1981), págs. 345-350
17. Staley (2008), págs. 250-254
18. Miller (1981), págs. 345-350
19. Staley (2008), págs. 250-254
20. Pauli (1921), pág. 636
21. Miller (1981), págs. 350-351
22. Staley (2008), págs. 254-257
23. Lorentz (1915), pág. 339
24. Miller (1981), págs. 351-352
25. Janssen (2007), sección 7
26. Pauli (1921), págs. 636-637
27. Janssen (2007), sección 7

Enlaces externos

• Presentación del experimento de Kaufmann (PowerPoint)
• Lista de pruebas SR