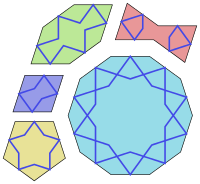
Los azulejos Girih son un conjunto de cinco azulejos que se utilizaron en la creación de patrones geométricos islámicos utilizando correas ( girih ) para la decoración de edificios en la arquitectura islámica . Se han utilizado desde aproximadamente el año 1200 y su disposición experimentó mejoras significativas a partir delsantuario Darb-i Imam en Isfahán , Irán , construido en 1453.
Las cinco formas de los azulejos y sus nombres persas son: [1]
Todos los lados de estas figuras tienen la misma longitud y todos sus ángulos son múltiplos de 36° (π/5 radianes ). Todos ellos, excepto el pentágono, tienen simetría bilateral (reflexión) a través de dos líneas perpendiculares. Algunos tienen simetrías adicionales. Específicamente, el decágono tiene simetría rotacional diez veces mayor (rotación de 36°); y el pentágono tiene simetría rotacional quíntuple (rotación de 72°).
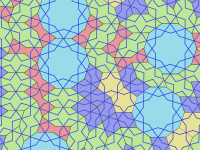
A finales del siglo XI, los artistas islámicos del norte de África comenzaron a utilizar el " mosaico de azulejos ", que es el predecesor de la teselación . [2] En el siglo XIII, los islámicos descubrieron una nueva forma de construir el “mosaico de azulejos” debido al desarrollo del cálculo aritmético y la geometría: los azulejos girih. [3]
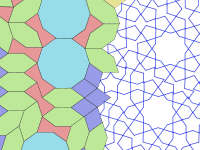
Girih son líneas ( cintas ) que decoran los azulejos. Los azulejos se utilizan para formar patrones girih, de la palabra persa گره , que significa "nudo". [4] En la mayoría de los casos, sólo el girih (y otras decoraciones menores como flores) son visibles en lugar de los límites de los mosaicos mismos. Los girih son líneas rectas divididas en trozos que cruzan los límites de las baldosas en el centro de un borde a 54° (3π/10 radianes) del borde. Dos girih que se cruzan cruzan cada borde de una baldosa. La mayoría de los mosaicos tienen un patrón único de girih dentro del mosaico que son continuos y siguen la simetría del mosaico. Sin embargo, el decágono tiene dos posibles patrones de girih, uno de los cuales tiene sólo una simetría rotacional quíntuple en lugar de diez veces mayor.
En 2007, los físicos Peter J. Lu y Paul J. Steinhardt sugirieron que los mosaicos girih poseen propiedades consistentes con los mosaicos fractales cuasicristalinos autosimilares, como los mosaicos de Penrose , que los precedieron cinco siglos. [5] [6]
Este hallazgo fue respaldado tanto por el análisis de patrones en las estructuras supervivientes como por el examen de pergaminos persas del siglo XV. No hay indicios de cuánto más sabían los arquitectos sobre las matemáticas involucradas. En general, se cree que tales diseños se construyeron trazando contornos en zigzag con sólo una regla y un compás. Es posible que se hayan consultado plantillas encontradas en pergaminos como el Rollo de Topkapi , de 97 pies (29,5 metros) de largo. Hallado en el Palacio de Topkapi en Estambul, el centro administrativo del Imperio Otomano, y que se cree que data de finales del siglo XV, el rollo muestra una sucesión de patrones geométricos bidimensionales y tridimensionales. No hay texto, pero hay un patrón de cuadrícula y un código de colores que se utiliza para resaltar simetrías y distinguir proyecciones tridimensionales. Dibujos como los que se muestran en este pergamino habrían servido como libros de patrones para los artesanos que fabricaban los azulejos, y las formas de los azulejos girih dictaban cómo se podían combinar en patrones grandes. De esta manera, los artesanos podían realizar diseños muy complejos sin recurrir a las matemáticas y sin necesariamente comprender sus principios subyacentes. [7]
Este uso de patrones repetidos creados a partir de un número limitado de formas geométricas disponibles para los artesanos de la época es similar a la práctica de los artesanos góticos europeos contemporáneos . Los diseñadores de ambos estilos se preocuparon por utilizar sus inventarios de formas geométricas para crear la máxima diversidad de formas. Esto exigía una habilidad y una práctica muy diferentes a las matemáticas. [7]
Primero, divide el ángulo recto A en cinco partes del mismo grado creando cuatro rayos que comienzan desde A. Encuentra un punto arbitrario C en el segundo rayo y deja caer perpendiculares desde C a los lados del ángulo A en el sentido contrario a las agujas del reloj. Este paso crea el rectángulo ABCD junto con cuatro segmentos, cada uno de los cuales tiene un punto final en A; otros puntos finales son las intersecciones de los cuatro rayos con los dos lados de BC y DC del rectángulo ABCD. Luego, encuentre el punto medio del cuarto segmento creado a partir del punto E del cuarto rayo. Construya un arco con centro A y radio AE para intersecar a AB en el punto F y el segundo rayo en el punto G. El segundo segmento ahora es parte del rectángulo. diagonal. Traza una línea paralela a AD y que pasa por el punto G que corta el primer rayo en el punto H y el tercer rayo en el punto I. La línea HF pasa por el punto E y corta el tercer rayo en L y la línea AD en J. Construye una línea pasando por J que es paralelo al tercer rayo. Construya también la línea EI y encuentre M, que es la intersección de esta línea con AD. Desde el punto F, trace una línea paralela al tercer rayo para encontrarse con el primer rayo en K. Construya los segmentos GK, GL y EM. Encuentre el punto N tal que GI = IN construyendo un círculo con centro I y radio IG. Construya la línea DN que es paralela a GK para intersectar la línea que emana de J, y encuentre P para completar el pentágono regular EINPJ. La línea DN corta la bisectriz perpendicular de AB en Q. Desde Q construya una línea paralela a FK para intersectar al rayo MI en R. Como se muestra en la figura, usando O, que es el centro del rectángulo ABCD como centro de rotación de 180° , se puede hacer la región fundamental para el mosaico. [1]




Primero, divide el ángulo recto en cinco ángulos congruentes. Se selecciona un punto arbitrario P en el primer rayo en sentido antihorario. Para el radio del círculo inscrito en el decagramo, se selecciona la mitad del segmento creado a partir del tercer rayo, el segmento AM. La siguiente figura ilustra una solución visual paso a paso con regla y compás al problema realizada por el autor. [1] Tenga en cuenta que la forma de dividir un ángulo recto en cinco ángulos congruentes no forma parte de las instrucciones proporcionadas, porque se considera un paso elemental para los diseñadores.

El girih se ha aplicado ampliamente en la arquitectura. Los girih de las ventanas geométricas persas cumplen con los requisitos de la arquitectura persa. Los tipos específicos de adornos utilizados en orosi típicamente vinculaban las ventanas con la eminencia social y política del patrón. Cuanto más ornamentada sea una ventana, mayor será el estatus social y económico que tendrá el propietario. Un buen ejemplo de esto es Azad Koliji, un jardín de Dowlatabad en Irán [ cita requerida ] . Los patrones girih en su ventana demuestran con éxito múltiples capas. La primera capa sería el jardín real, que la gente puede vislumbrar cuando abren la ventana. Luego está el primer patrón girih en el exterior de la ventana, el patrón tallado. Otra capa artificial está representada por el colorido cristal de la ventana, cuyas capas multicolores crean la sensación de una masa de flores. Esta capa abstracta forma una clara contradicción con la capa real fuera de la ventana y da espacio a la imaginación. [8]