Un locus de rasgo cuantitativo ( QTL ) es un locus (sección de ADN ) que se correlaciona con la variación de un rasgo cuantitativo en el fenotipo de una población de organismos . [1] Los QTL se mapean identificando qué marcadores moleculares (como SNP o AFLP ) se correlacionan con un rasgo observado. Este suele ser un primer paso para identificar los genes reales que causan la variación del rasgo.
Un locus de rasgo cuantitativo ( QTL ) es una región de ADN que está asociada con un rasgo fenotípico particular , que varía en grado y que puede atribuirse a efectos poligénicos , es decir, el producto de dos o más genes y su entorno. [2] Estos QTL se encuentran a menudo en diferentes cromosomas . El número de QTL que explican la variación en el rasgo fenotípico indica la arquitectura genética de un rasgo. Puede indicar que la altura de la planta está controlada por muchos genes de pequeño efecto, o por unos pocos genes de gran efecto. [ cita requerida ]
Por lo general, los QTL subyacen a rasgos continuos (aquellos rasgos que varían continuamente, por ejemplo, la altura) en oposición a rasgos discretos (rasgos que tienen dos o varios valores característicos, por ejemplo, el cabello rojo en los humanos, un rasgo recesivo, o los guisantes lisos frente a los arrugados utilizados por Mendel en sus experimentos).
Además, un rasgo fenotípico único suele estar determinado por muchos genes. En consecuencia, muchos QTL están asociados a un único rasgo. Otro uso de los QTL es identificar genes candidatos subyacentes a un rasgo. La secuencia de ADN de cualquier gen en esta región se puede comparar entonces con una base de datos de ADN de genes cuya función ya se conoce, tarea que resulta fundamental para la mejora de los cultivos asistida por marcadores. [3]
La herencia mendeliana fue redescubierta a principios del siglo XX. A medida que las ideas de Mendel se difundían, los genetistas comenzaron a conectar las reglas de Mendel sobre la herencia de factores individuales con la evolución darwiniana . Para los primeros genetistas, no estaba inmediatamente claro que la variación uniforme en rasgos como el tamaño corporal (es decir, la dominancia incompleta ) fuera causada por la herencia de factores genéticos individuales. Aunque el propio Darwin observó que las características endogámicas de las palomas de lujo se heredaban de acuerdo con las leyes de Mendel (aunque Darwin en realidad no conocía las ideas de Mendel cuando hizo la observación), no era obvio que estas características seleccionadas por los criadores de palomas de lujo pudieran explicar de manera similar la variación cuantitativa en la naturaleza. [4]
Un intento temprano de William Ernest Castle de unificar las leyes de la herencia mendeliana con la teoría de la especiación de Darwin invocó la idea de que las especies se vuelven distintas entre sí a medida que una especie u otra adquiere un nuevo factor mendeliano. [5] La conclusión de Castle se basó en la observación de que los rasgos nuevos que podrían estudiarse en el laboratorio y que muestran patrones de herencia mendeliana reflejan una gran desviación del tipo salvaje, y Castle creía que la adquisición de tales características es la base de la "variación discontinua" que caracteriza a la especiación. [5] Darwin discutió la herencia de características mutantes similares, pero no las invocó como un requisito de la especiación. [4] En cambio, Darwin utilizó la aparición de tales características en poblaciones reproductoras como evidencia de que la mutación puede ocurrir al azar dentro de las poblaciones reproductoras, que es una premisa central de su modelo de selección en la naturaleza. [4] Más tarde en su carrera, Castle refinaría su modelo de especiación para permitir que una pequeña variación contribuya a la especiación a lo largo del tiempo. También pudo demostrar este punto mediante la cría selectiva de poblaciones de ratas de laboratorio para obtener un fenotipo encapuchado a lo largo de varias generaciones. [6]
El de Castle fue quizás el primer intento realizado en la literatura científica para dirigir la evolución mediante la selección artificial de un rasgo con variación subyacente continua; sin embargo, la práctica ya había sido ampliamente empleada en el desarrollo de la agricultura para obtener ganado o plantas con características favorables a partir de poblaciones que muestran variación cuantitativa en rasgos como el tamaño corporal o el rendimiento de grano. [ cita requerida ]
El trabajo de Castle fue uno de los primeros en intentar unificar las leyes recientemente redescubiertas de la herencia mendeliana con la teoría de la evolución de Darwin. Aun así, pasarían casi treinta años hasta que el marco teórico para la evolución de los rasgos complejos se formalizara ampliamente. [7] En un resumen temprano de la teoría de la evolución de la variación continua, Sewall Wright , un estudiante de posgrado que se formó con Castle, resumió el pensamiento contemporáneo sobre la base genética de la variación natural cuantitativa: "A medida que continuaban los estudios genéticos, se descubrió que cada vez había diferencias más pequeñas que mendelizaban, y cualquier carácter, investigado lo suficiente, resultó estar afectado por muchos factores". [7] Wright y otros formalizaron la teoría de la genética de poblaciones que se había elaborado durante los 30 años anteriores, explicando cómo se pueden heredar dichos rasgos y crear poblaciones de reproducción estable con características únicas. La genética cuantitativa de rasgos hoy en día aprovecha las observaciones de Wright sobre la relación estadística entre el genotipo y el fenotipo en familias y poblaciones para comprender cómo ciertas características genéticas pueden afectar la variación en poblaciones naturales y derivadas. [ cita requerida ]
La herencia poligénica se refiere a la herencia de una característica fenotípica (rasgo) que es atribuible a dos o más genes y puede medirse cuantitativamente. La herencia multifactorial se refiere a la herencia poligénica que también incluye interacciones con el medio ambiente. A diferencia de los rasgos monogénicos , los rasgos poligénicos no siguen patrones de herencia mendeliana (categorías discretas). En cambio, sus fenotipos varían típicamente a lo largo de un gradiente continuo representado por una curva de campana . [8]
Un ejemplo de un rasgo poligénico es la variación del color de la piel humana . Varios genes influyen en la determinación del color natural de la piel de una persona, por lo que modificar solo uno de esos genes puede cambiar el color de la piel levemente o, en algunos casos, como en el caso de SLC24A5 , moderadamente. Muchos trastornos con componentes genéticos son poligénicos, incluidos el autismo , el cáncer , la diabetes y muchos otros. La mayoría de las características fenotípicas son el resultado de la interacción de múltiples genes. [ cita requerida ]
Se dice que las enfermedades hereditarias multifactoriales constituyen la mayoría de los trastornos genéticos que afectan a los seres humanos y que darán lugar a hospitalización o atención especial de algún tipo. [9] [10]
Los rasgos controlados tanto por el medio ambiente como por factores genéticos se denominan multifactoriales. Por lo general, los rasgos multifactoriales ajenos a la enfermedad dan lugar a lo que vemos como características continuas en los organismos, especialmente en los organismos humanos, como la altura, [9] el color de la piel y la masa corporal. [11] Todos estos fenotipos se complican por una gran cantidad de intercambios entre genes y efectos ambientales. [9] La distribución continua de rasgos como la altura y el color de la piel descrita anteriormente refleja la acción de genes que no manifiestan patrones típicos de dominancia y recesividad. En cambio, se cree que las contribuciones de cada locus involucrado son aditivas. Los autores han distinguido este tipo de herencia como poligénica o herencia cuantitativa . [12]
Por lo tanto, debido a la naturaleza de los rasgos poligénicos, la herencia no seguirá el mismo patrón que un simple cruce monohíbrido o dihíbrido . [10] La herencia poligénica puede explicarse como herencia mendeliana en muchos loci, [9] lo que da como resultado un rasgo que se distribuye normalmente . Si n es el número de loci involucrados, entonces los coeficientes de la expansión binomial de ( a + b ) 2n darán la frecuencia de distribución de todas las n combinaciones de alelos . Para valores suficientemente altos de n , esta distribución binomial comenzará a parecerse a una distribución normal. Desde este punto de vista, un estado de enfermedad se hará evidente en una de las colas de la distribución, más allá de un valor umbral. Se esperarán estados de enfermedad de gravedad creciente a medida que uno se aleja del umbral y se aleja de la media . [12]
Una mutación que da lugar a una enfermedad suele ser recesiva, por lo que ambos alelos deben ser mutantes para que la enfermedad se exprese fenotípicamente. Una enfermedad o síndrome también puede ser el resultado de la expresión de alelos mutantes en más de un locus. Cuando interviene más de un gen, con o sin la presencia de desencadenantes ambientales, decimos que la enfermedad es el resultado de una herencia multifactorial. [ cita requerida ]
Cuantos más genes estén implicados en el cruce, más se parecerá la distribución de los genotipos a una distribución normal o gaussiana . [9] Esto demuestra que la herencia multifactorial es poligénica y que las frecuencias genéticas se pueden predecir mediante un cruce mendeliano polihíbrido . Las frecuencias fenotípicas son un asunto diferente, especialmente si se ven complicadas por factores ambientales. [ cita requerida ]
El paradigma de la herencia poligénica utilizado para definir enfermedades multifactoriales ha suscitado muchos desacuerdos. Turnpenny (2004) analiza cómo la herencia poligénica simple no puede explicar algunas enfermedades como la aparición de diabetes mellitus tipo I y que en casos como estos no se cree que todos los genes hagan una contribución igual. [12]
La suposición de la herencia poligénica es que todos los loci involucrados contribuyen por igual a los síntomas de la enfermedad. Esto debería dar como resultado una distribución normal (gaussiana) de genotipos. Cuando no es así, no se puede sustentar la idea de la herencia poligénica para esa enfermedad. [ cita requerida ]
Los ejemplos anteriores son bien conocidos de enfermedades que tienen componentes tanto genéticos como ambientales. Otros ejemplos incluyen enfermedades atópicas como el eczema o la dermatitis , [9] la espina bífida (columna vertebral abierta) y la anencefalia (cráneo abierto). [13]
Aunque los biopsiquiatras creen ampliamente que la esquizofrenia es multifactorialmente genética , no se han determinado con certeza marcadores genéticos característicos. [ cita requerida ]
Si se demuestra que los hermanos y hermanas del paciente padecen la enfermedad, entonces hay una gran probabilidad de que la enfermedad sea genética [ cita requerida ] y de que el paciente también sea portador genético. Esto no es suficiente, ya que también es necesario demostrar que el patrón de herencia no es mendeliano. Esto requeriría estudiar docenas, incluso cientos de diferentes genealogías familiares antes de llegar a la conclusión de que se trata de una herencia multifactorial. Esto a menudo lleva varios años. [ cita requerida ]
Si la herencia multifactorial es efectivamente el caso, entonces la probabilidad de que el paciente contraiga la enfermedad se reduce sólo si primos y parientes más lejanos tienen la enfermedad. [13] Si bien las enfermedades heredadas multifactorialmente tienden a ser hereditarias, la herencia no seguirá el mismo patrón que un simple cruce monohíbrido o dihíbrido . [10]
Si se sospecha una causa genética y se sabe poco más sobre la enfermedad, queda por ver exactamente cuántos genes intervienen en la expresión fenotípica de la enfermedad. Una vez que se determina eso, se debe responder a la pregunta: si dos personas tienen los genes necesarios, ¿por qué hay diferencias en la expresión entre ellos? En general, lo que hace que los dos individuos sean diferentes es probable que sean factores ambientales. Debido a la naturaleza compleja de las investigaciones genéticas necesarias para determinar dichos patrones de herencia, esta no suele ser la primera vía de investigación que se elegiría para determinar la etiología. [ cita requerida ]

En el caso de los organismos cuyos genomas se conocen, se podría intentar excluir los genes de la región identificada cuya función se sabe con cierta certeza que no está relacionada con el rasgo en cuestión. Si el genoma no está disponible, puede ser una opción secuenciar la región identificada y determinar las funciones putativas de los genes por su similitud con genes con función conocida, generalmente en otros genomas. Esto se puede hacer utilizando BLAST , una herramienta en línea que permite a los usuarios ingresar una secuencia primaria y buscar secuencias similares dentro de la base de datos BLAST de genes de varios organismos. A menudo no es el gen real subyacente al rasgo fenotípico, sino más bien una región de ADN que está estrechamente vinculada con el gen [14].
Otro interés de los genetistas estadísticos que utilizan el mapeo de QTL es determinar la complejidad de la arquitectura genética subyacente a un rasgo fenotípico. Por ejemplo, pueden estar interesados en saber si un fenotipo está determinado por muchos loci independientes o por unos pocos loci, y si esos loci interactúan. Esto puede proporcionar información sobre cómo puede estar evolucionando el fenotipo. [15]
En un desarrollo reciente, los análisis de QTL clásicos se combinaron con el perfil de expresión génica, es decir, mediante microarreglos de ADN . Dichos QTL de expresión (eQTL) describen elementos que controlan cis y trans la expresión de genes frecuentemente asociados a enfermedades. [16] Se ha descubierto que los efectos epistáticos observados son beneficiosos para identificar el gen responsable mediante una validación cruzada de genes dentro de los loci que interactúan con bases de datos de vías metabólicas y literatura científica . [ cita requerida ]
El método más simple para el mapeo de QTL es el análisis de varianza ( ANOVA , a veces llamado "regresión de marcador") en los loci del marcador. En este método, en un retrocruzamiento, se puede calcular una estadística t para comparar los promedios de los dos grupos de genotipos marcadores . Para otros tipos de cruces (como el intercruzamiento), donde hay más de dos genotipos posibles, se utiliza una forma más general de ANOVA, que proporciona una denominada estadística F. El enfoque ANOVA para el mapeo de QTL tiene tres debilidades importantes. Primero, no recibimos estimaciones separadas de la ubicación de QTL y el efecto de QTL. La ubicación de QTL se indica solo al observar qué marcadores dan las mayores diferencias entre los promedios del grupo de genotipos, y el efecto aparente de QTL en un marcador será menor que el efecto verdadero de QTL como resultado de la recombinación entre el marcador y el QTL. Segundo, debemos descartar individuos cuyos genotipos faltan en el marcador. En tercer lugar, cuando los marcadores están muy espaciados, el QTL puede estar bastante lejos de todos los marcadores, por lo que el poder de detección del QTL disminuirá. [ cita requerida ]
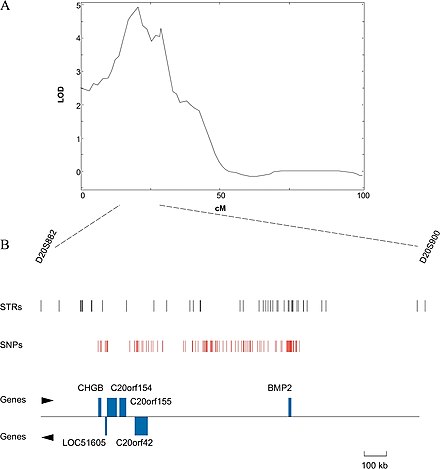
Lander y Botstein desarrollaron el mapeo de intervalos, que supera las tres desventajas del análisis de varianza en los loci marcadores. [17] El mapeo de intervalos es actualmente el enfoque más popular para el mapeo de QTL en cruces experimentales. El método hace uso de un mapa genético de los marcadores tipificados y, al igual que el análisis de varianza, supone la presencia de un solo QTL. En el mapeo de intervalos, cada locus se considera uno a la vez y el logaritmo de la razón de probabilidades ( puntuación LOD ) se calcula para el modelo de que el locus dado es un QTL verdadero. La razón de probabilidades está relacionada con el coeficiente de correlación de Pearson entre el fenotipo y el genotipo marcador para cada individuo en el cruce experimental. [18]
El término "mapeo de intervalos" se utiliza para estimar la posición de un QTL dentro de dos marcadores (a menudo indicados como "marcador-corchete"). El mapeo de intervalos se basa originalmente en la máxima verosimilitud, pero también existen muy buenas aproximaciones posibles con regresión simple. [ cita requerida ]
El principio para el mapeo de QTL es: 1) La probabilidad se puede calcular para un conjunto dado de parámetros (particularmente el efecto QTL y la posición QTL) dados los datos observados sobre fenotipos y genotipos marcadores. 2) Las estimaciones para los parámetros son aquellas donde la probabilidad es más alta. 3) Se puede establecer un umbral de significancia mediante pruebas de permutación. [19]
Los métodos convencionales para la detección de loci de rasgos cuantitativos (QTL) se basan en una comparación de modelos de QTL individuales con un modelo que supone que no hay QTL. Por ejemplo, en el método de "mapeo de intervalos" [20] se evalúa la probabilidad de un único QTL putativo en cada ubicación del genoma. Sin embargo, los QTL ubicados en otras partes del genoma pueden tener un efecto de interferencia. Como consecuencia, el poder de detección puede verse comprometido y las estimaciones de ubicaciones y efectos de los QTL pueden estar sesgadas (Lander y Botstein 1989; Knapp 1991). Incluso pueden aparecer los llamados QTL "fantasma" inexistentes (Haley y Knott 1992; Martinez y Curnow 1992). Por lo tanto, se podrían mapear múltiples QTL de manera más eficiente y precisa utilizando múltiples modelos de QTL. [21] Un enfoque popular para manejar el mapeo de QTL donde múltiples QTL contribuyen a un rasgo es escanear iterativamente el genoma y agregar QTL conocidos al modelo de regresión a medida que se identifican los QTL. Este método, denominado mapeo de intervalo compuesto, determina tanto la ubicación como el tamaño de los efectos de los QTL con mayor precisión que los enfoques de QTL único, especialmente en poblaciones de mapeo pequeñas donde el efecto de la correlación entre genotipos en la población de mapeo puede ser problemático. [ cita requerida ]
En este método, se realiza un mapeo de intervalos utilizando un subconjunto de loci marcadores como covariables. Estos marcadores sirven como sustitutos de otros QTL para aumentar la resolución del mapeo de intervalos, al tener en cuenta los QTL vinculados y reducir la variación residual. El problema clave con CIM se refiere a la elección de loci marcadores adecuados para que sirvan como covariables; una vez que se han elegido, CIM convierte el problema de selección del modelo en un análisis unidimensional. Sin embargo, la elección de covariables de marcadores no se ha resuelto. No es sorprendente que los marcadores adecuados sean los más cercanos a los QTL verdaderos, por lo que si uno pudiera encontrarlos, el problema del mapeo de QTL estaría completo de todos modos.
El mapeo de intervalos compuestos inclusivos (ICIM) también se ha propuesto como un método potencial para el mapeo de QTL. [22]
El mapeo de QTL basado en la familia , o mapeo basado en el pedigrí familiar ( mapeo de ligamiento y asociación ), involucra múltiples familias en lugar de una sola familia. El mapeo de QTL basado en la familia ha sido la única forma de mapear genes donde los cruces experimentales son difíciles de hacer. Sin embargo, debido a algunas ventajas, ahora los genetistas de plantas están intentando incorporar algunos de los métodos pioneros en la genética humana. [23] Se ha discutido el uso del enfoque basado en el pedigrí familiar (Bink et al. 2008). El mapeo de ligamiento y asociación basado en la familia se ha implementado con éxito (Rosyara et al. 2009) [24]
{{cite journal}}: |last13=tiene nombre genérico ( ayuda ) S2CID 195367115.{{cite web}}: CS1 maint: archived copy as title (link)Revista de Ciencias de la Vida, 2008, 161:85–96.