Vibración

Oscilaciones mecánicas alrededor de un punto de equilibrio.

La vibración (del latín vibrō  'sacudir') es un fenómeno mecánico mediante el cual se producen oscilaciones alrededor de un punto de equilibrio . La vibración puede ser determinista si las oscilaciones pueden caracterizarse con precisión (por ejemplo, el movimiento periódico de un péndulo ), o aleatoria si las oscilaciones sólo pueden analizarse estadísticamente (por ejemplo, el movimiento de un neumático en un camino de grava).

La vibración puede ser deseable: por ejemplo, el movimiento de un diapasón , la lengüeta de un instrumento de viento o armónica , un teléfono móvil o el cono de un altavoz .

En muchos casos, sin embargo, la vibración es indeseable, ya que desperdicia energía y crea sonidos no deseados . Por ejemplo, los movimientos vibratorios de motores , motores eléctricos o cualquier dispositivo mecánico en funcionamiento suelen ser no deseados. Estas vibraciones podrían ser causadas por desequilibrios en las piezas giratorias, fricción desigual o el engranaje de los dientes de los engranajes . Los diseños cuidadosos suelen minimizar las vibraciones no deseadas.

Los estudios del sonido y las vibraciones están estrechamente relacionados (ambos pertenecen al grupo de la acústica ). El sonido, u ondas de presión , son generados por estructuras que vibran (por ejemplo, cuerdas vocales ); Estas ondas de presión también pueden inducir la vibración de estructuras (p. ej., tímpano ). Por lo tanto, los intentos de reducir el ruido suelen estar relacionados con cuestiones de vibración. ^[1]

Uno de los posibles modos de vibración de un tambor circular (ver otros modos).

Suspensión de automóviles: El diseño del control de vibraciones se lleva a cabo como parte de la ingeniería acústica , automotriz o mecánica .

Las vibraciones de mecanizado son comunes en el proceso de fabricación sustractiva .

Tipos

La vibración libre o vibración natural ocurre cuando un sistema mecánico se pone en movimiento con una entrada inicial y se le permite vibrar libremente. Ejemplos de este tipo de vibración son tirar de un niño hacia atrás en un columpio y soltarlo, o golpear un diapasón y dejarlo sonar. El sistema mecánico vibra en una o más de sus frecuencias naturales y se amortigua hasta quedar inmóvil.

La vibración forzada se produce cuando se aplica a un sistema mecánico una perturbación que varía en el tiempo (carga, desplazamiento, velocidad o aceleración). La perturbación puede ser una entrada periódica y de estado estable, una entrada transitoria o una entrada aleatoria. La entrada periódica puede ser una perturbación armónica o no armónica. Ejemplos de estos tipos de vibración incluyen el temblor de una lavadora debido a un desequilibrio, la vibración del transporte causada por un motor o una carretera irregular, o la vibración de un edificio durante un terremoto. Para los sistemas lineales, la frecuencia de la respuesta de vibración en estado estacionario resultante de la aplicación de una entrada armónica periódica es igual a la frecuencia de la fuerza o movimiento aplicado, y la magnitud de la respuesta depende del sistema mecánico real.

Vibración amortiguada: cuando la energía de un sistema vibratorio se disipa gradualmente por la fricción y otras resistencias, se dice que las vibraciones están amortiguadas. Las vibraciones se reducen gradualmente o cambian de frecuencia o intensidad o cesan y el sistema descansa en su posición de equilibrio. Un ejemplo de este tipo de vibración es la suspensión vehicular amortiguada por el amortiguador .

Aislamiento

El aislamiento de vibraciones es la prevención de la transmisión de vibraciones de un componente de un sistema a otras partes del mismo sistema, como en edificios o sistemas mecánicos . ^[2] La vibración es indeseable en muchos ámbitos, principalmente en sistemas de ingeniería y espacios habitables, y se han desarrollado métodos para evitar la transferencia de vibraciones a dichos sistemas. Las vibraciones se propagan a través de ondas mecánicas y ciertos enlaces mecánicos conducen las vibraciones de manera más eficiente que otros. El aislamiento pasivo de vibraciones utiliza materiales y enlaces mecánicos que absorben y amortiguan estas ondas mecánicas. El aislamiento activo de vibraciones implica sensores y actuadores que producen interferencias disruptivas que cancelan las vibraciones entrantes.

Pruebas

La prueba de vibración se logra introduciendo una función de fuerza en una estructura, generalmente con algún tipo de agitador. Alternativamente, se adjunta un DUT (dispositivo bajo prueba) a la "mesa" de un agitador. Las pruebas de vibración se realizan para examinar la respuesta de un dispositivo bajo prueba (DUT) a un entorno de vibración definido. La respuesta medida puede ser la capacidad de funcionar en el entorno de vibración, la vida útil, las frecuencias resonantes o la salida de sonido de chirridos y traqueteos ( NVH ). Las pruebas de chirridos y traqueteos se realizan con un tipo especial de agitador silencioso que produce niveles de sonido muy bajos mientras está en funcionamiento.

Para forzar una frecuencia relativamente baja (normalmente menos de 100 Hz), se utilizan agitadores servohidráulicos (electrohidráulicos). Para frecuencias más altas (normalmente de 5 Hz a 2000 Hz), se utilizan agitadores electrodinámicos. Generalmente, uno o más puntos de "entrada" o "control" ubicados en el lado del dispositivo bajo prueba de un dispositivo de vibración se mantienen a una aceleración específica. ^[1] Otros puntos de "respuesta" pueden experimentar niveles de vibración más altos (resonancia) o niveles de vibración más bajos (antirresonancia o amortiguación) que los puntos de control. A menudo es deseable lograr antirresonancia para evitar que un sistema se vuelva demasiado ruidoso o para reducir la tensión en ciertas partes debido a los modos de vibración causados ​​por frecuencias de vibración específicas. ^[3]

Los tipos más comunes de servicios de pruebas de vibraciones realizados por los laboratorios de pruebas de vibraciones son sinusoidales y aleatorios. Se realizan pruebas sinusoidales (una frecuencia a la vez) para estudiar la respuesta estructural del dispositivo bajo prueba (DUT). Durante la historia temprana de las pruebas de vibración, los controladores de las máquinas de vibración se limitaban únicamente a controlar el movimiento sinusoidal, por lo que sólo se realizaban pruebas sinusoidales. Más tarde, controladores analógicos y luego digitales más sofisticados pudieron proporcionar control aleatorio (todas las frecuencias a la vez). Generalmente se considera que una prueba aleatoria (todas las frecuencias a la vez) replica más fielmente un entorno del mundo real, como las entradas de la carretera a un automóvil en movimiento.

La mayoría de las pruebas de vibración se realizan en un "único eje del DUT" a la vez, aunque la mayoría de las vibraciones del mundo real ocurren en varios ejes simultáneamente. MIL-STD-810G, lanzado a finales de 2008, Método de prueba 527, exige pruebas de múltiples excitadores. El dispositivo de prueba de vibración ^[4] utilizado para conectar el DUT a la mesa vibratoria debe estar diseñado para el rango de frecuencia del espectro de prueba de vibración. Es difícil diseñar un dispositivo de prueba de vibración que duplique la respuesta dinámica (impedancia mecánica) ^[5] del montaje real en uso. Por esta razón, para garantizar la repetibilidad entre las pruebas de vibración, los dispositivos de vibración están diseñados para estar libres de resonancia ^[5] dentro del rango de frecuencia de la prueba. Generalmente, para dispositivos más pequeños y rangos de frecuencia más bajos, el diseñador puede apuntar a un diseño de dispositivo que esté libre de resonancias en el rango de frecuencia de prueba. Esto se vuelve más difícil a medida que el DUT aumenta y la frecuencia de las pruebas aumenta. En estos casos, las estrategias de control multipunto ^[6] pueden mitigar algunas de las resonancias que puedan estar presentes en el futuro.

Algunos métodos de prueba de vibración limitan la cantidad de diafonía (movimiento de un punto de respuesta en una dirección mutuamente perpendicular al eje bajo prueba) que puede exhibir el dispositivo de prueba de vibración. Los dispositivos diseñados específicamente para rastrear o registrar vibraciones se denominan vibroscopios .

Análisis

El análisis de vibraciones (VA), aplicado en un entorno industrial o de mantenimiento, tiene como objetivo reducir los costos de mantenimiento y el tiempo de inactividad de los equipos mediante la detección de fallas en los equipos. ^{[7] [8]} VA es un componente clave de un programa de monitoreo de condición (CM) y a menudo se lo conoce como mantenimiento predictivo (PdM). ^[9] Más comúnmente, VA se utiliza para detectar fallas en equipos giratorios (ventiladores, motores, bombas y cajas de engranajes, etc.), como desequilibrio, desalineación, fallas en los rodamientos de elementos rodantes y condiciones de resonancia. ^[10]

VA puede usar las unidades de desplazamiento, velocidad y aceleración mostradas como una forma de onda de tiempo (TWF), pero lo más común es que se use el espectro, derivado de una rápida transformada de Fourier del TWF. El espectro de vibración proporciona información de frecuencia importante que puede identificar el componente defectuoso.

Los fundamentos del análisis de vibraciones se pueden entender estudiando el modelo simple Masa-resorte-amortiguador . De hecho, incluso una estructura compleja como la carrocería de un automóvil puede modelarse como una "suma" de modelos simples de masa, resorte y amortiguador. El modelo masa-resorte-amortiguador es un ejemplo de oscilador armónico simple . Las matemáticas utilizadas para describir su comportamiento son idénticas a las de otros osciladores armónicos simples como el circuito RLC .

Nota: Este artículo no incluye las derivaciones matemáticas paso a paso, pero se centra en las principales ecuaciones y conceptos del análisis de vibraciones. Consulte las referencias al final del artículo para obtener derivaciones detalladas.

Vibración libre sin amortiguación

Modelo de resorte de masa simple

Para comenzar la investigación de la masa-resorte-amortiguador, suponga que la amortiguación es insignificante y que no se aplica ninguna fuerza externa a la masa (es decir, vibración libre). La fuerza aplicada a la masa por el resorte es proporcional a la cantidad que se estira el resorte "x" (suponiendo que el resorte ya está comprimido debido al peso de la masa). La constante de proporcionalidad, k, es la rigidez del resorte y tiene unidades de fuerza/distancia (por ejemplo, lbf/in o N/m). El signo negativo indica que la fuerza siempre se opone al movimiento de la masa que se le atribuye:

${\displaystyle F_{s}=-kx.\!}$

La fuerza generada por la masa es proporcional a la aceleración de la masa dada por la segunda ley del movimiento de Newton :

${\displaystyle \Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}.}$

La suma de las fuerzas sobre la masa genera esta ecuación diferencial ordinaria : ${\displaystyle \ m{\ddot {x}}+kx=0.}$

Movimiento armónico simple del sistema masa-resorte.

Suponiendo que el inicio de la vibración comienza estirando el resorte una distancia de A y soltándolo, la solución a la ecuación anterior que describe el movimiento de la masa es:

${\displaystyle x(t)=A\cos(2\pi f_{n}t).\!}$

Esta solución dice que oscilará con un movimiento armónico simple que tiene una amplitud de A y una frecuencia de f _n . El número f _n se llama frecuencia natural no amortiguada . Para el sistema simple masa-resorte, f _n se define como:

${\displaystyle f_{n}={1 \over {2\pi }}{\sqrt {k \over m}}.\!}$

Nota: la frecuencia angular ω (ω=2 π f ) con unidades de radianes por segundo se usa a menudo en ecuaciones porque simplifica las ecuaciones, pero normalmente se convierte a frecuencia ordinaria (unidades de Hz o ciclos equivalentes por segundo) al expresar la frecuencia de un sistema. Si se conocen la masa y la rigidez del sistema, la fórmula anterior puede determinar la frecuencia a la que el sistema vibra una vez puesto en movimiento por una perturbación inicial. Todo sistema vibratorio tiene una o más frecuencias naturales que vibran al mismo tiempo que se perturban. Esta relación simple se puede utilizar para comprender en general qué le sucede a un sistema más complejo una vez que agregamos masa o rigidez. Por ejemplo, la fórmula anterior explica por qué, cuando un automóvil o camión está completamente cargado, la suspensión se siente "más suave" que sin carga: la masa ha aumentado, lo que reduce la frecuencia natural del sistema.

Qué hace que el sistema vibre: desde el punto de vista de la conservación de la energía

El movimiento vibratorio podría entenderse en términos de conservación de energía . En el ejemplo anterior, el resorte se ha extendido en un valor de x y, por lo tanto, se almacena algo de energía potencial ( ) en el resorte. Una vez liberado, el resorte tiende a volver a su estado no estirado (que es el estado de mínima energía potencial) y en el proceso acelera la masa. En el punto donde el resorte ha alcanzado su estado no estirado, toda la energía potencial que suministramos al estirarlo se ha transformado en energía cinética ( ). Luego, la masa comienza a desacelerar porque ahora está comprimiendo el resorte y en el proceso transfiriendo la energía cinética de nuevo a su potencial. Por tanto, la oscilación del resorte equivale a la transferencia de energía cinética a energía potencial. En este modelo simple, la masa continúa oscilando siempre con la misma magnitud, pero en un sistema real, la amortiguación siempre disipa la energía y, finalmente, hace que el resorte se detenga. ${\displaystyle {\tfrac {1}{2}}kx^{2}}$ ${\displaystyle {\tfrac {1}{2}}mv^{2}}$

Vibración libre con amortiguación.

Modelo masa-resorte-amortiguador

Cuando se agrega un amortiguador "viscoso" al modelo, se genera una fuerza que es proporcional a la velocidad de la masa. La amortiguación se llama viscosa porque modela los efectos de un fluido dentro de un objeto. La constante de proporcionalidad c se llama coeficiente de amortiguación y tiene unidades de fuerza sobre velocidad (lbf⋅s/in o N⋅s/m).

${\displaystyle F_{\text{d}}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}.}$

La suma de las fuerzas sobre la masa da como resultado la siguiente ecuación diferencial ordinaria:

${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0.}$

La solución de esta ecuación depende de la cantidad de amortiguamiento. Si la amortiguación es lo suficientemente pequeña, el sistema aún vibra, pero eventualmente, con el tiempo, deja de hacerlo. Este caso se llama subamortiguación, que es importante en el análisis de vibraciones. Si la amortiguación se aumenta justo hasta el punto en que el sistema ya no oscila, el sistema ha alcanzado el punto de amortiguación crítica . Si la amortiguación aumenta más allá de la amortiguación crítica, el sistema está sobreamortiguado . El valor que debe alcanzar el coeficiente de amortiguamiento para un amortiguamiento crítico en el modelo masa-resorte-amortiguador es:

${\displaystyle c_{\text{c}}=2{\sqrt {\text{km}}}.}$

Para caracterizar la cantidad de amortiguamiento en un sistema se utiliza una relación llamada relación de amortiguamiento (también conocida como factor de amortiguamiento y % de amortiguamiento crítico). Esta relación de amortiguación es solo una relación entre la amortiguación real y la cantidad de amortiguación necesaria para alcanzar la amortiguación crítica. La fórmula para la relación de amortiguación ( ) del modelo masa-resorte-amortiguador es: ${\displaystyle \zeta }$

${\displaystyle \zeta ={c \over 2{\sqrt {\text{km}}}}.}$

Por ejemplo, las estructuras metálicas (por ejemplo, fuselajes de aviones, cigüeñales de motores) tienen factores de amortiguación inferiores a 0,05, mientras que las suspensiones de automóviles están en el rango de 0,2 a 0,3. La solución al sistema subamortiguado para el modelo masa-resorte-amortiguador es la siguiente:

${\displaystyle x(t)=Xe^{-\zeta \omega _{n}t}\cos \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t-\phi \right),\qquad \omega _{n}=2\pi f_{n}.}$

Vibración libre con relación de amortiguación de 0,1 y 0,3

El valor de X , la magnitud inicial y el cambio de fase están determinados por la cantidad de estiramiento del resorte. Las fórmulas para estos valores se pueden encontrar en las referencias. ${\displaystyle \phi ,}$

Frecuencias naturales amortiguadas y no amortiguadas

Los puntos principales a tener en cuenta de la solución son el término exponencial y la función coseno. El término exponencial define la rapidez con la que el sistema se “amortigua”: cuanto mayor sea la relación de amortiguación, más rápido se amortiguará hasta cero. La función coseno es la porción oscilante de la solución, pero la frecuencia de las oscilaciones es diferente a la del caso no amortiguado.

La frecuencia en este caso se denomina "frecuencia natural amortiguada" y se relaciona con la frecuencia natural no amortiguada mediante la siguiente fórmula: ${\displaystyle f_{\text{d}},}$

${\displaystyle f_{\text{d}}=f_{n}{\sqrt {1-\zeta ^{2}}}.}$

La frecuencia natural amortiguada es menor que la frecuencia natural no amortiguada, pero en muchos casos prácticos la relación de amortiguamiento es relativamente pequeña y, por tanto, la diferencia es insignificante. Por lo tanto, la descripción amortiguada y no amortiguada a menudo se omite al indicar la frecuencia natural (por ejemplo, con una relación de amortiguamiento de 0,1, la frecuencia natural amortiguada es sólo un 1% menor que la no amortiguada).

Los gráficos al lado presentan cómo las relaciones de amortiguación de 0,1 y 0,3 afectan la forma en que el sistema "suena" con el tiempo. Lo que se hace a menudo en la práctica es medir experimentalmente la vibración libre después de un impacto (por ejemplo, con un martillo) y luego determinar la frecuencia natural del sistema midiendo la tasa de oscilación, así como la relación de amortiguación midiendo la tasa de oscilación. decadencia. La frecuencia natural y la relación de amortiguación no sólo son importantes en la vibración libre, sino que también caracterizan cómo se comporta un sistema bajo vibración forzada.

^[11]

Vibración forzada con amortiguación.

El comportamiento del modelo de amortiguador de masa de resorte varía con la adición de una fuerza armónica. Una fuerza de este tipo podría generarse, por ejemplo, mediante un desequilibrio giratorio.

${\displaystyle F=F_{0}\sin(2\pi ft).\!}$

La suma de las fuerzas sobre la masa da como resultado la siguiente ecuación diferencial ordinaria:

${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F_{0}\sin(2\pi ft).}$

La solución en estado estacionario de este problema se puede escribir como:

${\displaystyle x(t)=X\sin(2\pi ft+\phi ).\!}$

El resultado establece que la masa oscilará a la misma frecuencia, f , de la fuerza aplicada, pero con un cambio de fase. ${\displaystyle \phi .}$

La amplitud de la vibración “X” está definida por la siguiente fórmula.

${\displaystyle X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}.}$

Donde "r" se define como la relación entre la frecuencia de la fuerza armónica y la frecuencia natural no amortiguada del modelo masa-resorte-amortiguador.

${\displaystyle r={\frac {f}{f_{n}}}.}$

El cambio de fase se define mediante la siguiente fórmula. ${\displaystyle \phi ,}$

${\displaystyle \phi =\arctan \left({\frac {-2\zeta r}{1-r^{2}}}\right).}$

La gráfica de estas funciones, denominada "respuesta de frecuencia del sistema", presenta una de las características más importantes de la vibración forzada. En un sistema ligeramente amortiguado, cuando la frecuencia forzada se acerca a la frecuencia natural ( ), la amplitud de la vibración puede volverse extremadamente alta. Este fenómeno se llama resonancia (por lo tanto, la frecuencia natural de un sistema a menudo se denomina frecuencia de resonancia). En los sistemas de rodamientos de rotor, cualquier velocidad de rotación que excite una frecuencia resonante se denomina velocidad crítica . ${\displaystyle r\approx 1}$

Si se produce resonancia en un sistema mecánico, puede ser muy perjudicial y provocar un fallo final del sistema. En consecuencia, una de las razones principales para el análisis de vibraciones es predecir cuándo puede ocurrir este tipo de resonancia y luego determinar qué pasos tomar para evitar que ocurra. Como muestra el gráfico de amplitud, agregar amortiguación puede reducir significativamente la magnitud de la vibración. Además, la magnitud se puede reducir si la frecuencia natural se puede alejar de la frecuencia de forzamiento cambiando la rigidez o la masa del sistema. Si no se puede cambiar el sistema, quizás se pueda cambiar la frecuencia de forzado (por ejemplo, cambiando la velocidad de la máquina que genera la fuerza).

Los siguientes son algunos otros puntos con respecto a la vibración forzada que se muestran en los gráficos de respuesta de frecuencia.

• En una relación de frecuencia dada, la amplitud de la vibración, X , es directamente proporcional a la amplitud de la fuerza (por ejemplo, si se duplica la fuerza, la vibración se duplica) ${\displaystyle F_{0}}$
• Con poca o ninguna amortiguación, la vibración está en fase con la frecuencia forzada cuando la relación de frecuencia r  < 1 y 180 grados desfasada cuando la relación de frecuencia r  > 1
• Cuando r  ≪ 1, la amplitud es solo la deflexión del resorte bajo la fuerza estática. Esta deflexión se llama deflexión estática. Por lo tanto, cuando r  ≪ 1 los efectos del amortiguador y la masa son mínimos. ${\displaystyle F_{0}.}$ ${\displaystyle \delta _{st}.}$
• Cuando r  ≫ 1, la amplitud de la vibración es en realidad menor que la deflexión estática. En esta región, la fuerza generada por la masa ( F  =  ma ) domina porque la aceleración vista por la masa aumenta con la frecuencia. Dado que la deflexión observada en el resorte, X , se reduce en esta región, la fuerza transmitida por el resorte ( F  =  kx ) a la base se reduce. Por lo tanto, el sistema masa-resorte-amortiguador aísla la fuerza armónica de la base de montaje, lo que se conoce como aislamiento de vibraciones . En realidad, una mayor amortiguación reduce los efectos del aislamiento de vibraciones cuando r  ≫ 1 porque la fuerza de amortiguación ( F  =  cv ) también se transmite a la base. ${\displaystyle \delta _{st}.}$
• Cualquiera que sea la amortiguación, la vibración está desfasada 90 grados con la frecuencia forzada cuando la relación de frecuencia r  = 1, lo cual es muy útil cuando se trata de determinar la frecuencia natural del sistema.
• Cualquiera que sea la amortiguación, cuando r  ≫ 1, la vibración está desfasada 180 grados con la frecuencia de forzamiento.
• Cualquiera que sea la amortiguación, cuando r  ≪ 1, la vibración está en fase con la frecuencia de forzamiento.

Causas de resonancia

La resonancia es fácil de entender si el resorte y la masa se consideran elementos de almacenamiento de energía: la masa almacena energía cinética y el resorte almacena energía potencial. Como se analizó anteriormente, cuando la masa y el resorte no tienen ninguna fuerza externa que actúe sobre ellos, transfieren energía de un lado a otro a una velocidad igual a la frecuencia natural. En otras palabras, para bombear energía de manera eficiente tanto a la masa como al resorte se requiere que la fuente de energía alimente la energía a una velocidad igual a la frecuencia natural. Aplicar una fuerza a la masa y al resorte es similar a empujar a un niño en un columpio, se necesita un empujón en el momento correcto para que el columpio suba cada vez más. Como en el caso del columpio, la fuerza aplicada no necesita ser alta para lograr grandes movimientos, sino que simplemente debe agregar energía al sistema.

El amortiguador, en lugar de almacenar energía, la disipa. Dado que la fuerza de amortiguación es proporcional a la velocidad, cuanto mayor es el movimiento, más energía disipa el amortiguador. Por lo tanto, hay un punto en el que la energía disipada por el amortiguador es igual a la energía agregada por la fuerza. En este punto, el sistema ha alcanzado su amplitud máxima y seguirá vibrando a este nivel mientras la fuerza aplicada siga siendo la misma. Si no existe amortiguación, no hay nada que disipe la energía y, teóricamente, el movimiento seguirá creciendo hasta el infinito.

Aplicación de fuerzas "complejas" al modelo masa-resorte-amortiguador

En una sección anterior sólo se aplicó al modelo una fuerza armónica simple, pero esto se puede ampliar considerablemente utilizando dos poderosas herramientas matemáticas. La primera es la transformada de Fourier que toma una señal en función del tiempo ( dominio del tiempo ) y la descompone en sus componentes armónicos en función de la frecuencia ( dominio de la frecuencia ). Por ejemplo, aplicando una fuerza al modelo masa-resorte-amortiguador que se repite el siguiente ciclo: una fuerza igual a 1  newton durante 0,5 segundos y luego ninguna fuerza durante 0,5 segundos. Este tipo de fuerza tiene la forma de una onda cuadrada de 1 Hz .

Cómo se puede representar una onda cuadrada de 1 Hz como una suma de ondas sinusoidales (armónicos) y el espectro de frecuencia correspondiente. Haga clic y vaya a resolución completa para ver una animación.

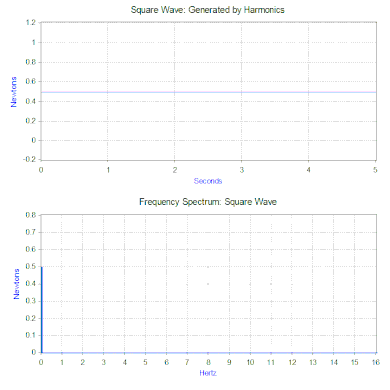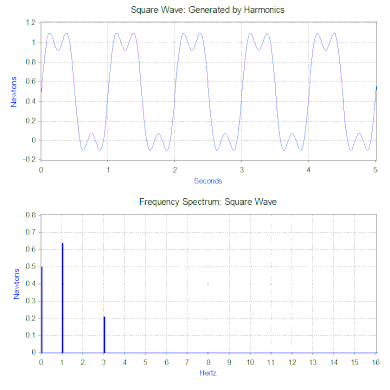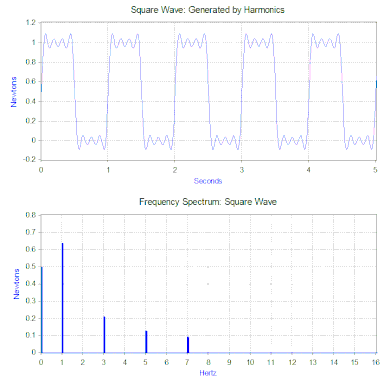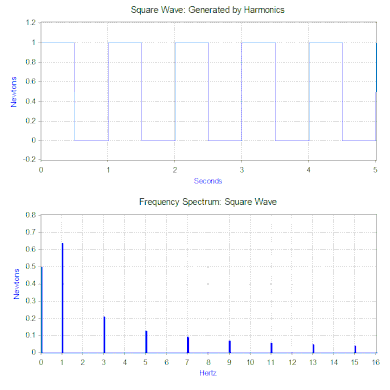
La transformada de Fourier de la onda cuadrada genera un espectro de frecuencia que presenta la magnitud de los armónicos que componen la onda cuadrada (la fase también se genera, pero normalmente es menos preocupante y, por lo tanto, a menudo no se representa). La transformada de Fourier también se puede utilizar para analizar funciones no periódicas como transitorios (por ejemplo, impulsos) y funciones aleatorias. La transformada de Fourier casi siempre se calcula utilizando el algoritmo informático de transformada rápida de Fourier (FFT) en combinación con una función de ventana .

En el caso de nuestra fuerza de onda cuadrada, el primer componente es en realidad una fuerza constante de 0,5 newton y está representado por un valor de 0 Hz en el espectro de frecuencia. El siguiente componente es una onda sinusoidal de 1 Hz con una amplitud de 0,64. Esto se muestra mediante la línea a 1 Hz. Los componentes restantes tienen frecuencias impares y se necesita una cantidad infinita de ondas sinusoidales para generar la onda cuadrada perfecta. Por lo tanto, la transformada de Fourier permite interpretar la fuerza como una suma de fuerzas sinusoidales aplicadas en lugar de una fuerza más "compleja" (por ejemplo, una onda cuadrada).

En la sección anterior, la solución de vibración se dio para una sola fuerza armónica, pero la transformada de Fourier en general proporciona múltiples fuerzas armónicas. La segunda herramienta matemática, el principio de superposición , permite la suma de las soluciones de múltiples fuerzas si el sistema es lineal . En el caso del modelo resorte-masa-amortiguador, el sistema es lineal si la fuerza del resorte es proporcional al desplazamiento y la amortiguación es proporcional a la velocidad en el rango de movimiento de interés. Por tanto, la solución al problema de una onda cuadrada es sumar la vibración predicha de cada una de las fuerzas armónicas encontradas en el espectro de frecuencias de la onda cuadrada.

Modelo de respuesta de frecuencia

La solución de un problema de vibración puede verse como una relación entrada/salida, donde la fuerza es la entrada y la salida es la vibración. Representar la fuerza y ​​la vibración en el dominio de la frecuencia (magnitud y fase) permite la siguiente relación:

${\displaystyle X(i\omega )=H(i\omega )\cdot F(i\omega ){\text{ or }}H(i\omega )={X(i\omega ) \over F(i\omega )}.}$

${\displaystyle H(i\omega )}$se llama función de respuesta de frecuencia (también conocida como función de transferencia , pero técnicamente no es tan precisa) y tiene un componente de magnitud y fase (si se representa como un número complejo , un componente real e imaginario). La magnitud de la función de respuesta en frecuencia (FRF) se presentó anteriormente para el sistema masa-resorte-amortiguador.

${\displaystyle |H(i\omega )|=\left|{X(i\omega ) \over F(i\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},{\text{ where }}r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}.}$

La fase del FRF también se presentó anteriormente como:

${\displaystyle \angle H(i\omega )=-\arctan \left({\frac {2\zeta r}{1-r^{2}}}\right).}$

Modelo de respuesta de frecuencia

Por ejemplo, calcular el FRF para un sistema masa-resorte-amortiguador con una masa de 1 kg, una rigidez del resorte de 1,93 N/mm y una relación de amortiguación de 0,1. Los valores del resorte y la masa dan una frecuencia natural de 7 Hz para este sistema específico. La aplicación de la onda cuadrada de 1 Hz anterior permite calcular la vibración predicha de la masa. La figura ilustra la vibración resultante. Sucede en este ejemplo que el cuarto armónico de la onda cuadrada cae a 7 Hz. Por lo tanto, la respuesta de frecuencia de la masa-resorte-amortiguador produce una vibración alta de 7 Hz, aunque la fuerza de entrada tenía un armónico relativamente bajo de 7 Hz. Este ejemplo destaca que la vibración resultante depende tanto de la función de forzado como del sistema al que se aplica la fuerza.

La figura también muestra la representación en el dominio del tiempo de la vibración resultante. Esto se hace realizando una transformada de Fourier inversa que convierte datos en el dominio de la frecuencia al dominio del tiempo. En la práctica, esto rara vez se hace porque el espectro de frecuencias proporciona toda la información necesaria.

La función de respuesta de frecuencia (FRF) no necesariamente tiene que calcularse a partir del conocimiento de la masa, el amortiguamiento y la rigidez del sistema, pero puede medirse experimentalmente. Por ejemplo, si se aplica una fuerza conocida en un rango de frecuencias y si se miden las vibraciones asociadas, se puede calcular la función de respuesta de frecuencia, caracterizando así el sistema. Esta técnica se utiliza en el campo del análisis modal experimental para determinar las características de vibración de una estructura.

Múltiples grados de sistemas de libertad y formas de modo.

Modelo de dos grados de libertad

El modelo simple masa-resorte-amortiguador es la base del análisis de vibraciones. El modelo descrito anteriormente se llama modelo de un solo grado de libertad (SDOF), ya que se supone que la masa solo se mueve hacia arriba y hacia abajo. En sistemas más complejos, el sistema debe discretizarse en más masas que se mueven en más de una dirección, agregando grados de libertad. Los conceptos principales de múltiples grados de libertad (MDOF) se pueden entender observando solo un modelo de dos grados de libertad como se muestra en la figura.

Las ecuaciones de movimiento del sistema 2DOF son:

${\displaystyle m_{1}{\ddot {x_{1}}}+(c_{1}+c_{2}){\dot {x_{1}}}-c_{2}{\dot {x_{2}}}+(k_{1}+k_{2})x_{1}-k_{2}x_{2}=f_{1},}$

${\displaystyle m_{2}{\ddot {x_{2}}}-c_{2}{\dot {x_{1}}}+(c_{2}+c_{3}){\dot {x_{2}}}-k_{2}x_{1}+(k_{2}+k_{3})x_{2}=f_{2}.\!}$

Esto se puede reescribir en formato matricial :

${\displaystyle {\begin{bmatrix}m_{1}&0\\0&m_{2}\end{bmatrix}}{\begin{Bmatrix}{\ddot {x_{1}}}\\{\ddot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}c_{1}+c_{2}&-c_{2}\\-c_{2}&c_{2}+c_{3}\end{bmatrix}}{\begin{Bmatrix}{\dot {x_{1}}}\\{\dot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\end{bmatrix}}{\begin{Bmatrix}x_{1}\\x_{2}\end{Bmatrix}}={\begin{Bmatrix}f_{1}\\f_{2}\end{Bmatrix}}.}$

Una forma más compacta de esta ecuación matricial se puede escribir como:

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}C\end{bmatrix}}{\begin{Bmatrix}{\dot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}f\end{Bmatrix}}}$

donde y son matrices simétricas denominadas respectivamente matrices de masa, amortiguamiento y rigidez. Las matrices son matrices cuadradas NxN donde N es el número de grados de libertad del sistema. ${\displaystyle {\begin{bmatrix}M\end{bmatrix}},}$ ${\displaystyle {\begin{bmatrix}C\end{bmatrix}},}$ ${\displaystyle {\begin{bmatrix}K\end{bmatrix}}}$

El siguiente análisis involucra el caso donde no hay amortiguación ni fuerzas aplicadas (es decir, vibración libre). La solución de un sistema viscosamente amortiguado es algo más complicada. ^[12]

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}=0.}$

Esta ecuación diferencial se puede resolver suponiendo el siguiente tipo de solución:

${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}.}$

Nota: Usar la solución exponencial de es un truco matemático que se usa para resolver ecuaciones diferenciales lineales. Usando la fórmula de Euler y tomando solo la parte real de la solución, es la misma solución en coseno para el sistema 1 DOF. La solución exponencial sólo se utiliza porque es más fácil de manipular matemáticamente. ${\displaystyle {\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}}$

La ecuación entonces queda:

${\displaystyle {\begin{bmatrix}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}=0.}$

Como no puede ser igual a cero, la ecuación se reduce a lo siguiente. ${\displaystyle e^{i\omega t}}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.}$

Problema de valores propios

Esto se conoce como un problema de valores propios en matemáticas y se puede poner en el formato estándar multiplicando previamente la ecuación por ${\displaystyle {\begin{bmatrix}M\end{bmatrix}}^{-1}}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0}$

y si: y ${\displaystyle {\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}A\end{bmatrix}}}$ ${\displaystyle \lambda =\omega ^{2}\,}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}A\end{bmatrix}}-\lambda {\begin{bmatrix}I\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.}$

La solución al problema da como resultado N valores propios (es decir ), donde N corresponde al número de grados de libertad. Los valores propios proporcionan las frecuencias naturales del sistema. Cuando estos valores propios se sustituyen nuevamente en el conjunto original de ecuaciones, los valores que corresponden a cada valor propio se denominan vectores propios . Estos vectores propios representan las formas modales del sistema. La solución de un problema de valores propios puede ser bastante engorrosa (especialmente para problemas con muchos grados de libertad), pero afortunadamente la mayoría de los programas de análisis matemático tienen rutinas de valores propios. ${\displaystyle \omega _{1}^{2},\omega _{2}^{2},\cdots \omega _{N}^{2}}$ ${\displaystyle {\begin{Bmatrix}X\end{Bmatrix}}}$

Los valores propios y vectores propios suelen escribirse en el siguiente formato matricial y describen el modelo modal del sistema:

${\displaystyle {\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}\omega _{1}^{2}&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &\omega _{N}^{2}\end{bmatrix}}{\text{ and }}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\cdots {\begin{Bmatrix}\psi _{N}\end{Bmatrix}}\end{bmatrix}}.}$

Un ejemplo sencillo que utiliza el modelo de 2 grados de libertad puede ayudar a ilustrar los conceptos. Supongamos que ambas masas tienen una masa de 1 kg y la rigidez de los tres resortes es igual a 1000 N/m. Las matrices de masa y rigidez para este problema son entonces:

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}}$y ${\displaystyle {\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.}$

Entonces ${\displaystyle {\begin{bmatrix}A\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.}$

Los valores propios para este problema dados por una rutina de valores propios son:

${\displaystyle {\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}1000&0\\0&3000\end{bmatrix}}.}$

Las frecuencias naturales en las unidades de hercios son entonces (recordando ) y ${\displaystyle \scriptstyle \omega =2\pi f}$ ${\displaystyle \scriptstyle f_{1}=5.033\mathrm {\ Hz} }$ ${\displaystyle \scriptstyle f_{2}=8.717{\text{ Hz}}.}$

Las dos formas modales para las respectivas frecuencias naturales se dan como:

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}-0.707\\-0.707\end{Bmatrix}}_{1}{\begin{Bmatrix}0.707\\-0.707\end{Bmatrix}}_{2}\end{bmatrix}}.}$

Dado que el sistema es un sistema de 2 DOF, existen dos modos con sus respectivas frecuencias y formas naturales. Los vectores de forma modal no son el movimiento absoluto, sino que simplemente describen el movimiento relativo de los grados de libertad. En nuestro caso, el primer vector de forma modo dice que las masas se mueven juntas en fase ya que tienen el mismo valor y signo. En el caso del vector de forma del segundo modo, cada masa se mueve en dirección opuesta a la misma velocidad.

Ilustración de un problema de múltiples grados de libertad

Cuando hay muchos grados de libertad, un método para visualizar las formas modales es animarlas utilizando software de análisis estructural como Femap , ANSYS o VA One de ESI Group . En la siguiente figura se muestra un ejemplo de animación de formas de modo para una viga en I en voladizo , como se demuestra mediante el análisis modal en ANSYS. En este caso, se utilizó el método de los elementos finitos para generar una aproximación de las matrices de masa y rigidez mallando el objeto de interés para resolver un problema de valores propios discretos . Tenga en cuenta que, en este caso, el método de los elementos finitos proporciona una aproximación de la superficie mallada (para la cual existe un número infinito de modos y frecuencias de vibración). Por lo tanto, este modelo relativamente simple que tiene más de 100 grados de libertad y, por lo tanto, tantas frecuencias naturales y formas modales, proporciona una buena aproximación para las primeras frecuencias y modos naturales ^† . Generalmente, sólo los primeros modos son importantes para aplicaciones prácticas.

^ Tenga en cuenta que al realizar una aproximación numérica de cualquier modelo matemático, se debe determinar la convergencia de los parámetros de interés.

Problema de múltiples DOF ​​convertido en un solo problema de DOF

Los vectores propios tienen propiedades muy importantes llamadas propiedades de ortogonalidad. Estas propiedades se pueden utilizar para simplificar enormemente la solución de modelos de múltiples grados de libertad. Se puede demostrar que los vectores propios tienen las siguientes propiedades:

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}},}$

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}.}$

${\displaystyle {\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}}$y son matrices diagonales que contienen los valores modales de masa y rigidez para cada uno de los modos. (Nota: dado que los vectores propios (formas modales) se pueden escalar arbitrariamente, las propiedades de ortogonalidad se usan a menudo para escalar los vectores propios de modo que el valor de masa modal para cada modo sea igual a 1. Por lo tanto, la matriz de masa modal es una matriz de identidad ) ${\displaystyle {\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}}$

Estas propiedades se pueden utilizar para simplificar enormemente la solución de modelos de múltiples grados de libertad realizando la siguiente transformación de coordenadas.

${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}.}$

El uso de esta transformación de coordenadas en la ecuación diferencial de vibración libre original da como resultado la siguiente ecuación.

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Aprovechando las propiedades de ortogonalidad premultiplicando esta ecuación por ${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}}$

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Las propiedades de ortogonalidad luego simplifican esta ecuación a:

${\displaystyle {\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Esta ecuación es la base del análisis de vibraciones para sistemas de múltiples grados de libertad. Se puede derivar un tipo de resultado similar para sistemas amortiguados. ^[12] La clave es que las matrices modales de masa y rigidez son matrices diagonales y por lo tanto las ecuaciones han sido "desacopladas". En otras palabras, el problema se ha transformado de un problema grande y difícil de manejar con múltiples grados de libertad a muchos problemas de un solo grado de libertad que pueden resolverse utilizando los mismos métodos descritos anteriormente.

Resolver x se reemplaza por resolver q , lo que se conoce como coordenadas modales o factores de participación modal.

Puede ser más claro de entender si está escrito como: ${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}}$

${\displaystyle {\begin{Bmatrix}x_{n}\end{Bmatrix}}=q_{1}{\begin{Bmatrix}\psi \end{Bmatrix}}_{1}+q_{2}{\begin{Bmatrix}\psi \end{Bmatrix}}_{2}+q_{3}{\begin{Bmatrix}\psi \end{Bmatrix}}_{3}+\cdots +q_{N}{\begin{Bmatrix}\psi \end{Bmatrix}}_{N}.}$

Escrito de esta forma se puede ver que la vibración en cada uno de los grados de libertad es simplemente una suma lineal de las formas modales. Además, cuánto "participa" cada modo en la vibración final está definido por q, su factor de participación modal.

Modo de cuerpo rígido

Un sistema de múltiples grados de libertad sin restricciones experimenta tanto traslación como/o rotación y vibración del cuerpo rígido. La existencia de un modo de cuerpo rígido da como resultado una frecuencia natural cero. La forma modal correspondiente se denomina modo de cuerpo rígido.

Ver también

• ingeniería acústica
• Compuesto antivibración
• máquina equilibradora
• Aislamiento básico
• Amortiguación
• velocidad critica
• Relación de amortiguación
• El método de Dunkerley.
• Ingeniería Sísmica
• Péndulo elástico
• Transformada rápida de Fourier
• Ingeniería Mecánica
• resonancia mecánica
• Análisis modal
• Forma de modo
• Ruido y vibraciones en los buques marítimos.
• Ruido, vibración y aspereza.
• palestesia
• Compensación pasiva de elevación
• Péndulo
• Vibración cuántica
• Vibración aleatoria
• Calidad de conducción
• El cociente de Rayleigh en el análisis de vibraciones.
• Agitador (dispositivo de prueba)
• Choque
• Registrador de datos de golpes y vibraciones
• Oscilador armónico simple
• Sonido
• Acústica estructural
• Dinámica estructural
• Equilibrio de neumáticos
• Vibración torsional
• Amortiguador de masa sintonizado
• Calibrador de vibraciones
• control de vibraciones
• Aislamiento de vibraciones
• Ola
• Vibración de todo el cuerpo

Referencias

1. Tustin, Wayne. Dónde colocar el acelerómetro de control: una de las decisiones más críticas en el desarrollo de ensayos de vibración aleatoria también es la más descuidada , EE-Evaluación Ingeniería, 2006
2. Escudier, Marcel; Atkins, Tony (2019). Diccionario de ingeniería mecánica (2 ed.). Prensa de la Universidad de Oxford. doi :10.1093/acref/9780198832102.001.0001. ISBN 978-0-19-883210-2.
3. "Polytec InFocus 1/2007" (PDF) . Archivado desde el original (PDF) el 24 de julio de 2019 . Consultado el 24 de julio de 2019 .
4. Tony Araujo. La evolución de los dispositivos de vibración para automóviles , EE-Evaluación Ingeniería, 2019
5. Blanks, HS, "Técnicas de equivalencia para pruebas de vibración", Notas SVIC, pág.17.
6. Araujo, T. y Yao, B., "Calificación del rendimiento de dispositivos de vibración: una revisión de las mejores prácticas de la industria automotriz", documento técnico de SAE 2020-01-1065, 2020, https://doi.org/10.4271/2020-01 -1065.
7. Crawford, arte; Manual simplificado de análisis de vibraciones
8. Eshleman, R 1999, Vibraciones básicas de maquinaria: una introducción a las pruebas, análisis y monitoreo de máquinas.
9. Instituto Mobius; Analista de Vibraciones Categoría 2 – Notas del Curso 2013
10. "Importancia del análisis de vibraciones en el mantenimiento". 2021-01-05 . Consultado el 8 de enero de 2021 .
11. Simionescu, PA (2014). Herramientas de simulación y gráficos asistidas por computadora para usuarios de AutoCAD (1ª ed.). Boca Ratón, FL: CRC Press. ISBN 978-1-4822-5290-3.
12. Maia, Silva. Análisis modal teórico y experimental , Research Studies Press Ltd., 1997, ISBN 0-471-97067-0 

Otras lecturas

• Lengua, Benson, Principios de vibración , Oxford University Press, 2001, ISBN 0-19-514246-2 
• Inman, Daniel J., Ingeniería de vibraciones , Prentice Hall, 2001, ISBN 0-13-726142-X 
• Thompson, WT, Teoría de las vibraciones , Nelson Thornes Ltd, 1996, ISBN 0-412-78390-8 
• Hartog, Den, Vibraciones mecánicas , Publicaciones de Dover, 1985, ISBN 0-486-64785-4 
• Reynolds, Douglas D. (2016). Principios de ingeniería de la vibración mecánica (4ª ed.). Bloomington, Indiana, EE.UU.: Trafford On Demand Publishing. pag. 485.ISBN _ 978-1-4907-1437-0.
• [1]
• Instituto de Seguridad y Salud en el Trabajo del Seguro Social Alemán de Accidentes : Vibración de cuerpo entero y mano-brazo
• Manarikkal, I., Elsaha, F., Mba, D. y Laila, D. Modelado dinámico de cajas de engranajes planetarias con dientes agrietados mediante análisis de vibraciones, (2019) Avances en el monitoreo de la condición de maquinaria en operaciones no estacionarias, páginas 240–250 , Springer, Suiza; [2]

enlaces externos

• Hojas de Excel gratuitas para estimar parámetros modales
• Referencia de análisis de vibraciones - Instituto Mobius
• Monitoreo de condición y protección de maquinaria – Siemens AG