Álgebra C* de dimensión aproximadamente finita

Álgebra C*

En matemáticas , una C*-álgebra de dimensión finita (AF) aproximada es una C*-álgebra que es el límite inductivo de una secuencia de C*-álgebras de dimensión finita . La dimensionalidad finita aproximada fue definida y descrita por primera vez de manera combinatoria por Ola Bratteli . Más tarde, George A. Elliott dio una clasificación completa de las álgebras AF utilizando el funtor K ₀ cuyo rango consiste en grupos abelianos ordenados con una estructura de orden suficientemente agradable.

El teorema de clasificación para las álgebras AF sirve como prototipo para los resultados de clasificación para clases más grandes de C*-álgebras separables, simples, estables y finitas. Su prueba se divide en dos partes. El invariante aquí es K ₀ con su estructura de orden natural; este es un funtor . Primero, se prueba la existencia : un homomorfismo entre invariantes debe elevarse a un *-homomorfismo de álgebras. Segundo, se muestra unicidad : la elevación debe ser única hasta una equivalencia unitaria aproximada. La clasificación se sigue entonces de lo que se conoce como el argumento de entrelazamiento . Para las álgebras AF unitarias, tanto la existencia como la unicidad se siguen del hecho de que el semigrupo de proyecciones de Murray-von Neumann en un álgebra AF es cancelativo.

La contraparte de las álgebras AF C* simples en el mundo del álgebra de von Neumann son los factores hiperfinitos, que fueron clasificados por Connes y Haagerup .

En el contexto de la geometría y topología no conmutativa , las C*-álgebras AF son generalizaciones no conmutativas de C ₀ ( X ), donde X es un espacio metrizable totalmente desconectado .

Definición y propiedades básicas

Álgebras C* de dimensión finita

Un C*-álgebra A de dimensión finita arbitraria toma la siguiente forma, salvo isomorfismo:

${\displaystyle \oplus _{k}M_{n_{k}},}$

donde M _i denota el álgebra matricial completa de matrices i × i .

Hasta la equivalencia unitaria, un *-homomorfismo unitario Φ : M _i → M _j es necesariamente de la forma

${\displaystyle \Phi (a)=a\otimes I_{r},}$

donde r · i = j . Se dice que el número r es la multiplicidad de Φ. En general, un homomorfismo unital entre C*-álgebras de dimensión finita

${\displaystyle \Phi :\oplus _{1}^{s}M_{n_{k}}\rightarrow \oplus _{1}^{t}M_{m_{l}}}$

se especifica, hasta la equivalencia unitaria, por una matriz t × s de multiplicidades parciales ( r _{l k} ) que satisface, para todo l

${\displaystyle \sum _{k}r_{lk}n_{k}=m_{l}.\;}$

En el caso no unitario, la igualdad se reemplaza por ≤. Gráficamente, Φ, equivalentemente ( r _{l k} ), se puede representar mediante su diagrama de Bratteli . El diagrama de Bratteli es un grafo dirigido con nodos correspondientes a cada n _k y m _l y el número de flechas desde n _k hasta m _l es la multiplicidad parcial r _lk .

Consideremos la categoría cuyos objetos son clases de isomorfismo de C*-álgebras de dimensión finita y cuyos morfismos son *-homomorfismos módulo equivalencia unitaria. Según la discusión anterior, los objetos pueden verse como vectores con entradas en N y los morfismos son las matrices de multiplicidad parcial.

Álgebras AF

El AC*-álgebra es AF si es el límite directo de una secuencia de C*-álgebras de dimensión finita:

${\displaystyle A=\varinjlim \cdots \rightarrow A_{i}\,{\stackrel {\alpha _{i}}{\rightarrow }}A_{i+1}\rightarrow \cdots ,}$

donde cada A _i es una C*-álgebra de dimensión finita y las funciones conexas α _i son *-homomorfismos. Supondremos que cada α _i es unital. El sistema inductivo que especifica una álgebra AF no es único. Siempre se puede derivar a una subsucesión. Suprimiendo las funciones conexas, A también se puede escribir como

${\displaystyle A={\overline {\cup _{n}A_{n}}}.}$

El diagrama de Bratteli de A se forma a partir de los diagramas de Bratteli de { α _i } de la manera obvia. Por ejemplo, el triángulo de Pascal , con los nodos conectados por flechas hacia abajo apropiadas, es el diagrama de Bratteli de un álgebra AF. A la derecha se muestra un diagrama de Bratteli del álgebra CAR . Las dos flechas entre los nodos significan que cada mapa de conexión es una incrustación de multiplicidad 2.

${\displaystyle 1\rightrightarrows 2\rightrightarrows 4\rightrightarrows 8\rightrightarrows \dots }$

(Un diagrama de Bratteli del álgebra CAR)

Si un álgebra AF A = ​​(∪ _n A _n ) ⁻ , entonces un ideal J en A toma la forma ∪ _n ( J ​​∩ A _n ) ⁻ . En particular, J es en sí mismo un álgebra AF. Dado un diagrama de Bratteli de A y algún subconjunto S de nodos, el subdiagrama generado por S da un sistema inductivo que especifica un ideal de A . De hecho, todo ideal surge de esta manera.

Debido a la presencia de unidades matriciales en la secuencia inductiva, las álgebras AF tienen la siguiente caracterización local: un C*-álgebra A es AF si y solo si A es separable y cualquier subconjunto finito de A está "casi contenido" en alguna C*-subálgebra de dimensión finita.

Las proyecciones en ∪ _n A _n de hecho forman una unidad aproximada de A .

Es evidente que la extensión de un álgebra C* de dimensión finita por otra álgebra C* de dimensión finita es de nuevo de dimensión finita. En términos más generales, la extensión de un álgebra AF por otra álgebra AF es de nuevo AF. ^[1]

Clasificación

K0

El grupo K-teórico K ₀ es un invariante de las C*-álgebras. Tiene su origen en la K-teoría topológica y sirve como rango de una especie de "función dimensional". Para un álgebra AF A , K ₀ ( A ) se puede definir de la siguiente manera. Sea M _n ( A ) la C*-álgebra de matrices n × n cuyas entradas son elementos de A . M _n ( A ) se puede incrustar en M _{n + 1} ( A ) canónicamente, en la "esquina superior izquierda". Considérese el límite directo algebraico

${\displaystyle M_{\infty }(A)=\varinjlim \cdots \rightarrow M_{n}(A)\rightarrow M_{n+1}(A)\rightarrow \cdots .}$

Denotemos las proyecciones (idempotentes autoadjuntos) en esta álgebra por P ( A ). Se dice que dos elementos p y q son equivalentes de Murray-von Neumann , denotados por p ~ q , si p = vv* y q = v*v para alguna isometría parcial v en M _∞ ( A ). Está claro que ~ es una relación de equivalencia. Definamos una operación binaria + en el conjunto de equivalencias P ( A )/~ por

${\displaystyle [p]+[q]=[p\oplus q]}$

donde ⊕ da como resultado la suma directa ortogonal de dos matrices de dimensión finita correspondientes a p y q . Si bien podríamos elegir matrices de dimensión arbitrariamente grande para reemplazar a p y q , nuestro resultado será equivalente de todos modos. Esto hace que P ( A )/~ sea un semigrupo que tiene la propiedad de cancelación . Denotamos este semigrupo por K ₀ ( A ) ⁺ . Realizar la construcción del grupo de Grothendieck da como resultado un grupo abeliano, que es K ₀ ( A ).

K ₀ ( A ) tiene una estructura de orden natural: decimos [ p ] ≤ [ q ] si p es equivalente de Murray-von Neumann a una subproyección de q . Esto hace que K ₀ ( A ) sea un grupo ordenado cuyo cono positivo es K ₀ ( A ) ⁺ .

Por ejemplo, para un álgebra C* de dimensión finita

${\displaystyle A=\oplus _{k=1}^{m}M_{n_{k}},}$

Uno tiene

${\displaystyle (K_{0}(A),K_{0}(A)^{+})=(\mathbb {Z} ^{m},\mathbb {Z} _{+}^{m}).}$

Dos características esenciales de la función A ↦ K ₀ ( A ) son:

1. K _{0 es un} funtor (covariante) . Un *-homomorfismo α  : A → B entre álgebras AF induce un homomorfismo de grupo α _*  : K ₀ ( A ) → K ₀ ( B ). En particular, cuando A y B son ambos de dimensión finita, α _* puede identificarse con la matriz de multiplicidades parciales de α .
2. K ₀ respeta límites directos. Si A = ∪ _n α _n ( A _n ) ⁻ , entonces K ₀ ( A ) es el límite directo ∪ _n α _{n *} ( K ₀ ( A _n )).

El grupo de dimensiones

Como M _∞ ( M _∞ ( A )) es isomorfo a M _∞ ( A ), K ₀ solo puede distinguir álgebras AF hasta isomorfismo estable . Por ejemplo, M ₂ y M ₄ no son isomorfos sino isomorfos estables; K ₀ ( M ₂ ) = K ₀ ( M ₄ ) = Z .

Se necesita un invariante más fino para detectar clases de isomorfismo. Para un álgebra AF A , definimos la escala de K ₀ ( A ), denotada por Γ( A ), como el subconjunto cuyos elementos están representados por proyecciones en A :

${\displaystyle \Gamma (A)=\{[p]\,|\,p^{*}=p^{2}=p\in A\}.}$

Cuando A es unital con unidad 1 _A , el elemento K ₀ [1 _A ] es el elemento máximo de Γ( A ) y de hecho,

${\displaystyle \Gamma (A)=\{x\in K_{0}(A)\,|\,0\leq x\leq [1_{A}]\}.}$

El triple ( K ₀ , K ₀ ⁺ , Γ( A )) se llama grupo de dimensión de A . Si A = M _s , su grupo de dimensión es ( Z , Z ⁺ , {1, 2,..., s }).

Se dice que un homomorfismo de grupo entre grupos dimensionales es contractivo si preserva la escala. Se dice que dos grupos dimensionales son isomorfos si existe un isomorfismo de grupo contractivo entre ellos.

El grupo de dimensión conserva las propiedades esenciales de K ₀ :

1. Un *-homomorfismo α  : A → B entre álgebras AF induce de hecho un homomorfismo de grupo contractivo α _* en los grupos de dimensión. Cuando A y B son ambos de dimensión finita, correspondientes a cada matriz de multiplicidades parciales ψ , existe un único, hasta equivalencia unitaria, *-homomorfismo α  : A → B tal que α _* = ψ .
2. Si A = ∪ _n α _n ( A _n ) ⁻ , entonces el grupo de dimensión de A es el límite directo de los de A _n .

Teorema de Elliott

Diagramas conmutativos para el teorema de Elliott.

El teorema de Elliott dice que el grupo de dimensión es un invariante completo de las álgebras AF: dos álgebras AF A y B son isomorfas si y sólo si sus grupos de dimensión son isomorfas.

Se necesitan dos hechos preliminares antes de poder esbozar una prueba del teorema de Elliott. El primero resume la discusión anterior sobre las C*-álgebras de dimensión finita.

Lema Para dos C*-álgebras A y B de dimensión finita , y un homomorfismo contractivo ψ : K ₀ ( A ) → K ₀ ( B ), existe un *-homomorfismo φ : A → B tal que φ _* = ψ , y φ es único hasta equivalencia unitaria.

El lema puede extenderse al caso en que B es AF. Una función ψ en el nivel de K ₀ puede "retroceder", en el nivel de las álgebras, a alguna etapa finita en el sistema inductivo.

Lema Sea A finito-dimensional y B AF, B = (∪ _n B _n ) ⁻ . Sea β _m el homomorfismo canónico de B _m en B . Entonces, para cualquier homomorfismo contractivo ψ : K ₀ ( A ) → K ₀ ( B ), existe un *-homomorfismo φ : A → B _m tal que β _m* φ _* = ψ , y φ es único hasta equivalencia unitaria en B .

La demostración del lema se basa en la simple observación de que K ₀ ( A ) es finitamente generado y, puesto que K ₀ respeta límites directos, K ₀ ( B ) = ∪ _n β _n* K ₀ ( B _n ).

Teorema (Elliott) Dos álgebras AF A y B son isomorfas si y solo si sus grupos de dimensión ( K ₀ ( A ), K ₀ ⁺ ( A ), Γ( A )) y ( K ₀ ( B ), K ₀ ⁺ ( B ), Γ( B )) son isomorfos.

El quid de la prueba se conoce como el argumento entrelazado de Elliott . Dado un isomorfismo entre grupos de dimensión, se construye un diagrama de triángulos conmutativos entre los sistemas directos de A y B aplicando el segundo lema.

Esbozamos la prueba de la parte no trivial del teorema, correspondiente a la secuencia de diagramas conmutativos de la derecha.

Sea Φ: ( K ₀ ( A ), K ₀ ⁺ ( A ), Γ( A )) → ( K ₀ ( B ), K ₀ ⁺ ( B ), Γ( B )) un isomorfismo de grupo de dimensión.

1. Considérese la composición de mapas Φ α _1*  : K ₀ ( A ₁ ) → K ₀ ( B ). Por el lema anterior, existe B ₁ y un *-homomorfismo φ ₁ : A ₁ → B ₁ tal que el primer diagrama de la derecha conmuta.
2. El mismo argumento aplicado a β _1* Φ ⁻¹ muestra que el segundo diagrama conmuta para algún A ₂ .
3. Comparando los diagramas 1 y 2 se obtiene el diagrama 3.
4. Utilizando la propiedad del límite directo y moviendo A ₂ más abajo si es necesario, obtenemos el diagrama 4, un triángulo conmutativo en el nivel de K ₀ .
5. Para álgebras de dimensión finita, dos *-homomorfismos inducen la misma función en K ₀ si y solo si son unitariamente equivalentes. Por lo tanto, al componer ψ ₁ con una conjugación unitaria si es necesario, tenemos un triángulo conmutativo en el nivel de álgebras.
6. Por inducción, tenemos un diagrama de triángulos conmutativos como el indicado en el último diagrama. La función φ : A → B es el límite directo de la sucesión { φ _n }. Sea ψ : B → A el límite directo de la sucesión { ψ _n }. Está claro que φ y ψ son inversas mutuas. Por lo tanto, A y B son isomorfos.

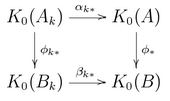
Además, en el nivel de K ₀ , el diagrama adyacente conmuta para cada k . Por unicidad del límite directo de las funciones, φ _* = Φ.

El teorema de Effros-Handelman-Shen

El grupo de dimensión de un álgebra AF es un grupo de Riesz . El teorema de Effros-Handelman-Shen dice que lo inverso es cierto. Todo grupo de Riesz, con una escala dada, surge como el grupo de dimensión de algún álgebra AF. Esto especifica el rango del funtor de clasificación K ₀ para las álgebras AF y completa la clasificación.

Grupos de Riesz

Un grupo G con un orden parcial se llama grupo ordenado . El conjunto G ⁺ de elementos ≥ 0 se llama cono positivo de G. Se dice que G no está perforado si k · g ∈ G ⁺ implica g ∈ G ⁺ .

La siguiente propiedad se llama propiedad de descomposición de Riesz : si x , y _i ≥ 0 y x ≤ Σ y _i , entonces existe x _i ≥ 0 tal que x = Σ x _i , y x _i ≤ y _i para cada i .

Un grupo de Riesz ( G , G ⁺ ) es un grupo ordenado que no está perforado y tiene la propiedad de descomposición de Riesz.

Está claro que si A es de dimensión finita, ( K ₀ , K ₀ ⁺ ) es un grupo de Riesz, donde Z ^k tiene orden de entrada dado. Las dos propiedades de los grupos de Riesz se conservan mediante límites directos, suponiendo que la estructura de orden en el límite directo proviene de aquellas en el sistema inductivo. Por lo tanto, ( K ₀ , K ₀ ⁺ ) es un grupo de Riesz para un álgebra AF A .

Un paso clave hacia el teorema de Effros-Handelman-Shen es el hecho de que cada grupo de Riesz es el límite directo de Z ^k , cada uno con la estructura de orden canónico. Esto depende del siguiente lema técnico, a veces denominado criterio de Shen en la literatura.

El criterio de Shen.

Lema Sea ( G , G ⁺ ) un grupo de Riesz, ϕ : ( Z ^k , Z ^k ₊ ) → ( G , G ⁺ ) un homomorfismo positivo. Entonces existen funciones σ y ψ , como se indica en el diagrama adyacente, tales que ker( σ ) = ker( ϕ ).

Corolario Todo grupo de Riesz ( G , G ⁺ ) puede expresarse como un límite directo

${\displaystyle (G,G^{+})=\varinjlim (\mathbb {Z} ^{n_{k}},\mathbb {Z} _{+}^{n_{k}}),}$

donde todos los homomorfismos de conexión en el sistema dirigido en el lado derecho son positivos.

El teorema

Teorema Si ( G , G ⁺ ) es un grupo de Riesz contable con escala Γ( G ), entonces existe un álgebra AF A tal que ( K ₀ , K ₀ ⁺ , Γ( A )) = ( G , G ⁺ , Γ( G )). En particular, si Γ( G ) = [0, u _G ] con elemento maximalista u _G , entonces A es unital con [1 _A ] = [ u _G ].

Consideremos primero el caso especial donde Γ( G ) = [0, u _G ] con elemento máximo u _G . Supongamos

${\displaystyle (G,G^{+})=\varinjlim (H_{k},H_{k}^{+}),\quad {\mbox{where}}\quad (H,H_{k}^{+})=(\mathbb {Z} ^{n_{k}},\mathbb {Z} _{+}^{n_{k}}).}$

Pasando a una subsecuencia si es necesario, dejemos

${\displaystyle \Gamma (H_{1})=\{v\in H_{1}^{+}|\phi _{1}(v)\in \Gamma (G)\},}$

donde φ ₁ ( u ₁ ) = u _G para algún elemento u ₁ . Ahora considere el ideal de orden G ₁ generado por u ₁ . Debido a que cada H ₁ tiene la estructura de orden canónica, G ₁ es una suma directa de Z (con el número de copias posibles menor que el de H ₁ ). Por lo tanto, esto da un álgebra de dimensión finita A ₁ cuyo grupo de dimensión es ( G ₁ G ₁ ⁺ , [0, u ₁ ]). A continuación, avance u ₁ definiendo u ₂ = φ ₁₂ ( u ₁ ). Nuevamente, u ₂ determina un álgebra de dimensión finita A ₂ . Hay un homomorfismo correspondiente α ₁₂ tal que α _12* = φ ₁₂ . La inducción da un sistema dirigido

${\displaystyle A=\varinjlim A_{k},}$

cuyo K ₀ es

${\displaystyle \varinjlim (G_{k},G_{k}^{+}),}$

con escala

${\displaystyle \cup _{k}\phi _{k}[0,u_{k}]=[0,u_{G}].}$

Esto demuestra el caso especial.

En general, se aplica un argumento similar. Obsérvese que la escala es, por definición, un conjunto dirigido . Si Γ( G ) = { v _k }, se puede elegir u _k ∈ Γ( G ) tal que u _k ≥ v ₁ ... v _k . El mismo argumento que el anterior demuestra el teorema.

Ejemplos

Por definición, las álgebras uniformemente hiperfinitas son AF y unital. Sus grupos de dimensión son los subgrupos de Q . Por ejemplo, para las matrices 2 × 2 M ₂ , K ₀ ( M ₂ ) es el grupo de números racionales de la forma ⁠a/2⁠ para a en Z . La escala es Γ( M ₂ ) = {0, ⁠1/2⁠ , 1}. Para el álgebra CAR A , K ₀ ( A ) es el grupo de racionales diádicos con escala K ₀ ( A ) ∩ [0, 1], con 1 = [1 _A ]. Todos estos grupos son simples , en un sentido apropiado para grupos ordenados. Por lo tanto, las álgebras UHF son C*-álgebras simples. En general, los grupos que no son densos en Q son los grupos de dimensión de M _k para algún k .

Las C*-álgebras conmutativas, que fueron caracterizadas por Gelfand , son AF precisamente cuando el espectro está totalmente desconectado . ^[2] Las funciones continuas C ( X ) en el conjunto de Cantor X son un ejemplo de ello.

Programa de clasificación de Elliott

Elliott propuso que otras clases de C*-álgebras pueden clasificarse mediante invariantes K-teóricos. Para una C*-álgebra A , el invariante de Elliott se define como

${\displaystyle {\mbox{Ell}}(A)=((K_{0}(A),K_{0}(A)^{+},\Gamma (A)),K_{1}(A),T^{+}(A),\rho _{A}),}$

donde son los funcionales lineales positivos trazales en la topología débil-*, y es el emparejamiento natural entre y . ${\displaystyle T^{+}(A)}$ ${\displaystyle \rho _{A}}$ ${\displaystyle T^{+}(A)}$ ${\displaystyle K_{0}(A)}$

La conjetura original de Elliott establecía que el invariante de Elliott clasifica C*-álgebras unitarias separables y susceptibles simples.

En la literatura se pueden encontrar varias conjeturas de este tipo con sus correspondientes invariantes de Elliott modificados/refinados.

Álgebras de von Neumann

En un contexto relacionado, un álgebra de von Neumann de dimensión aproximadamente finita o hiperfinita es una con un predual separable y que contiene un AF C*-álgebra débilmente densa. Murray y von Neumann demostraron que, hasta el isomorfismo, existe un único factor hiperfinito de tipo II _1. Connes obtuvo el resultado análogo para el factor II _∞ . Powers exhibió una familia de factores hiperfinitos de tipo III no isomorfos con cardinalidad del continuo. Hoy tenemos una clasificación completa de factores hiperfinitos.

Notas

1. Lawrence G. Brown. Extensiones de álgebras AF: el problema de elevación de proyecciones. Álgebras de operadores y aplicaciones, Actas de simposios sobre matemáticas puras, vol. 38, Parte 1, págs. 175-176, American Mathematical Soc., 1982
2. Davidson 1996, pág. 77.

Referencias

• Bratteli, Ola. (1972), Límites inductivos de C*-álgebras de dimensión finita , Trans. Amer. Math. Soc. 171 , 195-234.
• Davidson, KR (1996), C*-álgebras por ejemplo , Field Institute Monographs 6 , American Mathematical Society.
• Effros, EG , Handelman, DE y Shen CL (1980), Grupos de dimensión y sus representaciones afines , Amer. J. Math. 102 , 385-402.
• Elliott, GA (1976), Sobre la clasificación de límites inductivos de secuencias de álgebras de dimensión finita semisimples , J. Algebra 38 , 29-44.
• Elliott, GA y Toms, AS (2008), Propiedades de regularidad en el programa de clasificación para C-álgebras separables y susceptibles , Bull. Amer. Math. Soc. 45 , 229-245.
• Fillmore, PA (1996), Guía del usuario para álgebras de operadores , Wiley-Interscience.
• Rørdam, M. (2002), Clasificación de C*-álgebras nucleares , Enciclopedia de Ciencias Matemáticas 126 , Springer-Verlag.

Enlaces externos

• "Álgebra AF", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]