Lóbulo de Roche

En astronomía , el lóbulo de Roche es la región que rodea a una estrella en un sistema binario dentro de la cual el material que orbita está ligado gravitacionalmente a esa estrella. Es una región con forma similar a una lágrima, limitada por un potencial gravitatorio crítico , con el vértice de la lágrima apuntando hacia la otra estrella (el vértice está en el punto lagrangiano L 1 del sistema).

El lóbulo de Roche es diferente de la esfera de Roche , que se aproxima a la esfera de influencia gravitatoria de un cuerpo astronómico frente a las perturbaciones de un cuerpo más masivo alrededor del cual orbita. También es diferente del límite de Roche , que es la distancia a la que un objeto que se mantiene unido solo por la gravedad comienza a romperse debido a las fuerzas de marea . El lóbulo de Roche, el límite de Roche y la esfera de Roche reciben su nombre del astrónomo francés Édouard Roche .

Definición

Representación tridimensional del potencial de Roche en una estrella binaria con una relación de masas de 2, en el marco de referencia co-rotativo. Las figuras con forma de gotitas en el diagrama equipotencial en la parte inferior de la figura definen lo que se consideran los lóbulos de Roche de las estrellas. L 1 , L 2 y L 3 son los puntos de Lagrange donde las fuerzas (consideradas en el marco de referencia rotatorio) se cancelan. La masa puede fluir a través del punto de silla L 1 desde una estrella a su compañera, si la estrella llena su lóbulo de Roche. ^[1]

Modelo 3D STL del potencial de Roche de dos cuerpos en órbita, representado mitad como superficie y mitad como malla

En un sistema binario con una órbita circular, suele ser útil describir el sistema en un sistema de coordenadas que gira junto con los objetos. En este marco no inercial , se debe considerar la fuerza centrífuga además de la gravedad. Las dos juntas se pueden describir mediante un potencial , de modo que, por ejemplo, las superficies estelares se encuentran a lo largo de superficies equipotenciales.

Cerca de cada estrella, las superficies de igual potencial gravitatorio son aproximadamente esféricas y concéntricas con la estrella más cercana. Lejos del sistema estelar, los equipotenciales son aproximadamente elipsoidales y alargados paralelos al eje que une los centros estelares. Un equipotencial crítico se intersecta a sí mismo en el punto lagrangiano L 1 del sistema, formando una figura de ocho de dos lóbulos con una de las dos estrellas en el centro de cada lóbulo. Este equipotencial crítico define los lóbulos de Roche. ^[2]

Cuando la materia se mueve con respecto al marco co-rotativo, parecerá que actúa sobre ella una fuerza de Coriolis . Esto no se puede derivar del modelo del lóbulo de Roche, ya que la fuerza de Coriolis es una fuerza no conservativa (es decir, no se puede representar mediante un potencial escalar ).

Análisis adicional

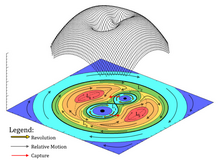
En los gráficos de potencial de gravedad, L ₁ , L ₂ , L ₃ , L ₄ , L ₅ están en rotación sincrónica con el sistema. Las regiones de color rojo, naranja, amarillo, verde, azul claro y azul son conjuntos de potenciales de mayor a menor. Las flechas rojas son la rotación del sistema y las flechas negras son los movimientos relativos de los escombros.

Los desechos se desplazan más rápido en la región de menor potencial y más lento en la de mayor potencial. Por lo tanto, los movimientos relativos de los desechos en la órbita inferior siguen la misma dirección que la revolución del sistema, mientras que en la órbita superior son opuestos.

L ₁ es el punto de equilibrio de captura gravitacional. Es un punto de corte de la gravedad del sistema estelar binario. Es el equilibrio potencial mínimo entre L ₁ , L ₂ , L ₃ , L ₄ y L ₅ . Es la forma más fácil para que los escombros viajen entre una esfera de Hill (un círculo interior de azul y celeste) y regiones de gravedad comunales (ochos de amarillo y verde en el lado interior).

Esfera de colina y órbita de herradura

L ₂ y L ₃ son puntos de equilibrio de perturbación gravitacional. Al pasar por estos dos puntos de equilibrio, los desechos pueden desplazarse entre la región externa (ochos amarillos y verdes en el lado exterior) y la región de gravedad común del sistema binario.

L ₄ y L ₅ son los puntos de potencial máximo del sistema. Son equilibrios inestables. Si la relación de masas de las dos estrellas se hace mayor, las regiones naranja, amarilla y verde se convertirán en una órbita en forma de herradura .

La región roja se convertirá en la órbita del renacuajo .

Transferencia de masa

Cuando una estrella "sobrepasa su lóbulo de Roche", su superficie se extiende más allá de su lóbulo de Roche y el material que se encuentra fuera del lóbulo de Roche puede "caer" al lóbulo de Roche del otro objeto a través del primer punto de Lagrange. En la evolución binaria, esto se conoce como transferencia de masa por desbordamiento del lóbulo de Roche .

En principio, la transferencia de masa podría llevar a la desintegración total del objeto, ya que una reducción de la masa del objeto hace que su lóbulo de Roche se encoja. Sin embargo, hay varias razones por las que esto no sucede en general. En primer lugar, una reducción de la masa de la estrella donante puede hacer que esta también se encoja, posiblemente impidiendo tal resultado. En segundo lugar, con la transferencia de masa entre los dos componentes binarios, también se transfiere momento angular . Mientras que la transferencia de masa de un donante más masivo a un acretor menos masivo generalmente conduce a una órbita que se encoge, lo inverso hace que la órbita se expanda (suponiendo que se conservan la masa y el momento angular). La expansión de la órbita binaria conducirá a una contracción menos dramática o incluso a una expansión del lóbulo de Roche del donante, a menudo impidiendo la destrucción del donante.

Para determinar la estabilidad de la transferencia de masa y, por lo tanto, el destino exacto de la estrella donante, es necesario tener en cuenta cómo reaccionan el radio de la estrella donante y el de su lóbulo de Roche a la pérdida de masa del donante; si la estrella se expande más rápido que su lóbulo de Roche o se contrae menos rápidamente que su lóbulo de Roche durante un tiempo prolongado, la transferencia de masa será inestable y la estrella donante puede desintegrarse. Si la estrella donante se expande menos rápidamente o se contrae más rápido que su lóbulo de Roche, la transferencia de masa generalmente será estable y puede continuar durante mucho tiempo.

La transferencia de masa debida al desbordamiento del lóbulo de Roche es responsable de una serie de fenómenos astronómicos, incluidos los sistemas Algol , las novas recurrentes ( estrellas binarias que consisten en una gigante roja y una enana blanca que están lo suficientemente cerca como para que el material de la gigante roja caiga sobre la enana blanca), las binarias de rayos X y los púlsares de milisegundos . Esta transferencia de masa por desbordamiento del lóbulo de Roche (RLOF) se divide además en tres casos distintos:

Caso A: Caso A RLOF ocurre cuando la estrella donante está quemando hidrógeno . Según Nelson y Eggleton, hay varias subclases ^[3] que se reproducen aquí:
AD dinámico: Cuando se produce una RLOF en una estrella con una zona de convección profunda , la transferencia de masa se produce rápidamente en la escala de tiempo dinámica de la estrella y puede terminar con una fusión completa .
Contacto rápido AR: Similar a AD, pero a medida que la estrella sobre la que se acumula materia rápidamente gana masa, gana tamaño físico suficiente para alcanzar su propio lóbulo de Roche. En esos casos, el sistema se manifiesta como un sistema binario de contacto , como una variable W Ursae Majoris .
AS contacto lento: Similar a la AR, pero solo ocurre un período corto de transferencia rápida de masa seguido de un período mucho más largo de transferencia lenta de masa. Finalmente, las estrellas entrarán en contacto, pero habrán cambiado sustancialmente para cuando esto suceda. Las variables de Algol son el resultado de tales situaciones.
AE adelantamiento temprano: Similar a AS, pero la estrella que gana masa supera a la estrella que dona masa para evolucionar más allá de la secuencia principal. La estrella donante puede encogerse tanto que detenga la transferencia de masa, pero eventualmente la transferencia de masa comenzará nuevamente a medida que la evolución estelar continúa, lo que lleva a los casos
Adelantamiento tardío de AL: el caso en el que la estrella que inicialmente fue donante experimenta una supernova después de que la otra estrella haya experimentado su propia ronda de RLOF.
Sistema binario AB: el caso en el que las estrellas cambian de una a otra, entre las cuales una está experimentando RLOF al menos tres veces (técnicamente, una subclase de lo anterior).
AN no adelantar: el caso cuando la estrella que inicialmente fue donante experimenta una supernova antes de que la otra estrella alcance una fase RLOF.
Gigante agrícola: La transferencia de masa no comienza hasta que la estrella alcanza la rama gigante roja , sino antes de que haya agotado su núcleo de hidrógeno (después de lo cual el sistema se describe como Caso B).
Caso B: El caso B ocurre cuando la RLOF comienza mientras el donante es una estrella que quema hidrógeno post-núcleo/quema de capa de hidrógeno. Este caso se puede subdividir en las clases Br y Bc ^[4] según si la transferencia de masa ocurre desde una estrella dominada por una zona de radiación (Br) y por lo tanto evoluciona como la situación con la mayoría de las RLOF del Caso A o una zona convectiva (Bc) después de la cual puede ocurrir una fase de envoltura común (similar al Caso C). ^[5] Una división alternativa de los casos es Ba, Bb y Bc que corresponden aproximadamente a las fases de RLOF que ocurren durante la fusión de helio, después de la fusión de helio pero antes de la fusión de carbono, o después de la fusión de carbono en la estrella altamente evolucionada. ^[6]
Caso C: El caso C ocurre cuando la RLOF comienza cuando el donante se encuentra en la fase de combustión de la capa de helio o más allá de ella. Estos sistemas son los que se observan con menos frecuencia, pero esto puede deberse a un sesgo de selección . ^[7]

Geometría

La forma precisa del lóbulo de Roche depende de la relación de masas y debe evaluarse numéricamente. Sin embargo, para muchos propósitos es útil aproximar el lóbulo de Roche como una esfera del mismo volumen. Una fórmula aproximada para el radio de esta esfera es $q=M_{1}/M_{2}$

{\frac {r_{1}}{A}}=\max {[f_{1},f_{2}]}

, para

0<q<20

donde y . La función es mayor que para . La longitud A es la separación orbital del sistema y r ₁ es el radio de la esfera cuyo volumen se aproxima al lóbulo de Roche de masa M ₁ . Esta fórmula tiene una precisión de aproximadamente el 2%. ^[2] Eggleton propuso otra fórmula aproximada que se lee de la siguiente manera: $f_{1}=0.38+0.2\log {q}$ $f_{2}=0.46224\left({\frac {q}{1+q}}\right)^{1/3}$ $f_{1}$ $f_{2}$ $q\gtrsim 0.5228$

{\frac {r_{1}}{A}}={\frac {0.49q^{2/3}}{0.6q^{2/3}+\ln(1+q^{1/3})}}

Esta fórmula proporciona resultados con una precisión de hasta el 1 % en todo el rango de la relación de masas . ^[8] $q$

Referencias

^ Fuente
^ ab Paczynski, B. (1971). "Procesos evolutivos en sistemas binarios cerrados". Revista anual de astronomía y astrofísica . 9 : 183–208. Bibcode :1971ARA&A...9..183P. doi :10.1146/annurev.aa.09.090171.001151.
^ Nelson, CA; Eggleton, PP (2001). "Un estudio completo de la evolución binaria del caso A con comparación con los sistemas de tipo Algol observados". The Astrophysical Journal . 552 (2): 664–678. arXiv : astro-ph/0009258 . Bibcode :2001ApJ...552..664N. doi :10.1086/320560. S2CID 119505485.
^ Vanbeveren, D.; Mennekens, N. (1 de abril de 2014). "Fusiones masivas de objetos compactos dobles: fuentes de ondas gravitacionales y sitios de producción de elementos del proceso r". Astronomía y astrofísica . 564 : A134. arXiv : 1307.0959 . Bibcode :2014A&A...564A.134M. doi : 10.1051/0004-6361/201322198 . ISSN 0004-6361.
^ Vanbeveren, D.; Rensbergen, W. van; Loore, C. de (30 de noviembre de 2001). Los binarios más brillantes. Medios de ciencia y negocios de Springer. ISBN 9781402003769.
^ Bhattacharya, D; van den Heuvel, EP J (1991-05-01). "Formación y evolución de pulsares de radio binarios y de milisegundos". Physics Reports . 203 (1): 1–124. Bibcode :1991PhR...203....1B. doi :10.1016/0370-1573(91)90064-S. ISSN 0370-1573.
^ Podsiadlowski, Philipp (febrero de 2014). "La evolución de los sistemas binarios". Procesos de acreción en astrofísica . pp. 45–88. doi :10.1017/CBO9781139343268.003. ISBN 9781139343268. Recuperado el 12 de agosto de 2019 . {{cite book}}: |website=ignorado ( ayuda )
^ Eggleton, PP (1 de mayo de 1983). "Aproximaciones a los radios de los lóbulos de Roche". The Astrophysical Journal . 268 : 368. Bibcode :1983ApJ...268..368E. doi :10.1086/160960.

Fuentes

Morris, SL (febrero de 1994). "Dos expansiones matemáticas de las equipotenciales de Roche". Publicaciones de la Sociedad Astronómica del Pacífico . 106 (696): 154–155. Bibcode :1994PASP..106..154M. doi :10.1086/133361. JSTOR 40680260. S2CID 121386366.
Morris, SL (1 de agosto de 1999). "Los límites de inclinación para eclipses parciales de estrellas binarias". Astrophysical Journal . 520 (2): 797–804. Bibcode :1999ApJ...520..797M. doi : 10.1086/307488 .

Enlaces externos

De Júpiter calientes a supertierras a través del desbordamiento del lóbulo de Roche - Universidad de Cornell