En lógica e informática , el problema de satisfacibilidad booleano (a veces llamado problema de satisfacibilidad proposicional y abreviado SATISFIABILITY , SAT o B-SAT ) es el problema de determinar si existe una interpretación que satisfaga una fórmula booleana determinada . En otras palabras, pregunta si las variables de una fórmula booleana determinada se pueden reemplazar consistentemente por los valores VERDADERO o FALSO de tal manera que la fórmula se evalúe como VERDADERO. Si este es el caso, la fórmula se llama satisfactible . Por otro lado, si no existe tal asignación, la función expresada por la fórmula es FALSA para todas las posibles asignaciones de variables y la fórmula es insatisfactoria . Por ejemplo, la fórmula " a Y NO b " es satisfactoria porque se pueden encontrar los valores a = VERDADERO y b = FALSO, lo que hace que ( a Y NO b ) = VERDADERO. Por el contrario, " a AND NOT a " es insatisfactorio.
SAT es el primer problema que demostró ser NP-completo ; ver teorema de Cook-Levin . Esto significa que todos los problemas de la clase de complejidad NP , que incluye una amplia gama de problemas de optimización y decisión natural, son como mucho tan difíciles de resolver como SAT. No existe ningún algoritmo conocido que resuelva eficientemente cada problema del SAT y, en general, se cree que no existe tal algoritmo; sin embargo, esta creencia no se ha demostrado matemáticamente, y resolver la cuestión de si SAT tiene un algoritmo de tiempo polinomial es equivalente al problema P versus NP , que es un famoso problema abierto en la teoría de la computación.
Sin embargo, a partir de 2007, los algoritmos heurísticos SAT son capaces de resolver casos de problemas que involucran decenas de miles de variables y fórmulas que constan de millones de símbolos, [1] lo cual es suficiente para muchos problemas prácticos SAT de, por ejemplo, inteligencia artificial , diseño de circuitos. , [2] y demostración automática de teoremas .
Una fórmula lógica proposicional , también llamada expresión booleana , se construye a partir de variables , operadores Y ( conjunción , también denotada por ∧), O ( disyunción , ∨), NO ( negación , ¬) y paréntesis. Se dice que una fórmula es satisfactoria si se puede hacer VERDADERA asignando valores lógicos apropiados (es decir, VERDADERO, FALSO) a sus variables. El problema booleano de satisfacibilidad (SAT) consiste, dada una fórmula, en comprobar si es satisfacible. Este problema de decisión es de importancia central en muchas áreas de la informática , incluida la informática teórica , la teoría de la complejidad , [3] [4] algorítmica , criptografía [5] [6] e inteligencia artificial . [7] [ se necesitan citas adicionales ]
Un literal es una variable (en cuyo caso se llama literal positivo ) o la negación de una variable (llamada literal negativo ). Una cláusula es una disyunción de literales (o un solo literal). Una cláusula se llama cláusula de Horn si contiene como máximo un literal positivo. Una fórmula está en forma normal conjuntiva (CNF) si es una conjunción de cláusulas (o una sola cláusula).
Por ejemplo, x 1 es un literal positivo, ¬ x 2 es un literal negativo, x 1 ∨ ¬ x 2 es una cláusula. La fórmula ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 está en forma normal conjuntiva; sus cláusulas primera y tercera son cláusulas de Horn, pero su cláusula segunda no lo es. La fórmula es satisfactoria, eligiendo x 1 = FALSO, x 2 = FALSO y x 3 arbitrariamente, ya que (FALSO ∨ ¬FALSO) ∧ (¬FALSO ∨ FALSO ∨ x 3 ) ∧ ¬FALSO se evalúa como (FALSO ∨ VERDADERO) ∧ (VERDADERO ∨ FALSO ∨ x 3 ) ∧ VERDADERO, y a su vez a VERDADERO ∧ VERDADERO ∧ VERDADERO (es decir, a VERDADERO). Por el contrario, la fórmula CNF a ∧ ¬ a , que consta de dos cláusulas de un literal, es insatisfactoria, ya que para a =VERDADERO o a =FALSO se evalúa como VERDADERO ∧ ¬VERDADERO (es decir, FALSO) o FALSO ∧ ¬FALSO (es decir , nuevamente FALSO), respectivamente.
Para algunas versiones del problema SAT, es útil definir la noción de fórmula conjuntiva generalizada en forma normal , a saber. como una conjunción de arbitrariamente muchas cláusulas generalizadas , siendo estas últimas de la forma R ( l 1 ,..., ln ) para alguna función booleana R y literales (ordinarios) l i . Diferentes conjuntos de funciones booleanas permitidas conducen a diferentes versiones del problema. Como ejemplo, R (¬ x , a , b ) es una cláusula generalizada, y R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R ( c , d ,¬ z ) es una cláusula generalizada forma normal conjuntiva. Esta fórmula se utiliza a continuación, siendo R el operador ternario que es VERDADERO justo cuando exactamente uno de sus argumentos lo es.
Utilizando las leyes del álgebra de Boole , cada fórmula lógica proposicional se puede transformar en una forma normal conjuntiva equivalente, que, sin embargo, puede ser exponencialmente más larga. Por ejemplo, transformar la fórmula ( x 1 ∧ y 1 ) ∨ ( x 2 ∧ y 2 ) ∨ ... ∨ ( x n ∧ y n ) en forma normal conjuntiva produce
mientras que el primero es una disyunción de n conjunciones de 2 variables, el segundo consta de 2 n cláusulas de n variables.
Sin embargo, con el uso de la transformación de Tseytin , podemos encontrar una fórmula de forma normal conjuntiva equisatisfactible con longitud lineal en el tamaño de la fórmula lógica proposicional original.
SAT fue el primer problema NP-completo conocido , como lo demostró Stephen Cook en la Universidad de Toronto en 1971 [8] e independientemente por Leonid Levin en la Academia de Ciencias de Rusia en 1973. [9] Hasta ese momento, el concepto de El problema NP-completo ni siquiera existía. La prueba muestra cómo cada problema de decisión en la clase de complejidad NP se puede reducir al problema SAT para fórmulas CNF [nota 1] , a veces llamado CNFSAT . Una propiedad útil de la reducción de Cook es que preserva el número de respuestas aceptables. Por ejemplo, decidir si un gráfico determinado tiene 3 colores es otro problema en NP; Si un gráfico tiene 17 3 colores válidos, la fórmula SAT producida por la reducción de Cook-Levin tendrá 17 asignaciones satisfactorias.
La integridad de NP solo se refiere al tiempo de ejecución de las instancias del peor de los casos. Muchos de los casos que se dan en aplicaciones prácticas se pueden solucionar mucho más rápidamente. Consulte Algoritmos para resolver SAT a continuación.
Al igual que el problema de satisfacibilidad de fórmulas arbitrarias, determinar la satisfacibilidad de una fórmula en forma normal conjuntiva donde cada cláusula se limita a como máximo tres literales también es NP-completo; este problema se llama 3-SAT , 3CNFSAT o 3-satisfacibilidad . Para reducir el problema SAT sin restricciones a 3-SAT, transforme cada cláusula l 1 ∨ ⋯ ∨ l n en una conjunción de n - 2 cláusulas
donde x 2 , ⋯ , x n − 2 son variables nuevas que no ocurren en ningún otro lugar. Aunque las dos fórmulas no son lógicamente equivalentes , son equisatisfacibles . La fórmula resultante de transformar todas las cláusulas es como máximo 3 veces más larga que la original, es decir, el crecimiento en longitud es polinómico. [10]
3-SAT es uno de los 21 problemas NP-completos de Karp y se utiliza como punto de partida para demostrar que otros problemas también son NP-difíciles . [nota 2] Esto se hace mediante la reducción del tiempo polinomial de 3-SAT al otro problema. Un ejemplo de un problema en el que se ha utilizado este método es el problema de la camarilla : dada una fórmula CNF que consta de cláusulas c , el gráfico correspondiente consta de un vértice para cada literal y un borde entre cada dos literales no contradictorios [nota 3]. de diferentes cláusulas, cf. imagen. La gráfica tiene una c -clique si y sólo si la fórmula es satisfactoria. [11]
Existe un algoritmo aleatorio simple debido a Schöning (1999) que se ejecuta en el tiempo (4/3) n , donde n es el número de variables en la proposición 3-SAT, y logra con alta probabilidad decidir correctamente 3-SAT. [12]
La hipótesis del tiempo exponencial afirma que ningún algoritmo puede resolver 3-SAT (o incluso k -SAT para cualquier ) en tiempo exp( o ( n )) (es decir, fundamentalmente más rápido que el exponencial en n ).
Selman, Mitchell y Levesque (1996) brindan datos empíricos sobre la dificultad de las fórmulas 3-SAT generadas aleatoriamente, dependiendo de sus parámetros de tamaño. La dificultad se mide en el número de llamadas recursivas realizadas mediante un algoritmo DPLL . Identificaron una región de transición de fase desde fórmulas casi con certeza satisfactorias a fórmulas casi con certeza insatisfactorias en una relación cláusulas-variables de aproximadamente 4,26. [13]
La 3-satisfacibilidad se puede generalizar a k-satisfacibilidad ( k-SAT , también k-CNF-SAT ), cuando se consideran fórmulas en CNF con cada cláusula que contiene hasta k literales. [ cita necesaria ] Sin embargo, dado que para cualquier k ≥ 3, este problema no puede ser más fácil que 3-SAT ni más difícil que SAT, y los dos últimos son NP-completos, por lo que debe ser k-SAT.
Algunos autores restringen k-SAT a fórmulas CNF con exactamente k literales . [ cita necesaria ] Esto tampoco conduce a una clase de complejidad diferente, ya que cada cláusula l 1 ∨ ⋯ ∨ l j con j < k literales se puede completar con variables ficticias fijas para l 1 ∨ ⋯ ∨ l j ∨ d j + 1 ∨ ⋯ ∨ re k . Después de rellenar todas las cláusulas, se deben agregar 2 k -1 cláusulas adicionales [nota 4] para garantizar que solo d 1 = ⋯ = d k =FALSE pueda conducir a una asignación satisfactoria. Dado que k no depende de la longitud de la fórmula, las cláusulas adicionales conducen a un aumento constante de la longitud. Por la misma razón, no importa si se permiten literales duplicados en las cláusulas, como en ¬ x ∨ ¬ y ∨ ¬ y .
La forma normal conjuntiva (en particular con 3 literales por cláusula) a menudo se considera la representación canónica de las fórmulas SAT. Como se muestra arriba, el problema general del SAT se reduce al 3-SAT, el problema de determinar la satisfacibilidad de fórmulas en esta forma.
SAT es trivial si las fórmulas se restringen a aquellas en forma normal disyuntiva , es decir, son una disyunción de conjunciones de literales. De hecho, tal fórmula es satisfactoria si y solo si al menos una de sus conjunciones es satisfactoria, y una conjunción es satisfactoria si y solo si no contiene tanto x como NO x para alguna variable x . Esto se puede comprobar en tiempo lineal. Además, si se restringen a estar en forma normal disyuntiva completa , en la que cada variable aparece exactamente una vez en cada conjunción, se pueden verificar en tiempo constante (cada conjunción representa una asignación satisfactoria). Pero puede llevar tiempo y espacio exponenciales convertir un problema general del SAT a su forma normal disyuntiva; por ejemplo, intercambie "∧" y "∨" en el ejemplo de ampliación exponencial anterior por formas normales conjuntivas.

Una variante del problema de satisfacibilidad 3 es el 3-SAT uno en tres (también conocido como 1-en-3-SAT y exactamente-1 3-SAT ). Dada una forma normal conjuntiva con tres literales por cláusula, el problema es determinar si existe una asignación de verdad a las variables de modo que cada cláusula tenga exactamente un literal VERDADERO (y por lo tanto exactamente dos literales FALDOS). Por el contrario, el 3-SAT ordinario requiere que cada cláusula tenga al menos un literal VERDADERO. Formalmente, un problema 3-SAT uno entre tres se presenta como una forma normal conjuntiva generalizada con todas las cláusulas generalizadas utilizando un operador ternario R que es VERDADERO sólo si exactamente uno de sus argumentos lo es. Cuando todos los literales de una fórmula 3-SAT uno entre tres son positivos, el problema de satisfacibilidad se denomina 3-SAT positivo uno entre tres .
Uno de cada tres 3-SAT, junto con su caso positivo, figura como problema NP-completo "LO4" en la referencia estándar, Computers and Intractability: A Guide to the Theory of NP-Completeness de Michael R. Garey y David. S. Johnson . Thomas Jerome Schaefer demostró que uno de cada tres 3-SAT es NP-completo como un caso especial del teorema de dicotomía de Schaefer , que afirma que cualquier problema que generalice la satisfacibilidad booleana de cierta manera está en la clase P o es NP- completo. [14]
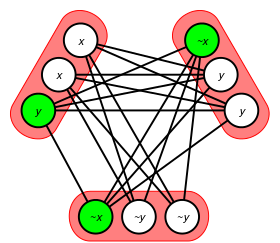
Schaefer ofrece una construcción que permite una fácil reducción del tiempo polinomial de 3-SAT a 3-SAT uno en tres. Sea "( x o y o z )" una cláusula en una fórmula 3CNF. Agregue seis variables booleanas nuevas a , b , c , d , e y f , que se utilizarán para simular esta cláusula y ninguna otra. Entonces la fórmula R ( x , a , d ) ∧ R ( y , b , d ) ∧ R ( a , b , e ) ∧ R ( c , d , f ) ∧ R ( z , c ,FALSE) es satisfactoria por alguna configuración de las variables nuevas si y solo si al menos uno de x , y o z es VERDADERO, vea la imagen (izquierda). Por lo tanto, cualquier instancia de 3-SAT con m cláusulas yn variables puede convertirse en una instancia de 3-SAT equisatisfactible una entre tres con 5 m cláusulas yn +6 m variables. [15] Otra reducción involucra solo cuatro variables nuevas y tres cláusulas: R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R( c , d ,¬ z ), ver imagen (derecha).
Otra variante es el problema de 3 satisfacibilidad no todos iguales (también llamado NAE3SAT ). Dada una forma normal conjuntiva con tres literales por cláusula, el problema es determinar si existe una asignación a las variables tal que en ninguna cláusula los tres literales tengan el mismo valor de verdad. Este problema también es NP-completo, incluso si no se admiten símbolos de negación, según el teorema de dicotomía de Schaefer. [14]
Una fórmula 3-SAT es SAT lineal ( LSAT ) si cada cláusula (vista como un conjunto de literales) se cruza como máximo con otra cláusula y, además, si dos cláusulas se cruzan, entonces tienen exactamente un literal en común. Una fórmula LSAT se puede representar como un conjunto de intervalos semicerrados disjuntos en una línea. Decidir si una fórmula LSAT es satisfactoria es NP-completo. [dieciséis]
SAT es más fácil si el número de literales en una cláusula se limita a 2 como máximo, en cuyo caso el problema se llama 2-SAT . Este problema se puede resolver en tiempo polinomial y, de hecho, está completo para la clase de complejidad NL . Si además todas las operaciones OR en literales se cambian a operaciones XOR , el resultado se llama satisfacibilidad exclusiva o 2 , lo cual es un problema completo para la clase de complejidad SL = L.
El problema de decidir la satisfacibilidad de una conjunción dada de cláusulas de Horn se llama satisfacibilidad de Horn o HORN-SAT . Se puede resolver en tiempo polinomial mediante un solo paso del algoritmo de propagación unitaria , que produce el modelo mínimo único del conjunto de cláusulas Horn (con el conjunto de literales asignados a VERDADERO). La satisfacibilidad de Horn es P-completa . Puede verse como la versión de P del problema booleano de satisfacibilidad. Además, decidir la verdad de las fórmulas de Horn cuantificadas se puede hacer en tiempo polinomial.[17]
Las cláusulas de cuerno son interesantes porque pueden expresar la implicación de una variable a partir de un conjunto de otras variables. De hecho, una de esas cláusulas ¬ x 1 ∨ ... ∨ ¬ x n ∨ y se puede reescribir como x 1 ∧ ... ∧ x n → y , es decir, si x 1 ,..., x n son todas VERDADERAS , entonces y también debe ser VERDADERO.
Una generalización de la clase de fórmulas de Horn es la de fórmulas de Horn renombrables, que es el conjunto de fórmulas que se pueden colocar en forma de Horn reemplazando algunas variables con su respectiva negación. Por ejemplo, ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 no es una fórmula de Horn, pero se le puede cambiar el nombre a fórmula de Horn ( x 1 ∨ ¬ x 2 ) ∧ (¬ x 1 ∨ x 2 ∨ ¬ y 3 ) ∧ ¬ x 1 introduciendo y 3 como negación de x 3 . Por el contrario, ningún cambio de nombre de ( x 1 ∨ ¬ x 2 ∨ ¬ x 3 ) ∧ (¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 1 conduce a una fórmula de Horn. La comprobación de la existencia de dicho reemplazo se puede realizar en tiempo lineal; por lo tanto, la satisfacibilidad de dichas fórmulas está en P, ya que se puede resolver realizando primero este reemplazo y luego verificando la satisfacibilidad de la fórmula de Horn resultante.
Otro caso especial es la clase de problemas en los que cada cláusula contiene operadores XOR (es decir, exclusivos o ) en lugar de operadores OR (simples). [nota 5] Esto está en P , ya que una fórmula XOR-SAT también puede verse como un sistema de ecuaciones lineales mod 2, y puede resolverse en tiempo cúbico mediante eliminación gaussiana ; [18] consulte el cuadro para ver un ejemplo. Esta refundición se basa en el parentesco entre las álgebras booleanas y los anillos booleanos , y en el hecho de que la aritmética módulo dos forma un campo finito . Dado que a XOR b XOR c se evalúa como VERDADERO si y solo si exactamente 1 o 3 miembros de { a , b , c } son VERDADEROS, cada solución del problema 1-en-3-SAT para una fórmula CNF dada también es una solución del problema XOR-3-SAT, y a su vez cada solución de XOR-3-SAT es una solución de 3-SAT, cf. imagen. Como consecuencia, para cada fórmula CNF, es posible resolver el problema XOR-3-SAT definido por la fórmula y, basándose en el resultado, inferir que el problema 3-SAT tiene solución o que el problema 1-en-3- El problema del SAT no tiene solución.
Siempre que las clases de complejidad P y NP no sean iguales , ni la satisfacibilidad 2, ni Horn, ni XOR son NP completas, a diferencia de SAT.
Las restricciones anteriores (CNF, 2CNF, 3CNF, Horn, XOR-SAT) vinculaban las fórmulas consideradas a ser conjunciones de subfórmulas; cada restricción establece una forma específica para todas las subfórmulas: por ejemplo, sólo las cláusulas binarias pueden ser subfórmulas en 2CNF.
El teorema de dicotomía de Schaefer establece que, para cualquier restricción a funciones booleanas que puedan usarse para formar estas subfórmulas, el problema de satisfacibilidad correspondiente está en P o NP-completo. La pertenencia a P de la satisfacibilidad de las fórmulas 2CNF, Horn y XOR-SAT son casos especiales de este teorema. [14]
La siguiente tabla resume algunas variantes comunes del SAT.
Una extensión que ha ganado una popularidad significativa desde 2003 son las teorías del módulo de satisfacibilidad ( SMT ) que pueden enriquecer las fórmulas CNF con restricciones lineales, matrices, restricciones completamente diferentes, funciones no interpretadas , [19] , etc. Estas extensiones suelen seguir siendo NP-completas, pero muy Ahora hay disponibles solucionadores eficientes que pueden manejar muchos tipos de restricciones de este tipo.
El problema de la satisfacibilidad se vuelve más difícil si se permite que los cuantificadores "para todos" ( ∀ ) y "existe" ( ∃ ) vinculen las variables booleanas. Un ejemplo de tal expresión sería ∀ x ∀ y ∃ z ( x ∨ y ∨ z ) ∧ (¬ x ∨ ¬ y ∨ ¬ z ) ; es válido, ya que para todos los valores de x e y , se puede encontrar un valor apropiado de z , a saber. z = VERDADERO si tanto x como y son FALSO, y z = FALSO en caso contrario. El propio SAT (tácitamente) utiliza sólo cuantificadores ∃. Si en su lugar solo se permiten cuantificadores ∀, se obtiene el llamado problema de tautología , que es co-NP-completo . Si se permiten ambos cuantificadores, el problema se denomina problema de fórmula booleana cuantificada ( QBF ), que se puede demostrar que es PSPACE completo . Se cree ampliamente que los problemas de PSPACE completo son estrictamente más difíciles que cualquier problema de NP, aunque esto aún no se ha demostrado. Utilizando sistemas P altamente paralelos , los problemas QBF-SAT se pueden resolver en tiempo lineal. [20]
El SAT ordinario pregunta si hay al menos una asignación de variable que haga que la fórmula sea verdadera. Existen diversas variantes que se ocupan del número de dichas asignaciones:
Otras generalizaciones incluyen la satisfacibilidad para la lógica de primer y segundo orden , problemas de satisfacción de restricciones y programación entera 0-1 .
Si bien el SAT es un problema de decisión , el problema de búsqueda para encontrar una tarea satisfactoria se reduce al SAT. Es decir, cada algoritmo que responda correctamente si una instancia de SAT tiene solución se puede utilizar para encontrar una tarea satisfactoria. Primero, se hace la pregunta sobre la fórmula dada Φ. Si la respuesta es "no", la fórmula es insatisfactoria. De lo contrario, la pregunta se formula sobre la fórmula parcialmente instanciada Φ { x 1 =TRUE} , es decir Φ con la primera variable x 1 reemplazada por TRUE y simplificada en consecuencia. Si la respuesta es "sí", entonces x 1 = VERDADERO, en caso contrario x 1 = FALSO. Los valores de otras variables se pueden encontrar posteriormente de la misma manera. En total, se requieren n +1 ejecuciones del algoritmo, donde n es el número de variables distintas en Φ.
Esta propiedad se utiliza en varios teoremas de la teoría de la complejidad:
Dado que el problema SAT es NP-completo, solo se conocen algoritmos con complejidad exponencial en el peor de los casos. A pesar de esto, durante la década de 2000 se desarrollaron algoritmos eficientes y escalables para SAT que han contribuido a avances dramáticos en nuestra capacidad para resolver automáticamente instancias de problemas que involucran decenas de miles de variables y millones de restricciones (es decir, cláusulas). [1] Ejemplos de tales problemas en la automatización del diseño electrónico (EDA) incluyen verificación de equivalencia formal , verificación de modelos , verificación formal de microprocesadores canalizados , [19] generación automática de patrones de prueba , enrutamiento de FPGA , [26] problemas de planificación y programación , y pronto. Un motor de resolución SAT también se considera un componente esencial en la caja de herramientas de automatización del diseño electrónico .
Las principales técnicas utilizadas por los solucionadores SAT modernos incluyen el algoritmo Davis-Putnam-Logemann-Loveland (o DPLL), el aprendizaje de cláusulas basado en conflictos (CDCL) y algoritmos de búsqueda local estocástica como WalkSAT . Casi todos los solucionadores del SAT incluyen tiempos de espera, por lo que finalizarán en un tiempo razonable incluso si no pueden encontrar una solución. Diferentes solucionadores del SAT encontrarán diferentes casos fáciles o difíciles, y algunos se destacan en demostrar la insatisfacción y otros en encontrar soluciones. Se han realizado intentos recientes para aprender la satisfacibilidad de una instancia utilizando técnicas de aprendizaje profundo. [27]
Los solucionadores de SAT se desarrollan y comparan en concursos de resolución de SAT. [28] Los solucionadores SAT modernos también están teniendo un impacto significativo en los campos de la verificación de software, la resolución de restricciones en inteligencia artificial y la investigación de operaciones, entre otros.
los solucionadores SAT modernos a menudo pueden manejar problemas con millones de restricciones y cientos de miles de variables..
(por fecha de publicación)