Magnetoquímica

Estudio de las propiedades magnéticas de los compuestos químicos.

La magnetoquímica se ocupa de las propiedades magnéticas de los compuestos químicos . Las propiedades magnéticas surgen del espín y el momento angular orbital de los electrones contenidos en un compuesto. Los compuestos son diamagnéticos cuando no contienen electrones desapareados . Los compuestos moleculares que contienen uno o más electrones desapareados son paramagnéticos . La magnitud del paramagnetismo se expresa como un momento magnético efectivo, μ _{eff . Para} los metales de transición de primera fila, la magnitud de μ _eff es, en una primera aproximación, una función simple del número de electrones desapareados, la fórmula de solo espín. En general, el acoplamiento espín-órbita hace que μ _eff se desvíe de la fórmula de solo espín. Para los metales de transición más pesados, los lantánidos y los actínidos , el acoplamiento espín-órbita no se puede ignorar. La interacción de intercambio puede ocurrir en grupos y redes infinitas, lo que resulta en ferromagnetismo , antiferromagnetismo o ferrimagnetismo dependiendo de las orientaciones relativas de los espines individuales.

Susceptibilidad magnética

La principal medida en magnetoquímica es la susceptibilidad magnética. Esta mide la fuerza de interacción al colocar la sustancia en un campo magnético. La susceptibilidad magnética volumétrica , representada por el símbolo, se define por la relación ${\displaystyle \chi _{v}}$

${\displaystyle {\vec {M}}=\chi _{v}{\vec {H}}}$

donde, es la magnetización del material (el momento dipolar magnético por unidad de volumen), medida en amperios por metro ( unidades del SI ), y es la intensidad del campo magnético , también medida en amperios por metro. La susceptibilidad es una cantidad adimensional . Para aplicaciones químicas, la susceptibilidad magnética molar (χ _mol ) es la cantidad preferida. Se mide en m ³ ·mol ⁻¹ (SI) o cm ³ ·mol ⁻¹ (CGS) y se define como ${\displaystyle {\vec {M}}}$ ${\displaystyle {\vec {H}}}$

${\displaystyle \chi _{\text{mol}}=M\chi _{v}/\rho }$

donde ρ es la densidad en kg·m ⁻³ (SI) o g·cm ⁻³ (CGS) y M es la masa molar en kg·mol ⁻¹ (SI) o g·mol ⁻¹ (CGS).

Diagrama esquemático de la balanza de Gouy

Existen diversos métodos disponibles para medir la susceptibilidad magnética.

• Con la balanza Gouy, el cambio de peso de la muestra se mide con una balanza analítica cuando la muestra se coloca en un campo magnético homogéneo. Las mediciones se calibran con un estándar conocido, como el tiocianato de cobalto y mercurio, HgCo(NCS) ₄ . La calibración elimina la necesidad de conocer la densidad de la muestra. Se pueden realizar mediciones de temperatura variable colocando la muestra en un criostato entre las piezas polares del imán. ^[1]
• La balanza de Evans ^[2] es una balanza de torsión que utiliza una muestra en una posición fija y un imán secundario variable para devolver los imanes a su posición inicial. También está calibrada frente a HgCo(NCS) ₄ .
• Con una balanza de Faraday, la muestra se coloca en un campo magnético de gradiente constante y se pesa en una balanza de torsión. Este método puede brindar información sobre la anisotropía magnética . ^[3]
• SQUID es un magnetómetro muy sensible.
• Para las sustancias en solución, se puede utilizar la RMN para medir la susceptibilidad. ^{[4] [5]}

Tipos de comportamiento magnético

Cuando un átomo aislado se coloca en un campo magnético se produce una interacción porque cada electrón del átomo se comporta como un imán, es decir, el electrón tiene un momento magnético . Existen dos tipos de interacción.

1. Diamagnetismo. Cuando se coloca el átomo en un campo magnético, se polariza magnéticamente, es decir, desarrolla un momento magnético inducido. La fuerza de la interacción tiende a empujar al átomo fuera del campo magnético. Por convención, la susceptibilidad diamagnética se le da un signo negativo. Muy frecuentemente, los átomos diamagnéticos no tienen electrones desapareados, es decir, cada electrón está apareado con otro electrón en el mismo orbital atómico . Los momentos de los dos electrones se cancelan entre sí, por lo que el átomo no tiene momento magnético neto. Sin embargo, para el ion Eu ³⁺ que tiene seis electrones desapareados, el momento angular orbital cancela el momento angular del electrón, y este ion es diamagnético a cero Kelvin.
2. Paramagnetismo. Al menos un electrón no está apareado con otro. El átomo tiene un momento magnético permanente. Cuando se coloca en un campo magnético, el átomo es atraído hacia el campo. Por convención, la susceptibilidad paramagnética se le asigna un signo positivo.

Cuando el átomo está presente en un compuesto químico, su comportamiento magnético se ve modificado por su entorno químico. La medición del momento magnético puede proporcionar información química útil.

En ciertos materiales cristalinos, los momentos magnéticos individuales pueden estar alineados entre sí (el momento magnético tiene magnitud y dirección). Esto da lugar al ferromagnetismo , antiferromagnetismo o ferrimagnetismo . Se trata de propiedades del cristal en su conjunto, que tienen poca relación con las propiedades químicas.

Diamagnetismo

El diamagnetismo es una propiedad universal de los compuestos químicos, ya que todos ellos contienen pares de electrones. Un compuesto en el que no hay electrones desapareados se dice que es diamagnético. El efecto es débil porque depende de la magnitud del momento magnético inducido, es decir, del número de pares de electrones y de la naturaleza química de los átomos a los que pertenecen. Esto significa que los efectos son aditivos y se puede elaborar una tabla de "contribuciones diamagnéticas", o constantes de Pascal . ^{[6] [7] [8]} En el caso de los compuestos paramagnéticos, la susceptibilidad observada se puede ajustar añadiéndole la llamada corrección diamagnética, que es la susceptibilidad diamagnética calculada con los valores de la tabla. ^[9]

Paramagnetismo

Mecanismo y dependencia de la temperatura

Variación de la susceptibilidad magnética con la temperatura

Un ion metálico con un solo electrón desapareado, como Cu ²⁺ , en un complejo de coordinación proporciona la ilustración más simple del mecanismo del paramagnetismo. Los iones metálicos individuales se mantienen alejados entre sí por los ligandos, de modo que no hay interacción magnética entre ellos. Se dice que el sistema está magnéticamente diluido. Los dipolos magnéticos de los átomos apuntan en direcciones aleatorias. Cuando se aplica un campo magnético, se produce la división Zeeman de primer orden . Los átomos con espines alineados con el campo superan ligeramente en número a los átomos con espines no alineados. En el efecto Zeeman de primer orden, la diferencia de energía entre los dos estados es proporcional a la intensidad del campo aplicado. Denotando la diferencia de energía como Δ E , la distribución de Boltzmann da la relación de las dos poblaciones como , donde k es la constante de Boltzmann y T es la temperatura en kelvin . En la mayoría de los casos Δ E es mucho menor que kT y la exponencial se puede expandir como 1 – Δ E/kT . De la presencia de 1/ T en esta expresión se deduce que la susceptibilidad es inversamente proporcional a la temperatura. ^[10] ${\displaystyle e^{-\Delta E/kT}}$

${\displaystyle \chi ={C \over T}}$

Esto se conoce como la ley de Curie y la constante de proporcionalidad, C , se conoce como la constante de Curie , cuyo valor, para la susceptibilidad molar, se calcula como ^[11]

${\displaystyle C={\frac {Ng^{2}S(S+1)\mu _{B}^{2}}{3k}}}$

donde N es la constante de Avogadro , g es el factor g de Landé y μ _B es el magnetón de Bohr . En este tratamiento se ha asumido que el estado fundamental electrónico no está degenerado, que la susceptibilidad magnética se debe únicamente al espín del electrón y que únicamente el estado fundamental está poblado térmicamente.

Mientras que algunas sustancias obedecen la ley de Curie, otras obedecen la ley de Curie-Weiss .

${\displaystyle \chi ={\frac {C}{T-T_{c}}}}$

T _c es la temperatura de Curie . La ley de Curie-Weiss se aplicará únicamente cuando la temperatura sea muy superior a la temperatura de Curie. A temperaturas inferiores a la temperatura de Curie, la sustancia puede volverse ferromagnética . Se observa un comportamiento más complicado con los elementos de transición más pesados.

Momento magnético efectivo

Cuando se cumple la ley de Curie, el producto de la susceptibilidad molar por la temperatura es una constante. El momento magnético efectivo , μ _eff , se define entonces ^[12] como

${\displaystyle \mu _{\text{eff}}=\mathrm {constant} {\sqrt {T\chi }}}$

Donde C tiene unidades CGS cm3 ^mol −1 ^K , μ _eff es

${\displaystyle \mu _{\text{eff}}={\sqrt {3k \over N\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 2.82787{\sqrt {T\chi }}}$

Donde C tiene unidades SI m ³ mol ⁻¹ K, μ _eff es

${\displaystyle \mu _{\text{eff}}={\sqrt {3k \over N\mu _{0}\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 797.727{\sqrt {T\chi }}}$

La cantidad μ _eff es efectivamente adimensional, pero a menudo se expresa en unidades de magnetón de Bohr (μ _B ). ^[12]

En el caso de las sustancias que obedecen a la ley de Curie, el momento magnético efectivo es independiente de la temperatura. En el caso de otras sustancias, μ _eff depende de la temperatura, pero la dependencia es pequeña si se cumple la ley de Curie-Weiss y la temperatura de Curie es baja.

Paramagnetismo independiente de la temperatura

Los compuestos que se espera que sean diamagnéticos pueden exhibir este tipo de paramagnetismo débil. Surge de un efecto Zeeman de segundo orden en el que se produce una división adicional, proporcional al cuadrado de la intensidad del campo. Es difícil de observar ya que el compuesto inevitablemente también interactúa con el campo magnético en el sentido diamagnético. Sin embargo, hay datos disponibles para el ion permanganato . ^[13] Es más fácil de observar en compuestos de elementos más pesados, como los compuestos de uranilo .

Interacciones de intercambio

Acetato de cobre (II) dihidrato ^[14]

Ordenamiento ferrimagnético en 2 dimensiones

Ordenamiento antiferromagnético en 2 dimensiones

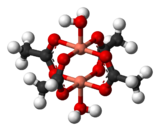
Las interacciones de intercambio ocurren cuando la sustancia no está magnéticamente diluida y hay interacciones entre centros magnéticos individuales. Uno de los sistemas más simples para exhibir el resultado de las interacciones de intercambio es el acetato de cobre (II) cristalino , Cu ₂ (OAc) ₄ (H ₂ O) ₂ . Como indica la fórmula, contiene dos iones de cobre (II). Los iones Cu ²⁺ se mantienen unidos por cuatro ligandos de acetato, cada uno de los cuales se une a ambos iones de cobre. Cada ion Cu ²⁺ tiene una configuración electrónica ad ⁹ , y por lo tanto debería tener un electrón desapareado. Si hubiera un enlace covalente entre los iones de cobre, los electrones se aparearían y el compuesto sería diamagnético. En cambio, hay una interacción de intercambio en la que los espines de los electrones desapareados se alinean parcialmente entre sí. De hecho, se crean dos estados, uno con espines paralelos y el otro con espines opuestos. La diferencia de energía entre los dos estados es tan pequeña que sus poblaciones varían significativamente con la temperatura. En consecuencia, el momento magnético varía con la temperatura en un patrón sigmoideo . El estado con espines opuestos tiene menor energía, por lo que la interacción puede clasificarse como antiferromagnética en este caso. ^[14] Se cree que este es un ejemplo de superintercambio , mediado por los átomos de oxígeno y carbono de los ligandos de acetato. ^[15] Otros dímeros y grupos exhiben un comportamiento de intercambio. ^[16]

Las interacciones de intercambio pueden actuar sobre cadenas infinitas en una dimensión, sobre planos en dos dimensiones o sobre un cristal entero en tres dimensiones. Estos son ejemplos de ordenamiento magnético de largo alcance. Dan lugar al ferromagnetismo , al antiferromagnetismo o al ferrimagnetismo , dependiendo de la naturaleza y las orientaciones relativas de los espines individuales. ^[17]

Los compuestos a temperaturas inferiores a la temperatura de Curie exhiben un orden magnético de largo alcance en forma de ferromagnetismo. Otra temperatura crítica es la temperatura de Néel , por debajo de la cual se produce el antiferromagnetismo. El hexahidrato de cloruro de níquel, NiCl ₂ ·6H ₂ O, tiene una temperatura de Néel de 8,3 K. La susceptibilidad es máxima a esta temperatura. Por debajo de la temperatura de Néel, la susceptibilidad disminuye y la sustancia se vuelve antiferromagnética. ^[18]

Complejos de iones de metales de transición

El momento magnético efectivo para un compuesto que contiene un ion de metal de transición con uno o más electrones desapareados depende del momento angular de espín y orbital total de los electrones desapareados, y , respectivamente. "Total" en este contexto significa " suma vectorial ". En la aproximación de que los estados electrónicos de los iones metálicos están determinados por el acoplamiento de Russell-Saunders y que el acoplamiento espín-órbita es despreciable, el momento magnético viene dado por ^[19] ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {S}}}$

${\displaystyle \mu _{\text{eff}}={\sqrt {{\vec {L}}({\vec {L}}+1)+4{\vec {S}}({\vec {S}}+1)}}\mu _{B}}$

Fórmula de solo centrifugado

El momento angular orbital se genera cuando un electrón en un orbital de un conjunto degenerado de orbitales se mueve a otro orbital del conjunto por rotación. En complejos de baja simetría, ciertas rotaciones no son posibles. En ese caso, se dice que el momento angular orbital está "extinguido" y es menor de lo que podría esperarse (extinción parcial) o cero (extinción completa). Existe extinción completa en los siguientes casos. Nótese que un electrón en un par degenerado de orbitales d _{x ² –y ²} o d _{z ²} no puede rotar hacia el otro orbital debido a la simetría. ^[20] ${\displaystyle {\vec {L}}}$

leyenda: t _2g , t ₂ = (d _xy , d _xz , d _yz ). e _g , e = (d _{x ² –y ²} , d _{z ²} ).

Cuando el momento angular orbital se extingue por completo, el paramagnetismo se puede atribuir únicamente al espín del electrón. El momento angular de espín total es simplemente la mitad del número de electrones desapareados y resulta la fórmula de solo espín. ${\displaystyle {\vec {L}}=0}$

${\displaystyle \mu _{\text{eff}}={\sqrt {n(n+2)}}\mu _{B}}$

donde n es el número de electrones desapareados. La fórmula de solo espín es una buena primera aproximación para complejos de alto espín de metales de transición de primera fila . ^[21]

Las pequeñas desviaciones de la fórmula de solo espín pueden ser resultado de no tener en cuenta el momento angular orbital o el acoplamiento espín-órbita. Por ejemplo, los complejos tetraédricos d ³ , d ⁴ , d ⁸ y d ⁹ tienden a mostrar mayores desviaciones de la fórmula de solo espín que los complejos octaédricos del mismo ion, porque la "extinción" de la contribución orbital es menos efectiva en el caso tetraédrico. ^[22]

Complejos de bajo espín

Diagrama del campo cristalino para el octaedro de bajo espín d ⁵

Diagrama del campo cristalino para el octaedro de alto espín d ⁵

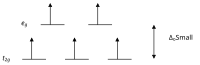
Según la teoría de campos cristalinos, los orbitales d de un ion metálico de transición en un complejo octaédrico se dividen en dos grupos en un campo cristalino. Si la división es lo suficientemente grande como para superar la energía necesaria para colocar electrones en el mismo orbital, con espín opuesto, se obtendrá un complejo de espín bajo.

Con un electrón desapareado, los valores _{de μeff} varían de 1,8 a 2,5 _μB y con dos electrones desapareados, el rango es de 3,18 a 3,3 _μB . Nótese que los complejos de bajo espín de Fe ²⁺ y Co ³⁺ son diamagnéticos. Otro grupo de complejos que son diamagnéticos son los complejos cuadrado-planares de iones d ⁸ como Ni ²⁺ y Rh ⁺ y Au ³⁺ .

Cruce de giros

Cuando la diferencia de energía entre los estados de alto y bajo espín es comparable a kT ( k es la constante de Boltzmann y T la temperatura), se establece un equilibrio entre los estados de espín, que involucra lo que se ha llamado "isómeros electrónicos". El tris- ditiocarbamato de hierro(III), Fe(S ₂ CNR ₂ ) ₃ , es un ejemplo bien documentado. El momento efectivo varía desde un valor típico de d ⁵ de espín bajo de 2,25 μ _B a 80 K hasta más de 4 μ _B por encima de 300 K. ^[23]

Metales de transición de 2.ª y 3.ª fila

La división del campo cristalino es mayor para los complejos de metales de transición más pesados ​​que para los metales de transición analizados anteriormente. Una consecuencia de esto es que los complejos de bajo espín son mucho más comunes. Las constantes de acoplamiento espín-órbita, ζ, también son mayores y no se pueden ignorar, incluso en tratamientos elementales. El comportamiento magnético se ha resumido, como se muestra a continuación, junto con una extensa tabla de datos. ^[24]

Lantánidos y actínidos

El acoplamiento Russell-Saunders , acoplamiento LS, se aplica a los iones lantánidos; los efectos del campo cristalino se pueden ignorar, pero el acoplamiento espín-órbita no es despreciable. En consecuencia, los momentos angulares de espín y orbitales deben combinarse

${\displaystyle {\vec {L}}=\sum _{i}{\vec {l}}_{i}}$

${\displaystyle {\vec {S}}=\sum _{i}{\vec {s}}_{i}}$

${\displaystyle {\vec {J}}={\vec {L}}+{\vec {S}}}$

y el momento magnético calculado viene dado por

${\displaystyle \mu _{\text{eff}}=g{\sqrt {{\vec {J}}({\vec {J}}+1)}};g={3 \over 2}+{\frac {{\vec {S}}({\vec {S}}+1)-{\vec {L}}({\vec {L}}+1)}{2{\vec {J}}({\vec {J}}+1)}}}$

En los actínidos, el acoplamiento espín-órbita es fuerte y el acoplamiento se aproxima al acoplamiento j j .

${\displaystyle {\vec {J}}=\sum _{i}{\vec {j}}_{i}=\sum _{i}({\vec {l}}_{i}+{\vec {s}}_{i})}$

Esto significa que es difícil calcular el momento efectivo. Por ejemplo, el uranio(IV), f ² , en el complejo [UCl ₆ ] ²⁻ tiene un momento efectivo medido de 2,2 μ _B , que incluye una contribución del paramagnetismo independiente de la temperatura. ^[26]

Elementos del grupo principal y compuestos orgánicos

Espectro EPR simulado del radical CH _{3 •}

Etiqueta de giro MSTL

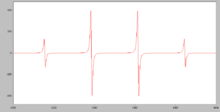
Muy pocos compuestos de elementos del grupo principal son paramagnéticos. Ejemplos notables incluyen: oxígeno , O ₂ ; óxido nítrico , NO; dióxido de nitrógeno , NO ₂ y dióxido de cloro , ClO ₂ . En química orgánica , los compuestos con un electrón desapareado se dice que son radicales libres . Los radicales libres, con algunas excepciones, tienen una vida corta porque un radical libre reaccionará rápidamente con otro, por lo que sus propiedades magnéticas son difíciles de estudiar. Sin embargo, si los radicales están bien separados entre sí en una solución diluida en una matriz sólida, a baja temperatura, pueden estudiarse por resonancia paramagnética electrónica (EPR). Dichos radicales se generan por irradiación. Amplios estudios de EPR han revelado mucho sobre la deslocalización de electrones en radicales libres. El espectro simulado del radical CH ₃ • muestra una división hiperfina debido a la interacción del electrón con los 3 núcleos de hidrógeno equivalentes, cada uno de los cuales tiene un espín de 1/2. ^{[27] [28]}

Los marcadores de espín son radicales libres de larga duración que se pueden insertar en moléculas orgánicas para que puedan estudiarse mediante EPR. ^[29] Por ejemplo, el nitróxido MTSL , un derivado funcionalizado del óxido de tetrametilpiperidina, TEMPO , se utiliza en el marcado de espín dirigido al sitio .

Aplicaciones

El ion de gadolinio , Gd ³⁺ , tiene la configuración electrónica f ⁷ , con todos los espines paralelos. Los compuestos del ion Gd ^{3+ son los más adecuados para su uso como} agente de contraste para exploraciones de resonancia magnética . ^[30] Los momentos magnéticos de los compuestos de gadolinio son mayores que los de cualquier ion de metal de transición. El gadolinio se prefiere a otros iones de lantánidos, algunos de los cuales tienen momentos efectivos mayores, debido a que tiene un estado fundamental electrónico no degenerado . ^[31]

Durante muchos años, la naturaleza de la oxihemoglobina , Hb-O ₂ , fue muy controvertida. Experimentalmente se descubrió que era diamagnética. Se acepta generalmente que la desoxihemoglobina es un complejo de hierro en el estado de oxidación +2 , es decir, un sistema ad ⁶ con un momento magnético de espín alto cercano al valor de solo espín de 4,9 μ _B . Se propuso que el hierro se oxida y el oxígeno se reduce a superóxido.

Fe(II)Hb (alto espín) + O ₂ ⇌ [Fe(III)Hb]O ₂ ⁻

Se propuso entonces que el apareamiento de electrones de Fe ³⁺ y O ₂ ⁻ se producía mediante un mecanismo de intercambio. Ahora se ha demostrado que, de hecho, el hierro(II) cambia de espín alto a espín bajo cuando una molécula de oxígeno dona un par de electrones al hierro. Mientras que en la desoxihemoglobina el átomo de hierro se encuentra por encima del plano del hemo, en el complejo de espín bajo el radio iónico efectivo se reduce y el átomo de hierro se encuentra en el plano del hemo. ^[32]

Fe(II)Hb + O ₂ ⇌ [Fe(II)Hb]O ₂ (espín bajo)

Esta información tiene una importancia importante en la investigación para encontrar transportadores artificiales de oxígeno .

Los compuestos de galio(II) eran desconocidos hasta hace muy poco. Como el número atómico del galio es un número impar (31), Ga ²⁺ debería tener un electrón desapareado. Se suponía que actuaría como un radical libre y tendría una vida útil muy corta. La inexistencia de compuestos de Ga(II) era parte del llamado efecto de par inerte . Cuando se sintetizaron sales del anión con fórmula empírica como [GaCl ₃ ] ⁻ se descubrió que eran diamagnéticas. Esto implicaba la formación de un enlace Ga-Ga y una fórmula dimérica, [Ga ₂ Cl ₆ ] ²⁻ . ^[33]

Véase también

• Mineralogía magnética
• Magnetoelectroquímica
• Líquido iónico magnético
• Hielo giratorio
• Vidrio giratorio
• Superdiamagnetismo , Superparamagnetismo , Superferromagnetismo
• Magnetismo de una sola molécula

Referencias

1. Earnshaw, pág. 89
2. Balanzas de susceptibilidad magnética
3. O'Connor, CJ (1982). Lippard, SJ (ed.). Mediciones de susceptibilidad magnética . Progreso en química inorgánica. Vol. 29. Wiley. pág. 203. ISBN. 978-0-470-16680-2.
4. Evans, DF (1959). "La determinación de la susceptibilidad paramagnética de sustancias en solución por resonancia magnética nuclear". J. Chem. Soc. : 2003–2005. doi :10.1039/JR9590002003.
5. Huerto, pág. 15. Earnshshaw, pág. 97
6. Figgis y Lewis, pág. 403
7. Carlin, pág. 3
8. Bain, Gordon A.; Berry, John F. (2008). "Correcciones diamagnéticas y constantes de Pascal". J. Chem. Educ . 85 (4): 532. Bibcode :2008JChEd..85..532B. doi :10.1021/ed085p532.
9. Figgis y Lewis, pág. 417
10. Figgis y Lewis, pág. 419
11. Huerto, pág. 48
12. Hoppe, JI (1972). "Momento magnético efectivo". J. Chem. Educ . 49 (7): 505. Código Bibliográfico : 1972JChEd..49..505H. doi : 10.1021/ed049p505.
13. Huerto, pág. 53
14. Lawrence Que (marzo de 2000). Métodos físicos en química bioinorgánica: espectroscopia y magnetismo. University Science Books. págs. 345–348. ISBN 978-1-891389-02-3. Recuperado el 22 de febrero de 2011 .
15. Figgis y Lewis, pag. 435. Huerto, pág. 67
16. Carlin, secciones 5.5–5.7
17. Carlin, capítulos 6 y 7, págs. 112-225
18. Carin, pág. 264
19. Figgis y Lewis, pág. 420
20. Figgis y Lewis, págs. 424, 432
21. Figgis y Lewis, pág. 406
22. Figgis&Lewis, Sección 3, "Contribución orbital"
23. Huerto, pág. 125. Carlin, pág. 270
24. Figgis y Lewis, págs. 443-451
25. Greenwood y Earnshaw, pág. 1243
26. Huerto, pág. 106
27. Weil, John A.; Bolton, James R.; Wertz, John E. (1994). Resonancia paramagnética electrónica: teoría elemental y aplicaciones prácticas . Wiley. ISBN 0-471-57234-9.
28. Atkins, PW; Symons, MCR (1967). La estructura de los radicales inorgánicos; una aplicación de la resonancia de espín electrónico al estudio de la estructura molecular . Elsevier.
29. Berliner, LJ (1976). Etiquetado de espín: teoría y aplicaciones I. Academic Press. ISBN 0-12-092350-5.Berliner, LJ (1979). Etiquetado de espín II: teoría y aplicaciones . Academic Press. ISBN 0-12-092352-1.
30. Krause, W. (2002). Agentes de contraste I: Imágenes por resonancia magnética: Parte 1. Springer. ISBN 3540422471.
31. Caravan, Peter; Ellison, Jeffrey J.; McMurry, Thomas J.; Lauffer, Randall B., Jeffrey J.; McMurry, Thomas J.; Lauffer, Randall B. (1999). "Quelatos de gadolinio (III) como agentes de contraste para resonancia magnética: estructura, dinámica y aplicaciones". Chem. Rev. 99 ( 9): 2293–2352. doi :10.1021/cr980440x. PMID  11749483.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
32. Greenwood y Earnshaw, págs. 1099-1011
33. Greenwood y Earnshaw, pág. 240

Bibliografía

• Carlin, RL (1986). Magnetoquímica . Springer . ISBN. 978-3-540-15816-5.
• Earnshaw, Alan (1968). Introducción a la magnetoquímica . Academic Press .
• Figgis, BN; Lewis, J. (1960). "La magnetoquímica de compuestos complejos". En Lewis. J. y Wilkins. RG (ed.). Química de coordinación moderna . Nueva York: Wiley .
• Greenwood, Norman N. ; Earnshaw, Alan (1997). Química de los elementos (2.ª ed.). Butterworth-Heinemann . ISBN 978-0-08-037941-8.
• Orchard, AF (2003). Magnetoquímica . Oxford Chemistry Primers. Oxford University Press . ISBN 0-19-879278-6.
• Selwood, PW (1943). Magnetoquímica. Interscience Publishers Inc.
• Vulfson, Sergey (1998). Magnetoquímica molecular . Taylor y Francisco . ISBN 90-5699-535-9.

Enlaces externos

• Recursos de información disponibles en línea sobre magnetoquímica
• Tablas de correcciones diamagnéticas y constantes de Pascal