Emisión estimulada

Liberación de un fotón desencadenada por otro

La luz láser es un tipo de emisión estimulada de radiación.

La emisión estimulada es el proceso por el cual un fotón entrante de una frecuencia específica puede interactuar con un electrón atómico excitado (u otro estado molecular excitado), lo que hace que caiga a un nivel de energía inferior . La energía liberada se transfiere al campo electromagnético, creando un nuevo fotón con una frecuencia , polarización y dirección de viaje que son todas idénticas a los fotones de la onda incidente. Esto contrasta con la emisión espontánea , que ocurre a una tasa característica para cada uno de los átomos/osciladores en el estado de energía superior independientemente del campo electromagnético externo.

Según la American Physical Society , la primera persona en predecir correctamente el fenómeno de la emisión estimulada fue Albert Einstein en una serie de artículos que comenzaron en 1916 y que culminaron en lo que ahora se llama el coeficiente B de Einstein . El trabajo de Einstein se convirtió en la base teórica del máser y el láser . ^{[1] [2] [3] [4]} El proceso es idéntico en forma a la absorción atómica en la que la energía de un fotón absorbido causa una transición atómica idéntica pero opuesta: del nivel inferior a un nivel de energía superior. En medios normales en equilibrio térmico, la absorción excede la emisión estimulada porque hay más electrones en los estados de energía inferior que en los estados de energía superior. Sin embargo, cuando hay una inversión de población , la tasa de emisión estimulada excede la de absorción y se puede lograr una amplificación óptica neta. Un medio de ganancia de este tipo , junto con un resonador óptico, es el corazón de un láser o máser. Al carecer de un mecanismo de retroalimentación, los amplificadores láser y las fuentes superluminiscentes también funcionan sobre la base de la emisión estimulada.

Descripción general

Los electrones y sus interacciones con los campos electromagnéticos son importantes para comprender la química y la física . En la teoría clásica , la energía de un electrón que orbita alrededor de un núcleo atómico es mayor para las órbitas más alejadas del núcleo de un átomo . Sin embargo, los efectos de la mecánica cuántica obligan a los electrones a adoptar posiciones discretas en los orbitales . Por lo tanto, los electrones se encuentran en niveles de energía específicos de un átomo, dos de los cuales se muestran a continuación:

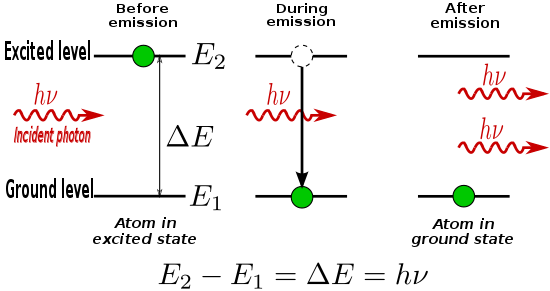
Cuando un electrón absorbe energía, ya sea de luz (fotones) o de calor ( fonones ), recibe ese quantum de energía incidente. Pero las transiciones solo se permiten entre niveles de energía discretos, como los dos que se muestran arriba. Esto da lugar a líneas de emisión y líneas de absorción .

Cuando un electrón se excita desde un nivel de energía más bajo a uno más alto, es poco probable que permanezca así para siempre. Un electrón en un estado excitado puede decaer a un estado de energía más bajo que no esté ocupado, de acuerdo con una constante de tiempo particular que caracteriza esa transición. Cuando un electrón de este tipo se desintegra sin influencia externa, emitiendo un fotón, eso se llama " emisión espontánea ". La fase y la dirección asociadas con el fotón que se emite son aleatorias. Un material con muchos átomos en un estado excitado de este tipo puede dar lugar a una radiación que tiene un espectro estrecho (centrado alrededor de una longitud de onda de luz), pero los fotones individuales no tendrían una relación de fase común y también emanarían en direcciones aleatorias. Este es el mecanismo de fluorescencia y emisión térmica .

Un campo electromagnético externo a una frecuencia asociada con una transición puede afectar el estado mecánico cuántico del átomo sin ser absorbido. A medida que el electrón en el átomo hace una transición entre dos estados estacionarios (ninguno de los cuales muestra un campo dipolar), entra en un estado de transición que sí tiene un campo dipolar, y que actúa como un pequeño dipolo eléctrico , y este dipolo oscila a una frecuencia característica. En respuesta al campo eléctrico externo a esta frecuencia, la probabilidad de que el electrón entre en este estado de transición aumenta considerablemente. Por lo tanto, la tasa de transiciones entre dos estados estacionarios aumenta más allá de la de la emisión espontánea. Una transición del estado de mayor a menor energía produce un fotón adicional con la misma fase y dirección que el fotón incidente; este es el proceso de emisión estimulada.

Historia

La emisión estimulada fue un descubrimiento teórico de Albert Einstein en el marco de la antigua teoría cuántica , en la que la emisión se describe en términos de fotones que son los cuantos del campo EM. ^{[5] [6]} La emisión estimulada también puede ocurrir en modelos clásicos, sin referencia a los fotones o la mecánica cuántica. ^{[7] [ se necesita una fuente no primaria ]} (Véase también Láser § Historia ). Según el profesor de física y director del Centro de Átomos Ultrafríos del MIT-Harvard Daniel Kleppner , la teoría de la radiación de Einstein se adelantó a su tiempo y prefigura la teoría moderna de la electrodinámica cuántica y la óptica cuántica por varias décadas. ^[8]

Modelo matemático

La emisión estimulada se puede modelar matemáticamente considerando un átomo que puede estar en uno de dos estados de energía electrónica, un estado de nivel inferior (posiblemente el estado fundamental) (1) y un estado excitado (2), con energías E ₁ y E ₂ respectivamente.

Si el átomo está en estado excitado, puede decaer al estado inferior mediante el proceso de emisión espontánea , liberando la diferencia de energías entre los dos estados en forma de fotón. El fotón tendrá frecuencia ν ₀ y energía hν ₀ , dadas por: donde h es la constante de Planck . $${\displaystyle E_{2}-E_{1}=h\,\nu _{0}}$$

Alternativamente, si el átomo en estado excitado es perturbado por un campo eléctrico de frecuencia ν ₀ , puede emitir un fotón adicional de la misma frecuencia y en fase, aumentando así el campo externo, dejando al átomo en el estado de energía más bajo. Este proceso se conoce como emisión estimulada.

En un grupo de tales átomos, si el número de átomos en el estado excitado está dado por N ₂ , la tasa a la que ocurre la emisión estimulada está dada por donde la constante de proporcionalidad B ₂₁ se conoce como el coeficiente B de Einstein para esa transición particular, y ρ ( ν ) es la densidad de radiación del campo incidente en la frecuencia ν . La tasa de emisión es, por tanto, proporcional al número de átomos en el estado excitado N ₂ y a la densidad de fotones incidentes. $${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=-B_{21}\,\rho (\nu )\,N_{2}}$$

Al mismo tiempo, se producirá un proceso de absorción atómica que elimina energía del campo mientras eleva los electrones del estado inferior al superior. Su tasa es precisamente el negativo de la tasa de emisión estimulada. $${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=B_{12}\,\rho (\nu )\,N_{1}.}$$

La tasa de absorción es, por tanto, proporcional al número de átomos en el estado inferior, N ₁ . Los coeficientes B se pueden calcular utilizando la aproximación dipolar y la teoría de perturbación dependiente del tiempo en mecánica cuántica como: ^{[9] [10]} donde B corresponde a la distribución de energía en términos de frecuencia ν . El coeficiente B puede variar según la elección de la función de distribución de energía utilizada, sin embargo, el producto de la función de distribución de energía y su respectivo coeficiente B sigue siendo el mismo. $${\displaystyle B_{ab}={\frac {e^{2}}{6\epsilon _{0}\hbar ^{2}}}|\langle a|{\vec {r}}|b\rangle |^{2}}$$

Einstein demostró a partir de la forma de la ley de Planck, ^{[ cita requerida ]} que el coeficiente para esta transición debe ser idéntico al de la emisión estimulada: $${\displaystyle B_{12}=B_{21}.}$$

Por lo tanto, la absorción y la emisión estimulada son procesos inversos que se desarrollan a velocidades algo diferentes. Otra forma de ver esto es considerar la emisión o absorción estimulada neta como un solo proceso. La tasa neta de transiciones de E ₂ a E ₁ debido a este proceso combinado se puede encontrar sumando sus respectivas tasas, que se indican arriba: $${\displaystyle {\frac {\partial N_{1}^{\text{net}}}{\partial t}}=-{\frac {\partial N_{2}^{\text{net}}}{\partial t}}=B_{21}\,\rho (\nu )\,(N_{2}-N_{1})=B_{21}\,\rho (\nu )\,\Delta N.}$$

De esta manera, se libera una potencia neta en el campo eléctrico igual a la energía del fotón hν multiplicada por esta tasa de transición neta. Para que este sea un número positivo, que indica una emisión estimulada neta, debe haber más átomos en el estado excitado que en el nivel inferior: . De lo contrario, hay una absorción neta y la potencia de la onda se reduce durante el paso a través del medio. La condición especial se conoce como inversión de población , una condición bastante inusual que debe producirse en el medio de ganancia de un láser. ${\displaystyle \Delta N>0}$ ${\displaystyle N_{2}>N_{1}}$

La característica notable de la emisión estimulada en comparación con las fuentes de luz cotidianas (que dependen de la emisión espontánea) es que los fotones emitidos tienen la misma frecuencia, fase, polarización y dirección de propagación que los fotones incidentes. Los fotones involucrados son, por lo tanto, mutuamente coherentes . Cuando hay una inversión de población ( ), por lo tanto, se producirá una amplificación óptica de la radiación incidente. ${\displaystyle \Delta N>0}$

Aunque la energía generada por la emisión estimulada siempre está en la frecuencia exacta del campo que la ha estimulado, la ecuación de velocidad anterior se refiere solo a la excitación en la frecuencia óptica particular correspondiente a la energía de la transición. En frecuencias desplazadas de la intensidad de la emisión estimulada (o espontánea) se reducirá de acuerdo con la denominada forma de línea . Considerando solo el ensanchamiento homogéneo que afecta a una resonancia atómica o molecular, la función de forma de línea espectral se describe como una distribución de Lorentz donde es el ancho completo en la mitad del ancho de banda máximo o FWHM. ${\displaystyle \nu _{0}}$ ${\displaystyle \nu _{0}}$ $${\displaystyle g'(\nu )={1 \over \pi }{(\Gamma /2) \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}}$$ ${\displaystyle \Gamma }$

El valor máximo de la forma de línea de Lorentz se produce en el centro de la línea, . Una función de forma de línea se puede normalizar de modo que su valor en sea la unidad; en el caso de un Lorentziano obtenemos ${\displaystyle \nu =\nu _{0}}$ ${\displaystyle \nu _{0}}$ $${\displaystyle g(\nu )={g'(\nu ) \over g'(\nu _{0})}={(\Gamma /2)^{2} \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}.}$$

Por lo tanto, la emisión estimulada a frecuencias alejadas de se reduce por este factor. En la práctica, también puede haber un ensanchamiento de la forma de la línea debido a un ensanchamiento no homogéneo , sobre todo debido al efecto Doppler resultante de la distribución de velocidades en un gas a una temperatura determinada. Esto tiene una forma gaussiana y reduce la intensidad máxima de la función de forma de línea. En un problema práctico, la función de forma de línea completa se puede calcular a través de una convolución de las funciones de forma de línea individuales involucradas. Por lo tanto, la amplificación óptica agregará potencia a un campo óptico incidente a una frecuencia a una tasa dada por ${\displaystyle \nu _{0}}$ ${\displaystyle \nu }$ $${\displaystyle P=h\nu \,g(\nu )\,B_{21}\,\rho (\nu )\,\Delta N.}$$

Sección transversal de emisión estimulada

La sección transversal de emisión estimulada es donde $${\displaystyle \sigma _{21}(\nu )=A_{21}{\frac {\lambda ^{2}}{8\pi n^{2}}}g'(\nu )}$$

• A ₂₁ es el coeficiente de Einstein A ,
• λ es la longitud de onda en el vacío,
• n es el índice de refracción del medio (adimensional), y
• g ′( ν ) es la función de forma de la línea espectral.

Amplificación óptica

La emisión estimulada puede proporcionar un mecanismo físico para la amplificación óptica . Si una fuente externa de energía estimula a más del 50% de los átomos en el estado fundamental para que pasen al estado excitado, se crea lo que se denomina una inversión de población . Cuando la luz de la frecuencia adecuada pasa a través del medio invertido, los fotones son absorbidos por los átomos que permanecen en el estado fundamental o los fotones estimulan a los átomos excitados para que emitan fotones adicionales de la misma frecuencia, fase y dirección. Dado que hay más átomos en el estado excitado que en el estado fundamental, se produce una amplificación de la intensidad de entrada .

La inversión de población, en unidades de átomos por metro cúbico, es

${\displaystyle \Delta N_{21}=N_{2}-{g_{2} \over g_{1}}N_{1}}$

donde g ₁ y g ₂ son las degeneraciones de los niveles de energía 1 y 2, respectivamente.

Ecuación de ganancia de señal pequeña

La intensidad (en vatios por metro cuadrado) de la emisión estimulada está determinada por la siguiente ecuación diferencial:

${\displaystyle {dI \over dz}=\sigma _{21}(\nu )\cdot \Delta N_{21}\cdot I(z)}$

siempre que la intensidad I ( z ) sea lo suficientemente pequeña como para que no tenga un efecto significativo en la magnitud de la inversión de la población. Agrupando los dos primeros factores, esta ecuación se simplifica como

${\displaystyle {dI \over dz}=\gamma _{0}(\nu )\cdot I(z)}$

dónde

${\displaystyle \gamma _{0}(\nu )=\sigma _{21}(\nu )\cdot \Delta N_{21}}$

es el coeficiente de ganancia de señal pequeña (en unidades de radianes por metro). Podemos resolver la ecuación diferencial mediante separación de variables :

${\displaystyle {dI \over I(z)}=\gamma _{0}(\nu )\cdot dz}$

Integrando, encontramos:

${\displaystyle \ln \left({I(z) \over I_{in}}\right)=\gamma _{0}(\nu )\cdot z}$

o

${\displaystyle I(z)=I_{in}e^{\gamma _{0}(\nu )z}}$

dónde

${\displaystyle I_{in}=I(z=0)\,}$es la intensidad óptica de la señal de entrada (en vatios por metro cuadrado).

Intensidad de saturación

La intensidad de saturación I _S se define como la intensidad de entrada en la que la ganancia del amplificador óptico cae exactamente a la mitad de la ganancia de señal pequeña. Podemos calcular la intensidad de saturación como

${\displaystyle I_{S}={h\nu \over \sigma (\nu )\cdot \tau _{S}}}$

dónde

${\displaystyle h}$es la constante de Planck , y

${\displaystyle \tau _{\text{S}}}$es la constante de tiempo de saturación, que depende de los tiempos de vida de las emisiones espontáneas de las distintas transiciones entre los niveles de energía relacionados con la amplificación.

${\displaystyle \nu }$es la frecuencia en Hz

El valor mínimo de se produce en resonancia, ^[11] donde la sección transversal es la más grande. Este valor mínimo es: ${\displaystyle I_{\text{S}}(\nu )}$ ${\displaystyle \sigma (\nu )}$

${\displaystyle I_{\text{sat}}={\frac {\pi }{3}}{hc \over \lambda ^{3}\tau _{S}}}$

Para un átomo simple de dos niveles con un ancho de línea natural , la constante de tiempo de saturación es . ${\displaystyle \Gamma }$ ${\displaystyle \tau _{\text{S}}=\Gamma ^{-1}}$

Ecuación de ganancia general

La forma general de la ecuación de ganancia, que se aplica independientemente de la intensidad de entrada, se deriva de la ecuación diferencial general para la intensidad I en función de la posición z en el medio de ganancia :

${\displaystyle {dI \over dz}={\gamma _{0}(\nu ) \over 1+{\bar {g}}(\nu ){I(z) \over I_{S}}}\cdot I(z)}$

donde es la intensidad de saturación. Para resolver, primero reordenamos la ecuación para separar las variables, intensidad I y posición z : ${\displaystyle I_{S}}$

${\displaystyle {dI \over I(z)}\left[1+{\bar {g}}(\nu ){I(z) \over I_{S}}\right]=\gamma _{0}(\nu )\cdot dz}$

Integrando ambos lados, obtenemos

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I(z)-I_{in} \over I_{S}}=\gamma _{0}(\nu )\cdot z}$

o

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left({I(z) \over I_{in}}-1\right)=\gamma _{0}(\nu )\cdot z}$

La ganancia G del amplificador se define como la intensidad óptica I en la posición z dividida por la intensidad de entrada:

${\displaystyle G=G(z)={I(z) \over I_{in}}}$

Sustituyendo esta definición en la ecuación anterior, encontramos la ecuación de ganancia general :

${\displaystyle \ln \left(G\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left(G-1\right)=\gamma _{0}(\nu )\cdot z}$

Aproximación de señal pequeña

En el caso especial donde la señal de entrada es pequeña en comparación con la intensidad de saturación, en otras palabras,

${\displaystyle I_{in}\ll I_{S}\,}$

Entonces la ecuación de ganancia general da la ganancia de señal pequeña como

${\displaystyle \ln(G)=\ln(G_{0})=\gamma _{0}(\nu )\cdot z}$

o

${\displaystyle G=G_{0}=e^{\gamma _{0}(\nu )z}}$

que es idéntica a la ecuación de ganancia de señal pequeña (ver arriba).

Comportamiento asintótico de señales grandes

Para señales de entrada grandes, donde

${\displaystyle I_{in}\gg I_{S}\,}$

La ganancia se acerca a la unidad

${\displaystyle G\rightarrow 1}$

y la ecuación de ganancia general se aproxima a una asíntota lineal :

${\displaystyle I(z)=I_{in}+{\gamma _{0}(\nu )\cdot z \over {\bar {g}}(\nu )}I_{S}}$

Véase también

• Absorción
• Medio láser activo
• Láser (incluye una sección de historia )
• Ciencia del láser
• Ciclo de Rabi
• Emisión espontánea
• Microscopía STED
• Coeficientes de Einstein

Referencias

1. Tretkoff, Ernie (agosto de 2005). «Este mes en la historia de la física: Einstein predice la emisión estimulada». American Physical Society News . 14 (8) . Consultado el 1 de junio de 2022 .
2. Straumann, Norbert (23 de marzo de 2017). "Einstein en 1916: "Sobre la teoría cuántica de la radiación"". arXiv : 1703.08176 [física.hist-ph].
3. Hecht, Jeff (15 de agosto de 2021). «Laser». Enciclopedia Británica . Consultado el 1 de junio de 2022 .
4. Stone, A. Douglas (6 de octubre de 2013). Einstein y lo cuántico: la búsqueda del valiente suabo (primera edición). Princeton University Press. ISBN 978-0691139685. Recuperado el 1 de junio de 2022 .
5. Einstein, A (1916). "Strahlungs-emisión y absorción nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft . 18 : 318–323. Código Bib : 1916DPhyG..18..318E.
6. Einstein, A (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift . 18 : 121-128. Código bibliográfico : 1917PhyZ...18..121E.
7. Fain, B.; Milonni, PW (1987). "Emisión estimulada clásica". Revista de la Sociedad Óptica de América B . 4 (1): 78. Bibcode :1987JOSAB...4...78F. doi :10.1364/JOSAB.4.000078.
8. Kleppner, Daniel (1 de febrero de 2005). "Releyendo a Einstein sobre la radiación". Physics Today . 58 (2): 30–33. Bibcode :2005PhT....58b..30K. doi :10.1063/1.1897520 . Consultado el 1 de junio de 2022 .
9. Hilborn, Robert (2002). "Coeficientes de Einstein, secciones eficaces, valores f, momentos dipolares y todo eso" (PDF) .
10. Segre, Carlo. "Los coeficientes de Einstein - Fundamentos de la teoría cuántica II (PHYS 406)" (PDF) . pág. 32.
11. Foot, CJ (2005). Física atómica. Oxford University Press. pág. 142. ISBN 978-0-19-850695-9.

• Saleh, Bahaa EA y Teich, Malvin Carl (1991). Fundamentos de Fotónica . Nueva York: John Wiley & Sons. ISBN 0-471-83965-5.
• Alan Corney (1977). Espectroscopia atómica y láser . Oxford: Oxford Uni. Press. ISBN 0-19-921145-0. Libro  de bolsillo de la editorial.