Mojada

Capacidad de un líquido para mantener contacto con una superficie sólida.

Gota de agua sobre un tejido que se ha vuelto no humectable mediante un tratamiento químico.

La humectación es la capacidad de un líquido de desplazar un gas para mantener el contacto con una superficie sólida , resultado de las interacciones intermoleculares cuando ambos se juntan. ^[1] Esto sucede en presencia de una fase gaseosa u otra fase líquida no miscible con la primera. El grado de humectación (humectabilidad) está determinado por un equilibrio de fuerzas entre las fuerzas adhesivas y cohesivas . Existen dos tipos de humectación: humectación no reactiva y humectación reactiva. ^{[2] [3]}

La humectación es importante para la unión o adherencia de dos materiales. ^[4] La humectación y las fuerzas superficiales que la controlan también son responsables de otros efectos relacionados, incluidos los efectos capilares . Los surfactantes se pueden utilizar para aumentar el poder humectante de un líquido como el agua.

La humectación es un foco de atención en los estudios de nanotecnología y nanociencia debido a la aparición de muchos nanomateriales en las últimas dos décadas (por ejemplo, grafeno , ^[5] nanotubo de carbono , nanomalla de nitruro de boro ^[6] ).

Explicación

Figura 1: Ángulo de contacto de una gota de líquido sobre una superficie sólida

Las fuerzas adhesivas entre un líquido y un sólido hacen que una gota de líquido se extienda por la superficie. Las fuerzas de cohesión dentro del líquido hacen que la gota se aglomere y evite el contacto con la superficie.

Figura 2: Humectación de diferentes fluidos: A muestra un fluido con muy poca humectación, mientras que C muestra un fluido con más humectación. A tiene un ángulo de contacto grande y C tiene un ángulo de contacto pequeño.

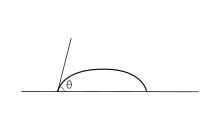
El ángulo de contacto (θ), como se ve en la Figura 1, es el ángulo en el que la interfaz líquido-vapor se encuentra con la interfaz sólido-líquido. El ángulo de contacto está determinado por el equilibrio entre las fuerzas adhesivas y cohesivas. A medida que aumenta la tendencia de una gota a extenderse sobre una superficie plana y sólida, el ángulo de contacto disminuye. Por lo tanto, el ángulo de contacto proporciona una medida inversa de la humectabilidad. ^{[7] [8]}

Un ángulo de contacto inferior a 90° (ángulo de contacto bajo) suele indicar que la humectación de la superficie es muy favorable y que el fluido se esparcirá sobre una gran área de la superficie. Los ángulos de contacto superiores a 90° (ángulo de contacto alto) generalmente significan que la humectación de la superficie es desfavorable, por lo que el fluido minimizará el contacto con la superficie y formará una gota de líquido compacta.

En el caso del agua, una superficie humectable también puede denominarse hidrófila y una superficie no humectable hidrófoba . Las superficies superhidrofóbicas tienen ángulos de contacto mayores de 150°, lo que muestra que casi no hay contacto entre la gota de líquido y la superficie. Esto a veces se conoce como el " efecto Lotus ". La tabla describe los diferentes ángulos de contacto y sus correspondientes interacciones sólido/líquido y líquido/líquido. ^[9] En el caso de líquidos no acuosos, el término liófilo se utiliza para condiciones de ángulo de contacto bajo y liófobo se utiliza cuando resultan ángulos de contacto más altos. De manera similar, los términos omnifóbico y omnifílico se aplican tanto a líquidos polares como apolares.

Superficies de alta energía vs. superficies de baja energía

Los líquidos pueden interactuar con dos tipos principales de superficies sólidas. Tradicionalmente, las superficies sólidas se han dividido en sólidos de alta energía y sólidos de baja energía. La energía relativa de un sólido tiene que ver con la naturaleza volumétrica del sólido en sí. Los sólidos como los metales, los vidrios y las cerámicas se conocen como "sólidos duros" porque los enlaces químicos que los mantienen unidos (por ejemplo, covalentes , iónicos o metálicos ) son muy fuertes. Por lo tanto, se necesita una gran cantidad de energía para romper estos sólidos (alternativamente, se requiere una gran cantidad de energía para cortar la masa y hacer dos superficies separadas), por lo que se denominan "de alta energía". La mayoría de los líquidos moleculares logran una humectación completa con superficies de alta energía.

El otro tipo de sólido son los cristales moleculares débiles (por ejemplo, fluorocarbonos , hidrocarburos , etc.) en los que las moléculas se mantienen unidas esencialmente por fuerzas físicas (por ejemplo, fuerzas de van der Waals y enlaces de hidrógeno ). Dado que estos sólidos se mantienen unidos por fuerzas débiles, se requiere una cantidad muy baja de energía para romperlos, por lo que se denominan "de baja energía". Dependiendo del tipo de líquido elegido, las superficies de baja energía pueden permitir una humectación total o parcial. ^{[10] [11]}

Se ha informado de superficies dinámicas que experimentan cambios en la energía superficial al aplicarles un estímulo apropiado. Por ejemplo, se ha demostrado que una superficie que presenta motores moleculares impulsados ​​por fotones experimenta cambios en el ángulo de contacto con el agua cuando se cambia entre conformaciones biestables de diferentes energías superficiales. ^[12]

Humectación de superficies de baja energía

Las superficies de baja energía interactúan principalmente con líquidos a través de fuerzas dispersivas ( de van der Waals ). William Zisman produjo varios hallazgos clave: ^[13]

Zisman observó que el cos θ aumenta linealmente a medida que la tensión superficial (γ _LV ) del líquido disminuye. De esta manera, pudo establecer una función lineal entre el cos θ y la tensión superficial (γ _LV ) para varios líquidos orgánicos .

Una superficie es más humectable cuando γ _LV y θ son bajos. Zisman denominó la intersección de estas líneas cuando cos θ = 1 como la tensión superficial crítica (γ _c ) de esa superficie. Esta tensión superficial crítica es un parámetro importante porque es una característica exclusiva del sólido.

Conociendo la tensión superficial crítica de un sólido, es posible predecir la humectabilidad de la superficie. ^[7] La ​​humectabilidad de una superficie está determinada por los grupos químicos más externos del sólido. Las diferencias en humectabilidad entre superficies que son similares en estructura se deben a diferencias en el empaquetamiento de los átomos. Por ejemplo, si una superficie tiene cadenas ramificadas, tendrá un empaquetamiento más pobre que una superficie con cadenas rectas. Una tensión superficial crítica más baja significa una superficie de material menos humectable.

Superficies sólidas ideales

Una superficie ideal es plana, rígida, perfectamente lisa, químicamente homogénea y tiene histéresis de ángulo de contacto cero . La histéresis cero implica que los ángulos de contacto de avance y retroceso son iguales. En otras palabras, solo existe un ángulo de contacto termodinámicamente estable. Cuando se coloca una gota de líquido sobre una superficie de este tipo, se forma el ángulo de contacto característico como se muestra en la Figura 1. Además, en una superficie ideal, la gota volverá a su forma original si se altera. ^{[9] [13]} Las siguientes derivaciones se aplican solo a superficies sólidas ideales; solo son válidas para el estado en el que las interfaces no se mueven y la línea límite de fase existe en equilibrio.

Minimización de energía, tres fases

Figura 3: Coexistencia de tres fases de fluido en contacto mutuo; aquí, α, β y θ indican cada uno una fase y su ángulo de contacto.

Figura 4: Triángulo de Neumann que relaciona las energías superficiales y los ángulos de contacto de tres fases de fluido que coexisten en equilibrio estático, como se muestra en la Figura 3

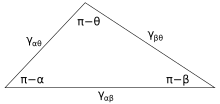
La figura 3 muestra la línea de contacto donde se encuentran las tres fases. En equilibrio , la fuerza neta por unidad de longitud que actúa a lo largo de la línea límite entre las tres fases debe ser cero. Los componentes de la fuerza neta en la dirección a lo largo de cada una de las interfaces se dan por:

${\displaystyle {\begin{aligned}\gamma _{\alpha \theta }+\gamma _{\theta \beta }\cos \left(\theta \right)+\gamma _{\alpha \beta }\cos \left(\alpha \right)&=0\\\gamma _{\alpha \theta }\cos \left(\theta \right)+\gamma _{\theta \beta }+\gamma _{\alpha \beta }\cos \left(\beta \right)&=0\\\gamma _{\alpha \theta }\cos \left(\alpha \right)+\gamma _{\theta \beta }\cos \left(\beta \right)+\gamma _{\alpha \beta }&=0\end{aligned}}}$

donde α, β y θ son los ángulos mostrados y γ _ij es la energía superficial entre las dos fases indicadas. Estas relaciones también se pueden expresar mediante un análogo a un triángulo conocido como triángulo de Neumann, que se muestra en la Figura 4. El triángulo de Neumann es consistente con la restricción geométrica de que , y al aplicarle la ley de senos y la ley de cosenos se producen relaciones que describen cómo los ángulos interfaciales dependen de las relaciones de las energías superficiales. ^[14] ${\displaystyle \alpha +\beta +\theta =2\pi }$

Como estas tres energías superficiales forman los lados de un triángulo , están limitadas por las desigualdades del triángulo, γ _ij < γ _jk + γ _ik, lo que significa que ninguna de las tensiones superficiales puede superar la suma de las otras dos. Si se ponen en contacto tres fluidos con energías superficiales que no siguen estas desigualdades, no existirá ninguna configuración de equilibrio coherente con la Figura 3.

Simplificación a geometría plana, relación de Young

Figura 5: Ángulo de contacto de una gota de líquido humedecida con una superficie sólida rígida

Si la fase β se reemplaza por una superficie rígida plana, como se muestra en la Figura 5, entonces β = π, y la segunda ecuación de fuerza neta se simplifica a la ecuación de Young, ^[15]

${\displaystyle \gamma _{SG}=\gamma _{SL}+\gamma _{LG}\cos \left(\theta \right)}$^[16]

que relaciona las tensiones superficiales entre las tres fases: sólido , líquido y gaseoso . Posteriormente, esto predice el ángulo de contacto de una gota de líquido sobre una superficie sólida a partir del conocimiento de las tres energías superficiales involucradas. Esta ecuación también se aplica si la fase "gas" es otro líquido, inmiscible con la gota de la primera fase "líquida".

Simplificación a geometría plana, relación de Young derivada del cálculo variacional

Considere la interfaz como una curva para donde es un parámetro libre. La energía libre que se debe minimizar es ${\displaystyle y(x)}$ ${\displaystyle x\in I=[0,L]}$ ${\displaystyle L}$

${\displaystyle {\cal {F}}[y,L]=\int _{0}^{L}\left(\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})\right)dx}$

con las restricciones que podemos escribir como y volumen fijo . ${\displaystyle y(0)=y(L)=0}$ ${\displaystyle \int _{I}y'dx=0}$ ${\displaystyle \int _{I}ydx=A}$

El lagrangiano modificado, teniendo en cuenta las restricciones, es por tanto

${\displaystyle {\cal {L}}=\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})-\lambda _{1}y'-\lambda _{2}y}$

donde son los multiplicadores de Lagrange. Por definición, el momento y el hamiltoniano que se calculan son: ${\displaystyle \lambda _{i}}$ ${\displaystyle p=\partial _{y'}{\cal {L}}}$ ${\displaystyle {\cal {H}}=py'-{\cal {L}}}$

${\displaystyle {\cal {H}}=-\gamma _{LG}{\frac {1}{\sqrt {1+y'^{2}}}}-(\gamma _{SL}-\gamma _{SG})+\lambda _{2}y}$

Ahora, recordemos que el límite es libre en la dirección y es un parámetro libre. Por lo tanto, debemos tener: ${\displaystyle x}$ ${\displaystyle L}$

${\displaystyle {\frac {\partial {\cal {F}}}{\partial L}}=-{\cal {H}}=0}$

En el límite y , por lo tanto recuperamos la ecuación de Young. ${\displaystyle y(L)=0}$ ${\displaystyle (1+y'^{2})^{-1/2}=\cos \theta }$

Superficies lisas no ideales y ángulo de contacto de Young

La ecuación de Young supone una superficie perfectamente plana y rígida, a menudo denominada superficie ideal . En muchos casos, las superficies están lejos de esta situación ideal, y aquí se consideran dos: el caso de superficies rugosas y el caso de superficies lisas que siguen siendo reales (finitamente rígidas). Incluso en una superficie perfectamente lisa, una gota asumirá un amplio espectro de ángulos de contacto que van desde el llamado ángulo de contacto de avance, , hasta el llamado ángulo de contacto de retroceso, . El ángulo de contacto de equilibrio ( ) se puede calcular a partir de y como lo demostró Tadmor ^[17] como, ${\displaystyle \theta _{\mathrm {A} }}$ ${\displaystyle \theta _{\mathrm {R} }}$ ${\displaystyle \theta _{\mathrm {c} }}$ ${\displaystyle \theta _{\mathrm {A} }}$ ${\displaystyle \theta _{\mathrm {R} }}$

${\displaystyle \theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos \left(\theta _{\mathrm {A} }\right)+r_{\mathrm {R} }\cos \left(\theta _{\mathrm {R} }\right)}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)}$

dónde

${\displaystyle r_{\mathrm {A} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {A} }\right)}{2-3\cos \left(\theta _{\mathrm {A} }\right)+\cos ^{3}\left(\theta _{\mathrm {A} }\right)}}\right)^{\frac {1}{3}}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {R} }\right)}{2-3\cos \left(\theta _{\mathrm {R} }\right)+\cos ^{3}\left(\theta _{\mathrm {R} }\right)}}\right)^{\frac {1}{3}}}$

La ecuación de Young-Dupré y el coeficiente de propagación

La ecuación de Young-Dupré ( Thomas Young 1805; Anthanase Dupré y Paul Dupré 1869) dicta que ni γ _SG ni γ _SL pueden ser mayores que la suma de las otras dos energías superficiales. ^{[18] [19]} La consecuencia de esta restricción es la predicción de humectación completa cuando γ _SG > γ _SL + γ _LG y humectación cero cuando γ _SL > γ _SG + γ _LG . La falta de una solución para la ecuación de Young-Dupré es un indicador de que no existe una configuración de equilibrio con un ángulo de contacto entre 0 y 180° para esas situaciones. ^[20]

Un parámetro útil para medir la humectación es el parámetro de propagación S ,

${\displaystyle S=\gamma _{SG}-\left(\gamma _{SL}+\gamma _{LG}\right)}$

Cuando S > 0, el líquido humedece completamente la superficie (humectación completa). Cuando S < 0, se produce una humectación parcial.

Combinando la definición del parámetro de propagación con la relación de Young se obtiene la ecuación de Young-Dupré:

${\displaystyle S=\gamma _{LG}\left(\cos \left(\theta \right)-1\right)}$

que sólo tiene soluciones físicas para θ cuando S < 0.

Un modelo generalizado para el ángulo de contacto de las gotas en superficies planas y curvas

Con las mejoras en las técnicas de medición, como el microscopio de movimiento axial (AFM), la microscopía confocal y el microscopio electrónico de barrido (SEM), los investigadores pudieron producir y obtener imágenes de gotitas a escalas cada vez más pequeñas. Con la reducción del tamaño de las gotitas se obtuvieron nuevas observaciones experimentales de humectación. Estas observaciones confirman que la ecuación de Young modificada ^[21] no se cumple en las escalas micro y nanométricas. Además, el signo de la tensión de la línea no se mantiene a través de la ecuación de Young modificada. ^[22]

Para una gota sésil, la energía libre del sistema trifásico se puede expresar como: ^{[23] [24]}

${\displaystyle \delta w=\gamma _{LV}dA_{LV}+\gamma _{SL}dA_{SL}+\gamma _{SV}dA_{SV}-\kappa dL-PdV-VdP}$

A volumen constante en equilibrio termodinámico, esto se reduce a: ^[25]

${\displaystyle 0={\frac {dA_{LG}}{dA_{SL}}}+{\frac {\gamma _{SL}-\gamma _{SG}}{\gamma _{LG}}}-{\frac {\kappa }{\gamma _{LG}}}{\frac {dL}{dA_{SL}}}-{\frac {V}{\gamma _{LG}}}{\frac {dP}{dA_{SL}}}}$

Por lo general, el término VdP se ha descuidado para gotas grandes; sin embargo, el trabajo de VdP se vuelve significativo a escalas pequeñas. La variación de la presión a volumen constante en el límite líquido-vapor libre se debe a la presión de Laplace , que es proporcional a la curvatura media de la gota y no es cero. Al resolver la ecuación anterior para superficies convexas y cóncavas, se obtiene: ^[26]

${\displaystyle \cos(\theta \mp \alpha )=A+B{\frac {\cos(\alpha )}{a}}\pm C\sin(\theta \mp \alpha )(\cos(\theta )+1)^{2}{\biggl (}{\frac {\sin(\alpha )(\cos(\alpha )+2)}{(\cos(\alpha )+1)^{2}}}\mp {\frac {\sin(\theta )(\cos(\theta )+2)}{(\cos(\theta )+1)^{2}}}{\biggr )}}$

Donde los parámetros constantes A, B y C se definen como:

Diagramas esquemáticos de gotas en superficies planas (a), cóncavas (b) y convexas (c) ^[26]

${\displaystyle A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}}$, y ${\displaystyle B={\frac {\kappa }{\gamma _{LG}}}}$ ${\displaystyle C={\frac {\gamma }{3\gamma _{LG}}}}$

Esta ecuación relaciona el ángulo de contacto , una propiedad geométrica de una gota sésil con la termodinámica en masa, la energía en el límite de contacto trifásico y la curvatura de la superficie α. Para el caso especial de una gota sésil sobre una superficie plana (α=0), ${\displaystyle \theta }$

${\displaystyle \cos(\theta )={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}+{\frac {\kappa }{\gamma _{LG}}}{\frac {1}{a}}-{\frac {\gamma }{3\gamma _{LG}}}(2+\cos(\theta )-2\cos ^{2}(\theta )-\cos ^{3}(\theta ))}$

Los dos primeros términos son la ecuación de Young modificada, ^[21] mientras que el tercer término se debe a la presión de Laplace. Esta ecuación no lineal predice correctamente el signo y la magnitud de κ, el aplanamiento del ángulo de contacto a escalas muy pequeñas y la histéresis del ángulo de contacto. ^{[26] [22]}

Predicción computacional de la humectación

Para muchas configuraciones de superficie/adsorbato, no se dispone de datos de energía superficial ni de observaciones experimentales. Como las interacciones de humectación son de gran importancia en diversas aplicaciones, a menudo se desea predecir y comparar el comportamiento de humectación de varias superficies de materiales con orientaciones cristalográficas particulares, en relación con el agua u otros adsorbatos. Esto se puede hacer desde una perspectiva atomística con herramientas que incluyen dinámica molecular y teoría funcional de la densidad . ^{[27] [28]} En la predicción teórica de la humectación mediante enfoques ab initio como DFT, el hielo se sustituye comúnmente por agua. Esto se debe a que los cálculos de DFT generalmente se realizan asumiendo condiciones de movimiento térmico cero de átomos, lo que esencialmente significa que la simulación se realiza en cero absoluto . Sin embargo, esta simplificación produce resultados que son relevantes para la adsorción de agua en condiciones realistas y el uso de hielo para la simulación teórica de la humectación es común. ^[29]

Superficies sólidas rugosas no ideales

Figura 6: Esquema de los ángulos de contacto de avance y retroceso.

A diferencia de las superficies ideales, las superficies reales no tienen una suavidad, rigidez u homogeneidad química perfectas. Estas desviaciones de la idealidad dan lugar a un fenómeno denominado histéresis del ángulo de contacto , que se define como la diferencia entre los ángulos de contacto de avance (θ _a ) y de retroceso (θ _r ) ^[30]

${\displaystyle {\text{H}}=\,\theta _{a}-\,\theta _{r}}$

Cuando el ángulo de contacto está entre los casos de avance y retroceso, se considera que la línea de contacto está fijada y se puede observar un comportamiento histérico, es decir, la histéresis del ángulo de contacto . Cuando se superan estos valores, el desplazamiento de la línea de contacto, como el de la Figura 3, se producirá por expansión o retracción de la gota. ^[31] La Figura 6 representa los ángulos de contacto de avance y retroceso. El ángulo de contacto de avance es el ángulo estable máximo, mientras que el ángulo de contacto de retroceso es el ángulo estable mínimo. La histéresis del ángulo de contacto se produce porque se encuentran muchos ángulos de contacto termodinámicamente estables diferentes en un sólido no ideal. Estos ángulos de contacto termodinámicamente estables variables se conocen como estados metaestables. ^[13]

Este movimiento de un límite de fase, que implica ángulos de contacto que avanzan y retroceden, se conoce como humectación dinámica. La diferencia entre los ángulos de humectación dinámicos y estáticos es proporcional al número capilar , , Cuando una línea de contacto avanza, cubriendo más superficie con líquido, el ángulo de contacto aumenta y generalmente está relacionado con la velocidad de la línea de contacto. ^{[31] [32]} Si la velocidad de una línea de contacto aumenta sin límite, el ángulo de contacto aumenta y, a medida que se acerca a 180°, la fase gaseosa quedará atrapada en una capa delgada entre el líquido y el sólido. Este es un efecto de desequilibrio cinético que resulta de la línea de contacto que se mueve a una velocidad tan alta que no puede ocurrir una humectación completa. ${\displaystyle Ca}$

Una desviación conocida de las condiciones ideales es cuando la superficie de interés tiene una textura rugosa. La textura rugosa de una superficie puede caer en una de dos categorías: homogénea o heterogénea. Un régimen de humectación homogéneo es aquel en el que el líquido rellena las ranuras de una superficie rugosa. Sin embargo, un régimen de humectación heterogéneo es aquel en el que la superficie es una composición de dos tipos de parches. Un ejemplo importante de una superficie compuesta de este tipo es una compuesta de parches tanto de aire como de sólido. Estas superficies tienen diversos efectos en los ángulos de contacto de los líquidos humectantes. Cassie-Baxter y Wenzel son los dos modelos principales que intentan describir la humectación de superficies texturizadas. Sin embargo, estas ecuaciones solo se aplican cuando el tamaño de la gota es suficientemente grande en comparación con la escala de rugosidad de la superficie. ^[33] Cuando el tamaño de la gota es comparable al de los pilares subyacentes, se debe considerar el efecto de la tensión de la línea. ^[34]

El modelo de Wenzel

Figura 7: Modelo de Wenzel

El modelo de Wenzel ^[35] describe el régimen de humectación homogéneo, como se ve en la Figura 7, y está definido por la siguiente ecuación para el ángulo de contacto en una superficie rugosa: ^[36]

${\displaystyle \cos \,\left(\theta ^{*}\right)=r\cos \,\left(\theta \right)}$

donde es el ángulo de contacto aparente que corresponde al estado de equilibrio estable (es decir, el estado de energía libre mínima para el sistema). La relación de rugosidad, r, es una medida de cómo la rugosidad de la superficie afecta a una superficie homogénea. La relación de rugosidad se define como la relación entre el área real de la superficie sólida y el área aparente. ${\displaystyle \theta ^{*}}$

θ es el ángulo de contacto de un sistema en equilibrio termodinámico, definido para una superficie perfectamente plana. Aunque la ecuación de Wenzel demuestra que el ángulo de contacto de una superficie rugosa es diferente del ángulo de contacto intrínseco, no describe la histéresis del ángulo de contacto . ^[36]

Modelo de Cassie-Baxter

Figura 8: Modelo de Cassie-Baxter

Cuando se trata de una superficie heterogénea, el modelo de Wenzel no es suficiente. Se necesita un modelo más complejo para medir cómo cambia el ángulo de contacto aparente cuando intervienen varios materiales. Esta superficie heterogénea, como la que se ve en la Figura 8, se explica mediante la ecuación de Cassie-Baxter ( ley de Cassie ): ^[33]

${\displaystyle \cos \,\left(\theta ^{*}\right)=r_{f}\,f\,\cos \,\left(\theta _{\text{Y}}\right)+f-1}$

Aquí, r _f es la relación de rugosidad del área de la superficie húmeda y f es la fracción del área de la superficie sólida mojada por el líquido. Cuando f = 1 y r _f = r , las ecuaciones de Cassie-Baxter se convierten en la ecuación de Wenzel. Por otro lado, cuando hay muchas fracciones diferentes de rugosidad de la superficie, cada fracción del área de la superficie total se denota por . ${\displaystyle f_{i}}$

La suma de todos los valores es igual a 1 o la superficie total. Cassie-Baxter también se puede reformular en la siguiente ecuación: ^[37] ${\displaystyle f_{i}}$

${\displaystyle \gamma \cos \,\left(\theta ^{*}\right)=\sum _{n=1}^{N}f_{i}\left(\gamma _{\text{i,sv}}-\gamma _{\text{i,sl}}\right)}$

Aquí se muestra la tensión superficial de Cassie-Baxter entre el líquido y el vapor, es la tensión superficial del vapor sólido de cada componente y es la tensión superficial del líquido sólido de cada componente. Un caso que vale la pena mencionar es cuando la gota de líquido se coloca sobre el sustrato y crea pequeñas bolsas de aire debajo de ella. Este caso para un sistema de dos componentes se denota por: ^[37] ${\displaystyle \gamma }$ ${\displaystyle \gamma _{i,sv}}$ ${\displaystyle \gamma _{i,sl}}$

${\displaystyle \gamma \cos \,\left(\theta ^{*}\right)=f_{1}\left(\gamma _{\text{1,sv}}-\gamma _{\text{1,sl}}\right)-\left(1-f_{1}\right)\gamma }$

Aquí la diferencia clave a notar es que no hay tensión superficial entre el sólido y el vapor para el segundo componente de tensión superficial. Esto se debe a la suposición de que la superficie del aire que está expuesta está debajo de la gota y es el único otro sustrato en el sistema. Posteriormente, la ecuación se expresa como (1 – f ). Por lo tanto, la ecuación de Cassie se puede derivar fácilmente de la ecuación de Cassie-Baxter. Los resultados experimentales con respecto a las propiedades de superficie de los sistemas Wenzel versus Cassie-Baxter mostraron el efecto de la fijación para un ángulo de Young de 180 a 90°, una región clasificada bajo el modelo de Cassie-Baxter. Este sistema compuesto líquido/aire es en gran parte hidrófobo. Después de ese punto, se encontró una transición aguda al régimen de Wenzel donde la gota moja la superficie, pero no más allá de los bordes de la gota. En realidad, las ecuaciones de Young, Wenzel y Cassie-Baxter representan las condiciones de transversalidad del problema variacional de humectación. ^{[38] [39]}

Película precursora

Con la llegada de la imagen de alta resolución, los investigadores han comenzado a obtener datos experimentales que los han llevado a cuestionar los supuestos de la ecuación de Cassie-Baxter al calcular el ángulo de contacto aparente. Estos grupos ^{[ ¿quiénes? ]} creen que el ángulo de contacto aparente depende en gran medida de la línea triple. La línea triple, que está en contacto con la superficie heterogénea, no puede reposar sobre la superficie heterogénea como el resto de la gota. En teoría, debería seguir la imperfección de la superficie. Esta curvatura en la línea triple es desfavorable y no se observa en situaciones del mundo real. Una teoría que preserva la ecuación de Cassie-Baxter y al mismo tiempo explica la presencia del estado de energía minimizado de la línea triple depende de la idea de una película precursora. Esta película de espesor submicrométrico avanza por delante del movimiento de la gota y se encuentra alrededor de la línea triple. Además, esta película precursora permite que la línea triple se doble y adopte diferentes conformaciones que originalmente se consideraron desfavorables. Este fluido precursor se ha observado utilizando microscopía electrónica de barrido ambiental (ESEM) en superficies con poros formados en la masa. Con la introducción del concepto de película precursora, la línea triple puede seguir conformaciones energéticamente factibles, explicando así correctamente el modelo de Cassie-Baxter. ^[40]

“Efecto pétalo” vs. “efecto loto”

Figura 9: “Efecto pétalo” vs. “efecto loto”

La hidrofobicidad intrínseca de una superficie se puede mejorar al texturizarla con diferentes escalas de longitud de rugosidad . La rosa roja aprovecha esto al utilizar una jerarquía de micro y nanoestructuras en cada pétalo para proporcionar suficiente rugosidad para la superhidrofobicidad. Más específicamente, cada pétalo de rosa tiene una colección de micropapilas en la superficie y cada papila, a su vez, tiene muchos nanopliegues. El término " efecto pétalo " describe el hecho de que una gota de agua en la superficie de un pétalo de rosa tiene forma esférica, pero no puede deslizarse incluso si el pétalo se da vuelta. Las gotas de agua mantienen su forma esférica debido a la superhidrofobicidad del pétalo (ángulo de contacto de aproximadamente 152,4°), pero no se deslizan porque la superficie del pétalo tiene una alta fuerza adhesiva con el agua. ^[41]

Al comparar el " efecto pétalo " con el " efecto loto ", es importante observar algunas diferencias llamativas. La estructura de la superficie de la hoja de loto y del pétalo de rosa, como se ve en la Figura 9, se puede utilizar para explicar los dos efectos diferentes.

La hoja de loto tiene una superficie irregular y una histéresis de ángulo de contacto baja , lo que significa que la gota de agua no puede humedecer los espacios de la microestructura entre las puntas. Esto permite que el aire permanezca dentro de la textura, lo que genera una superficie heterogénea compuesta tanto de aire como de sólido. Como resultado, la fuerza adhesiva entre el agua y la superficie sólida es extremadamente baja, lo que permite que el agua se deslice fácilmente (es decir, fenómeno de " autolimpieza ").

Las micro y nanoestructuras de los pétalos de rosa son de mayor escala que las de las hojas de loto, lo que permite que la película líquida impregne la textura. Sin embargo, como se ve en la Figura 9, el líquido puede entrar en las ranuras de mayor escala, pero no en las ranuras más pequeñas. Esto se conoce como el régimen de humectación por impregnación de Cassie. Dado que el líquido puede humedecer las ranuras de mayor escala, la fuerza adhesiva entre el agua y el sólido es muy alta. Esto explica por qué la gota de agua no se caerá incluso si el pétalo se inclina en un ángulo o se da vuelta. Este efecto fallará si la gota tiene un volumen mayor a 10 μL porque se supera el equilibrio entre el peso y la tensión superficial. ^[42]

Transición de Cassie–Baxter a Wenzel

Figura 10: Estado de hongo

En el modelo Cassie-Baxter , la gota se asienta sobre la superficie texturizada con aire atrapado debajo. Durante la transición de humectación del estado Cassie al estado Wenzel, las bolsas de aire ya no son termodinámicamente estables y el líquido comienza a nuclearse desde el centro de la gota, creando un "estado de hongo", como se ve en la Figura 10. ^[43] La condición de penetración está dada por:

${\displaystyle \cos \,\left(\theta _{\text{C}}\right)={\frac {\phi -1}{r-\phi }}}$

dónde

• θ _C es el ángulo de contacto crítico
• Φ es la fracción de la interfaz sólido/líquido donde la gota está en contacto con la superficie
• r es la rugosidad del sólido (para una superficie plana, r = 1)

Figura 11: El frente de penetración se extiende más allá de la caída

El frente de penetración se propaga para minimizar la energía superficial hasta alcanzar los bordes de la gota, llegando así al estado de Wenzel. Dado que el sólido puede considerarse un material absorbente debido a su rugosidad superficial, este fenómeno de propagación e imbibición se denomina hemiwicking. Los ángulos de contacto en los que se produce la propagación/imbibición están entre 0 y π/2. ^[44]

El modelo de Wenzel es válido entre θ _C y π/2. Si el ángulo de contacto es menor que Θ _C , el frente de penetración se extiende más allá de la gota y se forma una película líquida sobre la superficie. La figura 11 muestra la transición del estado de Wenzel al estado de película superficial. La película suaviza la rugosidad de la superficie y el modelo de Wenzel ya no se aplica. En este estado, la condición de equilibrio y la relación de Young dan como resultado:

${\displaystyle \cos \,\left(\theta ^{*}\right)=\phi \cos \,\left(\theta _{C}\right)+\left(1-\phi \right)}$^[43]

Mediante el ajuste fino de la rugosidad de la superficie, es posible lograr una transición entre las regiones superhidrofóbicas y superhidrofílicas. En general, cuanto más rugosa es la superficie, más hidrofóbica es.

Dinámica de propagación

Si se coloca una gota sobre una superficie lisa y horizontal, generalmente no se encuentra en estado de equilibrio. Por lo tanto, se esparce hasta alcanzar un radio de contacto de equilibrio (humectación parcial). Si se tienen en cuenta las contribuciones capilares, gravitacionales y viscosas, el radio de la gota en función del tiempo se puede expresar como ^[45]

${\displaystyle r(t)=r_{e}\left[1-\exp \left(-\left({\frac {2\gamma _{LG}}{r_{e}^{12}}}+{\frac {\rho g}{9r_{e}^{10}}}\right){\frac {24\lambda V^{4}\left(t+t_{0}\right)}{\pi ^{2}\eta }}\right)\right]^{\frac {1}{6}}.}$

Para la situación de humectación completa, el radio de gota en cualquier momento durante el proceso de esparcimiento viene dado por

${\displaystyle r(t)=\left[\left(\gamma _{LG}{\frac {96\lambda V^{4}}{\pi ^{2}\eta }}\left(t+t_{0}\right)\right)^{\frac {1}{2}}+\left({\frac {\lambda (t+t_{0})}{\eta }}\right)^{\frac {2}{3}}{\frac {24\rho gV^{\frac {3}{8}}}{7\cdot 96^{\frac {1}{3}}\pi ^{\frac {4}{3}}\gamma _{LG}^{\frac {1}{3}}}}\right]^{\frac {1}{6}},}$

dónde

• γ _LG es la tensión superficial del fluido
• V es el volumen de la gota
• η es la viscosidad del fluido
• ρ es la densidad del fluido
• g es constante gravitacional
• λ es el factor de forma, 37,1  m ⁻¹
• t ₀ es el tiempo de retardo experimental
• r _e es el radio de caída en equilibrio

Modificación de las propiedades humectantes

Surfactantes

Muchos procesos tecnológicos requieren el control de la propagación de líquidos sobre superficies sólidas. Cuando se coloca una gota sobre una superficie, puede humedecerla completamente, parcialmente o no humedecerla. Al reducir la tensión superficial con surfactantes , se puede hacer que un material no humectante se vuelva parcial o completamente humectante. La energía libre excedente (σ) de una gota sobre una superficie sólida es: ^[46]

${\displaystyle \sigma =\gamma S+PV+\pi \,R^{2}\left(\gamma _{\text{SL}}-\gamma _{\text{SV}}\right)}$

• γ es la tensión interfacial líquido-vapor
• γ _SL es la tensión interfacial sólido-líquido
• γ _SV es la tensión interfacial sólido-vapor
• S es el área de la interfaz líquido-vapor
• P es el exceso de presión dentro del líquido.
• R es el radio de la base de la gota

Según esta ecuación, el exceso de energía libre se minimiza cuando γ disminuye, γ _SL disminuye o γ _SV aumenta. Los surfactantes se absorben en las interfaces líquido-vapor, sólido-líquido y sólido-vapor, que modifican el comportamiento de humectación de los materiales hidrofóbicos para reducir la energía libre. Cuando los surfactantes se absorben en una superficie hidrofóbica, los grupos de cabeza polar se orientan hacia la solución con la cola apuntando hacia afuera. En superficies más hidrofóbicas, los surfactantes pueden formar una bicapa en el sólido, lo que hace que se vuelva más hidrofílico. El radio dinámico de la gota se puede caracterizar a medida que la gota comienza a extenderse. Por lo tanto, el ángulo de contacto cambia según la siguiente ecuación: ^[46]

${\displaystyle \cos \,\left(\theta (t)\right)=\cos \,\left(\theta _{0}\right)+\left(\cos \,\left(\theta _{\infty }\right)-\cos \,\left(\theta _{0}\right)\right)\left(1-\mathrm {e} ^{-{\frac {t}{\tau }}}\right)}$

• θ ₀ es el ángulo de contacto inicial
• θ _∞ es el ángulo de contacto final
• τ es la escala de tiempo de transferencia de surfactante

A medida que se absorben los surfactantes, la tensión superficial sólido-vapor aumenta y los bordes de la gota se vuelven hidrófilos. Como resultado, la gota se expande.

Cambios en la superficie

Las hebras de un polímero sustituido con ferroceno sin carga se unen a una superficie de sílice hidrófoba . La oxidación de los grupos ferrocenilo produce una superficie hidrófila debido a las atracciones electrostáticas entre las cargas resultantes y el disolvente polar. ^[47]

El ferroceno es un compuesto organometálico redox -activo ^[48] que se puede incorporar en varios monómeros y utilizar para fabricar polímeros que se pueden unir a una superficie. ^[47] El vinilferroceno (ferrocenileteno) se puede preparar mediante una reacción de Wittig ^[49] y luego polimerizar para formar polivinilferroceno (PVFc), un análogo del poliestireno . Otro polímero que se puede formar es el poli( ferrocencarboxilato de 2-(metacriloiloxi)etilo ), PFcMA. Tanto el PVFc como el PFcMA se han unido a obleas de sílice y se ha medido la humectabilidad cuando las cadenas de polímero no están cargadas y cuando las fracciones de ferroceno se oxidan para producir grupos con carga positiva, como se ilustra a la derecha. ^[47] El ángulo de contacto con el agua en las obleas revestidas con PFcMA fue 70° menor después de la oxidación, mientras que en el caso de PVFc la disminución fue de 30°, y se ha demostrado que el cambio de humectabilidad es reversible. En el caso de PFcMA, se ha investigado el efecto de cadenas más largas con más grupos ferroceno (y también mayor masa molar ), y se encontró que las cadenas más largas producen reducciones del ángulo de contacto significativamente mayores. ^{[47] [50]}

Vacantes de oxígeno

Los óxidos de tierras raras exhiben hidrofobicidad intrínseca y, por lo tanto, se pueden utilizar en intercambiadores de calor térmicamente estables y otras aplicaciones que involucran hidrofobicidad a alta temperatura. ^[51] La presencia de vacantes de oxígeno en superficies de ceria u otros óxidos de tierras raras es fundamental para controlar la humectabilidad de la superficie. La adsorción de agua en superficies de óxido puede ocurrir como adsorción molecular, en la que las moléculas de H ₂ O permanecen intactas en la superficie terminada, o como adsorción disociativa , en la que OH y H se adsorben por separado ^[52] en superficies sólidas. Se encuentra generalmente que la presencia de vacantes de oxígeno mejora la hidrofobicidad al tiempo que promueve la adsorción disociativa. ^[53]

Véase también

• Adsorción  – Fenómeno de adhesión superficial
• Prueba de Amott
• Antivaho  : productos químicos que evitan la condensación del agua en forma de pequeñas gotas sobre una superficie.
• Deshumectación  : Retracción de un fluido de una superficie que estaba obligado a cubrir.
• Electrohumectación
• Flotación  : Fuerza ascendente que se opone al peso de un objeto sumergido en un fluido.Pages displaying short descriptions of redirect targets
• Técnica de la gota sésil  : método para determinar la energía superficial de un sólido
• Burbuja de jabón  : película fina de agua jabonosa que encierra aire.
• Aumento del core  – Técnica de laboratorio
• Corriente de humectación  : corriente eléctrica mínima a través de un contacto para atravesar la resistencia de la película superficial.
• Voltaje de humectación  : Corriente eléctrica mínima a través de un contacto para atravesar la resistencia de la película superficial.Pages displaying short descriptions of redirect targets
• Índice de humectabilidad de Lak
• Índice de humectabilidad USBM

Referencias

1. Carroll, Gregory T.; Turro, Nicholas J.; Mammana, Angela; Koberstein, Jeffrey T. (2017). "Inmovilización fotoquímica de polímeros sobre una superficie: control del espesor de la película y la humectabilidad". Fotoquímica y fotobiología . 93 (5): 1165–1169. doi :10.1111/php.12751. ISSN  0031-8655. PMID  28295380.
2. Dezellus, O.; Eustathopoulos, N. (2010). "Cuestiones fundamentales de la humectación reactiva por metales líquidos" (PDF) . Revista de Ciencia de Materiales . 45 (16): 4256–4264. Código Bibliográfico :2010JMatS..45.4256D. doi :10.1007/s10853-009-4128-x. S2CID  4512480.
3. Hu, Han; Ji, Hai-Feng; Sun, Ying (2013). "El efecto de las vacantes de oxígeno en la humectabilidad del agua de una superficie de ZnO". Química física Química Física . 15 (39): 16557–65. Bibcode :2013PCCP...1516557H. doi :10.1039/C3CP51848E. PMID  23949186. S2CID  205850095.
4. Amziane, Sofiane; Collet, Florence (5 de marzo de 2017). Materiales de construcción a base de bioagregados: informe de última generación del Comité Técnico 236-BBM de RILEM. Springer. ISBN 9789402410310.
5. Rafiee, J.; Mezcla.; Gullapalli, H.; Thomas, AV; Yavari, F.; Shi, Y.; Ajayan, PM; Koratkar, NA (2012). "Mojando la transparencia del grafeno" (PDF) . Materiales de la naturaleza . 11 (3): 217–22. Código Bib : 2012NatMa..11..217R. doi :10.1038/nmat3228. PMID  22266468. Archivado desde el original (PDF) el 15 de noviembre de 2017.
6. Mertens, Stijn FL; Hemmi, Adrian; Muff, Stefan; Gröning, Oliver; De Feyter, Steven; Osterwalder, Jürg; Greber, Thomas (2016). "Conmutación de la fricción estática y la adhesión de un líquido sobre un sólido" (PDF) . Nature . 534 (7609): 676–679. Bibcode :2016Natur.534..676M. doi :10.1038/nature18275. PMID  27357755. S2CID  205249367. Archivado desde el original (PDF) el 2019-04-11.
7. Sharfrin, E.; Zisman, William A. (1960). "Relaciones constitutivas en la humectación de superficies de baja energía y la teoría del método de retracción para preparar monocapas". The Journal of Physical Chemistry . 64 (5): 519–524. doi :10.1021/j100834a002.
8. Mantanis, GI; Young, RA (1997). "Mojado de la madera". Ciencia y tecnología de la madera . 31 (5): 339–353. doi :10.1007/BF01159153. ISSN  0043-7719.
9. Eustathopoulos, N.; Nicholas, MG; Drevet B. (1999). Mojabilidad a altas temperaturas . Oxford, Reino Unido: Pergamon. ISBN 978-0-08-042146-9.
10. Schrader, ME; Loeb, GI (1992). Enfoques modernos de la mojabilidad. Teoría y aplicaciones . Nueva York: Plenum Press. ISBN 978-0-306-43985-8.
11. de Gennes, PG (1985). "Mojadura: estática y dinámica" (PDF) . Reviews of Modern Physics . 57 (3): 827–863. Bibcode :1985RvMP...57..827D. doi :10.1103/RevModPhys.57.827. Archivado desde el original (PDF) el 2016-09-10.
12. Chen, Kuang-Yen; Ivashenko, Oleksii; Carroll, Gregory T.; Robertus, Jort; Kistemaker, Jos CM; London, Gábor; Browne, Wesley R.; Rudolf, Petra; Feringa, Ben L. (2014). "Control de la humectabilidad de la superficie mediante motores moleculares activados por luz tripodal". Revista de la Sociedad Química Americana . 136 (8): 3219–3224. doi :10.1021/ja412110t. PMID  24490770. S2CID  207106544.
13. Johnson, Rulon E. (1993) en Wettability Ed. Berg, John. C. Nueva York, NY: Marcel Dekker, Inc. ISBN 0-8247-9046-4 
14. Rowlinson, JS; Widom, B. (1982). Teoría molecular de la capilaridad . Oxford, Reino Unido: Clarendon Press. ISBN 978-0-19-855642-8.
15. Young, T. (1805). "Un ensayo sobre la cohesión de fluidos" (PDF) . Philosophical Transactions of the Royal Society of London . 95 : 65–87. doi :10.1098/rstl.1805.0005. S2CID  116124581.
16. TS Chow (1998). "Mojado de superficies rugosas". Journal of Physics: Condensed Matter . 10 (27): L445–L451. Código Bibliográfico :1998JPCM...10L.445C. doi :10.1088/0953-8984/10/27/001. S2CID  250874015.
17. Tadmor, Rafael (2004). "Energía lineal y relación entre los ángulos de avance, retroceso y contacto de Young". Langmuir . 20 (18): 7659–64. doi :10.1021/la049410h. PMID  15323516.
18. Schrader, Malcolm E. (1995). "Young-Dupre revisitado". Langmuir . 11 (9): 3585–3589. doi :10.1021/la00009a049.
19. Athanase M. Dupré, Paul Dupré (1 de enero de 1869). Théorie mécanique de la chaleur (en francés). Gauthier-Villars.
20. Clegg, Carl (2016). "Contact Angle Spreading Coefficient" (Coeficiente de dispersión del ángulo de contacto). www.ramehart.com . ramé-hart . Consultado el 6 de enero de 2016 .
21. Gibbs, Josiah Willard Autor del texto (1928). Obras completas / de JW Gibbs,...
22. Wciślik, Sylwia; Mukherjee, Sayantan (junio de 2022). "Evaluación de tres métodos de medición del ángulo de contacto estático para gotas de nanofluidos de TiO 2 durante la evaporación". Física de fluidos . 34 (6): 062006. Bibcode :2022PhFl...34f2006W. doi : 10.1063/5.0096644 . ISSN  1070-6631. S2CID  249715372.
23. Marmur, Abraham (febrero de 1997). "Tensión lineal y ángulo de contacto intrínseco en sistemas sólido-líquido-fluido". Journal of Colloid and Interface Science . 186 (2): 462–466. Bibcode :1997JCIS..186..462M. doi :10.1006/jcis.1996.4666. PMID  9056376.
24. Tadmor, Rafael (1 de agosto de 2004). "Energía lineal y relación entre ángulos de contacto de avance, retroceso y Young". Langmuir . 20 (18): 7659–7664. doi :10.1021/la049410h. ISSN  0743-7463. PMID  15323516.
25. Jasper, Warren J.; Rasipuram, Srinivasan (diciembre de 2017). "Relación entre el ángulo de contacto y el radio de la línea de contacto para gotas de aceite de tamaño micro a atto [10−6 a 10−18] litros". Journal of Molecular Liquids . 248 : 920–926. doi :10.1016/j.molliq.2017.10.134.
26. Jasper, Warren J.; Anand, Nadish (mayo de 2019). "Un enfoque variacional generalizado para predecir los ángulos de contacto de nanogotas sésiles en superficies planas y curvas". Journal of Molecular Liquids . 281 : 196–203. doi :10.1016/j.molliq.2019.02.039. S2CID  104412970.
27. Sun, Xuegui (2017). "Simulación de dinámica molecular de comportamientos de humectación de Li sobre superficies W". Ingeniería de fusión y diseño . 117 : 188–193. doi :10.1016/j.fusengdes.2016.06.037.
28. Costa, D (2017). "Efectos de humectación de bordes de soportes de γ-Al2O3 y anatasa-TiO2 por fases activas de MoS2 y CoMoS: un estudio DFT". Journal of Catalysis . 246 (2): 325–334. doi :10.1016/j.jcat.2006.12.007.
29. Hidrofobicidad de planos de CeO2 de bajo índice, Applied Surface Science, Elsevier, 2019, 478, pp.68-74. en Archivos abiertos de HAL
30. Robert J. Good (1992). "Ángulo de contacto, humectación y adhesión: una revisión crítica". Revista de ciencia y tecnología de la adhesión . 6 (12): 1269–1302. doi :10.1163/156856192X00629.
31. Shi, Z.; et al. (2018). "Histéresis dinámica del ángulo de contacto en puentes líquidos". Coloides y superficies A. 555 : 365–371. arXiv : 1712.04703 . doi :10.1016/j.colsurfa.2018.07.004. S2CID  51916594.
32. De Gennes, PG (1994). Interfaces blandas . Cambridge, Reino Unido: Cambridge University Press. ISBN 978-0-521-56417-5.
33. Abraham Marmur (2003). "Mojado de superficies rugosas hidrófobas: ser heterogéneo o no serlo". Langmuir . 19 (20): 8343–8348. doi :10.1021/la0344682.
34. Chen, Xuemei; Ma, Ruiyuan; Li, Jintao; Hao, Chonglei; Guo, Wei; Luk, BL; Li, Shuai Cheng; Yao, Shuhuai; Wang, Zuankai (2012). "Evaporación de gotas en superficies superhidrofóbicas: efectos de la rugosidad de la superficie y del tamaño de las gotas pequeñas" (PDF) . Physical Review Letters . 109 (11): 116101(1–6). Código Bibliográfico :2012PhRvL.109k6101C. doi :10.1103/PhysRevLett.109.116101. PMID  23005650. S2CID  29794436. Archivado desde el original (PDF) el 2019-04-11.
35. Wenzel, Robert N. "Resistencia de superficies sólidas a la humectación por agua". Química industrial y de ingeniería 28.8 (1936): 988-994.
36. de Gennes, Pierre-Gilles; Brochard-Wyart, Françoise; Quéré, David (2004). Fenómenos de capilaridad y humectación. Springer Nueva York. doi:10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8. S2CID 137894832
37. Whyman, G.; Bormashenko, Edward; Stein, Tamir (2008). "La derivación rigurosa de las ecuaciones de Young, Cassie–Baxter y Wenzel y el análisis del fenómeno de histéresis del ángulo de contacto". Chemical Physics Letters . 450 (4–6): 355–359. Bibcode :2008CPL...450..355W. doi :10.1016/j.cplett.2007.11.033.
38. Bormashenko, Edward (5 de agosto de 2009). "Ecuaciones de Young, Boruvka–Neumann, Wenzel y Cassie–Baxter como condiciones de transversalidad para el problema variacional de la humectación". Coloides y superficies A: aspectos fisicoquímicos y de ingeniería . 345 (1): 163–165. doi :10.1016/j.colsurfa.2009.04.054. ISSN  0927-7757.
39. Bormashenko, Edward (17 de enero de 2020). "Marco variacional para definir ángulos de contacto: un enfoque termodinámico general". Revista de ciencia y tecnología de adhesión . 34 (2): 219–230. doi :10.1080/01694243.2019.1663030. ISSN  0169-4243. S2CID  203537637.
40. Bormashenko, E. (2008). "¿Por qué se aplica la ecuación de Cassie-Baxter?". Colloids and Surfaces A. 324 ( 1–3): 47–50. doi :10.1016/j.colsurfa.2008.03.025.
41. Lin, F.; Zhang, Y; Xi, J; Zhu, Y; Wang, N; Xia, F; Jiang, L (2008). "Efecto pétalo: un estado superhidrofóbico con alta fuerza adhesiva". Langmuir . 24 (8): 4114–4119. doi :10.1021/la703821h. PMID  18312016.
42. Muzammil, I.; Li, YP; Li, XY; Lei, MK (2018). "Estructura química dependiente del ciclo de trabajo y humectabilidad de copolímeros de plasma pulsado por RF de ácido acrílico y octafluorociclobutano". Applied Surface Science . 436 : 411–418. Bibcode :2018ApSS..436..411M. doi :10.1016/j.apsusc.2017.11.261.
43. Ishino, C.; Okumura, K (2008). "Transiciones de humectación en superficies hidrófilas texturizadas" (PDF) . European Physical Journal . 25 (4): 415–424. Bibcode :2008EPJE...25..415I. doi :10.1140/epje/i2007-10308-y. PMID  18431542. S2CID  35973585. Archivado desde el original (PDF) el 2019-04-11.
44. Quere, D.; Thiele, Uwe; Quéré, David (2008). "Wetting of Textured Surfaces" (PDF) . Colloids and Surfaces A . 206 (1–3): 41–46. doi :10.1016/S0927-7757(02)00061-4. Archivado desde el original (PDF) el 2012-05-27 . Consultado el 2011-12-17 .
45. Härth, Michael; Schubert, Dirk W. (2012). "Enfoque simple para la dinámica de propagación de fluidos poliméricos". Química y física macromolecular . 213 (6): 654–665. doi :10.1002/macp.201100631.
46. Lee, KS; Ivanova, N.; Starov, VM; Hilal, N.; Dutschk, V. (2008). "Cinética de humectación y esparcimiento mediante soluciones acuosas de surfactantes". Avances en la ciencia de coloides e interfases . 144 (1–2): 54–65. doi :10.1016/j.cis.2008.08.005. PMID  18834966.
47. Pietschnig, R. (2016). "Polímeros con ferrocenos colgantes". Chemical Society Reviews . 45 (19): 5216–5231. doi : 10.1039/C6CS00196C . PMID  27156979.
48. Connelly, NG; Geiger, WE (1996). "Agentes redox químicos para la química organometálica" (PDF) . Chemical Reviews . 96 (2): 877–910. doi :10.1021/cr940053x. PMID  11848774. Archivado desde el original (PDF) el 22 de enero de 2016.
49. Liu, W.-Y.; Xu, Q.-H.; Ma, Y.-X.; Liang, Y.-M.; Dong, N.-L.; Guan, D.-P. (2001). "Síntesis sin disolventes de derivados de ferrocenileteno". Journal of Organometallic Chemistry . 625 : 128–132. doi :10.1016/S0022-328X(00)00927-X.
50. Elbert, J.; Gallei, M.; Rüttiger, C.; Brunsen, A.; Didzoleit, H.; Stühn, B.; Rehahn, M. (2013). "Polímeros de ferroceno para humectabilidad de superficie conmutable". Organometallics . 32 (20): 5873–5878. doi :10.1021/om400468p.
51. Kemsley, Jyllian (28 de enero de 2013). "Los óxidos de tierras raras son naturalmente hidrófobos". Chemical & Engineering News . 91 (4).
52. Fronzi, Marco; Assadi, M. Hussein N.; Hanaor, Dorian AH; Hanaor, Dorian AH; Gan, Yixiang (2019). "Conocimientos teóricos sobre la hidrofobicidad de superficies de CeO ₂ de bajo índice ". Ciencia de superficies aplicada . 478 : 68–74. arXiv : 1902.02662 . Código Bib : 2019ApSS..478...68F. doi :10.1016/j.apsusc.2019.01.208. S2CID  118895100.
53. Saini, CP; Barman, A.; Das, D.; Satpati, B.; Bhattacharyya, SR; Kanjilal, D.; Ponomaryov, A.; Zvyagin, S.; Kanjilal, A. (2017). "El papel de la vacancia de oxígeno en el comportamiento hidrofóbico de las nanobarras de TiO ₂ en pirámides de Si grabadas químicamente". The Journal of Physical Chemistry C . 121 : 278–283. doi :10.1021/acs.jpcc.6b08991.

Lectura adicional

• de Gennes, Pierre-Gilles; Brochard-Wyart, Françoise; Quéré, David (2004). Fenómenos de capilaridad y humectación . Springer Nueva York. doi :10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8. Número de identificación del sujeto  137894832.
• Victor M. Starov; Manuel G. Velarde ; Clayton J. Radke (2 de abril de 2007). Dinámica de humectación y propagación. CRC Press. ISBN 978-1-4200-1617-8.

Enlaces externos

• ¿Qué es la mojabilidad?
• Medios relacionados con la humectación en Wikimedia Commons