Dinámica de vuelo de naves espaciales

Aplicación de la dinámica mecánica para modelar el vuelo de vehículos espaciales

Trayectoria de vuelo de la misión de aterrizaje tripulado del Apolo 11 en la Luna, julio de 1969

La dinámica de vuelo de naves espaciales es la aplicación de la dinámica mecánica para modelar cómo las fuerzas externas que actúan sobre un vehículo o nave espacial determinan su trayectoria de vuelo. Estas fuerzas son principalmente de tres tipos: fuerza propulsora proporcionada por los motores del vehículo; fuerza gravitacional ejercida por la Tierra y otros cuerpos celestes; y sustentación y resistencia aerodinámicas (cuando se vuela en la atmósfera de la Tierra o de otro cuerpo, como Marte o Venus).

Los principios de la dinámica de vuelo se utilizan para modelar el vuelo propulsado de un vehículo durante el lanzamiento desde la Tierra; el vuelo orbital de una nave espacial; las maniobras para cambiar de órbita; el vuelo translunar e interplanetario; el lanzamiento y aterrizaje en un cuerpo celeste, con o sin atmósfera; la entrada a través de la atmósfera de la Tierra u otro cuerpo celeste; y el control de actitud . Por lo general, se programan en los sistemas de navegación inercial de un vehículo y son monitoreados en tierra por un miembro del equipo de controladores de vuelo conocido en la NASA como el oficial de dinámica de vuelo , o en la Agencia Espacial Europea como el navegante de la nave espacial.

La dinámica de vuelo depende de las disciplinas de propulsión, aerodinámica y astrodinámica ( mecánica orbital y mecánica celeste ). No se puede reducir simplemente al control de actitud; las naves espaciales reales no tienen volantes ni timones como los aviones o los barcos. A diferencia de la forma en que se representan las naves espaciales ficticias, una nave espacial en realidad no se inclina para girar en el espacio exterior, donde su trayectoria de vuelo depende estrictamente de las fuerzas gravitacionales que actúan sobre ella y de las maniobras de propulsión aplicadas.

Principios básicos

El vuelo de un vehículo espacial se determina mediante la aplicación de la segunda ley de movimiento de Newton : donde F es la suma vectorial de todas las fuerzas ejercidas sobre el vehículo, m es su masa actual y a es el vector de aceleración, la tasa instantánea de cambio de velocidad ( v ), que a su vez es la tasa instantánea de cambio de desplazamiento. Al despejar a , la aceleración es igual a la suma de fuerzas dividida por la masa. La aceleración se integra en el tiempo para obtener la velocidad, y la velocidad a su vez se integra para obtener la posición. $${\displaystyle \mathbf {F} =m\mathbf {a} ,}$$

Los cálculos de la dinámica de vuelo son manejados por sistemas de guía computarizados a bordo del vehículo; el estado de la dinámica de vuelo es monitoreado en tierra durante las maniobras motorizadas por un miembro del equipo de controlador de vuelo conocido en el Centro de Vuelos Espaciales Humanos de la NASA como el oficial de dinámica de vuelo , o en la Agencia Espacial Europea como el navegador de la nave espacial. ^[1]

En el caso de los vuelos atmosféricos con motor, las tres fuerzas principales que actúan sobre un vehículo son la fuerza de propulsión , la fuerza aerodinámica y la gravedad . Otras fuerzas externas, como la fuerza centrífuga , la fuerza de Coriolis y la presión de la radiación solar , son generalmente insignificantes debido al tiempo relativamente corto del vuelo con motor y al pequeño tamaño de la nave espacial, y pueden ignorarse en los cálculos simplificados de rendimiento. ^[2]

Propulsión

El empuje de un motor de cohete , en el caso general de operación en una atmósfera, se aproxima por: ^[3]

$${\displaystyle F={\dot {m}}\;v_{e}={\dot {m}}\;v_{\text{e-opt}}+A_{e}(p_{e}-p_{\text{amb}})}$$dónde,

• ${\displaystyle {\dot {m}}}$es el flujo másico de gases de escape
• ${\displaystyle v_{e}}$es la velocidad de escape efectiva (a veces también indicada como c en las publicaciones)
• ${\displaystyle v_{\text{e-opt}}}$es la velocidad efectiva del chorro cuando p _amb = p _e
• ${\displaystyle A_{e}}$es el área de flujo en el plano de salida de la boquilla (o el plano donde el chorro sale de la boquilla si hay flujo separado)
• ${\displaystyle p_{e}}$es la presión estática en el plano de salida de la boquilla
• ${\displaystyle p_{\text{amb}}}$es la presión ambiental (o atmosférica)

La velocidad de escape efectiva del propulsor del cohete es proporcional al impulso específico de vacío y se ve afectada por la presión atmosférica: ^[4] $${\displaystyle v_{e}=g_{0}\left(I_{\text{sp-vac}}-{\frac {A_{e}\,p_{\text{amb}}}{\dot {m}}}\right)}$$

dónde:

• ${\displaystyle I_{\text{sp-vac}}}$tiene unidades de segundos
• ${\displaystyle g_{0}}$es la aceleración gravitacional en la superficie de la Tierra

El impulso específico relaciona la capacidad delta-v con la cantidad de propulsor consumido según la ecuación del cohete Tsiolkovsky : ^[5] donde: $${\displaystyle \Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}}$$

• ${\displaystyle m_{0}}$es la masa total inicial, incluido el propulsor, en kg (o lb)
• ${\displaystyle m_{1}}$es la masa total final en kg (o lb)
• ${\displaystyle v_{e}}$es la velocidad de escape efectiva en m/s (o ft/s)
• ${\displaystyle \Delta v}$es el delta-v en m/s (o ft/s)

Fuerza aerodinámica

Las fuerzas aerodinámicas presentes cerca de un cuerpo con una atmósfera significativa como la Tierra , Marte o Venus se analizan como: sustentación , definida como el componente de fuerza perpendicular a la dirección del vuelo (no necesariamente hacia arriba para equilibrar la gravedad, como en el caso de un avión); y resistencia , el componente paralelo a la dirección del vuelo y en dirección opuesta. La sustentación y la resistencia se modelan como los productos de un coeficiente por la presión dinámica que actúa sobre un área de referencia: ^[6] $${\displaystyle \mathbf {L} =C_{L}qA_{\text{ref}}}$$ $${\displaystyle \mathbf {D} =C_{D}qA_{\text{ref}}}$$

dónde:

• C _L es aproximadamente lineal con α , el ángulo de ataque entre el eje del vehículo y la dirección de vuelo (hasta un valor límite), y es 0 en α = 0 para un cuerpo axisimétrico;
• C _D varía con α ² ;
• C _L y C _D varían con el número de Reynolds y el número de Mach ;
• q , la presión dinámica, es igual a 1/2 ρv ² , donde ρ es la densidad atmosférica, modelada para la Tierra como una función de la altitud en la Atmósfera Estándar Internacional (utilizando una distribución de temperatura asumida, variación de presión hidrostática y la ley de los gases ideales ); y
• Una _referencia es un área característica del vehículo, como por ejemplo el área de la sección transversal en el diámetro máximo.

Gravitación

La fuerza gravitatoria que ejerce un cuerpo celeste sobre un vehículo espacial se modela tomando el cuerpo y el vehículo como masas puntuales; los cuerpos (Tierra, Luna, etc.) se simplifican como esferas; y la masa del vehículo es mucho menor que la masa del cuerpo, de modo que se puede despreciar su efecto sobre la aceleración gravitatoria. Por lo tanto, la fuerza gravitatoria se calcula mediante:

$${\displaystyle \mathbf {W} =m\cdot g}$$

dónde:

• ${\displaystyle W}$es la fuerza gravitacional (peso);
• ${\displaystyle m}$es la masa del vehículo espacial; y
• ${\displaystyle r}$es la distancia radial del vehículo al centro del planeta; y
• ${\displaystyle r_{0}}$es la distancia radial desde la superficie del planeta hasta su centro; y
• ${\displaystyle g_{0}}$es la aceleración gravitacional en la superficie del planeta
• g es la aceleración gravitacional en la altitud, que varía con el cuadrado inverso de la distancia radial al centro del planeta: ^[7] $${\displaystyle g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}}$$

Vuelo propulsado

Las ecuaciones de movimiento utilizadas para describir el vuelo propulsado de un vehículo durante el lanzamiento pueden ser tan complejas como seis grados de libertad para los cálculos en vuelo, o tan simples como dos grados de libertad para las estimaciones preliminares de rendimiento. Los cálculos en vuelo tendrán en cuenta factores de perturbación como la achatación de la Tierra y la distribución no uniforme de la masa; y las fuerzas gravitacionales de todos los cuerpos cercanos, incluyendo la Luna, el Sol y otros planetas. Las estimaciones preliminares pueden hacer algunas suposiciones simplificadoras: un planeta esférico y uniforme; el vehículo puede representarse como una masa puntual; la solución de la trayectoria de vuelo presenta un problema de dos cuerpos ; y la trayectoria de vuelo local se encuentra en un solo plano) con una pérdida de precisión razonablemente pequeña. ^[7]

Vectores de velocidad, posición y fuerza que actúan sobre un vehículo espacial durante el lanzamiento

El caso general de un lanzamiento desde la Tierra debe tener en cuenta el empuje del motor, las fuerzas aerodinámicas y la gravedad. La ecuación de aceleración se puede reducir de forma vectorial a escalar descomponiéndola en sus componentes de tasa de cambio temporal tangencial (velocidad ) y angular (ángulo de la trayectoria de vuelo en relación con la vertical local) en relación con la plataforma de lanzamiento. Las dos ecuaciones se convierten así en: ${\displaystyle v}$ ${\displaystyle \theta }$

$${\displaystyle {\begin{aligned}{\dot {v}}&={\frac {F\cos \alpha }{m}}-{\frac {D}{m}}-g\cos \theta \\{\dot {\theta }}&={\frac {F\sin \alpha }{mv}}+{\frac {L}{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\end{aligned}}}$$

dónde:

• F es el empuje del motor;
• α es el ángulo de ataque;
• m es la masa del vehículo;
• D es la resistencia aerodinámica del vehículo ;
• L es su sustentación aerodinámica ;
• r es la distancia radial al centro del planeta; y
• g es la aceleración gravitacional en la altitud.

La masa disminuye a medida que se consume el propulsor y se eliminan las etapas del cohete , los motores o los tanques (si corresponde).

Los valores fijos del planeta de v y θ en cualquier momento del vuelo se determinan entonces mediante la integración numérica de las dos ecuaciones de velocidad desde el tiempo cero (cuando tanto v como θ son 0): $${\displaystyle {\begin{aligned}v&=\int _{t_{0}}^{t}{\dot {v}}\,dt\\\theta &=\int _{t_{0}}^{t}{\dot {\theta }}\,dt\end{aligned}}}$$

El análisis de elementos finitos se puede utilizar para integrar las ecuaciones, dividiendo el vuelo en pequeños incrementos de tiempo.

En la mayoría de los vehículos de lanzamiento , se generan niveles relativamente pequeños de sustentación y se emplea un viraje por gravedad , que depende principalmente del tercer término de la ecuación de la velocidad angular. En el momento del despegue, cuando el ángulo y la velocidad son ambos cero, la ecuación de punto theta es matemáticamente indeterminada y no se puede evaluar hasta que la velocidad se vuelve distinta de cero poco después del despegue. Pero observe que en esta condición, la única fuerza que puede hacer que el vehículo se incline es el empuje del motor que actúa en un ángulo de ataque distinto de cero (primer término) y quizás una pequeña cantidad de sustentación (segundo término), hasta que se alcanza un ángulo de inclinación distinto de cero. En el viraje por gravedad, el cabeceo se inicia aplicando un ángulo de ataque creciente (por medio del empuje del motor con cardán ), seguido de una disminución gradual del ángulo de ataque durante el resto del vuelo. ^{[7] [8]}

Una vez que se conocen la velocidad y el ángulo de la trayectoria de vuelo, la altitud y la distancia de vuelo se calculan como: ^[7] ${\displaystyle h}$ ${\displaystyle s}$

Vectores de velocidad y fuerza que actúan sobre un vehículo espacial durante el descenso y aterrizaje propulsados

$${\displaystyle {\begin{aligned}h&=\int _{t_{0}}^{t}v\cos \theta \,dt\\r&=r_{0}+h\\s&=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt\end{aligned}}}$$

Los valores fijos del planeta de v y θ se convierten a valores fijos del espacio (inerciales) con las siguientes conversiones: ^[7] donde ω es la velocidad de rotación del planeta en radianes por segundo, φ es la latitud del sitio de lanzamiento y A _z es el ángulo acimutal de lanzamiento . $${\displaystyle v_{s}={\sqrt {v^{2}+2\omega rv\cos \varphi \sin \theta \sin A_{z}+(\omega r\cos \theta )^{2}}},}$$ $${\displaystyle \theta _{s}=\arccos \left({\frac {v\cos \theta }{v_{s}}}\right)}$$

Los valores finales de v _s , θ _s y r deben coincidir con los requisitos de la órbita de destino, tal como lo determina la mecánica orbital (consulte Vuelo orbital, más arriba), donde v _s final suele ser la velocidad de periapsis (o circular) requerida y θ _s final es de 90 grados. Un análisis de descenso propulsado utilizaría el mismo procedimiento, con condiciones de contorno inversas.

Vuelo orbital

La mecánica orbital se utiliza para calcular el vuelo en órbita alrededor de un cuerpo central. Para órbitas suficientemente altas (por lo general, al menos 190 kilómetros (100 millas náuticas) en el caso de la Tierra), se puede suponer que la fuerza aerodinámica es insignificante para misiones de duración relativamente corta (aunque puede estar presente una pequeña cantidad de resistencia que resulte en una disminución de la energía orbital en períodos de tiempo más largos). Cuando la masa del cuerpo central es mucho mayor que la nave espacial y otros cuerpos están suficientemente alejados, la solución de las trayectorias orbitales se puede tratar como un problema de dos cuerpos. ^[9]

Se puede demostrar que esto da como resultado una trayectoria idealmente cónica (círculo, elipse, parábola o hipérbola) ^[10] con el cuerpo central ubicado en un foco. Las trayectorias orbitales son círculos o elipses; la trayectoria parabólica representa el primer escape del vehículo del campo gravitatorio del cuerpo central. Las trayectorias hiperbólicas son trayectorias de escape con exceso de velocidad y se tratarán en el apartado Vuelo interplanetario más adelante.

Las órbitas elípticas se caracterizan por tres elementos. ^[9] El semieje mayor a es el promedio del radio en el apoápside y el periápside : $${\displaystyle a={\frac {r_{a}+r_{p}}{2}}}$$

La excentricidad e se puede calcular entonces para una elipse, conociendo los ábsides: $${\displaystyle e={\frac {r_{a}}{a}}-1}$$

El período de tiempo para una órbita completa depende únicamente del semieje mayor y es independiente de la excentricidad: ^[11] donde es el parámetro gravitacional estándar del cuerpo central. $${\displaystyle T=2\pi {\sqrt {\frac {a^{3}}{\mu }}}}$$ ${\displaystyle \mu }$

Los elementos orbitales angulares de una nave espacial que orbita alrededor de un cuerpo central, que definen la orientación de la órbita en relación con su plano de referencia fundamental.

La orientación de la órbita en el espacio está determinada por tres ángulos:

• La inclinación i , del plano orbital con el plano fundamental (este suele ser el plano ecuatorial de un planeta o una luna, o en el caso de una órbita solar, el plano orbital de la Tierra alrededor del Sol, conocido como eclíptica ). La inclinación positiva es hacia el norte, mientras que la inclinación negativa es hacia el sur.
• La longitud del nodo ascendente Ω, medida en el plano fundamental en sentido antihorario mirando hacia el sur, desde una dirección de referencia (normalmente el equinoccio de primavera ) hasta la línea donde la nave espacial cruza este plano de sur a norte. (Si la inclinación es cero, este ángulo no está definido y se toma como 0).
• El argumento del periapsis ω se mide en el plano orbital en sentido antihorario mirando hacia el sur, desde el nodo ascendente hasta el periapsis. Si la inclinación es 0, no hay nodo ascendente, por lo que ω se mide desde la dirección de referencia. Para una órbita circular, no hay periapsis, por lo que ω se toma como 0.

El plano orbital es idealmente constante, pero suele estar sujeto a pequeñas perturbaciones causadas por la achatación planetaria y la presencia de otros cuerpos.

La posición de la nave espacial en órbita está especificada por la anomalía verdadera, , un ángulo medido desde el periapsis, o para una órbita circular, desde el nodo ascendente o dirección de referencia. El semilato recto , o radio a 90 grados del periapsis, es: ^[12] ${\displaystyle \nu }$ $${\displaystyle p=a(1-e^{2})\,}$$

El radio en cualquier posición en vuelo es: y la velocidad en esa posición es: $${\displaystyle r={\frac {p}{1+e\cos \nu }}}$$ $${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}}$$

Tipos de órbita

Circular

Para una órbita circular, r _a = r _p = a y la excentricidad es 0. La velocidad circular en un radio dado es: $${\displaystyle v_{c}={\sqrt {\frac {\mu }{r}}}}$$

Elíptico

Para una órbita elíptica, e es mayor que 0 pero menor que 1. La velocidad del periapsis es: y la velocidad del apoapsis es: $${\displaystyle v_{p}={\sqrt {\frac {\mu (1+e)}{a(1-e)}}}}$$ $${\displaystyle v_{a}={\sqrt {\frac {\mu (1-e)}{a(1+e)}}}\,}$$

La condición límite es una órbita de escape parabólica , cuando e = 1 y r _a se vuelve infinita. La velocidad de escape en el periapsis es entonces $${\displaystyle v_{e}={\sqrt {\frac {2\mu }{r_{p}}}}}$$

Ángulo de trayectoria de vuelo

El momento angular específico de cualquier órbita cónica, h , es constante y es igual al producto del radio por la velocidad en el periapsis. En cualquier otro punto de la órbita, es igual a: ^[13] donde φ es el ángulo de la trayectoria de vuelo medido desde la horizontal local (perpendicular a  r ). Esto permite el cálculo de φ en cualquier punto de la órbita, conociendo el radio y la velocidad: $${\displaystyle h=rv\cos \varphi ,}$$ $${\displaystyle \varphi =\arccos \left({\frac {r_{p}v_{p}}{rv}}\right)}$$

Tenga en cuenta que el ángulo de la trayectoria de vuelo es una constante de 0 grados (90 grados desde la vertical local) para una órbita circular.

Anomalía verdadera en función del tiempo

Se puede demostrar que la ecuación del momento angular dada anteriormente también relaciona la tasa de cambio en la anomalía verdadera con r , v y φ , por lo tanto, la anomalía verdadera se puede encontrar como una función del tiempo desde el paso del periapsis por integración: ^[14] $${\displaystyle \nu =r_{p}v_{p}\int _{t_{p}}^{t}{\frac {1}{r^{2}}}\,dt}$$

Por el contrario, el tiempo necesario para alcanzar una anomalía dada es: $${\displaystyle t={\frac {1}{r_{p}v_{p}}}\int _{0}^{\nu }r^{2}\,d\nu }$$

Maniobras orbitales

Una vez en órbita, una nave espacial puede encender motores de cohetes para realizar cambios en el plano a una altitud o tipo de órbita diferente, o para cambiar su plano orbital. Estas maniobras requieren cambios en la velocidad de la nave, y la ecuación clásica de cohetes se utiliza para calcular los requisitos de propulsante para un delta-v dado . Un presupuesto de delta- v sumará todos los requisitos de propulsante, o determinará el delta-v total disponible a partir de una cantidad dada de propulsante, para la misión. La mayoría de las maniobras en órbita se pueden modelar como impulsivas , es decir, como un cambio casi instantáneo en la velocidad, con una pérdida mínima de precisión.

Cambios en el plano

Circularización de la órbita

Una órbita elíptica se convierte más fácilmente en una órbita circular en el periapsis o apoapsis aplicando una única quema de motor con un delta v igual a la diferencia entre la velocidad circular de la órbita deseada y la velocidad del periapsis o apoapsis de la órbita actual:

Para circularizar en el periapsis se realiza una quemadura retrógrada: $${\displaystyle \Delta v\ =v_{c}-v_{p}}$$

Para circularizar en apoapsis se realiza una quemadura posígrada: $${\displaystyle \Delta v\ =v_{c}-v_{a}}$$

Cambio de altitud por transferencia de Hohmann

Órbita de transferencia de Hohmann, 2, de una órbita (1) a una órbita superior (3)

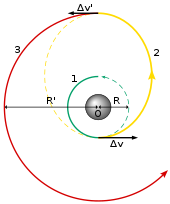
La órbita de transferencia de Hohmann es la maniobra más sencilla que se puede utilizar para mover una nave espacial de una altitud a otra. Se requieren dos arranques: el primero para enviar la nave a la órbita de transferencia elíptica y el segundo para circularizar la órbita objetivo.

Para elevar una órbita circular en , la primera quema posígrada eleva la velocidad a la velocidad del periapsis de la órbita de transferencia: La segunda quema posígrada, realizada en el apoapsis, eleva la velocidad a la velocidad de la órbita objetivo: ${\displaystyle v_{1}}$ $${\displaystyle \Delta v_{1}\ =v_{p}-v_{1}}$$ $${\displaystyle \Delta v_{2}\ =v_{2}-v_{a}}$$

La maniobra para bajar la órbita es la imagen especular de la maniobra de elevación; ambas quemaduras se realizan retrógradas.

Cambio de altitud por transferencia bielíptica

Una transferencia bielíptica desde una órbita inicial circular baja (azul oscuro) a una órbita circular más alta (roja)

Una maniobra de cambio de altitud ligeramente más complicada es la transferencia bielíptica , que consiste en dos órbitas semielípticas; la primera, de encendido positivo, envía la nave espacial a una apoápside arbitrariamente alta elegida en algún punto alejado del cuerpo central. En este punto, un segundo encendido modifica la periápside para que coincida con el radio de la órbita final deseada, donde se realiza un tercer encendido retrógrado para inyectar la nave espacial en la órbita deseada. ^[15] Si bien esto requiere un tiempo de transferencia más largo, una transferencia bielíptica puede requerir menos propulsor total que la transferencia de Hohmann cuando la relación entre los radios de la órbita inicial y la órbita objetivo es 12 o mayor. ^{[16] [17]} ${\displaystyle r_{b}}$

Quemadura 1 (posigrada): Quemadura 2 (posigrada o retrógrada), para hacer coincidir el periapsis con la altitud de la órbita objetivo: Quemadura 3 (retrógrada): $${\displaystyle \Delta v_{1}\ ={v_{p}}_{1}-v_{1}}$$ $${\displaystyle \Delta v_{2}\ ={v_{a}}_{2}-{v_{a}}_{1}}$$ $${\displaystyle \Delta v_{3}\ =v_{2}-{v_{p}}_{2}}$$

Cambio de avión

Las maniobras de cambio de plano se pueden realizar solas o en conjunción con otros ajustes de órbita. Para una maniobra de cambio de plano de rotación pura, que consiste únicamente en un cambio en la inclinación de la órbita, el momento angular específico, h , de las órbitas inicial y final son iguales en magnitud pero no en dirección. Por lo tanto, el cambio en el momento angular específico se puede escribir como: donde h es el momento angular específico antes del cambio de plano, y Δ i es el cambio deseado en el ángulo de inclinación. A partir de esto se puede demostrar ^[18] que el delta- v requerido es: $${\displaystyle \Delta h=2h\sin \left({\frac {|\Delta i|}{2}}\right)}$$ $${\displaystyle \Delta v={\frac {2h\sin {\frac {|\Delta i|}{2}}}{r}}}$$

A partir de la definición de h , esto también se puede escribir como: donde v es la magnitud de la velocidad antes del cambio de plano y φ es el ángulo de la trayectoria de vuelo. Usando la aproximación de ángulo pequeño , esto se convierte en: $${\displaystyle \Delta v=2v\cos \varphi \sin \left({\frac {\left|\Delta i\right|}{2}}\right)}$$ $${\displaystyle \Delta v=v\cos(\varphi )\left|\Delta i\right|}$$

El delta- v total para una maniobra combinada se puede calcular mediante una suma vectorial del delta- v de rotación pura y el delta- v del otro cambio orbital planificado.

Vuelo translunar

Una trayectoria translunar típica

Los vehículos enviados en misiones lunares o planetarias generalmente no se lanzan mediante inyección directa a la trayectoria de partida, sino que primero se colocan en una órbita de estacionamiento baja en la Tierra ; esto permite la flexibilidad de una ventana de lanzamiento más grande y más tiempo para verificar que el vehículo está en condiciones adecuadas para el vuelo.

La velocidad de escape no es necesaria para el vuelo a la Luna; más bien, el apogeo del vehículo se eleva lo suficiente como para que pase por un punto en el que entre en la esfera de influencia gravitatoria (IEG) de la Luna. Esta se define como la distancia desde un satélite a la que su atracción gravitatoria sobre una nave espacial es igual a la de su cuerpo central, que es donde D es la distancia media desde el satélite hasta el cuerpo central, y m _c y m _s son las masas del cuerpo central y del satélite, respectivamente. Este valor es de aproximadamente 66.300 kilómetros (35.800 millas náuticas) desde la Luna de la Tierra. ^[19] $${\displaystyle r_{\text{SOI}}=D\left({\frac {m_{s}}{m_{c}}}\right)^{2/5},}$$

Una solución precisa de la trayectoria requiere un tratamiento como un problema de tres cuerpos , pero se puede realizar una estimación preliminar utilizando una aproximación cónica parcheada de las órbitas alrededor de la Tierra y la Luna, parcheada en el punto SOI y teniendo en cuenta el hecho de que la Luna es un marco de referencia giratorio alrededor de la Tierra.

Inyección translunar

Esto debe cronometrarse de modo que la Luna esté en posición de capturar el vehículo, y podría modelarse en una primera aproximación como una transferencia de Hohmann. Sin embargo, la duración de la combustión del cohete suele ser lo suficientemente larga y ocurre durante un cambio suficiente en el ángulo de la trayectoria de vuelo, por lo que esto no es muy preciso. Debe modelarse como una maniobra no impulsiva , que requiere la integración mediante análisis de elementos finitos de las aceleraciones debidas al empuje propulsor y la gravedad para obtener la velocidad y el ángulo de la trayectoria de vuelo: ^[7] donde: $${\displaystyle {\begin{aligned}{\dot {v}}&={\frac {F\cos \alpha }{m}}-g\cos \theta \\{\dot {\theta }}&={\frac {F\sin \alpha }{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\\v&=\int _{t_{0}}^{t}{\dot {v}}\,dt\\\theta &=\int _{t_{0}}^{t}{\dot {\theta }}\,dt\end{aligned}}}$$

• F es el empuje del motor;
• α es el ángulo de ataque;
• m es la masa del vehículo;
• r es la distancia radial al centro del planeta; y
• g es la aceleración gravitacional , que varía con el cuadrado inverso de la distancia radial: ^[7] $${\displaystyle g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}}$$

La altitud , la distancia de alcance y la distancia radial desde el centro de la Tierra se calculan entonces como: ^[7] ${\displaystyle h}$ ${\displaystyle s}$ ${\displaystyle r}$ $${\displaystyle {\begin{aligned}h&=\int _{t_{0}}^{t}v\cos \theta \,dt\\r&=r_{0}+h\\s&=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt\end{aligned}}}$$

Correcciones a mitad de camino

Una trayectoria lunar simple se mantiene en un plano, lo que da como resultado un sobrevuelo o una órbita lunar dentro de un pequeño rango de inclinación con respecto al ecuador de la Luna. Esto también permite un "retorno libre", en el que la nave espacial regresaría a la posición adecuada para el reingreso a la atmósfera de la Tierra si no fuera inyectada en la órbita lunar. Por lo general, se requieren cambios de velocidad relativamente pequeños para corregir los errores de trayectoria. Este tipo de trayectoria se utilizó para las misiones lunares tripuladas Apolo 8 , Apolo 10 , Apolo 11 y Apolo 12 .

Se puede obtener una mayor flexibilidad en la cobertura de la órbita lunar o del lugar de aterrizaje (en mayores ángulos de inclinación lunar) realizando una maniobra de cambio de plano en pleno vuelo; sin embargo, esto elimina la opción de retorno libre, ya que el nuevo plano alejaría la trayectoria de retorno de emergencia de la nave espacial del punto de reentrada atmosférica de la Tierra y la dejaría en una órbita terrestre alta. Este tipo de trayectoria se utilizó en las últimas cinco misiones Apolo (13 a 17).

Inserción en órbita lunar

En el programa Apolo , la quema de inserción en órbita lunar retrógrada se realizó a una altitud de aproximadamente 110 kilómetros (59 millas náuticas) en el lado oculto de la Luna. Esto se convirtió en el pericintio de las órbitas iniciales, con un apocintio del orden de 300 kilómetros (160 millas náuticas). El delta v fue de aproximadamente 1000 metros por segundo (3300 pies/s). Dos órbitas más tarde, la órbita se circularizó a 110 kilómetros (59 millas náuticas). ^[20] Para cada misión, el oficial de dinámica de vuelo preparó 10 soluciones de inserción en órbita lunar para que se pudiera elegir la que tuviera el consumo de combustible óptimo (mínimo) y que cumpliera mejor con los requisitos de la misión; esto se cargó en la computadora de la nave espacial y tuvo que ser ejecutado y monitoreado por los astronautas en el lado oculto de la Luna, mientras estaban fuera de contacto por radio con la Tierra. ^[20]

Vuelo interplanetario

Para abandonar completamente el campo gravitatorio de un planeta para llegar a otro, es necesaria una trayectoria hiperbólica relativa al planeta de partida, con exceso de velocidad añadido a (o restado de) la velocidad orbital del planeta de partida alrededor del Sol. La órbita de transferencia heliocéntrica deseada a un planeta superior tendrá su perihelio en el planeta de partida, requiriendo que el exceso de velocidad hiperbólica se aplique en la dirección posígrada, cuando la nave espacial está lejos del Sol. A un destino planetario inferior , el afelio estará en el planeta de partida, y el exceso de velocidad se aplica en la dirección retrógrada cuando la nave espacial está hacia el Sol. Para cálculos precisos de la misión, los elementos orbitales de los planetas deben obtenerse de una efemérides , ^[21] como la publicada por el Laboratorio de Propulsión a Chorro de la NASA .

Simplificando suposiciones

A los efectos del análisis preliminar de la misión y los estudios de viabilidad, se pueden hacer ciertas suposiciones simplificadas para permitir el cálculo del delta-v con un error muy pequeño: ^[24]

• Las órbitas de todos los planetas, excepto Mercurio , tienen una excentricidad muy pequeña y, por lo tanto, se puede suponer que son circulares a una velocidad orbital y una distancia media constantes del Sol.
• Las órbitas de todos los planetas (excepto Mercurio) son casi coplanares, con una inclinación muy pequeña respecto a la eclíptica (3,39 grados o menos; la inclinación de Mercurio es de 7,00 grados).
• Los efectos perturbadores de la gravedad de los otros planetas son insignificantes.
• La nave espacial pasará la mayor parte de su tiempo de vuelo únicamente bajo la influencia gravitatoria del Sol, excepto breves períodos en los que estará en la esfera de influencia de los planetas de partida y destino.

Dado que las naves espaciales interplanetarias pasan un largo período de tiempo en órbita heliocéntrica entre los planetas, que se encuentran a distancias relativamente grandes entre sí, la aproximación cónica parcheada es mucho más precisa para las trayectorias interplanetarias que para las trayectorias translunares. ^[24] El punto de parche entre la trayectoria hiperbólica relativa al planeta de partida y la órbita de transferencia heliocéntrica se produce en el radio de la esfera de influencia del planeta en relación con el Sol, como se define anteriormente en Vuelo orbital. Dada la relación de masas del Sol de 333.432 veces la de la Tierra y una distancia de 149.500.000 kilómetros (80.700.000 millas náuticas), el radio de la esfera de influencia de la Tierra es de 924.000 kilómetros (499.000 millas náuticas) (aproximadamente 1.000.000 de kilómetros). ^[25]

Órbita de transferencia heliocéntrica

La órbita de transferencia necesaria para llevar la nave espacial desde la órbita del planeta de partida hasta el planeta de destino se elige entre varias opciones:

• Una órbita de transferencia Hohmann requiere la menor cantidad posible de propulsor y delta-v; esto es la mitad de una órbita elíptica con afelio y perihelio tangenciales a las órbitas de ambos planetas, con el tiempo de vuelo de ida más largo igual a la mitad del período de la elipse. Esto se conoce como una misión de clase conjunción . ^{[26] [27]} No hay una opción de "retorno libre", porque si la nave espacial no entra en órbita alrededor del planeta de destino y en su lugar completa la órbita de transferencia, el planeta de salida no estará en su posición original. Usar otra transferencia Hohmann para regresar requiere un tiempo de espera significativo en el planeta de destino, lo que resulta en un tiempo total de misión de ida y vuelta muy largo. ^[28] El escritor de ciencia ficción Arthur C. Clarke escribió en su libro de 1951 La exploración del espacio que un viaje de ida y vuelta de la Tierra a Marte requeriría 259 días de ida y otros 259 días de vuelta, con una estadía de 425 días en Marte.
• Aumentar la velocidad del ábside de salida (y por lo tanto el semieje mayor) da como resultado una trayectoria que cruza la órbita del planeta de destino de manera no tangencial antes de alcanzar el ábside opuesto, lo que aumenta delta-v pero reduce el tiempo de tránsito de salida por debajo del máximo. ^[28]
• Una maniobra de asistencia gravitacional , a veces conocida como "maniobra de honda" o misión Crocco en honor a su proponente en 1956 , Gaetano Crocco , da como resultado una misión de clase oposición con un tiempo de permanencia mucho más corto en el destino. ^{[29] [27]} Esto se logra al pasar junto a otro planeta, utilizando su gravedad para alterar la órbita. Un viaje de ida y vuelta a Marte, por ejemplo, se puede acortar significativamente de los 943 días necesarios para la misión de conjunción a menos de un año, al pasar junto a Venus al regresar a la Tierra.

Salida hiperbólica

La velocidad hiperbólica excedente requerida v _∞ (a veces llamada velocidad característica ) es la diferencia entre la velocidad de salida de la órbita de transferencia y la velocidad orbital heliocéntrica del planeta de salida. Una vez que se determina esto, la velocidad de inyección relativa al planeta de salida en el periapsis es: ^[30] $${\displaystyle v_{p}={\sqrt {{\frac {2\mu }{r_{p}}}+v_{\infty }^{2}}}\,}$$

El vector de velocidad en exceso de una hipérbola se desplaza de la tangente del periapsis en un ángulo característico, por lo tanto, la quemadura de inyección del periapsis debe adelantarse al punto de partida planetario en el mismo ángulo: ^[31] $${\displaystyle \delta =\arcsin {\frac {1}{e}}}$$

La ecuación geométrica de la excentricidad de una elipse no se puede utilizar para una hipérbola, pero la excentricidad se puede calcular a partir de formulaciones dinámicas como: ^[32] donde h es el momento angular específico, como se indicó anteriormente en la sección Vuelo orbital, calculado en el periapsis: ^[31] y ε es la energía específica: ^[31] $${\displaystyle e={\sqrt {1+{\frac {2\varepsilon h^{2}}{\mu ^{2}}}}},}$$ $${\displaystyle h=r_{p}v_{p},}$$ $${\displaystyle \varepsilon ={\frac {v^{2}}{2}}-{\frac {\mu }{r}}\,}$$

Además, las ecuaciones para r y v dadas en Vuelo orbital dependen del semieje mayor y, por lo tanto, no son utilizables para una trayectoria de escape. Pero establecer el radio en el periapsis igual a la ecuación r en anomalía cero da una expresión alternativa para el semilato recto: que da una ecuación más general para el radio en función de la anomalía que es utilizable en cualquier excentricidad: $${\displaystyle p=r_{p}(1+e),\,}$$ $${\displaystyle r={\frac {r_{p}(1+e)}{1+e\cos \nu }}\,}$$

Sustituir la expresión alternativa para p también da una expresión alternativa para a (que se define para una hipérbola, pero ya no representa el semieje mayor). Esto da una ecuación para la velocidad en función del radio que también se puede utilizar en cualquier excentricidad: $${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1-e^{2}}{r_{p}(1+e)}}\right)}}\,}$$

Las ecuaciones para el ángulo de la trayectoria de vuelo y la anomalía en función del tiempo dadas en el vuelo orbital también se pueden utilizar para trayectorias hiperbólicas.

Ventanas de lanzamiento

Existe una gran variación en el tiempo del cambio de velocidad necesario para una misión, debido a que las posiciones relativas de los planetas varían constantemente. Por lo tanto, las ventanas de lanzamiento óptimas a menudo se eligen a partir de los resultados de gráficos de porkchop que muestran contornos de energía característica ( v _∞ ² ) graficados en función del tiempo de salida y llegada.

Entrada atmosférica

El ingreso, descenso y aterrizaje controlados de un vehículo se logran eliminando el exceso de energía cinética mediante el calentamiento aerodinámico de la resistencia, lo que requiere algún medio de protección térmica y/o empuje retrógrado. El descenso terminal generalmente se logra mediante paracaídas y/o frenos de aire .

Control de actitud

Dado que las naves espaciales pasan la mayor parte de su tiempo de vuelo navegando sin propulsión por el vacío del espacio, se diferencian de las aeronaves en que su trayectoria de vuelo no está determinada por su actitud (orientación), excepto durante el vuelo atmosférico para controlar las fuerzas de sustentación y resistencia, y durante el vuelo propulsado para alinear el vector de empuje. No obstante, el control de actitud se mantiene a menudo en vuelo sin propulsión para mantener la nave espacial en una orientación fija con fines de observación astronómica , comunicaciones o generación de energía solar ; o para colocarla en un giro controlado para control térmico pasivo , o para crear gravedad artificial dentro de la nave.

El control de la actitud se mantiene con respecto a un marco de referencia inercial u otra entidad (la esfera celeste, ciertos campos, objetos cercanos, etc.). La actitud de una nave se describe mediante ángulos relativos a tres ejes de rotación mutuamente perpendiculares, denominados balanceo, cabeceo y guiñada. La orientación se puede determinar mediante calibración utilizando un sistema de guía externo, como la determinación de los ángulos con una estrella de referencia o el Sol, y luego se monitorea internamente utilizando un sistema inercial de giroscopios mecánicos u ópticos . La orientación es una cantidad vectorial descrita por tres ángulos para la dirección instantánea y las velocidades instantáneas de balanceo en los tres ejes de rotación. El aspecto del control implica tanto el conocimiento de la orientación instantánea y las velocidades de balanceo como la capacidad de cambiar las velocidades de balanceo para asumir una nueva orientación utilizando un sistema de control de reacción u otros medios.

La segunda ley de Newton, aplicada al movimiento rotacional en lugar del movimiento lineal, se convierte en: ^[33] donde es el par neto sobre un eje de rotación ejercido sobre el vehículo, I _x es su momento de inercia sobre ese eje (una propiedad física que combina la masa y su distribución alrededor del eje), y es la aceleración angular sobre ese eje en radianes por segundo por segundo. Por lo tanto, la tasa de aceleración en grados por segundo por segundo es $${\displaystyle {\boldsymbol {\tau }}_{x}=I_{x}{\boldsymbol {\alpha }}_{x},}$$ ${\displaystyle {\boldsymbol {\tau }}_{x}}$ ${\displaystyle \alpha _{x}}$ $${\displaystyle {\boldsymbol {\alpha }}_{x}={\tfrac {180}{\pi }}{\boldsymbol {\tau }}_{x}/I_{x},}$$

De manera análoga al movimiento lineal, la tasa de rotación angular (grados por segundo) se obtiene integrando α a lo largo del tiempo: y la rotación angular es la integral temporal de la tasa: ${\displaystyle {\boldsymbol {\omega }}_{x}}$ $${\displaystyle {\omega _{x}}=\int _{t_{0}}^{t}{\alpha _{x}}dt}$$ ${\displaystyle {\boldsymbol {\theta }}_{x}}$ $${\displaystyle \theta _{x}=\int _{t_{0}}^{t}{\omega _{x}}dt}$$

Los tres momentos principales de inercia I _x , I _y e I _z alrededor de los ejes de balanceo, cabeceo y guiñada, se determinan a través del centro de masa del vehículo .

El par de control para un vehículo de lanzamiento a veces se proporciona aerodinámicamente mediante aletas móviles, y generalmente montando los motores en cardanes para vectorizar el empuje alrededor del centro de masa. El par se aplica con frecuencia a las naves espaciales, operando sin fuerzas aerodinámicas, mediante un sistema de control de reacción , un conjunto de propulsores ubicados alrededor del vehículo. Los propulsores se encienden, ya sea manualmente o bajo control de guía automático, en ráfagas cortas para lograr la velocidad de rotación deseada, y luego se encienden en la dirección opuesta para detener la rotación en la posición deseada. El par alrededor de un eje específico es: donde r es su distancia desde el centro de masa y F es el empuje de un propulsor individual (solo se incluye el componente de F perpendicular a r ). $${\displaystyle {\boldsymbol {\tau }}=\sum _{i=1}^{N}(\mathbf {r} _{i}\times \mathbf {F} _{i}),}$$

Para situaciones en las que el consumo de combustible puede ser un problema (como satélites de larga duración o estaciones espaciales), se pueden utilizar medios alternativos para proporcionar el par de control, como ruedas de reacción ^[34] o giroscopios de momento de control . ^[35]

Notas

1. "ESA - Dinámica de vuelo". Agencia Espacial Europea . Consultado el 22 de junio de 2020 .
2. Bate, Mueller y White (1971), págs. 11-12.
3. George P. Sutton y Oscar Biblarz (2001). Elementos de propulsión de cohetes (7.ª ed.). Wiley Interscience. ISBN 0-471-32642-9.Véase la ecuación 2-14.
4. Sutton, George P.; Biblarz, Óscar (2001). Elementos de propulsión de cohetes. John Wiley e hijos. ISBN 978-0-471-32642-7Archivado desde el original el 12 de enero de 2014 . Consultado el 28 de mayo de 2016 .
5. George P. Sutton y Oscar Biblarz (2001). Elementos de propulsión de cohetes (7.ª ed.). Wiley Interscience. ISBN 0-471-32642-9.Véase la ecuación 3-33.
6. Anderson (2004), págs. 257–261.
7. Kromis (1967), pág. 11:154.
8. Glasstone (1965), pág. 209, §4.97.
9. Perry (1967), pág. 11:151.
10. Bate, Mueller y White (1971), págs. 11–40.
11. Bate, Mueller y White (1971), pág. 33.
12. Bate, Mueller y White (1971), pág. 24.
13. Bate, Mueller y White (1971), pág. 18.
14. Bate, Mueller y White (1971), págs. 31-32.
15. Curtis, Howard (2005). Mecánica orbital para estudiantes de ingeniería. Elsevier . p. 264. ISBN 0-7506-6169-0.
16. Gobetz, FW; Doll, JR (mayo de 1969). "Un estudio de trayectorias impulsivas". Revista AIAA . 7 (5). Instituto Americano de Aeronáutica y Astronáutica : 801–834. Bibcode :1969AIAAJ...7..801D. doi :10.2514/3.5231.
17. Escobal, Pedro R. (1968). Métodos de Astrodinámica . Nueva York: John Wiley & Sons . ISBN 978-0-471-24528-5.
18. Hintz (2015), pág. 112.
19. Bate, Mueller y White (1971), págs. 333–334.
20. O'Brien, Frank (1999). "Inserción en la órbita lunar". Diario del vuelo Apollo . David Woods . Consultado el 25 de junio de 2020 .
21. Bate, Mueller y White (1971), pág. 359.
22. "Elementos keplerianos de 1800 d. C. a 2050 d. C." JPL Solar System Dynamics. Archivado desde el original el 23 de julio de 2009. Consultado el 17 de diciembre de 2009 .
23. Bate, Mueller y White (1971), pág. 361.
24. Bate, Mueller y White (1971), págs. 359, 362.
25. Bate, Mueller y White (1971), pág. 368.
26. Mattfeld y col. (2015), pág. 3.
27. Drake y otros, 2017.
28. Bate, Mueller y White (1971), págs. 362–363.
29. Mattfeld y col. (2015), págs. 3–4.
30. Bate, Mueller y White (1971), pág. 369.
31. Bate, Mueller y White (1971), pág. 371.
32. Bate, Mueller y White (1971), pág. 372.
33. Beer y Johnston (1972), pág. 499.
34. "Rueda de reacción/momento". NASA . Consultado el 15 de junio de 2018 .
35. Gurrisi, Charles; Seidel, Raymond; Dickerson, Scott; Didziulis, Stephen; Frantz, Peter; Ferguson, Kevin (12 de mayo de 2010). "Lecciones aprendidas con el giroscopio de momento de control de la estación espacial" (PDF) . Actas del 40.º Simposio sobre mecanismos aeroespaciales .

Referencias

• Anderson, John D. (2004), Introducción al vuelo (5.ª ed.), McGraw-Hill, ISBN 0-07-282569-3
• Bate, Roger B.; Mueller, Donald D.; White, Jerry E. (1971), Fundamentos de la astrodinámica , Dover
• Beer, Ferdinand P.; Johnston, Russell Jr. (1972), Mecánica vectorial para ingenieros: estática y dinámica , McGraw-Hill
• Drake, Bret G.; Baker, John D.; Hoffman, Stephan J.; Landau, Damon; Voels, Stephen A. (2017). "Opciones de trayectoria para explorar Marte y las lunas de Marte". Equipo de arquitectura de vuelos espaciales tripulados de la NASA (presentación) .
• Fellenz, DW (1967). "Atmospheric Entry". En Theodore Baumeister (ed.). Marks' Standard Handbook for Mechanical Engineers (Séptima edición). Nueva York: McGraw Hill. págs. 11:155–58. ISBN 0-07-142867-4.
• Glasstone, Samuel (1965). Libro de consulta sobre las ciencias espaciales. D. Van Nostrand Company, Inc.
• Hintz, Gerald R. (2015). Mecánica orbital y astrodinámica: técnicas y herramientas para misiones espaciales . Cham. ISBN 978-3-319-09444-1.OCLC 900730410  .{{cite book}}: CS1 maint: location missing publisher (link)
• Kromis, AJ (1967). "Análisis de trayectorias de vuelo con motor". En Theodore Baumeister (ed.). Marks' Standard Handbook for Mechanical Engineers (séptima edición). Nueva York: McGraw Hill. págs. 11:154–55. ISBN 0-07-142867-4.
• Mattfeld, Bryan; Stromgren, Chel; Shyface, Hilary; Komar, David R.; Cirillo, William; Goodliff, Kandyce (2015). Intercambios entre trayectorias de clases de oposición y conjunción para las primeras misiones humanas a Marte (PDF) (Informe) . Consultado el 10 de julio de 2018 .
• Perry, WR (1967). "Mecánica orbital". En Theodore Baumeister (ed.). Marks' Standard Handbook for Mechanical Engineers (séptima edición). Nueva York: McGraw Hill. págs. 11:151–52. ISBN 0-07-142867-4.
• Russell, JW (1967). "Mecánica de vuelo lunar e interplanetario". En Theodore Baumeister (ed.). Marks' Standard Handbook for Mechanical Engineers (séptima edición). Nueva York: McGraw-Hill. págs. 11:152–54. ISBN 0-07-142867-4.
• Sidi, MJ "Dinámica y control de naves espaciales". Cambridge, 1997.
• Thomson, WT "Introducción a la dinámica espacial". Dover, 1961.
• Wertz, JR "Determinación y control de la actitud de las naves espaciales". Kluwer, 1978.
• Wiesel, WE "Dinámica de los vuelos espaciales". McGraw-Hill, 1997.