El experimento de Fizeau [1] [2] [3] fue llevado a cabo por Hippolyte Fizeau en 1851 para medir las velocidades relativas de la luz en agua en movimiento. Fizeau utilizó un dispositivo especial de interferómetro para medir el efecto del movimiento de un medio sobre la velocidad de la luz.
Según las teorías que prevalecían en la época, la luz que viaja a través de un medio en movimiento sería arrastrada por el medio, de modo que la velocidad medida de la luz sería una simple suma de su velocidad a través del medio más la velocidad del medio. Fizeau detectó efectivamente un efecto de arrastre, pero la magnitud del efecto que observó fue mucho menor de lo esperado. Cuando repitió el experimento con aire en lugar de agua, no observó ningún efecto. Sus resultados aparentemente respaldaron la hipótesis de arrastre parcial del éter de Fresnel , una situación que desconcertó a la mayoría de los físicos. Pasó más de medio siglo antes de que se desarrollara una explicación satisfactoria de la inesperada medición de Fizeau con el advenimiento de la teoría de la relatividad especial de Albert Einstein . Einstein señaló más tarde la importancia del experimento para la relatividad especial, en la que corresponde a la fórmula relativista de adición de velocidades cuando se restringe a velocidades pequeñas.
Aunque se le conoce como el experimento de Fizeau, Fizeau fue un experimentador activo que llevó a cabo una amplia variedad de experimentos diferentes que implicaban medir la velocidad de la luz en diversas situaciones.


En la figura 2 se presenta una representación muy simplificada del experimento de Fizeau de 1851. La luz entrante se divide en dos haces mediante un divisor de haz (BS) y pasa a través de dos columnas de agua que fluyen en direcciones opuestas. Luego, los dos haces se recombinan para formar un patrón de interferencia que puede ser interpretado por un observador.
La disposición simplificada ilustrada en la figura 2 habría requerido el uso de luz monocromática, lo que habría permitido obtener sólo franjas tenues. Debido a la corta longitud de coherencia de la luz blanca , el uso de luz blanca habría requerido adaptar las trayectorias ópticas a un grado de precisión poco práctico, y el aparato habría sido extremadamente sensible a las vibraciones, los cambios de movimiento y los efectos de la temperatura.
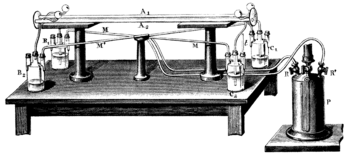
Por otra parte, el aparato de Fizeau, ilustrado en las figuras 3 y 4, estaba diseñado como un interferómetro de trayectoria común . Esto garantizaba que los rayos opuestos pasarían por trayectorias equivalentes, de modo que las franjas se formaban fácilmente incluso cuando se utilizaba el sol como fuente de luz.
El doble tránsito de la luz tenía por objeto aumentar la distancia recorrida en el medio en movimiento y, además, compensar por completo cualquier diferencia accidental de temperatura o presión entre los dos tubos, de la que pudiera resultar un desplazamiento de las franjas, que se mezclaría con el desplazamiento que el movimiento solo habría producido; y por lo tanto habría hecho incierta su observación. [P 1]
— Fizeau

Un rayo de luz que emana de la fuente S′ se refleja en un divisor de haz G y se colima en un haz paralelo mediante la lente L . Después de pasar por las rendijas O 1 y O 2 , dos rayos de luz viajan a través de los tubos A 1 y A 2 , a través de los cuales fluye agua de ida y vuelta como lo muestran las flechas. Los rayos se reflejan en un espejo m en el foco de la lente L′ , de modo que un rayo siempre se propaga en la misma dirección que la corriente de agua, y el otro rayo en dirección opuesta a la corriente de agua. Después de pasar de ida y vuelta a través de los tubos, ambos rayos se unen en S , donde producen franjas de interferencia que se pueden visualizar a través del ocular ilustrado. El patrón de interferencia se puede analizar para determinar la velocidad de la luz que viaja a lo largo de cada pata del tubo. [P 1] [P 2] [S 1]
Supongamos que el agua fluye por las tuberías con una velocidad v . Según la teoría no relativista del éter luminífero , la velocidad de la luz debería aumentar o disminuir cuando es "arrastrada" por el agua a través del marco del éter, dependiendo de la dirección. Según la hipótesis de arrastre completo del éter de Stokes , la velocidad total de un haz de luz debería ser una simple suma aditiva de su velocidad a través del agua más la velocidad del agua.
Es decir, si n es el índice de refracción del agua, de modo que c/n es la velocidad de la luz en el agua estacionaria, entonces la velocidad prevista de la luz w en un brazo sería
y la velocidad prevista en el otro brazo sería
Por lo tanto, la luz que viaja contra la corriente del agua debería ser más lenta que la luz que viaja a favor de la corriente del agua.
El patrón de interferencia entre los dos rayos cuando la luz se recombina en el observador depende de los tiempos de tránsito sobre los dos caminos y se puede utilizar para calcular la velocidad de la luz en función de la velocidad del agua. [S 2]
Fizeau descubrió que
En otras palabras, la luz parecía ser arrastrada por el agua, pero la magnitud del arrastre fue mucho menor de lo esperado.
El experimento de Fizeau obligó a los físicos a aceptar la validez empírica de una teoría más antigua de Augustin-Jean Fresnel (1818) que había sido invocada para explicar un experimento de Arago de 1810 , a saber, que un medio que se mueve a través del éter estacionario arrastra la luz que se propaga a través de él con solo una fracción de la velocidad del medio, con un coeficiente de arrastre f dado por
En 1895, Hendrik Lorentz predijo la existencia de un término extra debido a la dispersión : [S 3] : 15–20
Como el medio fluye hacia el observador o se aleja de él, la luz que viaja a través del medio sufre un desplazamiento Doppler, y el índice de refracción utilizado en la fórmula tiene que ser el apropiado para la longitud de onda desplazada por el efecto Doppler. [P 3] Zeeman verificó la existencia del término de dispersión de Lorentz en 1915. [P 4]
Más tarde resultó que el coeficiente de arrastre de Fresnel efectivamente concuerda con la fórmula de adición de velocidad relativista, véase la sección Derivación en relatividad especial.

Albert A. Michelson y Edward W. Morley (1886) [P 5] repitieron el experimento de Fizeau con una precisión mejorada, abordando varias preocupaciones con el experimento original de Fizeau: (1) La deformación de los componentes ópticos en el aparato de Fizeau podría causar desplazamiento de franjas por artefactos; (2) las observaciones se apresuraron, ya que el flujo de agua presurizado duró solo un corto tiempo; (3) el perfil de flujo laminar del agua que fluía a través de los tubos de diámetro pequeño de Fizeau significaba que solo estaban disponibles sus porciones centrales, lo que resultaba en franjas tenues; (4) había incertidumbres en la determinación de Fizeau de la velocidad de flujo a través del diámetro de los tubos. Michelson rediseñó el aparato de Fizeau con tubos de mayor diámetro y un gran depósito que proporcionaba tres minutos de flujo de agua constante. Su diseño de interferómetro de trayectoria común proporcionó una compensación automática de la longitud de la trayectoria, de modo que las franjas de luz blanca eran visibles de inmediato tan pronto como se alineaban los elementos ópticos. Topológicamente, la trayectoria de la luz era la de un interferómetro de Sagnac con un número par de reflexiones en cada trayectoria de luz. [S 4] Esto ofrecía franjas extremadamente estables que eran, en primer orden, completamente insensibles a cualquier movimiento de sus componentes ópticos. La estabilidad era tal que le era posible insertar una placa de vidrio en h o incluso sostener una cerilla encendida en la trayectoria de la luz sin desplazar el centro del sistema de franjas. Utilizando este aparato, Michelson y Morley pudieron confirmar completamente los resultados de Fizeau no sólo en el agua, sino también en el aire. [P 5]
Pieter Zeeman realizó otros experimentos entre 1914 y 1915. Utilizando una versión ampliada del aparato de Michelson conectada directamente al conducto principal de agua de Ámsterdam , Zeeman pudo realizar mediciones ampliadas utilizando luz monocromática que abarcaba desde el violeta (4358 Å) hasta el rojo (6870 Å) para confirmar el coeficiente modificado de Lorentz. [P 6] [P 4] En 1910, Franz Harress utilizó un dispositivo giratorio y confirmó en general el coeficiente de arrastre de Fresnel. Sin embargo, también encontró un "sesgo sistemático" en los datos, que más tarde resultó ser el efecto Sagnac . [S 5]
Desde entonces, se han llevado a cabo muchos experimentos para medir dichos coeficientes de arrastre en una diversidad de materiales con diferentes índices de refracción, a menudo en combinación con el efecto Sagnac. [S 6] Por ejemplo, en experimentos que utilizan láseres de anillo junto con discos giratorios, [P 7] [P 8] [P 9] [P 10] o en experimentos de interferometría de neutrones . [P 11] [P 12] [P 13] También se observó un efecto de arrastre transversal, es decir, cuando el medio se mueve en ángulos rectos a la dirección de la luz incidente. [P 3] [P 14]
Martin Hoek (1868) proporcionó una confirmación indirecta del coeficiente de arrastre de Fresnel . [P 15] [S 7] Su aparato era similar al de Fizeau, aunque en su versión sólo un brazo contenía un área llena de agua en reposo, mientras que el otro brazo estaba en el aire. Como lo ve un observador que descansa en el éter, la Tierra y, por lo tanto, el agua están en movimiento. Por lo tanto, Hoek calculó los siguientes tiempos de viaje de dos rayos de luz que viajan en direcciones opuestas (sin tener en cuenta la dirección transversal, véase la imagen):
Los tiempos de viaje no son los mismos, lo que debería indicarse mediante un desplazamiento de interferencia. Sin embargo, si se aplica el coeficiente de arrastre de Fresnel al agua en el marco del éter, la diferencia de tiempo de viaje (de primer orden en v/c ) desaparece. Utilizando diferentes configuraciones, Hoek obtuvo un resultado nulo, lo que confirma el coeficiente de arrastre de Fresnel. (Para un experimento similar que refuta la posibilidad de proteger el viento del éter, consulte el experimento de Hammar ).
En la versión particular del experimento que se muestra aquí, Hoek utilizó un prisma P para dispersar la luz desde una rendija en un espectro que pasaba por un colimador C antes de entrar en el aparato. Con el aparato orientado en paralelo al viento de éter hipotético, Hoek esperaba que la luz en un circuito se retardara 7/600 mm con respecto al otro. Cuando este retardo representaba un número entero de longitudes de onda, esperaba ver interferencia constructiva; cuando este retardo representaba un número medio entero de longitudes de onda, esperaba ver interferencia destructiva. En ausencia de arrastre, su expectativa era que el espectro observado fuera continuo con el aparato orientado transversalmente al viento de éter, y que estuviera en bandas con el aparato orientado en paralelo al viento de éter. Sus resultados experimentales reales fueron completamente negativos. [P 15] [S 7]
Aunque la hipótesis de Fresnel fue empíricamente exitosa para explicar los resultados de Fizeau, muchos expertos en el campo, incluido el propio Fizeau (1851), Éleuthère Mascart (1872), Ketteler (1873), Veltmann (1873) y Lorentz (1886) encontraron el razonamiento mecánico de Fresnel para el arrastre parcial del éter desagradable por varias razones. Por ejemplo, Veltmann (1870) explica que la hipótesis de Fresnel se propuso como una "supuesta compensación" de la aberración que "cancelará exactamente" la desviación del experimento de Arago. Luego continúa demostrando un método para usar el éter completamente arrastrado de Stokes en lugar de la hipótesis de Fresnel que aún sería "necesaria al final del desarrollo". Al final vuelve al principio de Fresnel enfatizando que es una relación matemática que representa un "principio común" a una "clase de explicaciones" de la aberración de la luz de las estrellas aclarando:
La velocidad con la que el movimiento de la luz interviene en el movimiento del medio depende de la velocidad de propagación y, por tanto, debe ser diferente para cada color. (traducción de Google) Die Geschwindigkeit, mit welcher die Lichtbewegung an der Bewegung des Mediums theilnimmt, hängt von der Fortpflanzungsgeschwindigkeit ab und müsste deshalb für jede Farbe eine andere sein.
Esta línea se puede traducir más directamente como "la velocidad con la que el movimiento de la luz al movimiento del medio [material] depende [, también depende] de la velocidad de propagación [en el medio] y por lo tanto [hay] necesaria una diferente para cada color". Confirmando así el principio matemático de Fresnel (pero no su explicación) de que la velocidad a la que un medio afecta la velocidad de la luz depende del índice de refracción que ya se había establecido como una medida de alteraciones de la velocidad de la luz dependiente de la frecuencia.
Sin embargo, el historiador Stachel en 2005 nos da una interpretación diferente que supone que "uno para cada color" significa éter en lugar de diferentes "tasas" o "velocidades".
Veltmann (1870) demuestra experimentalmente que la fórmula de Fresnel debe aplicarse utilizando el índice de refracción apropiado (diferente) para cada color de luz. Esto significa que, independientemente de cómo se mueva el éter, debe moverse de manera diferente para cada frecuencia de luz. Pero ¿qué sucede cuando la luz blanca (o cualquier mezcla de frecuencias) pasa a través de un medio transparente? [S 8]
Mascart (1872) demostró que la luz polarizada que viaja a través de un medio birrefringente es insensible al movimiento de la Tierra. Después de establecer que la teoría de Fresnel representa un mecanismo compensatorio exacto que cancela los efectos de aberración, analiza otros mecanismos compensatorios exactos en sistemas de ondas mecánicas, incluida la insensibilidad al efecto Doppler de los experimentos de movimiento conjunto. Concluye que "la fórmula [de Fresnel] no es aplicable a medios birrefringentes". Finalizó este informe sobre sus experimentos en medios birrefringentes con su hallazgo de que el experimento en medios anisotrópicos produjo una cantidad resultante que era "cuatro veces menor que la que obtendríamos al aplicar a la propagación de ondas polarizadas circularmente la fórmula demostrada por Fresnel para el caso de cuerpos isotrópicos".
El propio Fizeau demuestra que era consciente de la viabilidad mecánica de la hipótesis de Fresnel anteriormente en su informe, pero la sorpresa de Fizeau y las expectativas desafiadas del arrastre total de Stokes se insinuaron en la conclusión del informe:
Por último, si sólo se lleva una parte del éter, la velocidad de la luz aumentará, pero sólo en una fracción de la velocidad del cuerpo y no, como en la primera hipótesis, en toda la velocidad. Esta consecuencia no es tan obvia como la anterior, pero Fresnel ha demostrado que puede apoyarse en argumentos mecánicos de gran probabilidad. [...] El éxito del experimento me parece que hace necesaria la adopción de la hipótesis de Fresnel, o al menos de la ley que él encontró para la expresión de la alteración de la velocidad de la luz por efecto del movimiento de un cuerpo; pues aunque el hecho de que esa ley sea verdadera puede ser una prueba muy sólida en favor de la hipótesis de la que es sólo una consecuencia, tal vez la concepción de Fresnel pueda parecer tan extraordinaria y, en algunos aspectos, tan difícil de admitir, que todavía serán necesarias otras pruebas y un examen profundo por parte de los geómetras antes de adoptarla como expresión de los hechos reales del caso. [P 1]
A pesar de la insatisfacción de la mayoría de los físicos [ cita requerida ] con la hipótesis de Fresnel sobre el arrastre parcial del éter, las repeticiones y mejoras del experimento de Fizeau (ver secciones anteriores) realizadas por otros confirmaron sus resultados con gran precisión.
Además de los experimentos de Mascart que demostraron una insensibilidad al movimiento de la Tierra y las quejas sobre la hipótesis del arrastre parcial del éter, surgió otro problema importante con el experimento de Michelson-Morley (1887). Las afirmaciones de Mascart de que los experimentos ópticos de refracción y reflexión serían insensibles al movimiento de la Tierra fueron probadas por este experimento posterior. En la teoría de Fresnel, el éter es casi estacionario y la Tierra se mueve a través de él, por lo que el experimento debería haber dado un resultado parcialmente reducido, pero neto positivo. Solo un arrastre completo del éter por el medio del aire daría como resultado un valor nulo. Sin embargo, el resultado de este experimento se informó como nulo. Por lo tanto, desde el punto de vista de los modelos de éter en ese momento, la situación experimental era contradictoria: por un lado, la aberración de la luz , el experimento de Fizeau y su repetición por Michelson y Morley en 1886 parecían apoyar solo un pequeño grado de arrastre del éter. Por otra parte, el experimento de Michelson-Morley de 1887 pareció demostrar que el éter está en reposo con respecto a la Tierra, aparentemente apoyando la idea del arrastre completo del éter (ver hipótesis del arrastre del éter ). [S 9] De modo que el éxito de la hipótesis de Fresnel para explicar los resultados de Fizeau ayudó a conducir a una crisis teórica, que sólo se resolvió con la introducción de la teoría relativista.
¿Es fantástico imaginar que alguien pudiera haber sido llevado a desarrollar algunas o todas estas respuestas cinemáticas al desafío que presentaba la situación en la óptica de los cuerpos en movimiento alrededor de 1880, dado que Mascart ya había formulado un principio óptico del movimiento relativo? Tal vez no sea más fantástico que lo que realmente sucedió: el desarrollo por parte de Einstein alrededor de 1905 de una respuesta cinemática al desafío que presentaba la situación en la electrodinámica de los cuerpos en movimiento, dado que Poincaré ya había formulado un principio electrodinámico del movimiento relativo. [S 8]
En 1892, Hendrik Lorentz propuso una modificación del modelo de Fresnel, en el que el éter es completamente estacionario. Logró derivar el coeficiente de arrastre de Fresnel como resultado de una interacción entre el agua en movimiento y un éter no arrastrado. [S 9] [S 10] : 25–30 También descubrió que la transición de un sistema de referencia a otro podía simplificarse utilizando una variable de tiempo auxiliar que llamó tiempo local :
En 1895, Lorentz explicó de forma más general el coeficiente de Fresnel basándose en el concepto de tiempo local. Sin embargo, la teoría de Lorentz tenía el mismo problema fundamental que la de Fresnel: un éter estacionario contradecía el experimento de Michelson-Morley . Así, en 1892, Lorentz propuso que los cuerpos en movimiento se contraen en la dirección del movimiento ( hipótesis de contracción de FitzGerald-Lorentz , ya que George FitzGerald había llegado a esta conclusión en 1889). Las ecuaciones que utilizó para describir estos efectos fueron desarrolladas por él hasta 1904. Estas ahora se denominan transformaciones de Lorentz en su honor, y son idénticas en forma a las ecuaciones que Einstein derivaría más tarde a partir de los primeros principios. Sin embargo, a diferencia de las ecuaciones de Einstein, las transformaciones de Lorentz eran estrictamente ad hoc , y su única justificación era que parecían funcionar. [S 9] [S 10] : 27–30
Einstein demostró cómo las ecuaciones de Lorentz podían derivarse como el resultado lógico de un conjunto de dos postulados iniciales simples. Además, Einstein reconoció que el concepto de éter estacionario no tiene lugar en la relatividad especial, y que la transformación de Lorentz concierne a la naturaleza del espacio y el tiempo. Junto con el problema del imán y el conductor en movimiento , los experimentos de deriva negativa del éter y la aberración de la luz , el experimento de Fizeau fue uno de los resultados experimentales clave que moldearon el pensamiento de Einstein sobre la relatividad. [S 11] [S 12] Robert S. Shankland informó sobre algunas conversaciones con Einstein, en las que Einstein enfatizó la importancia del experimento de Fizeau: [S 13]
Agregó que los resultados experimentales que más lo habían influenciado fueron las observaciones de la aberración estelar y las mediciones de Fizeau sobre la velocidad de la luz en el agua en movimiento. "Fueron suficientes", dijo.
Max von Laue (1907) demostró que el coeficiente de arrastre de Fresnel puede explicarse fácilmente como una consecuencia natural de la fórmula relativista para la suma de velocidades , [S 14] a saber:
El experimento de Fizeau es, por tanto, una prueba que apoya el caso colineal de la fórmula de adición de velocidades de Einstein. [P 16]
Fuentes secundarias