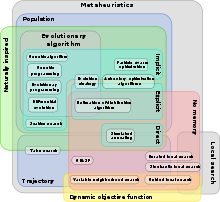
Esta es una lista ordenada cronológicamente de metaheurísticas basadas en metáforas y algoritmos de inteligencia de enjambre , ordenados por década de propuesta.

El recocido simulado es un algoritmo probabilístico inspirado en el recocido , un método de tratamiento térmico en metalurgia . Se utiliza a menudo cuando el espacio de búsqueda es discreto (por ejemplo, todos los recorridos que visitan un conjunto determinado de ciudades). Para los problemas en los que encontrar el óptimo global preciso es menos importante que encontrar un óptimo local aceptable en una cantidad fija de tiempo, el recocido simulado puede ser preferible a alternativas como el descenso de gradiente .
El análogo del enfriamiento lento del recocido es una disminución lenta de la probabilidad de que el recocido simulado acepte soluciones peores a medida que explora el espacio de soluciones. Aceptar soluciones peores es una propiedad fundamental de las metaheurísticas porque permite una búsqueda más extensa de la solución óptima.
El algoritmo de optimización de colonias de hormigas es una técnica probabilística para resolver problemas computacionales que se pueden reducir a encontrar buenos caminos a través de grafos . Inicialmente propuesto por Marco Dorigo en 1992 en su tesis doctoral, [1] [2] el primer algoritmo tenía como objetivo buscar un camino óptimo en un grafo basado en el comportamiento de las hormigas que buscan un camino entre su colonia y una fuente de alimento. La idea original se ha diversificado desde entonces para resolver una clase más amplia de problemas numéricos y, como resultado, han surgido varios problemas [ ejemplo necesario ] , que se basan en varios aspectos del comportamiento de las hormigas. Desde una perspectiva más amplia, ACO realiza una búsqueda basada en modelos [3] y comparte algunas similitudes con los algoritmos de estimación de distribución .
La optimización por enjambre de partículas es un método computacional que optimiza un problema al intentar iterativamente mejorar una solución candidata con respecto a una medida dada de calidad. Resuelve un problema al tener una población de soluciones candidatas, denominadas partículas , y al mover estas partículas en el espacio de búsqueda de acuerdo con fórmulas matemáticas simples [ ¿cuál? ] sobre la posición y velocidad de la partícula . El movimiento de cada partícula está influenciado por su mejor posición local conocida, pero también se guía hacia las posiciones más conocidas en el espacio de búsqueda, que se actualizan a medida que otras partículas encuentran mejores posiciones. Se espera que esto mueva el enjambre hacia las mejores soluciones.
El algoritmo PSO se atribuye originalmente a Kennedy , Eberhart y Shi [4] [5] y fue pensado inicialmente para simular el comportamiento social [6] como una representación estilizada del movimiento de organismos en una bandada de pájaros o un banco de peces . El algoritmo se simplificó y se observó que realizaba una optimización. El libro de Kennedy y Eberhart [7] describe muchos aspectos filosóficos del algoritmo PSO y la inteligencia de enjambre . Poli realizó un estudio extenso de las aplicaciones del algoritmo PSO . [8] [9] Bonyadi y Michalewicz publicaron una revisión exhaustiva de trabajos teóricos y experimentales sobre el algoritmo PSO. [10]
La búsqueda de armonía es una metaheurística que imita fenómenos introducida en 2001 por Zong Woo Geem, Joong Hoon Kim y GV Loganathan [11] y está inspirada en el proceso de improvisación de los músicos de jazz. En el algoritmo HS, se genera aleatoriamente un conjunto de posibles soluciones (llamado memoria de armonía). Se genera una nueva solución utilizando todas las soluciones en la memoria de armonía (en lugar de solo dos como se usa en GA) y si esta nueva solución es mejor que la peor solución en la memoria de armonía, la peor solución se reemplaza por esta nueva solución. La efectividad y las ventajas de HS se han demostrado en varias aplicaciones como el diseño de redes de distribución de agua municipales, [12] diseño estructural, [13] problema de despacho de carga en ingeniería eléctrica, [14] optimización multiobjetivo, [15] problemas de programación, [16] agrupamiento, [17] y clasificación y selección de características. [18] [19] Se puede encontrar un estudio detallado sobre las aplicaciones de HS. [20] [21] y las aplicaciones de HS en minería de datos se pueden encontrar en. [22]
Dennis (2015) afirmó que la búsqueda de armonía es un caso especial del algoritmo de estrategias de evolución . [23] Sin embargo, Saka et al. (2016) sostiene que la estructura de las estrategias de evolución es diferente de la de la búsqueda de armonía. [24]
El algoritmo de colonia de abejas artificiales es una metaheurística introducida por Karaboga en 2005 [25] que simula el comportamiento de búsqueda de alimento de las abejas melíferas . El algoritmo ABC tiene tres fases: abeja empleada, abeja observadora y abeja exploradora. En las fases de abeja empleada y abeja observadora, las abejas explotan las fuentes mediante búsquedas locales en las proximidades de las soluciones seleccionadas en función de la selección determinista en la fase de abeja empleada y la selección probabilística en la fase de abeja observadora. En la fase de abeja exploradora, que es análoga a las abejas que abandonan las fuentes de alimento agotadas en el proceso de búsqueda de alimento, se abandonan las soluciones que ya no son beneficiosas para el progreso de la búsqueda y se insertan nuevas soluciones en su lugar para explorar nuevas regiones en el espacio de búsqueda. El algoritmo tiene una capacidad de exploración y explotación bien equilibrada [ palabras confusas ] . [ aclaración necesaria ]
El algoritmo de las abejas fue formulado por Pham y sus colaboradores en 2005 [26] y refinado en 2009. [27] Modelado sobre el comportamiento de búsqueda de alimento de las abejas melíferas , el algoritmo combina la búsqueda exploratoria global con la búsqueda explotadora local. Un pequeño número de abejas artificiales (exploradoras) explora aleatoriamente el espacio de soluciones (entorno) para soluciones de alta aptitud (fuentes de alimento altamente rentables), mientras que la mayor parte de la población busca (cosecha) el vecindario de las soluciones más aptas buscando el óptimo de aptitud. Se utiliza un procedimiento de reclutamiento determinista que simula la danza de meneo de las abejas biológicas para comunicar los hallazgos de las exploradoras a las recolectoras y distribuirlas dependiendo de la aptitud de los vecindarios seleccionados para la búsqueda local. Una vez que la búsqueda en el vecindario de una solución se estanca, se considera que se encontró el óptimo de aptitud local y se abandona el sitio.
El algoritmo competitivo imperialista (ICA), como la mayoría de los métodos en el área de computación evolutiva , no necesita el gradiente de la función en su proceso de optimización. Desde un punto de vista específico, el ICA puede considerarse como la contraparte social de los algoritmos genéticos (AG). El ICA es el modelo matemático y la simulación por computadora de la evolución social humana , mientras que los AG se basan en la evolución biológica de las especies.
Este algoritmo comienza generando un conjunto de soluciones candidatas aleatorias en el espacio de búsqueda del problema de optimización. Los puntos aleatorios generados se denominan Países iniciales . Los países en este algoritmo son la contraparte de los Cromosomas en AGs y Partículas en Optimización por Enjambre de Partículas y es una matriz de valores de una solución candidata del problema de optimización. La función de costo del problema de optimización determina el poder de cada país. Con base en su poder, algunos de los mejores países iniciales (los países con el menor valor de función de costo), se convierten en Imperialistas y comienzan a tomar el control de otros países (llamados colonias ) y forman los Imperios iniciales . [28]
Los dos operadores principales de este algoritmo son la asimilación y la revolución . La asimilación hace que las colonias de cada imperio se acerquen al estado imperialista en el espacio de características sociopolíticas (espacio de búsqueda de optimización). La revolución provoca cambios aleatorios repentinos en la posición de algunos de los países en el espacio de búsqueda. Durante la asimilación y la revolución, una colonia podría alcanzar una mejor posición y luego tener la oportunidad de tomar el control de todo el imperio y reemplazar al estado imperialista actual del imperio. [29]
La competencia imperialista es otra parte de este algoritmo. Todos los imperios intentan ganar este juego y tomar posesión de las colonias de otros imperios. En cada paso del algoritmo, en función de su poder, todos los imperios tienen la posibilidad de tomar el control de una o más de las colonias del imperio más débil. [28]
El algoritmo continúa con los pasos mencionados (Asimilación, Revolución, Competencia) hasta que se satisface una condición de parada.
Los pasos anteriores se pueden resumir en el siguiente pseudocódigo : [30] [29]
0) Defina la función objetivo:1) Inicialización del algoritmo. Generar una solución aleatoria en el espacio de búsqueda y crear imperios iniciales. 2) Asimilación: Las colonias se mueven hacia los estados imperialistas en diferentes direcciones. 3) Revolución: Se producen cambios aleatorios en las características de algunos países. 4) Intercambio de posiciones entre una colonia y un imperialista. Una colonia con una posición mejor que la del imperialista, tiene la oportunidad de tomar el control del imperio reemplazando al imperialismo existente. 5) Competencia imperialista: Todos los imperialistas compiten para tomar posesión de las colonias de los demás. 6) Eliminar los imperios débiles. Los imperios débiles pierden su poder gradualmente y finalmente serán eliminados. 7) Si se cumple la condición de parada, deténgase, si no, pase al paso 2.8) FinLa dinámica de formación de ríos se basa en imitar cómo el agua forma ríos erosionando el suelo y depositando sedimentos (las gotas actúan como enjambre). Después de que las gotas transforman el paisaje aumentando/disminuyendo la altitud de los lugares, se dan soluciones en forma de caminos de altitudes decrecientes. Se construyen gradientes decrecientes, y estos gradientes son seguidos por gotas posteriores para componer nuevos gradientes y reforzar los mejores. Este método de optimización heurística fue propuesto en 2007 por Rabanal et al. [31] Se ha estudiado la aplicabilidad de RFD a otros problemas NP-completos [32] y el algoritmo se ha aplicado a campos como el enrutamiento [33] y la navegación de robots [34] . Las principales aplicaciones de RFD se pueden encontrar en la encuesta Rabanal et al. (2017). [35]
El algoritmo de búsqueda gravitacional se basa en la ley de la gravedad y la noción de interacciones de masas. El algoritmo GSA utiliza la teoría de la física newtoniana y sus agentes buscadores son la colección de masas. En GSA, hay un sistema aislado de masas. Usando la fuerza gravitacional, cada masa en el sistema puede ver la situación de otras masas. La fuerza gravitacional es por lo tanto una forma de transferir información entre diferentes masas. [36] En GSA, los agentes son considerados como objetos y su desempeño se mide por sus masas. Todos estos objetos se atraen entre sí por una fuerza de gravedad , y esta fuerza causa el movimiento de todos los objetos hacia los objetos con masas más pesadas. Las masas más pesadas corresponden a mejores soluciones del problema. La posición del agente corresponde a una solución del problema, y su masa se determina usando una función de aptitud. Con el paso del tiempo, las masas son atraídas por la masa más pesada, que idealmente presentaría una solución óptima en el espacio de búsqueda. El GSA podría considerarse como un pequeño mundo artificial de masas que obedecen las leyes newtonianas de gravitación y movimiento. [37] Hassanzadeh et al. propusieron en 2010 una variante multiobjetivo de GSA, denominada MOGSA. [38]
El algoritmo de murciélagos es un algoritmo basado en inteligencia de enjambre, inspirado en el comportamiento de ecolocalización de los micro murciélagos . BA equilibra automáticamente la exploración (saltos de largo alcance alrededor del espacio de búsqueda global para evitar quedarse atascado alrededor de un máximo local) con la explotación (búsqueda con más detalle alrededor de soluciones buenas conocidas para encontrar máximos locales) al controlar la sonoridad y las tasas de emisión de pulsos de murciélagos simulados en el espacio de búsqueda multidimensional. [39]
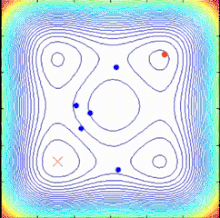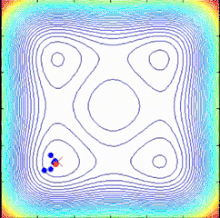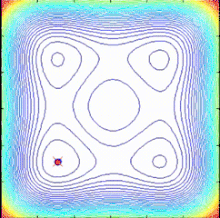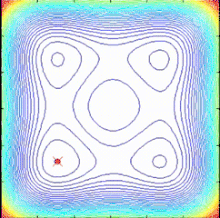
El algoritmo de optimización en espiral, inspirado en los fenómenos espirales de la naturaleza, es un algoritmo de búsqueda multipunto que no tiene gradiente de función objetivo. Utiliza múltiples modelos espirales que pueden describirse como sistemas dinámicos deterministas. A medida que los puntos de búsqueda siguen trayectorias espirales logarítmicas hacia el centro común, definido como el mejor punto actual, se pueden encontrar mejores soluciones y se puede actualizar el centro común. [40]
La inteligencia artificial en enjambre es un sistema de circuito cerrado en tiempo real de usuarios humanos conectados a través de Internet y estructurado en un marco modelado a partir de enjambres naturales, de modo que evoca la sabiduría colectiva del grupo como una inteligencia emergente unificada. [41] [42] De esta manera, los enjambres humanos pueden responder preguntas, hacer predicciones, tomar decisiones y resolver problemas explorando colectivamente un conjunto diverso de opciones y convergiendo en soluciones preferidas en sincronía. Inventada por el Dr. Louis Rosenberg en 2014, la metodología ASI se ha destacado por su capacidad para hacer predicciones colectivas precisas que superan a los miembros individuales del enjambre. [43] En 2016, un grupo de Inteligencia Artificial en Enjambre de Unanimous AI fue desafiado por un reportero a predecir los ganadores del Derby de Kentucky ; eligió con éxito los primeros cuatro caballos, en orden, superando las probabilidades de 540 a 1. [44] [45]
Las metaheurísticas de autoajuste han surgido como un avance significativo en el campo de los algoritmos de optimización en los últimos años, ya que el ajuste fino puede ser un proceso muy largo y difícil. [46] Estos algoritmos se diferencian por su capacidad de ajustar de forma autónoma sus parámetros en respuesta al problema en cuestión, mejorando la eficiencia y la calidad de la solución. Esta capacidad de autoajuste es particularmente importante en escenarios de optimización complejos donde los métodos tradicionales pueden tener dificultades debido a la configuración rígida de los parámetros. En este intento, ya se ha introducido una variante de PSO que adopta la lógica difusa para calcular automáticamente los parámetros de cada partícula [47], así como la optimización Flying Fox, que es un optimizador de autoajuste difuso. [48]
La aparición de variantes de autoajuste en las metaheurísticas marca un cambio fundamental hacia herramientas de optimización más autónomas. Estos algoritmos de autoajuste reducen significativamente la necesidad de intervención experta en el ajuste de parámetros, un proceso que requiere un amplio conocimiento del dominio. Al aprovechar la lógica difusa y otros mecanismos adaptativos, estos algoritmos pueden ajustar de forma inteligente sus parámetros en respuesta a las características del problema y la dinámica del espacio de búsqueda. Esta autonomía no solo simplifica el proceso de optimización, sino que también amplía la aplicabilidad de estos algoritmos, haciéndolos más accesibles y efectivos para una gama más amplia de usuarios y problemas complejos. La capacidad de estas metaheurísticas de autoajuste para funcionar de manera efectiva sin un ajuste perfecto por parte del usuario representa un avance considerable para hacer que la optimización sea más fácil de usar y eficiente.
Si bien las metaheurísticas inspiradas en metáforas individuales han producido soluciones notablemente efectivas para problemas específicos, [49] las metaheurísticas inspiradas en metáforas en general han atraído críticas entre los investigadores por ocultar su falta de efectividad o novedad detrás de metáforas elaboradas. [49] [50] Kenneth Sörensen señaló: [51]
En los últimos años, el campo de la optimización combinatoria ha sido testigo de un verdadero tsunami de métodos metaheurísticos "novedosos", la mayoría de ellos basados en una metáfora de algún proceso natural o creado por el hombre. El comportamiento de prácticamente cualquier especie de insectos, el flujo del agua, unos músicos tocando juntos... parece que ninguna idea es demasiado descabellada para servir de inspiración para lanzar otra metaheurística. [Yo] argumentaré que esta línea de investigación amenaza con alejar el área de las metaheurísticas del rigor científico.
Sörensen y Glover declararon: [52]
Un gran (y creciente) número de publicaciones se centra en el desarrollo de (supuestamente) nuevos marcos metaheurísticos basados en metáforas. La lista de procesos naturales o creados por el hombre que se ha utilizado como base para un marco metaheurístico ahora incluye procesos tan diversos como la búsqueda de alimento por parte de bacterias, la formación de ríos, la biogeografía, los músicos tocando juntos, el electromagnetismo, la gravedad, la colonización por un imperio , las explosiones de minas, los campeonatos de liga, las nubes, etc. Una subcategoría importante se encuentra en las metaheurísticas basadas en el comportamiento animal. Las hormigas , las abejas , los murciélagos , los lobos, los gatos, las luciérnagas, las águilas, los delfines, las ranas , el salmón, los buitres, las termitas, las moscas y muchos otros, se han utilizado para inspirar una metaheurística "novedosa". [...] Como regla general, la publicación de artículos sobre metaheurísticas basadas en metáforas se ha limitado a revistas y conferencias de segundo nivel, pero se pueden encontrar algunas excepciones recientes a esta regla. Sörensen (2013) afirma que la investigación en esta dirección tiene fallas fundamentales. Lo más importante es que el autor sostiene que la novedad de la metáfora subyacente no hace automáticamente que el marco resultante sea "novedoso". Por el contrario, hay cada vez más evidencia de que muy pocos de los métodos basados en metáforas son nuevos en algún sentido interesante.
En respuesta, el Journal of Heuristics de Springer ha actualizado su política editorial para indicar: [53]
Proponer nuevos paradigmas sólo es aceptable si contienen ideas básicas innovadoras, como las que están incorporadas en marcos clásicos como los algoritmos genéticos , la búsqueda tabú y el recocido simulado . El Journal of Heuristics evita la publicación de artículos que reempaquetan e incorporan viejas ideas en métodos que se afirma que están basados en metáforas de sistemas y procesos naturales o artificiales. Estos métodos denominados "novedosos" emplean analogías que van desde gotas de agua inteligentes , músicos tocando jazz, sociedades imperialistas , ranas saltadoras , canguros, todo tipo de enjambres e insectos e incluso procesos de explosión de minas (Sörensen, 2013). Si un investigador utiliza una metáfora para estimular sus propias ideas sobre un nuevo método, el método debe, no obstante, traducirse a un lenguaje libre de metáforas, de modo que las estrategias empleadas puedan entenderse claramente y su novedad se haga claramente visible. (Véanse los puntos 2 y 3 a continuación). Las metáforas son baratas y fáciles de conseguir. Su uso para "maquillar" un método no es aceptable.
[...] Las implementaciones deben explicarse empleando la terminología de optimización estándar, donde una solución se denomina "solución" y no algo más relacionado con alguna metáfora oscura (por ejemplo, armonía, moscas , murciélagos , países , etc.).
[...] El Journal of Heuristics respalda plenamente la opinión de Sörensen de que los métodos “novedosos” basados en metáforas no deberían publicarse si no pueden demostrar una contribución a su campo. Cambiar el nombre de los conceptos existentes no cuenta como una contribución. Aunque estos métodos a menudo se denominan “novedosos”, muchos no presentan ideas nuevas, excepto por la variante marginal ocasional de una metodología ya existente. Estos métodos no deberían ocupar el espacio de la revista de ideas e investigaciones verdaderamente innovadoras. Dado que no utilizan el vocabulario estándar de optimización, son innecesariamente difíciles de entender.
La política de la revista 4OR - A Quarterly Journal of Operations Research de Springer establece: [54]
El énfasis en el rigor científico y en la innovación implica, en particular, que la revista no publique artículos que simplemente propongan variantes disfrazadas de métodos conocidos sin una validación adecuada (por ejemplo, metaheurísticas que se afirma que son "eficaces" sobre la base de comparaciones metafóricas con sistemas y procesos naturales o artificiales). Los nuevos métodos deben presentarse en un lenguaje libre de metáforas, estableciendo su relación con los paradigmas clásicos. Sus propiedades deben establecerse sobre la base de argumentos científicamente convincentes: pruebas matemáticas, experimentos controlados, comparaciones objetivas, etc.
Las Transacciones ACM sobre Optimización del Aprendizaje Evolutivo y la revista Evolutionary Computation también incluyen declaraciones similares. [55] [56]