El modelado de superficies de forma libre es una técnica para diseñar superficies de forma libre con un sistema CAD o CAID .
La tecnología ha abarcado dos campos principales: la creación de superficies estéticas ( superficies de clase A ) que también cumplen una función; por ejemplo, carrocerías de automóviles y formas exteriores de productos de consumo, o superficies técnicas para componentes como álabes de turbinas de gas y otros componentes de ingeniería de dinámica de fluidos.
Los paquetes de software CAD utilizan dos métodos básicos para la creación de superficies. El primero comienza con curvas de construcción ( splines ) a partir de las cuales se barre (secciona a lo largo del riel guía) o se enmalla (loftea) la superficie 3D.

El segundo método es la creación directa de la superficie con manipulación de los polos de la superficie/puntos de control.

A partir de estas superficies creadas inicialmente, se construyen otras superficies utilizando métodos derivados, como extensiones desplazadas o en ángulo de las superficies, o mediante puentes y combinaciones entre grupos de superficies.

Las superficies de forma libre , o superficies de forma libre , se utilizan en CAD y otros programas de gráficos por ordenador para describir la piel de un elemento geométrico 3D. Las superficies de forma libre no tienen dimensiones radiales rígidas, a diferencia de las superficies regulares como planos , cilindros y superficies cónicas . Se utilizan para describir formas como álabes de turbinas , carrocerías de automóviles y cascos de barcos . Inicialmente desarrolladas para las industrias automotriz y aeroespacial , las superficies de forma libre se utilizan ahora ampliamente en todas las disciplinas de diseño de ingeniería, desde productos de consumo hasta barcos. La mayoría de los sistemas actuales utilizan matemáticas B-spline racionales no uniformes (NURBS) [1] para describir las formas de la superficie; sin embargo, existen otros métodos como las superficies de Gordon o las superficies de Coons .
Las formas de las superficies (y curvas) de forma libre no se almacenan ni se definen en el software CAD en términos de ecuaciones polinómicas , sino por sus polos, grado y número de parches (segmentos con curvas spline). El grado de una superficie determina sus propiedades matemáticas y puede verse como la representación de la forma mediante un polinomio con variables a la potencia del valor del grado. Por ejemplo, una superficie con un grado de 1 sería una superficie de sección transversal plana . Una superficie con un grado de 2 estaría curvada en una dirección, mientras que una superficie de grado 3 podría (pero no necesariamente) cambiar una vez de curvatura cóncava a convexa. Algunos sistemas CAD utilizan el término orden en lugar de grado . El orden de un polinomio es uno mayor que el grado y da el número de coeficientes en lugar del mayor exponente .

Los polos (a veces conocidos como puntos de control ) de una superficie definen su forma. Los bordes naturales de la superficie están definidos por las posiciones del primer y último polo. (Tenga en cuenta que una superficie puede tener límites recortados). Los polos intermedios actúan como imanes que atraen la superficie en su dirección. Sin embargo, la superficie no pasa por estos puntos. El segundo y tercer polo, además de definir la forma, determinan respectivamente los ángulos de inicio y tangente y la curvatura . En una superficie de un solo parche ( superficie de Bézier ), hay un polo más que los valores de grado de la superficie. Los parches de superficie se pueden fusionar en una sola superficie NURBS; en estos puntos hay líneas de nudos. La cantidad de nudos determinará la influencia de los polos en cada lado y qué tan suave es la transición. La suavidad entre parches, conocida como continuidad , a menudo se menciona en términos de un valor C :
Dos aspectos más importantes son los parámetros U y V. Se trata de valores en la superficie que van de 0 a 1, utilizados en la definición matemática de la superficie y para definir trayectorias en la superficie: por ejemplo, un borde de límite recortado. Tenga en cuenta que no están espaciados proporcionalmente a lo largo de la superficie. Una curva de U constante o V constante se conoce como curva isoperimétrica o línea U (V). En los sistemas CAD, las superficies a menudo se muestran con sus polos de valores U constantes o V constantes conectados entre sí por líneas; estos se conocen como polígonos de control .
A la hora de definir una forma, un factor importante es la continuidad entre superficies: la suavidad con la que se conectan entre sí.
Un ejemplo de cómo el tratamiento de superficies es excelente son los paneles de carrocería de automóviles. No basta con fusionar dos áreas curvas del panel con diferentes radios de curvatura, manteniendo la continuidad tangencial (es decir, que la superficie fusionada no cambie de dirección de repente, sino de manera suave). Deben tener una tasa continua de cambio de curvatura entre las dos secciones, o de lo contrario sus reflejos aparecerán desconectados.
La continuidad se define utilizando los términos:
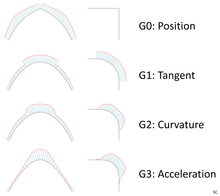
Para lograr una superficie NURBS o Bézier de alta calidad, generalmente se utilizan grados de 5 o más.