El análisis de frecuencia acumulada es el análisis de la frecuencia de ocurrencia de valores de un fenómeno menores que un valor de referencia. El fenómeno puede depender del tiempo o del espacio. La frecuencia acumulada también se llama frecuencia de no excedencia .
El análisis de frecuencia acumulada se realiza para obtener información sobre la frecuencia con la que un determinado fenómeno (característica) está por debajo de un determinado valor. Esto puede ayudar a describir o explicar una situación en la que está involucrado el fenómeno, o en la planificación de intervenciones, por ejemplo en la protección contra inundaciones. [1]
Esta técnica estadística se puede utilizar para ver la probabilidad de que un evento como una inundación vuelva a ocurrir en el futuro, en función de la frecuencia con la que ocurrió en el pasado. Se puede adaptar para provocar cosas como el cambio climático que provoca inviernos más húmedos y veranos más secos.
El análisis de frecuencia [2] es el análisis de la frecuencia con la que ocurre un fenómeno observado en un rango determinado.
El análisis de frecuencia se aplica a un registro de longitud N de datos observados X 1 , X 2 , X 3 . . . X N sobre un fenómeno variable X . El registro puede depender del tiempo (por ejemplo, la precipitación medida en un lugar) o del espacio (por ejemplo, el rendimiento de los cultivos en un área), o de otra manera.
La frecuencia acumulada M Xr de un valor de referencia Xr es la frecuencia con la cual los valores observados X son menores o iguales a Xr .
La frecuencia acumulada relativa Fc se puede calcular a partir de:
donde N es el número de datos
Brevemente esta expresión se puede observar como:
Cuando Xr = X min , donde X min es el único valor mínimo observado, se encuentra que Fc = 1/ N , porque M = 1 . Por otro lado, cuando Xr = X max , donde X max es el único valor máximo observado, se encuentra que Fc = 1 , porque M = N . Por lo tanto, cuando Fc = 1 esto significa que Xr es un valor por el cual todos los datos son menores o iguales a Xr .
En porcentaje la ecuación dice:
La probabilidad acumulada Pc de X de ser menor o igual que Xr se puede estimar de varias maneras sobre la base de la frecuencia acumulada M.
Una forma es utilizar la frecuencia acumulada relativa Fc como estimación.
Otra forma es tener en cuenta la posibilidad de que, en casos raros, X pueda asumir valores mayores que el máximo observado Xmax . Esto se puede hacer dividiendo la frecuencia acumulada M por N +1 en lugar de N. La estimación entonces se convierte en:
También existen otras propuestas para el denominador (ver trazado de posiciones ).
La estimación de la probabilidad se facilita clasificando los datos.
Cuando los datos observados de X están ordenados en orden ascendente ( X 1 ≤ X 2 ≤ X 3 ≤ ⋯ ≤ X N , el mínimo primero y el máximo último), y Ri es el número de rango de la observación Xi , donde el adfijo i indica el número de serie en el rango de datos ascendentes, entonces la probabilidad acumulada puede estimarse mediante:
Cuando, por otro lado, los datos observados de X están ordenados en orden descendente , el máximo primero y el mínimo al final, y Rj es el número de rango de la observación Xj , la probabilidad acumulada puede estimarse mediante:

Para presentar la distribución de frecuencia acumulativa como una ecuación matemática continua en lugar de un conjunto discreto de datos, se puede intentar ajustar la distribución de frecuencia acumulativa a una distribución de probabilidad acumulativa conocida. [2] [3]
Si tiene éxito, la ecuación conocida es suficiente para informar la distribución de frecuencia y no será necesaria una tabla de datos. Además, la ecuación ayuda a la interpolación y extrapolación. Sin embargo, se debe tener cuidado al extrapolar una distribución de frecuencia acumulada, porque esto puede ser una fuente de errores. Un posible error es que la distribución de frecuencias ya no sigue la distribución de probabilidad seleccionada más allá del rango de los datos observados.
Cualquier ecuación que dé el valor 1 cuando se integra desde un límite inferior a un límite superior que concuerde bien con el rango de datos, se puede utilizar como distribución de probabilidad para el ajuste. Una muestra de distribuciones de probabilidad que pueden usarse se puede encontrar en Distribuciones de probabilidad .
Las distribuciones de probabilidad se pueden ajustar mediante varios métodos, [2] por ejemplo:
Aplicación de ambos tipos de métodos utilizando por ejemplo
a menudo muestra que varias distribuciones se ajustan bien a los datos y no producen resultados significativamente diferentes, mientras que las diferencias entre ellas pueden ser pequeñas en comparación con la amplitud del intervalo de confianza. [2] Esto ilustra que puede ser difícil determinar qué distribución da mejores resultados. Por ejemplo, conjuntos de datos distribuidos aproximadamente normalmente se pueden ajustar a un gran número de distribuciones de probabilidad diferentes. [4] mientras que las distribuciones sesgadas negativamente se pueden ajustar a distribuciones de Gumbel cuadradas normales y reflejadas. [5]

A veces es posible ajustar un tipo de distribución de probabilidad a la parte inferior del rango de datos y otro tipo a la parte superior, separados por un punto de interrupción, con lo que se mejora el ajuste general.
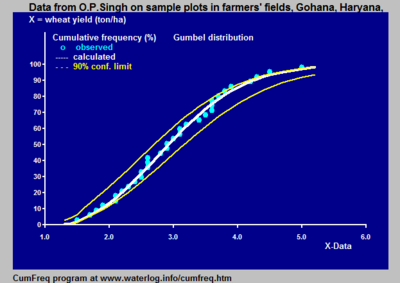
La figura ofrece un ejemplo de una introducción útil de dicha distribución discontinua para los datos de precipitaciones en el norte de Perú, donde el clima está sujeto al comportamiento de la corriente de El Niño del Océano Pacífico . Cuando el Niño se extiende hacia el sur de Ecuador y entra al océano a lo largo de la costa de Perú, el clima en el norte de Perú se vuelve tropical y húmedo. Cuando el Niño no llega al Perú, el clima es semiárido. Por esta razón, las precipitaciones más elevadas siguen una distribución de frecuencia diferente a la de las precipitaciones más bajas. [6]
Cuando una distribución de frecuencia acumulada se deriva de un registro de datos, se puede cuestionar si se puede utilizar para predicciones. [7] Por ejemplo, dada una distribución de las descargas de un río para los años 1950-2000, ¿se puede utilizar esta distribución para predecir con qué frecuencia se excederá la descarga de un determinado río en los años 2000-50? La respuesta es sí, siempre que las condiciones ambientales no cambien. Si las condiciones ambientales cambian, como alteraciones en la infraestructura de la cuenca del río o en el patrón de precipitaciones debido a cambios climáticos, la predicción basada en el registro histórico está sujeta a un error sistemático . Incluso cuando no hay un error sistemático, puede haber un error aleatorio , porque por casualidad las descargas observadas durante 1950 - 2000 pueden haber sido mayores o menores de lo normal, mientras que, por otro lado, las descargas entre 2000 y 2050 pueden ser menores. o superior a lo normal. Las cuestiones relacionadas con esto se han explorado en el libro El cisne negro .

La teoría de la probabilidad puede ayudar a estimar el rango en el que puede encontrarse el error aleatorio. En el caso de la frecuencia acumulada sólo hay dos posibilidades: se supera un determinado valor de referencia X o no se supera. La suma de la frecuencia de superación y la frecuencia acumulada es 1 o 100%. Por lo tanto, la distribución binomial se puede utilizar para estimar el rango del error aleatorio.
Según la teoría normal, la distribución binomial se puede aproximar y para N grandes desviaciones estándar, Sd se puede calcular de la siguiente manera:
donde Pc es la probabilidad acumulada y N es el número de datos. Se ve que la desviación estándar Sd se reduce a medida que aumenta el número de observaciones N.
La determinación del intervalo de confianza de Pc hace uso de la prueba t de Student ( t ). El valor de t depende del número de datos y del nivel de confianza de la estimación del intervalo de confianza. Luego, los límites de confianza inferior ( L ) y superior ( U ) de Pc en una distribución simétrica se encuentran a partir de:
Esto se conoce como intervalo de Wald . [8] Sin embargo, la distribución binomial solo es simétrica alrededor de la media cuando Pc = 0,5 , pero se vuelve asimétrica y cada vez más sesgada cuando Pc se aproxima a 0 o 1. Por lo tanto, por aproximación, Pc y 1− Pc pueden usarse como peso. factores en la asignación de t.Sd a L y U :
donde se puede observar que estas expresiones para Pc = 0.5 son las mismas que las anteriores.

La probabilidad acumulada Pc también puede denominarse probabilidad de no excedencia . La probabilidad de exceder Pe (también llamada función de supervivencia ) se encuentra a partir de:
El período de retorno T se define como:
e indica el número esperado de observaciones que deben realizarse nuevamente para encontrar el valor de la variable en estudio mayor que el valor utilizado para T .
Los límites de confianza superior ( T U ) e inferior ( T L ) de los períodos de retorno se pueden encontrar respectivamente como:
Para valores extremos de la variable en estudio, U es cercano a 1 y pequeños cambios en U originan grandes cambios en T U . Por tanto, el período de retorno estimado de los valores extremos está sujeto a un gran error aleatorio. Además, los intervalos de confianza encontrados se cumplen para una predicción a largo plazo. Para predicciones a corto plazo, los intervalos de confianza U − L y T U − T L pueden en realidad ser más amplios. Junto con la certeza limitada (menos del 100%) utilizada en la prueba t , esto explica por qué, por ejemplo, una lluvia de 100 años podría ocurrir dos veces en 10 años.

La noción estricta de período de retorno en realidad sólo tiene significado cuando se trata de un fenómeno que depende del tiempo, como la lluvia puntual. El período de devolución corresponde entonces al tiempo de espera previsto hasta que vuelva a producirse el exceso. El período de retorno tiene la misma dimensión que el tiempo para el cual cada observación es representativa. Por ejemplo, cuando las observaciones se refieren a precipitaciones diarias, el período de retorno se expresa en días y, para las precipitaciones anuales, en años.
La figura muestra la variación que puede ocurrir al obtener muestras de una variable que sigue una determinada distribución de probabilidad. Los datos fueron proporcionados por Benson. [1]
El cinturón de confianza alrededor de una curva experimental de frecuencia acumulada o período de retorno da una impresión de la región en la que se puede encontrar la verdadera distribución.
Además, aclara que la distribución de probabilidad que mejor se ajusta encontrada experimentalmente puede desviarse de la distribución real.

Los datos observados se pueden organizar en clases o grupos con número de serie k . Cada grupo tiene un límite inferior ( L k ) y un límite superior ( U k ). Cuando la clase ( k ) contiene m k datos y el número total de datos es N , entonces la frecuencia relativa de clase o grupo se encuentra a partir de:
o brevemente:
o en porcentaje:
La presentación de todas las frecuencias de clase da una distribución de frecuencia o histograma . Los histogramas, incluso cuando se elaboran a partir del mismo registro, son diferentes para diferentes límites de clase.
El histograma también se puede derivar de la distribución de probabilidad acumulada ajustada:
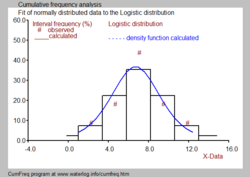
Puede haber una diferencia entre Fg k y Pg k debido a las desviaciones de los datos observados de la distribución ajustada (ver figura azul).
A menudo se desea combinar el histograma con una función de densidad de probabilidad como se muestra en la imagen en blanco y negro.