Un filtro de elementos distribuidos es un filtro electrónico en el que la capacitancia , la inductancia y la resistencia (los elementos del circuito) no están localizados en capacitores , inductores y resistores discretos como en los filtros convencionales. Su propósito es permitir que pase un rango de frecuencias de señal , pero bloquear otras. Los filtros convencionales se construyen a partir de inductores y capacitores, y los circuitos así construidos se describen mediante el modelo de elementos concentrados , que considera que cada elemento está "agrupado" en un lugar. Ese modelo es conceptualmente simple, pero se vuelve cada vez menos confiable a medida que aumenta la frecuencia de la señal o, equivalentemente, a medida que disminuye la longitud de onda . El modelo de elementos distribuidos se aplica a todas las frecuencias y se utiliza en la teoría de líneas de transmisión ; muchos componentes de elementos distribuidos están hechos de longitudes cortas de línea de transmisión. En la visión distribuida de los circuitos, los elementos se distribuyen a lo largo de la longitud de los conductores y están inextricablemente mezclados. El diseño de los filtros suele estar centrado únicamente en la inductancia y la capacitancia, pero debido a esta mezcla de elementos no se los puede tratar como condensadores e inductores "agrupados" separados. No existe una frecuencia precisa por encima de la cual se deban utilizar los filtros de elementos distribuidos, pero se los asocia especialmente con la banda de microondas (longitud de onda inferior a un metro).
Los filtros de elementos distribuidos se utilizan en muchas de las mismas aplicaciones que los filtros de elementos concentrados, como la selectividad del canal de radio, la limitación de banda del ruido y la multiplexación de muchas señales en un canal. Los filtros de elementos distribuidos se pueden construir para tener cualquiera de las formas de banda posibles con elementos concentrados ( paso bajo , paso banda , etc.) con la excepción del paso alto , que generalmente solo se aproxima. Todas las clases de filtros utilizadas en diseños de elementos concentrados ( Butterworth , Chebyshev , etc.) se pueden implementar utilizando un enfoque de elementos distribuidos.
Existen muchas formas de componentes que se utilizan para construir filtros de elementos distribuidos, pero todos tienen la propiedad común de provocar una discontinuidad en la línea de transmisión. Estas discontinuidades presentan una impedancia reactiva a un frente de onda que viaja por la línea, y estas reactancias se pueden elegir por diseño para que sirvan como aproximaciones para inductores , capacitores o resonadores concentrados , según lo requiera el filtro. [4]
El desarrollo de filtros de elementos distribuidos fue impulsado por la necesidad militar de contar con radares y contramedidas electrónicas durante la Segunda Guerra Mundial. Los filtros analógicos de elementos agrupados se habían desarrollado mucho antes, pero estos nuevos sistemas militares operaban en frecuencias de microondas y se necesitaban nuevos diseños de filtros. Cuando terminó la guerra, la tecnología encontró aplicaciones en los enlaces de microondas utilizados por las compañías telefónicas y otras organizaciones con grandes redes de comunicación fija, como las emisoras de televisión. Hoy en día, la tecnología se puede encontrar en varios artículos de consumo producidos en masa, como los convertidores (la figura 1 muestra un ejemplo) utilizados con antenas parabólicas de televisión .

Los filtros de elementos distribuidos se utilizan principalmente en frecuencias superiores a la banda VHF (muy alta frecuencia) (30 a 300 MHz ). En estas frecuencias, la longitud física de los componentes pasivos es una fracción significativa de la longitud de onda de la frecuencia de funcionamiento, y resulta difícil utilizar el modelo de elementos agrupados convencional . El punto exacto en el que se hace necesario el modelado de elementos distribuidos depende del diseño particular que se esté considerando. Una regla general común es aplicar el modelado de elementos distribuidos cuando las dimensiones de los componentes son mayores que 0,1λ. La creciente miniaturización de la electrónica ha significado que los diseños de circuitos se están volviendo cada vez más pequeños en comparación con λ. Las frecuencias más allá de las cuales se hace necesario un enfoque de elementos distribuidos para el diseño de filtros son cada vez más altas como resultado de estos avances. Por otro lado, las dimensiones de la estructura de la antena suelen ser comparables a λ en todas las bandas de frecuencia y requieren el modelo de elementos distribuidos. [5]
La diferencia de comportamiento más notable entre un filtro de elementos distribuidos y su aproximación de elementos concentrados es que el primero tendrá múltiples réplicas de banda de paso de la banda de paso del prototipo de elementos concentrados , porque las características de transferencia de la línea de transmisión se repiten a intervalos armónicos. Estas bandas de paso espurias son indeseables en la mayoría de los casos. [6]
Para mayor claridad en la presentación, los diagramas de este artículo se han dibujado con los componentes implementados en formato stripline . Esto no implica una preferencia de la industria, aunque los formatos de líneas de transmisión planas (es decir, formatos donde los conductores consisten en tiras planas) son populares porque se pueden implementar utilizando técnicas establecidas de fabricación de placas de circuito impreso . Las estructuras mostradas también se pueden implementar utilizando técnicas de microstrip o stripline enterrado (con los ajustes adecuados a las dimensiones) y se pueden adaptar a cables coaxiales , conductores gemelos y guías de onda , aunque algunas estructuras son más adecuadas para algunas implementaciones que otras. Las implementaciones de cable abierto, por ejemplo, de varias estructuras se muestran en la segunda columna de la figura 3 y se pueden encontrar equivalentes de cable abierto para la mayoría de las otras estructuras de stripline. Las líneas de transmisión planas también se utilizan en diseños de circuitos integrados . [7]
El desarrollo de filtros de elementos distribuidos comenzó en los años anteriores a la Segunda Guerra Mundial. Warren P. Mason fundó el campo de los circuitos de elementos distribuidos . [8] Mason y Sykes publicaron un importante artículo sobre el tema en 1937. [9] Mason había presentado una patente [10] mucho antes, en 1927, y esa patente puede contener el primer diseño eléctrico publicado que se aleja del análisis de elementos agrupados. [11] El trabajo de Mason y Sykes se centró en los formatos de cable coaxial y pares de cables balanceados: las tecnologías planares aún no se utilizaban. Durante los años de guerra se llevó a cabo gran parte del desarrollo impulsado por las necesidades de filtrado del radar y las contramedidas electrónicas . Una buena parte de esto se realizó en el Laboratorio de Radiación del MIT , [12] pero también participaron otros laboratorios de los EE. UU. y el Reino Unido. [13] [14]
Se necesitaron algunos avances importantes en la teoría de redes antes de que los filtros pudieran ir más allá de los diseños de tiempos de guerra. Uno de ellos fue la teoría de líneas conmensuradas de Paul Richards . [15] Las líneas conmensuradas son redes en las que todos los elementos tienen la misma longitud (o en algunos casos múltiplos de la longitud unitaria), aunque pueden diferir en otras dimensiones para dar lugar a diferentes impedancias características. La transformación de Richards permite tomar un diseño de elementos concentrados "tal como está" y transformarlo directamente en un diseño de elementos distribuidos utilizando una ecuación de transformación muy simple. [16]
La dificultad de la transformación de Richards desde el punto de vista de la construcción de filtros prácticos era que el diseño de elementos distribuidos resultante incluía invariablemente elementos conectados en serie . Esto no era posible de implementar en tecnologías planares y a menudo resultaba inconveniente en otras tecnologías. Este problema fue resuelto por K. Kuroda, que utilizó transformadores de impedancia para eliminar los elementos en serie. Publicó un conjunto de transformaciones conocidas como las identidades de Kuroda en 1955, pero su trabajo fue escrito en japonés y pasaron varios años antes de que sus ideas se incorporaran a la literatura en idioma inglés. [17]
Después de la guerra, una importante línea de investigación fue tratar de aumentar el ancho de banda de diseño de los filtros de banda ancha. El enfoque utilizado en ese momento (y todavía en uso hoy) fue comenzar con un prototipo de filtro de elemento concentrado y, a través de varias transformaciones, llegar al filtro deseado en forma de elemento distribuido. Este enfoque parecía estar estancado en un Q mínimo de cinco (consulte Filtros de paso de banda a continuación para obtener una explicación de Q ). En 1957, Leo Young en el Stanford Research Institute publicó un método para diseñar filtros que comenzaba con un prototipo de elemento distribuido. [18] Este prototipo se basaba en transformadores de impedancia de cuarto de onda y podía producir diseños con anchos de banda de hasta una octava , correspondientes a un Q de aproximadamente 1,3. Algunos de los procedimientos de Young en ese artículo eran empíricos, pero más tarde, [19] se publicaron soluciones exactas. El artículo de Young aborda específicamente los resonadores de cavidad acoplados directamente, pero el procedimiento se puede aplicar igualmente a otros tipos de resonadores acoplados directamente, como los que se encuentran en las tecnologías planares modernas y se ilustran en este artículo. El filtro de espacio capacitivo (figura 8) y el filtro de líneas acopladas en paralelo (figura 9) son ejemplos de resonadores acoplados directamente. [16]
 representa una correa que pasa a través del tablero y hace conexión con el plano de tierra que se encuentra debajo.
representa una correa que pasa a través del tablero y hace conexión con el plano de tierra que se encuentra debajo.La introducción de tecnologías planares impresas simplificó enormemente la fabricación de muchos componentes de microondas, incluidos los filtros, y luego se hicieron posibles los circuitos integrados de microondas. No se sabe cuándo se originaron las líneas de transmisión planares, pero se registraron experimentos con ellas ya en 1936. [20] Sin embargo, se sabe quién inventó la línea de banda impresa; fue Robert M. Barrett, quien publicó la idea en 1951. [21] Esto se popularizó rápidamente y la línea de banda de Barrett pronto tuvo una feroz competencia comercial con los formatos planares rivales, especialmente triplante y microbanda . El término genérico stripline en el uso moderno generalmente se refiere a la forma conocida entonces como triplante . [22]
Los primeros filtros resonadores acoplados directamente con línea de banda estaban acoplados en los extremos, pero la longitud se redujo y la compacidad aumentó sucesivamente con la introducción de filtros de línea acoplados en paralelo, [23] filtros interdigitales, [24] y filtros de línea de peine. [25] Gran parte de este trabajo fue publicado por el grupo de Stanford dirigido por George Matthaei, y también incluyendo a Leo Young mencionado anteriormente, en un libro histórico que todavía hoy sirve como referencia para diseñadores de circuitos. [26] [27] El filtro de horquilla se describió por primera vez en 1972. [28] [29] En la década de 1970, se habían descrito la mayoría de las topologías de filtro de uso común en la actualidad. [30] La investigación más reciente se ha concentrado en clases matemáticas nuevas o variantes de los filtros, como pseudoelípticos , mientras se siguen utilizando las mismas topologías básicas, o con tecnologías de implementación alternativas como stripline suspendido y finline . [31]
La primera aplicación no militar de los filtros de elementos distribuidos fue en los enlaces de microondas que utilizaban las empresas de telecomunicaciones para proporcionar la columna vertebral de sus redes. Estos enlaces también los utilizaban otras industrias con grandes redes fijas, en particular las emisoras de televisión. [32] Estas aplicaciones formaban parte de grandes programas de inversión de capital. Sin embargo, la fabricación en serie hizo que la tecnología fuera lo suficientemente barata como para incorporarla en los sistemas domésticos de televisión por satélite . [33] Una aplicación emergente es la de los filtros superconductores para su uso en las estaciones base celulares operadas por las compañías de telefonía móvil. [34]
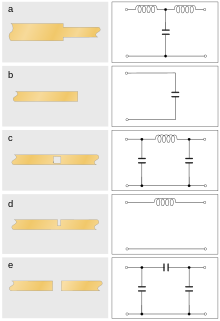
La estructura más simple que se puede implementar es un paso en la impedancia característica de la línea, que introduce una discontinuidad en las características de transmisión. Esto se hace en tecnologías planares mediante un cambio en el ancho de la línea de transmisión. La figura 4(a) muestra un aumento en la impedancia (las líneas más estrechas tienen mayor impedancia). Un paso hacia abajo en la impedancia sería la imagen especular de la figura 4(a). La discontinuidad se puede representar aproximadamente como un inductor en serie, o más exactamente, como un circuito T de paso bajo como se muestra en la figura 4(a). [35] Las discontinuidades múltiples a menudo se acoplan con transformadores de impedancia para producir un filtro de orden superior . Estos transformadores de impedancia pueden ser solo una longitud corta (a menudo λ/4) de línea de transmisión. Estas estructuras compuestas pueden implementar cualquiera de las familias de filtros ( Butterworth , Chebyshev , etc.) aproximando la función de transferencia racional del filtro de elementos concentrados correspondiente. Esta correspondencia no es exacta, ya que los circuitos de elementos distribuidos no pueden ser racionales y es la razón fundamental de la divergencia del comportamiento de los elementos concentrados y los elementos distribuidos. Los transformadores de impedancia también se utilizan en mezclas híbridas de filtros de elementos concentrados y distribuidos (las denominadas estructuras semiconcentradas). [36]
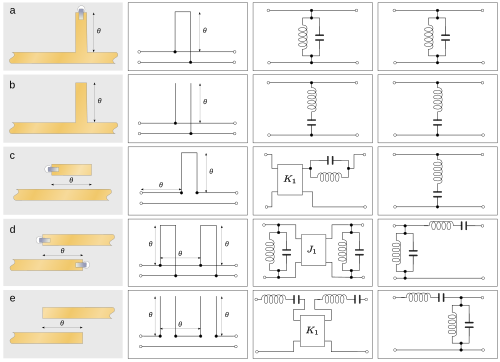
Otro componente muy común de los filtros de elementos distribuidos es el stub . En un rango estrecho de frecuencias, un stub se puede utilizar como un condensador o un inductor (su impedancia está determinada por su longitud), pero en una banda ancha se comporta como un resonador. Los stubs de cortocircuito, nominalmente de un cuarto de longitud de onda (figura 3(a)) se comportan como antirresonadores LC en derivación , y un stub de circuito abierto nominalmente de un cuarto de longitud de onda (figura 3(b)) se comporta como un resonador LC en serie . Los stubs también se pueden utilizar junto con transformadores de impedancia para construir filtros más complejos y, como se esperaría de su naturaleza resonante, son más útiles en aplicaciones de paso de banda. [39] Si bien los stubs de circuito abierto son más fáciles de fabricar en tecnologías planares, tienen el inconveniente de que la terminación se desvía significativamente de un circuito abierto ideal (ver figura 4(b)), lo que a menudo conduce a una preferencia por stubs de cortocircuito (uno siempre se puede usar en lugar del otro agregando o restando λ/4 a la longitud). [35]
Un resonador helicoidal es similar a un stub, en el sentido de que requiere un modelo de elementos distribuidos para representarlo, pero en realidad se construye utilizando elementos concentrados. Se construyen en un formato no plano y consisten en una bobina de alambre, sobre un núcleo y una matriz, y conectados solo en un extremo. El dispositivo suele estar en una lata blindada con un orificio en la parte superior para ajustar el núcleo. A menudo se verá físicamente muy similar a los resonadores LC concentrados utilizados para un propósito similar. Son más útiles en las bandas superiores de VHF y UHF inferiores , mientras que los stubs se aplican con más frecuencia en las bandas superiores de UHF y SHF . [40]
Las líneas acopladas (figuras 3(ce)) también se pueden utilizar como elementos de filtro; al igual que los stubs, pueden actuar como resonadores y, asimismo, terminarse en cortocircuito o circuito abierto. Las líneas acopladas tienden a preferirse en tecnologías planares, donde son fáciles de implementar, mientras que los stubs tienden a preferirse en otros lugares. Implementar un verdadero circuito abierto en tecnología planar no es factible debido al efecto dieléctrico del sustrato que siempre asegurará que el circuito equivalente contenga una capacitancia en derivación. A pesar de esto, los circuitos abiertos se utilizan a menudo en formatos planares en lugar de los cortocircuitos porque son más fáciles de implementar. Numerosos tipos de elementos se pueden clasificar como líneas acopladas y en las figuras se muestra una selección de los más comunes. [41]
En las figuras 3 y 4 se muestran algunas estructuras comunes, junto con sus contrapartes de elementos concentrados. Estas aproximaciones de elementos concentrados no deben tomarse como circuitos equivalentes, sino más bien como una guía para el comportamiento de los elementos distribuidos en un cierto rango de frecuencias. Las figuras 3(a) y 3(b) muestran un stub de cortocircuito y circuito abierto, respectivamente. Cuando la longitud del stub es λ/4, estos se comportan, respectivamente, como antirresonadores y resonadores y, por lo tanto, son útiles, respectivamente, como elementos en filtros de paso de banda y de eliminación de banda . La figura 3(c) muestra una línea en cortocircuito acoplada a la línea principal. Esto también se comporta como un resonador, pero se usa comúnmente en aplicaciones de filtro de paso bajo con la frecuencia de resonancia muy fuera de la banda de interés. Las figuras 3(d) y 3(e) muestran estructuras de línea acopladas que son útiles en filtros de paso de banda. Las estructuras de las figuras 3(c) y 3(e) tienen circuitos equivalentes que involucran stubs colocados en serie con la línea. Una topología de este tipo es fácil de implementar en circuitos de cable abierto, pero no con una tecnología planar. Por lo tanto, estas dos estructuras son útiles para implementar un elemento en serie equivalente. [42]


Un filtro de paso bajo se puede implementar de forma bastante directa a partir de un prototipo de elemento concentrado de topología de escalera con el filtro de impedancia escalonada que se muestra en la figura 5. Esto también se denomina diseño de líneas en cascada . El filtro consta de secciones alternas de líneas de alta impedancia y baja impedancia que corresponden a los inductores en serie y los condensadores en derivación en la implementación de elemento concentrado. Los filtros de paso bajo se utilizan comúnmente para alimentar polarización de corriente continua (CC) a componentes activos. Los filtros destinados a esta aplicación a veces se denominan estranguladores . En tales casos, cada elemento del filtro tiene una longitud de λ/4 (donde λ es la longitud de onda de la señal de la línea principal que se bloqueará para que no se transmita a la fuente de CC) y las secciones de alta impedancia de la línea se hacen tan estrechas como lo permita la tecnología de fabricación para maximizar la inductancia. [43] Se pueden agregar secciones adicionales según sea necesario para el rendimiento del filtro, tal como se haría para la contraparte de elemento concentrado. Además de la forma plana mostrada, esta estructura es particularmente adecuada para implementaciones coaxiales con discos alternados de metal y aislante enroscados en el conductor central. [44] [45] [46]

En la figura 6 se presenta un ejemplo más complejo de diseño de impedancia escalonada. Nuevamente, se utilizan líneas estrechas para implementar inductores y líneas anchas corresponden a capacitores, pero en este caso, la contraparte de elementos concentrados tiene resonadores conectados en derivación a través de la línea principal. Esta topología se puede utilizar para diseñar filtros elípticos o filtros Chebyshev con polos de atenuación en la banda de supresión . Sin embargo, calcular los valores de los componentes para estas estructuras es un proceso complicado y ha llevado a los diseñadores a menudo a optar por implementarlos como filtros derivados de m , que funcionan bien y son mucho más fáciles de calcular. El propósito de incorporar resonadores es mejorar el rechazo de la banda de supresión . Sin embargo, más allá de la frecuencia de resonancia del resonador de frecuencia más alta, el rechazo de la banda de supresión comienza a deteriorarse a medida que los resonadores se mueven hacia el circuito abierto. Por esta razón, los filtros construidos con este diseño a menudo tienen un capacitor adicional de impedancia escalonada simple como elemento final del filtro. [47] Esto también asegura un buen rechazo a alta frecuencia. [48] [49] [50]
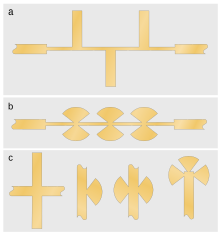
Otra técnica común de diseño de paso bajo es implementar los condensadores en derivación como stubs con la frecuencia de resonancia establecida por encima de la frecuencia de operación, de modo que la impedancia del stub sea capacitiva en la banda de paso. Esta implementación tiene una contraparte de elementos concentrados de una forma general similar al filtro de la figura 6. Cuando el espacio lo permite, los stubs se pueden colocar en lados alternos de la línea principal, como se muestra en la figura 7(a). El propósito de esto es evitar el acoplamiento entre stubs adyacentes que perjudica el rendimiento del filtro al alterar la respuesta de frecuencia. Sin embargo, una estructura con todos los stubs en el mismo lado sigue siendo un diseño válido. Si se requiere que el stub sea una línea de impedancia muy baja, el stub puede ser inconvenientemente ancho. En estos casos, una posible solución es conectar dos stubs más estrechos en paralelo. Es decir, cada posición de stub tiene un stub en ambos lados de la línea. Una desventaja de esta topología es que son posibles modos resonantes transversales adicionales a lo largo de la longitud λ/2 de la línea formada por los dos ramales juntos. Para un diseño de estrangulamiento, el requisito es simplemente hacer que la capacitancia sea lo más grande posible, para lo cual se puede usar el ancho máximo de ramal de λ/4 con ramales en paralelo en ambos lados de la línea principal. El filtro resultante se ve bastante similar al filtro de impedancia escalonada de la figura 5, pero se ha diseñado sobre principios completamente diferentes. [43] Una dificultad con el uso de ramales tan anchos es que el punto en el que se conectan a la línea principal está mal definido. Un ramal que es estrecho en comparación con λ se puede tomar como conectado en su línea central y los cálculos basados en esa suposición predecirán con precisión la respuesta del filtro. Sin embargo, para un ramal ancho, los cálculos que suponen que la rama lateral está conectada en un punto definido en la línea principal conducen a imprecisiones, ya que este ya no es un buen modelo del patrón de transmisión. Una solución a esta dificultad es utilizar conectores radiales en lugar de conectores lineales. Un par de conectores radiales en paralelo (uno a cada lado de la línea principal) se denomina conector mariposa (véase la figura 7(b)). Un grupo de tres conectores radiales en paralelo, que se puede lograr al final de una línea, se denomina conector en forma de trébol. [51] [52]
Se puede construir un filtro de paso de banda utilizando cualquier elemento que pueda resonar. Los filtros que utilizan stubs se pueden convertir claramente en filtros de paso de banda; existen muchas otras estructuras posibles, algunas de las cuales se presentan a continuación.
Un parámetro importante cuando se habla de filtros de paso de banda es el ancho de banda fraccional. Este se define como la relación entre el ancho de banda y la frecuencia central geométrica. La inversa de esta cantidad se denomina factor Q , Q. Si ω 1 y ω 2 son las frecuencias de los bordes de la banda de paso, entonces: [53]

La estructura de brecha capacitiva consiste en secciones de línea de aproximadamente λ/2 de longitud que actúan como resonadores y están acopladas "de extremo a extremo" por brechas en la línea de transmisión. Es particularmente adecuada para formatos planos, se implementa fácilmente con tecnología de circuitos impresos y tiene la ventaja de no ocupar más espacio que una línea de transmisión simple. La limitación de esta topología es que el rendimiento (en particular la pérdida de inserción ) se deteriora con el aumento del ancho de banda fraccional, y no se obtienen resultados aceptables con un Q menor que aproximadamente 5. Una dificultad adicional con la producción de diseños de Q bajo es que se requiere que el ancho de la brecha sea menor para anchos de banda fraccionales más amplios. El ancho mínimo de las brechas, como el ancho mínimo de las pistas , está limitado por la resolución de la tecnología de impresión. [46] [54]

Las líneas acopladas en paralelo son otra topología popular para placas impresas, para las cuales las líneas de circuito abierto son las más simples de implementar ya que la fabricación consiste en nada más que la pista impresa. El diseño consiste en una fila de resonadores λ/2 paralelos, pero acoplados solo sobre λ/4 a cada uno de los resonadores vecinos, formando así una línea escalonada como se muestra en la figura 9. Con este filtro son posibles anchos de banda fraccionales más amplios que con el filtro de espacio capacitivo, pero surge un problema similar en las placas impresas ya que la pérdida dieléctrica reduce el Q . Las líneas de Q más bajas requieren un acoplamiento más ajustado y espacios más pequeños entre ellas, lo que está limitado por la precisión del proceso de impresión. Una solución a este problema es imprimir la pista en múltiples capas con líneas adyacentes superpuestas pero no en contacto porque están en capas diferentes. De esta manera, las líneas se pueden acoplar a lo ancho, lo que da como resultado un acoplamiento mucho más fuerte que cuando están de borde a borde, y se hace posible un espacio más grande para el mismo rendimiento. [55]

Para otras tecnologías (no impresas), pueden preferirse las líneas de cortocircuito, ya que el cortocircuito proporciona un punto de conexión mecánico para la línea y no se requieren aisladores dieléctricos reductores de Q para el soporte mecánico. Aparte de razones mecánicas y de ensamblaje, hay poca preferencia por líneas acopladas en circuito abierto sobre líneas acopladas en cortocircuito. Ambas estructuras pueden lograr la misma gama de implementaciones de filtros con el mismo rendimiento eléctrico. Ambos tipos de filtros acoplados en paralelo, en teoría, no tienen bandas de paso espurias al doble de la frecuencia central como se ve en muchas otras topologías de filtros (por ejemplo, stubs). Sin embargo, la supresión de esta banda de paso espuria requiere un ajuste perfecto de las líneas acopladas, lo que no se logra en la práctica, por lo que inevitablemente hay alguna banda de paso espuria residual en esta frecuencia. [46] [56] [57]

El filtro de horquilla es otra estructura que utiliza líneas acopladas en paralelo. En este caso, cada par de líneas acopladas en paralelo está conectado al par siguiente mediante un enlace corto. Las formas de "U" así formadas dan lugar al nombre de filtro de horquilla . En algunos diseños, el enlace puede ser más largo, lo que da lugar a una horquilla ancha con una acción de transformador de impedancia λ/4 entre secciones. [58] [59]

Las curvas en ángulo que se ven en la figura 10 son comunes en los diseños de líneas de cinta y representan un compromiso entre un ángulo recto agudo, que produce una gran discontinuidad, y una curva suave, que ocupa más área de la placa, que puede estar severamente limitada en algunos productos. Estas curvas se ven a menudo en conectores largos donde de otra manera no podrían caber en el espacio disponible. El circuito equivalente de elementos concentrados de este tipo de discontinuidad es similar a una discontinuidad de impedancia escalonada. [38] Se pueden ver ejemplos de estos conectores en las entradas de polarización de varios componentes en la fotografía que aparece en la parte superior del artículo. [46] [60]


Los filtros interdigitales son otra forma de filtro de línea acoplada. Cada sección de línea tiene una longitud de aproximadamente λ/4 y termina en cortocircuito en un solo extremo, mientras que el otro extremo se deja abierto. El extremo que está en cortocircuito se alterna en cada sección de línea. Esta topología es sencilla de implementar en tecnologías planares, pero también se presta particularmente a un ensamblaje mecánico de líneas fijadas dentro de una caja de metal. Las líneas pueden ser varillas circulares o barras rectangulares, y la interconexión a una línea de formato coaxial es fácil. Al igual que con el filtro de línea acoplado en paralelo, la ventaja de una disposición mecánica que no requiere aisladores para su soporte es que se eliminan las pérdidas dieléctricas. El requisito de espaciado entre líneas no es tan estricto como en la estructura de línea paralela; como tal, se pueden lograr anchos de banda fraccionarios más altos y son posibles valores Q tan bajos como 1,4. [61] [62]
El filtro de línea de peine es similar al filtro interdigital en el sentido de que se presta al montaje mecánico en una caja de metal sin soporte dieléctrico. En el caso del filtro de línea de peine, todas las líneas están cortocircuitadas en el mismo extremo en lugar de en extremos alternos. Los otros extremos están terminados en condensadores a tierra y, en consecuencia, el diseño se clasifica como semiagrupado. La principal ventaja de este diseño es que la banda de supresión superior se puede hacer muy amplia, es decir, libre de bandas de paso espurias en todas las frecuencias de interés. [63]

Como se mencionó anteriormente, los stubs se prestan a diseños de paso de banda. Las formas generales de estos son similares a los filtros stub de paso bajo, excepto que la línea principal ya no es una línea estrecha de alta impedancia. Los diseñadores tienen muchas topologías diferentes de filtros stub para elegir, algunas de las cuales producen respuestas idénticas. Un ejemplo de filtro stub se muestra en la figura 12; consta de una fila de stubs de cortocircuito λ/4 acoplados entre sí por transformadores de impedancia λ/4.
Los stubs en el cuerpo del filtro son stubs dobles en paralelo mientras que los stubs en las secciones finales son solo simples, una disposición que tiene ventajas en la adaptación de impedancia. Los transformadores de impedancia tienen el efecto de transformar la fila de antirresonadores en derivación en una escalera de resonadores en serie y antirresonadores en derivación. Se puede construir un filtro con propiedades similares con stubs de circuito abierto λ/4 colocados en serie con la línea y acoplados entre sí con transformadores de impedancia λ/4, aunque esta estructura no es posible en tecnologías planares. [64]
Otra estructura disponible son los ramales de circuito abierto λ/2 a lo largo de la línea acoplados con transformadores de impedancia λ/4. Esta topología tiene características de paso bajo y paso de banda. Debido a que dejará pasar CC, es posible transmitir voltajes de polarización a componentes activos sin la necesidad de capacitores de bloqueo. Además, dado que no se requieren enlaces de cortocircuito, no se requieren operaciones de ensamblaje que no sean la impresión de la placa cuando se implementa como línea de cinta. Las desventajas son

Konishi describe un filtro de paso de banda de 12 GHz de banda ancha, que utiliza conectores de mariposa de 60° y también tiene una respuesta de paso bajo (se requieren conectores de cortocircuito para evitar dicha respuesta). Como suele suceder con los filtros de elementos distribuidos, la forma de banda en la que se clasifica el filtro depende en gran medida de qué bandas se desean y cuáles se consideran espurias. [66]
Los filtros de paso alto genuinos son difíciles, si no imposibles, de implementar con elementos distribuidos. El enfoque de diseño habitual es comenzar con un diseño de paso de banda, pero hacer que la banda de rechazo superior se produzca a una frecuencia que es tan alta que no tiene interés. Estos filtros se describen como pseudo-paso alto y la banda de rechazo superior se describe como una banda de rechazo vestigial. Incluso las estructuras que parecen tener una topología de paso alto "obvia", como el filtro de brecha capacitivo de la figura 8, resultan ser de paso de banda cuando se considera su comportamiento para longitudes de onda muy cortas. [67]