Filtro Chebyshev

Tipo de filtro analógico o digital

Los filtros Chebyshev son filtros analógicos o digitales que tienen una caída más pronunciada que los filtros Butterworth y tienen ondulación de banda de paso (tipo I) o ondulación de banda de parada (tipo II). Los filtros Chebyshev tienen la propiedad de minimizar el error entre la característica idealizada y la real del filtro en el rango de frecuencia operativa del filtro, ^{[1] [2]} pero lo logran con ondulaciones en la banda de paso. Este tipo de filtro lleva el nombre de Pafnuty Chebyshev porque sus características matemáticas se derivan de los polinomios de Chebyshev . Los filtros Chebyshev de tipo I suelen denominarse "filtros Chebyshev", mientras que los filtros de tipo II suelen denominarse "filtros Chebyshev inversos". ^[3] Debido a la ondulación de la banda de paso inherente a los filtros Chebyshev, para ciertas aplicaciones se prefieren filtros con una respuesta más suave en la banda de paso pero una respuesta más irregular en la banda de parada. ^[4]

Filtros Chebyshev tipo I (filtros Chebyshev)

La respuesta de frecuencia de un filtro de paso bajo Chebyshev tipo I de cuarto orden con ${\displaystyle \varepsilon =1}$

Los filtros Chebyshev tipo I son los tipos más comunes de filtros Chebyshev. La respuesta de ganancia (o amplitud ), en función de la frecuencia angular del filtro de paso bajo de orden th, es igual al valor absoluto de la función de transferencia evaluada en : ${\displaystyle G_{n}(\omega )}$ ${\displaystyle \omega }$ ${\displaystyle n}$ ${\displaystyle H_{n}(s)}$ ${\displaystyle s=j\omega }$

${\displaystyle G_{n}(\omega )=\left|H_{n}(j\omega )\right|={\frac {1}{\sqrt {1+\varepsilon ^{2}T_{n}^{2}(\omega /\omega _{0})}}}}$

donde es el factor de ondulación, es la frecuencia de corte y es un polinomio de Chebyshev de orden ésimo. ${\displaystyle \varepsilon }$ ${\displaystyle \omega _{0}}$ ${\displaystyle T_{n}}$ ${\displaystyle n}$

La banda de paso exhibe un comportamiento equivalente a la ondulación, donde la ondulación está determinada por el factor de ondulación . En la banda de paso, el polinomio de Chebyshev alterna entre -1 y 1, por lo que la ganancia del filtro alterna entre máximos y mínimos en . ${\displaystyle \varepsilon }$ ${\displaystyle G=1}$ ${\displaystyle G=1/{\sqrt {1+\varepsilon ^{2}}}}$

Por tanto, el factor de ondulación ε está relacionado con la ondulación de la banda de paso δ en decibelios mediante:

${\displaystyle \varepsilon ={\sqrt {10^{\delta /10}-1}}.}$

En la frecuencia de corte, la ganancia vuelve a tener el valor pero continúa cayendo en la banda de parada a medida que aumenta la frecuencia. Este comportamiento se muestra en el diagrama de la derecha. La práctica común de definir la frecuencia de corte en −3  dB no suele aplicarse a los filtros Chebyshev; en cambio, el límite se toma como el punto en el que la ganancia cae al valor de la ondulación por última vez. ${\displaystyle \omega _{0}}$ ${\displaystyle 1/{\sqrt {1+\varepsilon ^{2}}}}$

La frecuencia de 3 dB está relacionada con: ${\displaystyle \omega _{H}}$ ${\displaystyle \omega _{0}}$

${\displaystyle \omega _{H}=\omega _{0}\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right).}$

El orden de un filtro Chebyshev es igual al número de componentes reactivos (por ejemplo, inductores ) necesarios para realizar el filtro utilizando electrónica analógica .

Se puede obtener una caída aún más pronunciada si se permite la ondulación en la banda de parada, permitiendo ceros en el eje en el plano complejo. Si bien esto produce una supresión casi infinita en y cerca de estos ceros (limitada por el factor de calidad de los componentes, parásitos y factores relacionados), la supresión general en la banda de parada se reduce. El resultado se denomina filtro elíptico , también conocido como filtro de Cauer. ${\displaystyle \omega }$

Polos y ceros

Registro del valor absoluto de la ganancia de un filtro Chebyshev tipo I de octavo orden en un espacio de frecuencia complejo ( s  =  σ  +  jω ) con ε = 0,1 y . Los puntos blancos son polos y están dispuestos en una elipse con un semieje de 0,3836... en σ y 1,071... en ω. Los polos de la función de transferencia son aquellos polos en el semiplano izquierdo. El negro corresponde a una ganancia de 0,05 o menos, el blanco corresponde a una ganancia de 20 o más. ${\displaystyle \omega _{0}=1}$

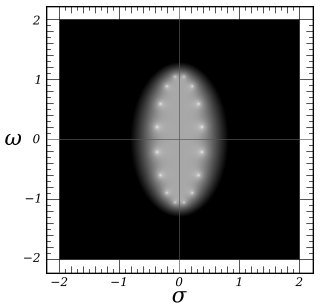
Por simplicidad, se supone que la frecuencia de corte es igual a la unidad. Los polos de la función de ganancia del filtro de Chebyshev son los ceros del denominador de la función de ganancia. Usando la frecuencia compleja , estos ocurren cuando: ${\displaystyle (\omega _{pm})}$ ${\displaystyle s}$

${\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(-js)=0.\,}$

Definir y utilizar la definición trigonométrica de los polinomios de Chebyshev produce: ${\displaystyle -js=\cos(\theta )}$

${\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(\cos(\theta ))=1+\varepsilon ^{2}\cos ^{2}(n\theta )=0.\,}$

Resolviendo para ${\displaystyle \theta }$

${\displaystyle \theta ={\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}}$

donde los múltiples valores de la función arcocoseno se hacen explícitos utilizando el índice entero . Los polos de la función de ganancia de Chebyshev son entonces: ${\displaystyle m}$

${\displaystyle s_{pm}=j\cos(\theta )\,}$

${\displaystyle =j\cos \left({\frac {1}{n}}\arccos \left({\frac {\pm j}{\varepsilon }}\right)+{\frac {m\pi }{n}}\right).}$

Usando las propiedades de las funciones trigonométricas e hiperbólicas, esto se puede escribir en forma explícitamente compleja:

${\displaystyle s_{pm}^{\pm }=\pm \sinh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})}$

${\displaystyle +j\cosh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})}$

dónde  y ${\displaystyle m=1,2,...,n}$

${\displaystyle \theta _{m}={\frac {\pi }{2}}\,{\frac {2m-1}{n}}.}$

Esto puede verse como una ecuación paramétrica y demuestra que los polos se encuentran en una elipse en el espacio centrada en un semieje real de longitud y un semieje imaginario de longitud de ${\displaystyle \theta _{n}}$ ${\displaystyle s}$ ${\displaystyle s=0}$ ${\displaystyle \sinh(\mathrm {arsinh} (1/\varepsilon )/n)}$ ${\displaystyle \cosh(\mathrm {arsinh} (1/\varepsilon )/n).}$

La función de transferencia

La expresión anterior produce los polos de la ganancia . Por cada polo complejo hay otro que es el complejo conjugado, y por cada par de conjugados hay dos más que son los negativos del par. La función de transferencia debe ser estable, de modo que sus polos sean los de la ganancia que tienen partes reales negativas y, por tanto, se encuentran en el semiplano izquierdo del espacio de frecuencias complejo. La función de transferencia entonces viene dada por ${\displaystyle G}$

${\displaystyle H(s)={\frac {1}{2^{n-1}\varepsilon }}\ \prod _{m=1}^{n}{\frac {1}{(s-s_{pm}^{-})}}}$

donde están sólo aquellos polos de la ganancia con signo negativo delante del término real, obtenidos de la ecuación anterior. ${\displaystyle s_{pm}^{-}}$

El retraso del grupo

Ganancia y retardo de grupo de un filtro Chebyshev tipo I de quinto orden con ε = 0,5.

El retardo de grupo se define como la derivada de la fase con respecto a la frecuencia angular y es una medida de la distorsión en la señal introducida por las diferencias de fase para diferentes frecuencias.

${\displaystyle \tau _{g}=-{\frac {d}{d\omega }}\arg(H(j\omega ))}$

La ganancia y el retardo de grupo para un filtro Chebyshev tipo I de quinto orden con ε = 0,5 se representan en el gráfico de la izquierda. Se puede observar que hay ondulaciones en la ganancia y el retardo de grupo en la banda de paso pero no en la banda de parada.

Incluso modificaciones de pedidos

Incluso los filtros Chebyshev de orden implementados con elementos pasivos, típicamente inductores, condensadores y líneas de transmisión, con terminaciones de igual valor en cada lado, no se pueden implementar con la función de transferencia tradicional de Chebyshev. Esto se debe a la incapacidad física para acomodar los ceros de reflexión de Chebyshev de orden par que dan como resultado una matriz de dispersión S12 mayor que 1. Si no es factible diseñar el filtro con una de las terminaciones aumentada o disminuida, entonces la función de transferencia de Chebyshev debe modificarse para mover la reflexión de orden par más baja de cero a cero mientras se mantiene la respuesta de ondulación equivalente de la banda de paso.

La modificación necesaria implica mapear cada polo de la función de transferencia de Chebyshev de una manera que mapee la reflexión de frecuencia más baja de cero a cero y los polos restantes según sea necesario para mantener la banda de paso de equi-rizado. El cero de reflexión de frecuencia más baja se puede encontrar en los nodos de Chebyshev . La función completa de mapeo de polos de Chebyshev se muestra a continuación. ^[5] ${\displaystyle cos{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}$

${\displaystyle P'=\left[{\sqrt {\left({\frac {P^{2}+cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}{1-{cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}}}\right)}}\right]_{\text{Left Half Plane }}}$

Dónde:

n es el orden del filtro (debe ser par)

P es un polo de función de transferencia tradicional de Chebyshev

P' es el polo mapeado para la función de transferencia de orden par modificada.

"Medio plano izquierdo" indica que se utiliza la raíz cuadrada que contiene un valor real negativo.

Cuando se completa, se crea una función de transferencia de ondulación equivalente de reemplazo con valores de matriz de dispersión de reflexión cero para S12 de uno y S11 de cero cuando se implementa con redes pasivas igualmente terminadas.

Las fórmulas de valor del elemento LC en la topología de Cauer no son aplicables a la función de transferencia de Chebyshev modificada en orden par y no se pueden utilizar. Por lo tanto, es necesario calcular los valores LC a partir de fracciones continuas tradicionales de la función de impedancia, que pueden derivarse del coeficiente de reflexión , que a su vez puede derivarse de la función de transferencia.

Configuración de la atenuación de corte

La atenuación de corte de la banda de paso para los filtros Chebyshev suele ser la misma que la atenuación de ondulación de la banda de paso, establecida mediante el cálculo anterior. Sin embargo, muchas aplicaciones, como diplexores y triplexores, requieren una atenuación de corte de -3,0103 dB para obtener las reflexiones necesarias. Otras aplicaciones especializadas pueden requerir otros valores específicos para la atenuación de corte por diversos motivos. Por lo tanto, es útil tener un medio disponible para configurar la atenuación de corte de la banda de paso de Chebyshev independientemente de la atenuación de ondulación de la banda de paso, tal como -1 dB, -10 dB, etc. La atenuación de corte se puede configurar escalando la frecuencia de los polos de la función de transferencia.

El factor de escala se puede determinar mediante manipulación algebraica directa de la función de filtro de Chebyshev definitoria, incluyendo y . Se requiere la definición general de la función de Chebyshev , que puede derivarse de las ecuaciones de los polinomios de Chebyshev y de la función de Chebyshev inversa . Para mantener los números reales para los valores de , se pueden usar identidades hiperbólicas complejas para reescribir las ecuaciones como, y . ${\displaystyle G_{n}(\omega )}$ ${\displaystyle \varepsilon }$ ${\displaystyle T_{n}(\omega /\omega _{0})}$ ${\displaystyle T_{n}(\omega /\omega _{0})=cos(n\cos ^{-1}(\omega /\omega _{0}))}$ ${\displaystyle T_{n}^{-1}(\omega /\omega _{0})=cos(\cos ^{-1}(\omega /\omega _{0})/n)}$ ${\displaystyle \omega /\omega _{0}\geq 1}$ ${\displaystyle T_{n}(\omega /\omega _{0})=cosh(n\cosh ^{-1}(\omega /\omega _{0}))}$ ${\displaystyle T_{n}^{-1}(\omega /\omega _{0})=cosh(\cosh ^{-1}(\omega /\omega _{0})/n)}$

Usando álgebra simple sobre las ecuaciones y referencias anteriores, la expresión para escalar cada polo de Chebyshev es:

${\displaystyle {\begin{aligned}p_{A}&=p_{1}/T_{n}^{-1}{\Biggr (}{\sqrt {\frac {10^{{-\alpha }/10}-1}{10^{-\delta /10}-1}}},n{\Biggr )}\qquad &{\text{For }}0\geq \delta \geq -\infty {\text{ and }}0\geq \alpha >-\infty \\&=p_{1}*sech{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{-\alpha /10}-1}{10^{-\delta /10}-1}}}{\Bigr )}{\Biggr )}&{\text{For }}0\geq \delta \geq -\infty {\text{ and }}\delta \geq \alpha >-\infty \\\end{aligned}}}$

Dónde:

${\displaystyle p_{A}}$¿Está el polo reubicado posicionado para establecer la atenuación de corte deseada?

${\displaystyle p_{1}}$es un poste de corte ondulado que se encuentra en el óvalo.

${\displaystyle \delta }$es la ondulación de atenuación de la banda de paso en dB (-0,05 dB, -1 dB, etc.)).

${\displaystyle \alpha }$es la atenuación de banda de paso deseada en la frecuencia de corte en dB (−1 dB, -3 dB, −10 dB, etc.)

${\displaystyle n}$es el número de polos (el orden del filtro).

Una rápida comprobación de la cordura de la ecuación anterior utilizando la atenuación de ondulación de la banda de paso para la atenuación de corte de la banda de paso revela que el ajuste del polo será 1,0 para este caso, que es lo que se espera. ${\displaystyle (\alpha =\delta )}$

Ajuste de atenuación de corte modificado de orden uniforme

Para los filtros Chebyshev que se diseñan con ondulación de banda de paso de orden par modificado para filtros pasivos con terminaciones iguales, el cálculo de la frecuencia de atenuación debe incluir el ajuste de orden par realizando la operación de ajuste de orden par en la frecuencia de atenuación calculada. Esto hace que la aritmética de ajuste de orden par sea un poco más simple, ya que la frecuencia se puede tratar como una variable real, en este caso . ${\displaystyle ((J\omega )^{2}{\text{ becomes }}-\omega ^{2})}$

${\displaystyle {\begin{aligned}p_{A}=p_{1}{\sqrt {\frac {1-{cos^{2}({\frac {\pi (n-1)}{2n}})}}{cosh^{2}{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{-\alpha /10}-1}{10^{-\delta /10}-1}}}{\Bigr )}{\Biggr )}-cos^{2}({\frac {\pi (n-1)}{2n}})}}}{\text{ For }}0\geq \delta \geq -\infty {\text{ and }}\delta \geq \alpha >-\infty \\\end{aligned}}}$

Dónde:

${\displaystyle p_{A}}$¿Está el polo reubicado posicionado para establecer la atenuación de corte deseada?

${\displaystyle p_{1}}$es un poste de corte ondulado que ha sido modificado para bandas de paso de orden uniforme.

${\displaystyle \delta }$es la ondulación de atenuación de la banda de paso en dB (-0,05 dB, -1 dB, etc.)).

${\displaystyle \alpha }$es la atenuación de banda de paso deseada en la frecuencia de corte en dB (−1 dB, -3 dB, −10 dB, etc.)

${\displaystyle n}$es el número de polos (el orden del filtro).

${\displaystyle cos({\frac {\pi (n-1)}{2n}})}$es el nodo de Chebyshev de orden par más pequeño

Filtros Chebyshev tipo II (filtros Chebyshev inversos)

La respuesta de frecuencia de un filtro de paso bajo Chebyshev tipo II de quinto orden con ${\displaystyle \varepsilon =0.01}$

También conocido como filtro Chebyshev inverso, el tipo de filtro Chebyshev Tipo II es menos común porque no se desliza tan rápido como el Tipo I y requiere más componentes. No tiene ondulación en la banda de paso, pero sí tiene ondulación en la banda de parada. La ganancia es:

${\displaystyle G_{n}(\omega )={\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}}}}}={\sqrt {\frac {\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}{1+\varepsilon ^{2}T_{n}^{2}(\omega _{0}/\omega )}}}.}$

En la banda de parada, el polinomio de Chebyshev oscila entre -1 y 1, por lo que la ganancia oscilará entre cero y

${\displaystyle {\frac {1}{\sqrt {1+{\frac {1}{\varepsilon ^{2}}}}}}}$

y la frecuencia más pequeña a la que se alcanza este máximo es la frecuencia de corte . Por tanto, el parámetro ε está relacionado con la atenuación de la banda de parada γ en decibelios mediante: ${\displaystyle \omega _{o}}$

${\displaystyle \varepsilon ={\frac {1}{\sqrt {10^{\gamma /10}-1}}}.}$

Para una atenuación de banda suprimida de 5 dB, ε = 0,6801; para una atenuación de 10 dB, ε = 0,3333. La frecuencia f ₀ = ω ₀ /2 π es la frecuencia de corte. La frecuencia de 3 dB f _H está relacionada con f ₀ por:

${\displaystyle f_{H}={\frac {f_{0}}{\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right)}}.}$

Polos y ceros

Registro del valor absoluto de la ganancia de un filtro Chebyshev tipo II de octavo orden en un espacio de frecuencia complejo (s=σ+jω) con ε = 0,1 y . Los puntos blancos son polos y los puntos negros son ceros. Se muestran los 16 polos. Cada cero tiene multiplicidad de dos, y se muestran 12 ceros y cuatro están ubicados fuera de la imagen, dos en el eje ω positivo y dos en el negativo. Los polos de la función de transferencia son polos en el semiplano izquierdo y los ceros de la función de transferencia son los ceros, pero con multiplicidad 1. El negro corresponde a una ganancia de 0,05 o menos, el blanco corresponde a una ganancia de 20 o más. ${\displaystyle \omega _{0}=1}$

Suponiendo que la frecuencia de corte es igual a la unidad, los polos de la ganancia del filtro Chebyshev son los ceros del denominador de la ganancia: ${\displaystyle (\omega _{pm})}$

${\displaystyle 1+\varepsilon ^{2}T_{n}^{2}(-1/js_{pm})=0.}$

Los polos de ganancia del filtro Chebyshev tipo II son inversos a los polos del filtro tipo I:

${\displaystyle {\frac {1}{s_{pm}^{\pm }}}=\pm \sinh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\sin(\theta _{m})}$

${\displaystyle \qquad +j\cosh \left({\frac {1}{n}}\mathrm {arsinh} \left({\frac {1}{\varepsilon }}\right)\right)\cos(\theta _{m})}$

dónde . Los ceros del filtro Chebyshev tipo II son los ceros del numerador de la ganancia: ${\displaystyle m=1,2,...n}$ ${\displaystyle (\omega _{zm})}$

${\displaystyle \varepsilon ^{2}T_{n}^{2}(-1/js_{zm})=0.\,}$

Los ceros del filtro de Chebyshev tipo II son, por tanto, la inversa de los ceros del polinomio de Chebyshev.

${\displaystyle 1/s_{zm}=-j\cos \left({\frac {\pi }{2}}\,{\frac {2m-1}{n}}\right)}$

para . ${\displaystyle m=1,2,...n}$

La función de transferencia

La función de transferencia está dada por los polos en el semiplano izquierdo de la función de ganancia y tiene los mismos ceros, pero estos ceros son ceros simples en lugar de dobles.

El retraso del grupo

Ganancia y retardo de grupo de un filtro Chebyshev tipo II de quinto orden con ε = 0,1.

La ganancia y el retardo de grupo para un filtro Chebyshev tipo II de quinto orden con ε = 0,1 se representan en el gráfico de la izquierda. Se puede observar que hay ondulaciones en la ganancia en la banda de parada pero no en la banda de paso.

Implementación

topología de cauer

Se puede realizar un filtro de paso bajo LC Chebyshev pasivo utilizando una topología de Cauer . Los valores del inductor o condensador de un filtro prototipo Chebyshev de orden th se pueden calcular a partir de las siguientes ecuaciones: ^[6] ${\displaystyle n}$

${\displaystyle G_{0}=1}$

${\displaystyle G_{1}={\frac {2A_{1}}{\gamma }}}$

${\displaystyle G_{k}={\frac {4A_{k-1}A_{k}}{B_{k-1}G_{k-1}}},\qquad k=2,3,4,\dots ,n}$

${\displaystyle G_{n+1}={\begin{cases}1&{\text{if }}n{\text{ odd}}\\\coth ^{2}\left({\frac {\beta }{4}}\right)&{\text{if }}n{\text{ even}}\end{cases}}}$

G ₁ , G _k son los valores del elemento condensador o inductor. f _H , la frecuencia de 3 dB se calcula con: ${\displaystyle f_{H}=f_{0}\cosh \left({\frac {1}{n}}\cosh ^{-1}{\frac {1}{\varepsilon }}\right)}$

Los coeficientes A , γ , β , A _k y B _k se pueden calcular a partir de las siguientes ecuaciones:

${\displaystyle \gamma =\sinh \left({\frac {\beta }{2n}}\right)}$

${\displaystyle \beta =\ln \left[\coth \left({\frac {\delta }{17.37}}\right)\right]}$

${\displaystyle A_{k}=\sin {\frac {(2k-1)\pi }{2n}},\qquad k=1,2,3,\dots ,n}$

${\displaystyle B_{k}=\gamma ^{2}+\sin ^{2}\left({\frac {k\pi }{n}}\right),\qquad k=1,2,3,\dots ,n}$

¿ Dónde está la ondulación de la banda de paso en decibeles? El número se redondea desde el valor exacto . ${\displaystyle \delta }$ ${\displaystyle 17.37}$ ${\displaystyle 40/\ln(10)}$

Filtro de paso bajo usando topología Cauer

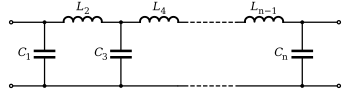
Los valores de Gk calculados _pueden luego convertirse en capacitores en derivación e inductores en serie como se muestra a la derecha, o pueden convertirse en capacitores en serie e inductores en derivación. Por ejemplo,

• _Derivación C 1 = G ₁ , serie L ₂ = G ₂ , ...

o

• L _{1 derivación} = G ₁ , C _{1 serie} = G ₂ , ...

Tenga en cuenta que cuando G ₁ es un condensador en derivación o un inductor en serie, G ₀ corresponde a la resistencia o conductancia de entrada, respectivamente. La misma relación se cumple para G _n+1 y G _n . El circuito resultante es un filtro de paso bajo normalizado. Utilizando transformaciones de frecuencia y escalado de impedancia , el filtro de paso bajo normalizado se puede transformar en filtros de paso alto , paso de banda y supresión de banda de cualquier frecuencia de corte o ancho de banda deseado .

Digital

Como ocurre con la mayoría de los filtros analógicos, el Chebyshev se puede convertir a una forma recursiva digital (en tiempo discreto) mediante la transformada bilineal . Sin embargo, como los filtros digitales tienen un ancho de banda finito, la forma de respuesta del Chebyshev transformado está deformada . Alternativamente, se puede utilizar el método de transformación Z coincidente , que no deforma la respuesta.

Comparación con otros filtros lineales

La siguiente ilustración muestra los filtros de Chebyshev junto a otros tipos de filtros comunes obtenidos con el mismo número de coeficientes (quinto orden):

Los filtros Chebyshev son más nítidos que el filtro Butterworth ; No son tan nítidos como el elíptico , pero muestran menos ondulaciones en el ancho de banda.

Ver también

• filtro de bessel
• filtro de mantequilla
• Nodos de Chebyshev
• polinomio de Chebyshev
• Filtro de peine
• Filtro elíptico
• Diseño de filtro

Referencias

1. Daniels, Richard W. (1974). Métodos de aproximación para el diseño de filtros electrónicos . Nueva York: McGraw-Hill. ISBN 0-07-015308-6.
2. Lutovac, Miroslav D.; Lutovac, D.; Tošić, Dejan V.; Evans, Brian Lawrence (2001). Diseño de filtros para procesamiento de señales utilizando MATLAB y Mathematica. Prentice Hall. ISBN 9780201361308.
3. Weinberg, Luis; Slepian, Paul (junio de 1960). "Resultados de Takahasi en Tchebycheff y Butterworth Ladder Networks". Transacciones IRE sobre teoría de circuitos . 7 (2): 88-101. doi :10.1109/TCT.1960.1086643.
4. Williams, Arthur B.; Taylors, Fred J. (1988). Manual de diseño de filtros electrónicos . Nueva York: McGraw-Hill. ISBN 0-07-070434-1.
5. Saal, Rudolf (enero de 1979). Manual de diseño de filtros (en inglés y alemán) (1ª ed.). Múnich, Alemania: Allgemeine Elektricitais-Gesellschaft. págs. 56–61. ISBN 3-87087-070-2.
6. Matthaei, George L.; Joven, Leo; Jones, paramédico (1980). Filtros de microondas, redes de adaptación de impedancia y estructuras de acoplamiento . Norwood, MA: Casa Artech. ISBN 0-89-006099-1.

enlaces externos

• Medios relacionados con los filtros de Chebyshev en Wikimedia Commons