Onda de giro

En física de la materia condensada , una onda de espín es una perturbación que se propaga en el ordenamiento de un material magnético . Estas excitaciones colectivas de baja altitud se producen en redes magnéticas con simetría continua . Desde el punto de vista de las cuasipartículas equivalentes , las ondas de espín se conocen como magnones , que son modos bosónicos de la red de espín que corresponden aproximadamente a las excitaciones de fonones de la red nuclear. A medida que aumenta la temperatura, la excitación térmica de las ondas de espín reduce la magnetización espontánea de un ferroimán . Las energías de las ondas de espín son típicamente de solo $μeV$ de acuerdo con los puntos de Curie típicos a temperatura ambiente y por debajo.

Teoría

Una ilustración de la precesión de una onda de espín con una longitud de onda que es once veces la constante reticular alrededor de un campo magnético aplicado.

La proyección de la magnetización de la misma onda de espín a lo largo de la dirección de la cadena en función de la distancia a lo largo de la cadena de espín.

La forma más sencilla de comprender las ondas de espín es considerar el hamiltoniano para el ferroimán de Heisenberg : ${\mathcal {H}}$

{\mathcal {H}}=-{\frac {1}{2}}J\sum _{i,j}\mathbf {S} _{i}\cdot \mathbf {S} _{j }-g\mu _{\rm {B}}\sum _{i}\mathbf {H} \cdot \mathbf {S} _{i}

donde $J$ es la energía de intercambio , los operadores $S$ representan los espines en los puntos de la red de Bravais , $g$ es el factor g de Landé , $μB$ es el magnetón de Bohr y $H$ es el campo interno que incluye el campo externo más cualquier campo "molecular". Nótese que en el caso del continuo clásico y en dimensiones $1 + 1$ $la$ ecuación del ferroimán de Heisenberg tiene la forma

\mathbf {S} _{t}=\mathbf {S} \times \mathbf {S} _{xx}.

En las dimensiones $1+1, 2+1$ y $3+1$ esta ecuación admite varias extensiones integrables y no integrables como la ecuación de Landau-Lifshitz , la ecuación de Ishimori , etc. Para un ferroimán $J > 0$ y el estado fundamental del hamiltoniano es aquel en el que todos los espines están alineados en paralelo con el campo $H.$ Esto es un estado propio de que se puede verificar reescribiéndolo en términos de los operadores de elevación y reducción de espín dados por: $|0\rangle$ $|0\rangle$ ${\mathcal {H}}$

S^{\pm}=S^{x}\pm iS^{y}

Resultando en

{\mathcal {H}}=-{\frac {1}{2}}J\sum _{i,j}S_{i}^{z}S_{j}^{z}-g\mu _{\rm {B}}H\sum _{i}S_{i}^{z}-{\frac {1}{4}}J\sum _{i,j}(S_{i}^{+}S_{j}^{-}+S_{i}^{-}S_{j}^{+})

donde $z$ se ha tomado como la dirección del campo magnético. El operador de reducción de espín $S -$ aniquila el estado con mínima proyección de espín a lo largo del eje $z$ , mientras que el operador de aumento de espín $S +$ aniquila el estado fundamental con máxima proyección de espín a lo largo del eje $z$ .

S_{i}^{z}|0\rangle =s|0\rangle

Para el estado de alineación máxima, encontramos

{\mathcal {H}}|0\rangle =\left(-Js^{2}-g\mu _{\rm {B}}Hs\right)N|0\rangle

donde N es el número total de sitios de la red de Bravais. Se confirma la proposición de que el estado fundamental es un estado propio del hamiltoniano.

Se podría suponer que el primer estado excitado del hamiltoniano tiene un giro seleccionado aleatoriamente en la posición $i$ rotado de manera que

S_{i}^{z}|1\rangle =(s-1)|1\rangle,

pero de hecho esta disposición de espines no es un estado propio. La razón es que tal estado es transformado por los operadores de elevación y reducción de espín. El operador aumentará la proyección $z$ del espín en la posición $i$ de nuevo a su orientación de baja energía, pero el operador reducirá la proyección $z$ del espín en la posición $j$ . El efecto combinado de los dos operadores es, por tanto, propagar el espín rotado a una nueva posición, lo que es un indicio de que el estado propio correcto es una onda de espín , es decir, una superposición de estados con un espín reducido. La penalización de energía de intercambio asociada con el cambio de orientación de un espín se reduce al extender la perturbación sobre una longitud de onda larga. De este modo se minimiza el grado de desorientación de dos espines vecinos cualesquiera. A partir de esta explicación se puede ver por qué el imán del modelo de Ising con simetría discreta no tiene ondas de espín: la noción de extender una perturbación en la red de espín sobre una longitud de onda larga no tiene sentido cuando los espines solo tienen dos orientaciones posibles. La existencia de excitaciones de baja energía está relacionada con el hecho de que, en ausencia de un campo externo, el sistema de espín tiene un número infinito de estados fundamentales degenerados con orientaciones de espín infinitesimalmente diferentes. La existencia de estos estados fundamentales se puede ver a partir del hecho de que el estado no tiene la simetría rotacional completa del hamiltoniano , un fenómeno que se denomina ruptura espontánea de la simetría . $Estilo de visualización S_{i}^{+}}$ $Estilo de visualización S_ {j}^{-}}$ $|0\rangle$ ${\mathcal {H}}$

Magnetización

En este modelo la magnetización

M={\frac {N\mu _{\rm {B}}gs}{V}}

donde $V$ es el volumen. La propagación de las ondas de espín se describe mediante la ecuación de movimiento de Landau-Lifshitz:

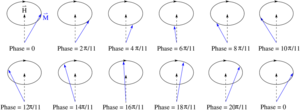
{\frac {d\mathbf {M} }{dt}}=-\gamma \mathbf {M} \times \mathbf {H} -{\frac {\lambda \mathbf {M} \times (\ matemáticasbf {M} \times \mathbf {H} )}{M^{2}}}

donde $γ$ es la relación giromagnética y $λ$ es la constante de amortiguamiento. Los productos cruzados en esta ecuación de aspecto amenazante muestran que la propagación de las ondas de espín está gobernada por los pares generados por los campos internos y externos. (Una forma equivalente es la ecuación de Landau-Lifshitz-Gilbert , que reemplaza el término final por uno equivalente de aspecto más "simple").

El primer término del lado derecho de la ecuación describe la precesión de la magnetización bajo la influencia del campo aplicado, mientras que el término final mencionado anteriormente describe cómo el vector de magnetización "se mueve en espiral" hacia la dirección del campo a medida que avanza el tiempo. En los metales, las fuerzas de amortiguación descritas por la constante $λ$ están dominadas en muchos casos por las corrientes de Foucault.

Una diferencia importante entre fonones y magnones radica en sus relaciones de dispersión . La relación de dispersión para fonones es lineal de primer orden en el vector de onda $k$ , es decir, $ώ = ck$ , donde $ω$ es la frecuencia y $c$ es la velocidad del sonido. Los magnones tienen una relación de dispersión parabólica: $ώ = Ak 2$ donde el parámetro $A$ representa una " rigidez de espín ". La forma $k 2$ es el tercer término de una expansión de Taylor de un término coseno en la expresión de energía que se origina a partir del producto escalar $S i \cdot S j$ . La razón subyacente para la diferencia en la relación de dispersión es que el parámetro de orden (magnetización) para el estado fundamental en los ferroimanes viola la simetría de inversión temporal . Dos espines adyacentes en un sólido con constante reticular $a$ que participan en un modo con vector de onda $k$ tienen un ángulo entre ellos igual a $ka$ .

Observación experimental

Las ondas de espín se observan a través de cuatro métodos experimentales: dispersión inelástica de neutrones , dispersión inelástica de luz ( dispersión de Brillouin , dispersión Raman y dispersión inelástica de rayos X ), dispersión inelástica de electrones ( espectroscopia de pérdida de energía de electrones resuelta en espín ) y resonancia de ondas de espín ( resonancia ferromagnética ).

En la dispersión inelástica de neutrones se mide la pérdida de energía de un haz de neutrones que excita un magnón, normalmente en función del vector de dispersión (o equivalentemente, la transferencia de momento), la temperatura y el campo magnético externo. Las mediciones de dispersión inelástica de neutrones pueden determinar la curva de dispersión de los magnones, al igual que de los fonones . Existen importantes instalaciones de dispersión inelástica de neutrones en la fuente de neutrones ISIS en Oxfordshire, Reino Unido, el Instituto Laue-Langevin en Grenoble , Francia, el reactor de isótopos de alto flujo en el Laboratorio Nacional Oak Ridge en Tennessee, EE. UU., y en el Instituto Nacional de Estándares y Tecnología en Maryland, EE. UU.
La dispersión de Brillouin mide de manera similar la pérdida de energía de los fotones (generalmente en una longitud de onda visible conveniente) reflejados o transmitidos a través de un material magnético. La espectroscopia de Brillouin es similar a la dispersión Raman más conocida , pero sondea una energía menor y tiene una resolución energética superior para poder detectar la energía meV de los magnones.
La resonancia ferromagnética (o antiferromagnética) mide, en cambio, la absorción de microondas , incidentes sobre un material magnético, por ondas de espín, típicamente en función del ángulo, la temperatura y el campo aplicado. La resonancia ferromagnética es un método de laboratorio conveniente para determinar el efecto de la anisotropía magnetocristalina en la dispersión de ondas de espín. Un grupo del Instituto Max Planck de Física de Microestructuras en Halle, Alemania, demostró que al utilizar espectroscopia de pérdida de energía de electrones polarizados por espín (SPEELS), se pueden excitar magnones de superficie de energía muy alta. Esta técnica permite investigar la dispersión de magnones en películas ferromagnéticas ultradelgadas. El primer experimento se realizó para una película de Fe de 5 ML. ^[1] Con resolución de momento, se exploró la dispersión de magnones para una película de Co fcc de 8 ML sobre Cu(001) y una película de Co hcp de 8 ML sobre W(110), respectivamente. ^[2] La energía máxima del magnón en el borde de la zona de Brillouin de la superficie fue de 240 meV.

Importancia práctica

Cuando los dispositivos magnetoelectrónicos funcionan a altas frecuencias, la generación de ondas de espín puede ser un mecanismo importante de pérdida de energía. La generación de ondas de espín limita los anchos de línea y, por lo tanto, los factores de calidad Q de los componentes de ferrita utilizados en dispositivos de microondas . El recíproco de la frecuencia más baja de las ondas de espín características de un material magnético proporciona una escala de tiempo para la conmutación de un dispositivo basado en ese material.

Véase también

Referencias

^ Plihal, M.; Mills, DL; Kirschner, J. (1999). "Firma de onda de espín en el espectro de pérdida de energía de electrones polarizados por espín en una película ultradelgada de Fe: teoría y experimento". Phys. Rev. Lett . 82 (12): 2579–2582. Código Bibliográfico :1999PhRvL..82.2579P. doi :10.1103/PhysRevLett.82.2579.
^ Vollmer, R.; Etzkorn, M.; Kumar, PS Anil; Ibach, H.; Kirschner, J. (29 de septiembre de 2003). "Espectroscopia de pérdida de energía de electrones polarizada por espín de ondas de espín de vector de onda grande y alta energía en películas de Co ultradelgadas de fcc sobre Cu(001)" (PDF) . Physical Review Letters . 91 (14): 147201. Bibcode :2003PhRvL..91n7201V. doi :10.1103/PhysRevLett.91.147201. PMID 14611549.

Anderson, Philip W. (1997). Conceptos de sólidos: lecciones sobre la teoría de los sólidos (edición revisada). Singapur: World Scientific. ISBN 981-02-3231-4.
Anderson, Philip W. (1997). Nociones básicas de física de la materia condensada . Cambridge, Mass.: Perseus Publishing. ISBN 0-201-32830-5.
Ashcroft, Neil W.; Mermin, N. David (1977). Física del estado sólido (27.ª ed. repr.). Nueva York: Holt, Rinehart y Winston. ISBN 0-03-083993-9.
Chikazumi, Sōshin (1997). Física del ferromagnetismo (2.ª ed.). Oxford: Oxford University Press. ISBN 0191569852.

Enlaces externos

Ondas de espín - Las conferencias Feynman sobre física
Lista de laboratorios que realizan mediciones de dispersión de Brillouin.