

En geometría , las esferas de Dandelin son una o dos esferas que son tangentes tanto a un plano como a un cono que corta al plano. La intersección del cono y el plano es una sección cónica , y el punto en el que cualquiera de las esferas toca el plano es un foco de la sección cónica, por lo que a las esferas Dandelin también se les llama a veces esferas focales . [1]
Las esferas de Dandelin fueron descubiertas en 1822. [1] [2] Reciben su nombre en honor al matemático francés Germinal Pierre Dandelin , aunque a veces también se le da crédito parcial a Adolphe Quetelet . [3] [4] [5]
Las esferas de Dandelin se pueden utilizar para dar elegantes demostraciones modernas de dos teoremas clásicos conocidos por Apolonio de Perga . El primer teorema es que una sección cónica cerrada (es decir, una elipse ) es el lugar geométrico de puntos tales que la suma de las distancias a dos puntos fijos (los focos) es constante. El segundo teorema es que para cualquier sección cónica, la distancia desde un punto fijo (el foco) es proporcional a la distancia desde una línea fija (la directriz ), llamándose excentricidad a la constante de proporcionalidad . [6]
Una sección cónica tiene una esfera Dandelin para cada foco. Una elipse tiene dos esferas de Dandelin que tocan la misma nuca del cono, mientras que la hipérbola tiene dos esferas de Dandelin que tocan napas opuestas. Una parábola tiene solo una esfera de diente de león.
Considere la ilustración que representa un cono con el vértice S en la parte superior. Un plano e corta al cono en una curva C (con interior azul). La siguiente prueba demostrará que la curva C es una elipse.
Las dos esferas marrones de Dandelin, G 1 y G 2 , se colocan tangentes tanto al plano como al cono: G 1 encima del plano, G 2 debajo. Cada esfera toca el cono a lo largo de un círculo (de color blanco) y .
Denotemos el punto de tangencia del avión con G 1 por F 1 , y de manera similar para G 2 y F 2 . Sea P un punto típico de la curva C.
Para demostrar: La suma de distancias permanece constante mientras el punto P se mueve a lo largo de la curva de intersección C. (Ésta es una definición de que C es una elipse, con y siendo sus focos).
Esto da una prueba diferente de un teorema de Apolonio de Perga . [6]
Si definimos una elipse como el lugar geométrico de los puntos P tales que d ( F 1 , P ) + d ( F 2 , P ) = una constante, entonces el argumento anterior demuestra que la curva de intersección C es de hecho una elipse. Que la intersección del plano con el cono sea simétrica con respecto a la bisectriz perpendicular de la recta que pasa por F 1 y F 2 puede ser contrario a la intuición, pero este argumento lo deja claro.
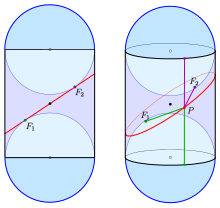
Las adaptaciones de este argumento funcionan para hipérbolas y parábolas como intersecciones de un plano con un cono. Otra adaptación funciona para una elipse realizada como la intersección de un plano con un cilindro circular recto .
La directriz de una sección cónica se puede encontrar utilizando la construcción de Dandelin. Cada esfera de Dandelin cruza el cono en un círculo; Dejemos que ambos círculos definan sus propios planos. Las intersecciones de estos dos planos paralelos con el plano de la sección cónica serán dos rectas paralelas; estas líneas son las directrices de la sección cónica. Sin embargo, una parábola tiene sólo una esfera de Dandelin y, por tanto, tiene una sola directriz.
Utilizando las esferas de Dandelin, se puede demostrar que cualquier sección cónica es el lugar geométrico de los puntos para los cuales la distancia desde un punto (foco) es proporcional a la distancia desde la directriz. [7] Los antiguos matemáticos griegos como Pappus de Alejandría eran conscientes de esta propiedad, pero las esferas de Dandelin facilitan la prueba. [6]
Ni Dandelin ni Quetelet utilizaron las esferas de Dandelin para demostrar la propiedad foco-directriz. El primero en hacerlo pudo haber sido Pierce Morton en 1829, [8] o quizás Hugh Hamilton , quien observó (en 1758) que una esfera toca el cono en un círculo que define un plano cuya intersección con el plano de la sección cónica es un directora. [1] [9] [10] [11] La propiedad foco-directriz se puede utilizar para demostrar que los objetos astronómicos se mueven a lo largo de secciones cónicas alrededor del Sol. [12]