

La escala de 833 cents es una afinación y escala musical propuesta por Heinz Bohlen [ aclaración necesaria ] basada en tonos de combinación , un intervalo de 833,09 cents y, coincidentemente, la secuencia de Fibonacci . [1] La proporción áurea es , que como intervalo musical es 833,09 cents ( ). En la escala de 833 cents este intervalo se toma como una alternativa a la octava como intervalo de repetición , [2] sin embargo la proporción áurea no se considera un intervalo equivalente (las notas separadas 833,09 cents no son "lo mismo" en la escala de 833 cents de la misma manera que las notas separadas 1200 cents en las afinaciones tradicionales). Otros teóricos musicales como Walter O'Connell, en su obra "La tonalidad de la sección áurea" de 1993, [3] y Lorne Temes en 1970, [4] parecen haber creado también esta escala antes de que Bohlen la descubriera.

Partiendo de cualquier intervalo, se toma el intervalo producido por el tono original más alto y el tono de combinación más cercano. Luego se hace lo mismo para ese intervalo. Estos intervalos " convergen a un valor cercano a 833 centésimas. Eso no significa nada más que, por ejemplo, para un intervalo de 144:89 (833,11 centésimas), tanto el tono de suma como el de diferencia aparecen... de nuevo a 833 centésimas de distancia de este intervalo". [1]
Por ejemplo, 220 Hz y 220 Hz (unísono) producen tonos combinados a 0 y 440 Hz. 440 Hz es una octava por encima de 220 Hz. 220 Hz y 440 Hz producen tonos combinados a 220 Hz y 660 Hz. 660 Hz es una quinta perfecta (3:2) por encima de 440 Hz, y produce tonos combinados a 220 Hz y 1.100 Hz. 1.100 Hz es una sexta mayor (5:3) por encima de 660 Hz, y produce tonos combinados a 440 Hz y 1.760 Hz. 1100 Hz y 1760 Hz son una sexta menor (8:5), y así sucesivamente. "Por cierto, no es importante qué intervalo elijamos como punto de partida para el ejercicio anterior; el resultado es siempre 833 cent." [1]
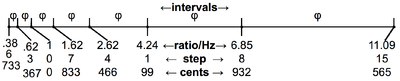
Una vez determinado el intervalo de 833,09 céntimos se produce una pila de ellos:
También se producen dos pilas en 3:2 y su inverso 4:3 para proporcionar los pasos 2 y 5, creando una red bidimensional . Dado que la proporción áurea es un número irracional, hay tres pilas infinitas de posibles proporciones áureas que nunca vuelven exactamente al unísono o a la octava. El paso de escala 5 es 597,32 centésimas y el paso de escala -5 es 602,68 centésimas (con una diferencia de 5,37 centésimas).
Bohlen describe una escala simétrica de siete tonos , en la que los tonos de los pasos 0, 1, 3, 4 y 6 se derivan de la pila de intervalos de proporción áurea.

Esto es comparable a la derivación de la escala mayor a partir de una pila de quintas perfectas (FCGDAEB = CDEFGAB). Véase: Colección generada .
La escala "contiene una red de relaciones armónicas con la propiedad de coincidir con ciclos de intervalos armónicos de 833 centésimas". [5] Los pasos 2 y 5 fueron presumiblemente elegidos para llenar los espacios entre lo que se convertirían en los pasos 1 y 3 y 4 y 6 (267,64 centésimas). El valor del paso 2 (235,77) fue elegido para crear una doceava perfecta (quinta perfecta compuesta) entre los pasos 16 (235,77+833,09+833,09) y el paso 0, y una vez elegido determinó el valor del paso 5 debido a la simetría de la escala. Los pasos 10 y 0 forman una octava. Todas las notas separadas por 7 pasos forman la proporción áurea entre sí, por ejemplo 16 y 9 y 10 y 3.
Se puede observar la repetición de frecuencias y la coincidencia de pasos más altos con consonancias como la quinta y la octava perfectas (el número de paso de los intervalos que coinciden con la pila de proporciones áureas está en negrita, mientras que las proporciones de los intervalos repetidos están en negrita):
La escala contiene 0,83333 × 12 pasos por octava (≈10). [5] Si bien lo ideal es que no esté temperada, la escala puede aproximarse mediante el temperamento igual 36 , una ventaja es que el temperamento igual 36 incluye el temperamento tradicional 12-TET. [2]