El error de observación (o error de medición ) es la diferencia entre un valor medido de una cantidad y su valor verdadero desconocido . [1] Estos errores son inherentes al proceso de medición; por ejemplo, las longitudes medidas con una regla calibrada en centímetros enteros tendrán un error de medición de varios milímetros. El error o incertidumbre de una medición se puede estimar y se especifica con la medición como, por ejemplo, 32,3 ± 0,5 cm. (Un error o equivocación en el proceso de medición dará un valor incorrecto , en lugar de uno sujeto a un error de medición conocido).
Los errores de medición se pueden dividir en dos componentes: aleatorios y sistemáticos . [2] Los errores aleatorios son errores en la medición que llevan a que los valores mensurables sean inconsistentes cuando se toman mediciones repetidas de un atributo o cantidad constante . Los errores sistemáticos son errores que no están determinados por el azar sino que son introducidos por procesos repetibles inherentes al sistema . [3] El error sistemático también puede referirse a un error con una media distinta de cero , cuyo efecto no se reduce cuando se promedian las observaciones . [ cita requerida ] Por ejemplo, las mediciones de longitud con una regla calibrada con precisión en centímetros enteros estarán sujetas a error aleatorio; una regla calibrada incorrectamente también producirá error sistemático.
Los errores de medición se pueden resumir en términos de exactitud y precisión . El error de medición no debe confundirse con la incertidumbre de medición .
Cuando se atribuyen a dichos errores la aleatoriedad o la incertidumbre modelada por la teoría de la probabilidad , son "errores" en el sentido en que se utiliza ese término en estadística ; véase errores y residuos en estadística .
Cada vez que se repite una medición se obtienen resultados ligeramente diferentes. El modelo estadístico común que se utiliza es que el error tiene dos partes aditivas:
El error sistemático se denomina a veces sesgo estadístico y suele reducirse con procedimientos estandarizados. Parte del proceso de aprendizaje en las distintas ciencias consiste en aprender a utilizar instrumentos y protocolos estandarizados para minimizar el error sistemático.
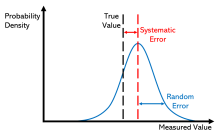
El error aleatorio (o variación aleatoria ) se debe a factores que no se pueden o no se quieren controlar. Una posible razón para no controlar estos errores aleatorios es que puede resultar demasiado costoso controlarlos cada vez que se realiza el experimento o se toman las mediciones. Otras razones pueden ser que lo que estamos tratando de medir está cambiando en el tiempo (ver modelos dinámicos ), o es fundamentalmente probabilístico (como es el caso de la mecánica cuántica; ver Medición en mecánica cuántica ). El error aleatorio a menudo ocurre cuando los instrumentos se llevan al extremo de sus límites operativos. Por ejemplo, es común que las balanzas digitales muestren un error aleatorio en su dígito menos significativo. Tres mediciones de un solo objeto podrían leer algo así como 0,9111 g, 0,9110 g y 0,9112 g.
Los errores de medición se pueden dividir en dos componentes: error aleatorio y error sistemático. [2]
Los errores aleatorios siempre están presentes en una medición. Son causados por fluctuaciones inherentemente impredecibles en las lecturas de un aparato de medición o en la interpretación que hace el experimentador de la lectura instrumental. Los errores aleatorios se manifiestan como resultados diferentes para aparentemente la misma medición repetida. Se pueden estimar comparando múltiples mediciones y reducir promediando múltiples mediciones.
El error sistemático es predecible y, por lo general, constante o proporcional al valor real. Si se puede identificar la causa del error sistemático, generalmente se puede eliminar. Los errores sistemáticos son causados por una calibración imperfecta de los instrumentos de medición o métodos de observación imperfectos , o por la interferencia del entorno con el proceso de medición, y siempre afectan los resultados de un experimento en una dirección predecible. La puesta a cero incorrecta de un instrumento es un ejemplo de error sistemático en la instrumentación.
La norma de pruebas de rendimiento PTC 19.1-2005 "Incertidumbre de las pruebas", publicada por la Sociedad Estadounidense de Ingenieros Mecánicos (ASME), analiza los errores sistemáticos y aleatorios con gran detalle. De hecho, conceptualiza sus categorías básicas de incertidumbre en esos términos.
El error aleatorio puede ser causado por fluctuaciones impredecibles en las lecturas de un aparato de medición o en la interpretación que hace el experimentador de la lectura instrumental; estas fluctuaciones pueden deberse en parte a la interferencia del entorno con el proceso de medición. El concepto de error aleatorio está estrechamente relacionado con el concepto de precisión . Cuanto mayor sea la precisión de un instrumento de medición, menor será la variabilidad ( desviación estándar ) de las fluctuaciones en sus lecturas.
Las fuentes de error sistemático pueden ser la calibración imperfecta de los instrumentos de medición (error cero), los cambios en el entorno que interfieren con el proceso de medición y, a veces, los métodos de observación imperfectos pueden ser de error cero o de error porcentual. Si consideramos a un experimentador que toma una lectura del período de tiempo de un péndulo que oscila más allá de un marcador fiducial : si su cronómetro o temporizador comienza con 1 segundo en el reloj, entonces todos sus resultados estarán desfasados por 1 segundo (error cero). Si el experimentador repite este experimento veinte veces (comenzando con 1 segundo cada vez), entonces habrá un error porcentual en el promedio calculado de sus resultados; el resultado final será ligeramente mayor que el período real.
La distancia medida por radar se sobrestimará sistemáticamente si no se tiene en cuenta la ligera desaceleración de las ondas en el aire. La puesta a cero incorrecta de un instrumento es un ejemplo de error sistemático en la instrumentación.
Los errores sistemáticos también pueden estar presentes en el resultado de una estimación basada en un modelo matemático o una ley física . Por ejemplo, la frecuencia de oscilación estimada de un péndulo será sistemáticamente errónea si no se tiene en cuenta un ligero movimiento del soporte.
Los errores sistemáticos pueden ser constantes o estar relacionados (por ejemplo, de forma proporcional o porcentual) con el valor real de la magnitud medida, o incluso con el valor de una magnitud diferente (la lectura de una regla puede verse afectada por la temperatura ambiental). Cuando es constante, se debe simplemente a una puesta a cero incorrecta del instrumento. Cuando no es constante, puede cambiar su signo. Por ejemplo, si un termómetro se ve afectado por un error sistemático proporcional igual al 2% de la temperatura real, y la temperatura real es 200°, 0° o −100°, la temperatura medida será 204° (error sistemático = +4°), 0° (error sistemático nulo) o −102° (error sistemático = −2°), respectivamente. Por lo tanto, la temperatura se sobrestimará cuando esté por encima de cero y se subestimará cuando esté por debajo de cero.
Los errores sistemáticos que cambian durante un experimento ( deriva ) son más fáciles de detectar. Las mediciones indican tendencias con el tiempo en lugar de variar aleatoriamente alrededor de una media . La deriva es evidente si una medición de una cantidad constante se repite varias veces y las mediciones se desvían en una dirección durante el experimento. Si la siguiente medición es mayor que la medición anterior, como puede ocurrir si un instrumento se calienta durante el experimento, entonces la cantidad medida es variable y es posible detectar una deriva verificando la lectura de cero durante el experimento, así como al comienzo del experimento (de hecho, la lectura de cero es una medición de una cantidad constante). Si la lectura de cero está constantemente por encima o por debajo de cero, existe un error sistemático. Si esto no se puede eliminar, posiblemente reiniciando el instrumento inmediatamente antes del experimento, entonces se debe permitir restando su valor (posiblemente variable en el tiempo) de las lecturas y tomándolo en cuenta al evaluar la precisión de la medición.
Si no se observa ningún patrón en una serie de mediciones repetidas, la presencia de errores sistemáticos fijos sólo se puede detectar si se comprueban las mediciones, ya sea midiendo una cantidad conocida o comparando las lecturas con las realizadas con un aparato diferente, que se sabe que es más preciso. Por ejemplo, si piensa en el tiempo de un péndulo utilizando un cronómetro preciso varias veces, obtendrá lecturas distribuidas aleatoriamente en torno a la media. El error sistemático de Hoping está presente si se compara el cronómetro con el " reloj parlante " del sistema telefónico y se descubre que va lento o rápido. Claramente, los tiempos del péndulo deben corregirse según lo rápido o lento que se descubra que va el cronómetro.
Los instrumentos de medición, como amperímetros y voltímetros, deben comprobarse periódicamente según estándares conocidos.
Los errores sistemáticos también se pueden detectar midiendo magnitudes ya conocidas. Por ejemplo, se puede comprobar un espectrómetro equipado con una rejilla de difracción midiendo con él la longitud de onda de las líneas D del espectro electromagnético del sodio , que se encuentran a 600 nm y 589,6 nm. Las mediciones se pueden utilizar para determinar el número de líneas por milímetro de la rejilla de difracción, que luego se puede utilizar para medir la longitud de onda de cualquier otra línea espectral.
Los errores sistemáticos constantes son muy difíciles de abordar, ya que sus efectos solo son observables si se pueden eliminar. Dichos errores no se pueden eliminar repitiendo mediciones o promediando un gran número de resultados. Un método común para eliminar el error sistemático es mediante la calibración del instrumento de medición.
El error aleatorio o estocástico en una medición es el error que es aleatorio de una medición a la siguiente. Los errores estocásticos tienden a distribuirse normalmente cuando el error estocástico es la suma de muchos errores aleatorios independientes debido al teorema del límite central . Los errores estocásticos agregados a una ecuación de regresión explican la variación en Y que no se puede explicar por las X incluidas .
El término "error de observación" también se utiliza a veces para referirse a errores de respuesta y otros tipos de errores ajenos al muestreo . [1] En situaciones de tipo encuesta, estos errores pueden ser errores en la recopilación de datos, incluyendo tanto el registro incorrecto de una respuesta como el registro correcto de la respuesta inexacta de un encuestado. Estas fuentes de error ajeno al muestreo se analizan en Salant y Dillman (1994) y Bland y Altman (1996). [4] [5]
Estos errores pueden ser aleatorios o sistemáticos. Los errores aleatorios son causados por errores no intencionados de los encuestados, entrevistadores y/o codificadores. El error sistemático puede ocurrir si hay una reacción sistemática de los encuestados al método utilizado para formular la pregunta de la encuesta. Por lo tanto, la formulación exacta de una pregunta de la encuesta es crucial, ya que afecta el nivel de error de medición. [6] Hay diferentes herramientas disponibles para los investigadores que los ayudan a decidir sobre esta formulación exacta de sus preguntas, por ejemplo, estimar la calidad de una pregunta utilizando experimentos MTMM . Esta información sobre la calidad también se puede utilizar para corregir el error de medición . [7] [8]
Si la variable dependiente en una regresión se mide con error, el análisis de regresión y las pruebas de hipótesis asociadas no se ven afectados, excepto que el R 2 será menor de lo que sería con una medición perfecta.
Sin embargo, si una o más variables independientes se miden con error, entonces los coeficientes de regresión y las pruebas de hipótesis estándar no son válidos. [9] Esto se conoce como sesgo de atenuación . [10]
El sesgo generado por este tipo de error de medición en los regresores se denomina sesgo de atenuación.