Sobre (matemáticas)

Familia de curvas en geometría.

Construcción de la envolvente de una familia de curvas.

En geometría , una envolvente de una familia plana de curvas es una curva que es tangente a cada miembro de la familia en algún punto, y estos puntos de tangencia juntos forman la envolvente completa. Clásicamente, se puede considerar un punto de la envolvente como la intersección de dos curvas " infinitamente adyacentes", es decir, el límite de las intersecciones de curvas cercanas. Esta idea se puede generalizar a una envoltura de superficies en el espacio, y así sucesivamente a dimensiones superiores.

Para tener una envolvente, es necesario que los miembros individuales de la familia de curvas sean curvas diferenciables ya que el concepto de tangencia no se aplica de otro modo, y tiene que haber una transición suave a través de los miembros. Pero estas condiciones no son suficientes: una determinada familia puede no tener un sobre. Un ejemplo sencillo de esto lo da una familia de círculos concéntricos de radio en expansión.

Envoltura de una familia de curvas.

Sea cada curva C _t de la familia como la solución de una ecuación f _t ( x ,  y ) = 0 (ver curva implícita ), donde t es un parámetro. Escriba F ( t ,  x ,  y ) = f _t ( x ,  y ) y suponga que F es diferenciable.

La envolvente de la familia C _t se define entonces como el conjunto de puntos ( x , y ) para los cuales, simultáneamente, ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0}$

para algún valor de t , donde es la derivada parcial de F con respecto a t . ^[1] ${\displaystyle \partial F/\partial t}$

Si t y u , t ≠ u son dos valores del parámetro, entonces la intersección de las curvas C _t y C _u viene dada por

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

o equivalente,

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.}$

Dejar u → t da la definición anterior.

Un caso especial importante es cuando F ( t ,  x ,  y ) es un polinomio en t . Esto incluye, limpiando denominadores , el caso en el que F ( t ,  x ,  y ) es una función racional en t . En este caso, la definición equivale a que t sea una raíz doble de F ( t ,  x ,  y ), por lo que la ecuación de la envolvente se puede encontrar estableciendo el discriminante de F en 0 (porque la definición exige F=0 en algún momento). t y primera derivada =0, ​​es decir, su valor 0 y es mínimo/máximo en ese t).

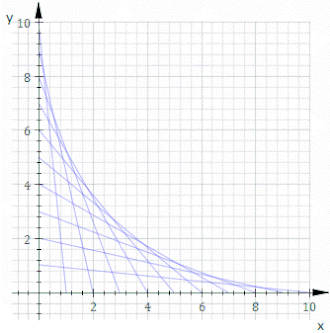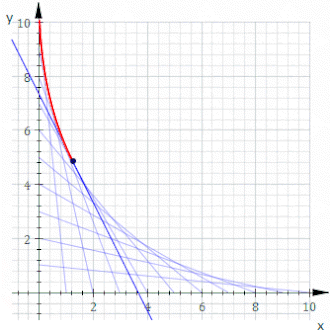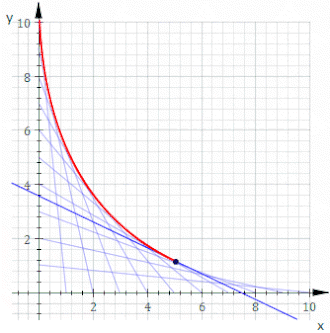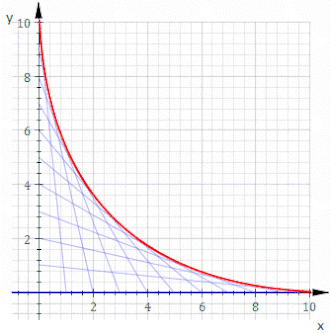
Por ejemplo, sea C _t la línea cuyas intersecciones xey son t y 11− t , esto se muestra en la animación anterior. La ecuación de C _t es

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

o, limpiando fracciones,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

La ecuación de la envolvente es entonces

${\displaystyle (-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,}$

A menudo, cuando F no es una función racional del parámetro, puede reducirse a este caso mediante una sustitución adecuada. Por ejemplo, si la familia está dada por C _θ con una ecuación de la forma u ( x ,  y )cos θ+ v ( x ,  y )sin θ= w ( x ,  y ), entonces poniendo t = e ^{i θ} , cos θ=( t +1/ t )/2, sin θ=( t -1/ t )/2 i cambia la ecuación de la curva a

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

o

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

La ecuación de la envolvente se obtiene estableciendo el discriminante en 0:

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

o

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Definiciones alternativas

1. La envolvente E ₁ es el límite de intersecciones de curvas cercanas C _t .
2. La envolvente E ₂ es una curva tangente a todos los C _t .
3. La envolvente E ₃ es el límite de la región ocupada por las curvas C _t .

Entonces , y , donde está el conjunto de puntos definidos al principio de la sección principal de esta subsección. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$

Ejemplos

Ejemplo 1

Estas definiciones E1 , E2 _y E3 de _la envolvente pueden ser conjuntos diferentes _. Considere, por ejemplo, la curva y = x ³ parametrizada por γ: R → R ² donde γ( t ) = ( t , t ³ ) . La familia de curvas de un parámetro estará dada por las rectas tangentes a γ.

Primero calculamos el discriminante . La función generadora es ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,(x,y))=3t^{2}x-y-2t^{3}.}$

Calcular la derivada parcial F _t = 6 t ( x – t ) . De ello se deduce que x = t o t = 0 . Primero suponga que x = t y t ≠ 0 . Sustituyendo en F: y así, suponiendo que t ≠ 0, se sigue que F = F _t = 0 si y sólo si ( x , y ) = ( t , t ³ ) . A continuación, suponiendo que t = 0 y sustituyendo en F se obtiene F (0,( x , y )) = − y . Entonces, suponiendo t = 0 , se deduce que F = F _t = 0 si y sólo si y = 0 . Por tanto, el discriminante es la curva original y su recta tangente en γ(0): ${\displaystyle F(t,(t,y))=t^{3}-y\,}$

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

A continuación calculamos E ₁ . Una curva está dada por F ( t ,( x , y )) = 0 y una curva cercana está dada por F ( t + ε,( x , y )) donde ε es un número muy pequeño. El punto de intersección surge al observar el límite de F ( t ,( x , y )) =  F ( t + ε,( x , y )) cuando ε tiende a cero. Observe que F ( t ,( x , y )) =  F ( t + ε,( x , y )) si y solo si

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Si t ≠ 0 entonces L tiene un solo factor de ε. Suponiendo que t ≠ 0 entonces la intersección viene dada por

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .}$

Como t ≠ 0 se sigue que x = t . El valor de y se calcula sabiendo que este punto debe estar en una línea tangente a la curva original γ: que F ( t ,( x , y )) = 0 . Sustituyendo y resolviendo se obtiene y = t ³ . Cuando t = 0 , L es divisible por ε ² . Suponiendo que t = 0 entonces la intersección viene dada por

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

Se deduce que x = 0 , y sabiendo que F ( t ,( x , y )) = 0 da y = 0 . Resulta que

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

A continuación calculamos E ₂ . La curva en sí es la curva que es tangente a todas sus rectas tangentes. Resulta que

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Finalmente calculamos E ₃ . Cada punto en el plano tiene al menos una línea tangente a γ que lo atraviesa, por lo que la región llena por las líneas tangentes es todo el plano. La frontera E ₃ es, por tanto, el conjunto vacío. De hecho, considere un punto en el plano, digamos ( x ₀ , y ₀ ). Este punto se encuentra en una recta tangente si y sólo si existe un t tal que

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

Esta es una cúbica en t y como tal tiene al menos una solución real. De ello se deduce que al menos una recta tangente a γ debe pasar por cualquier punto dado del plano. Si y > x ³ y y > 0 entonces cada punto ( x , y ) tiene exactamente una línea tangente a γ que lo atraviesa. Lo mismo ocurre si y < x ³ y < 0 . Si y < x ³ e y > 0 entonces cada punto ( x , y ) tiene exactamente tres rectas tangentes distintas a γ que lo atraviesan. Lo mismo ocurre si y > x ³ y y < 0 . Si y = x ³ e y ≠ 0 entonces cada punto ( x , y ) tiene exactamente dos rectas tangentes a γ que lo atraviesan (esto corresponde a que el cúbico tenga una raíz ordinaria y una raíz repetida). Lo mismo ocurre si y ≠ x ³ e y = 0 . Si y = x ³ y x = 0 , es decir, x = y = 0 , entonces este punto tiene una sola línea tangente a γ que lo atraviesa (esto corresponde a que la cúbica tenga una raíz real de multiplicidad 3). Resulta que

${\displaystyle E_{3}=\varnothing .}$

Ejemplo 2

Este gráfico da la envolvente de la familia de líneas que conectan puntos ( t ,0), (0, k - t ), en la que k toma el valor 1.

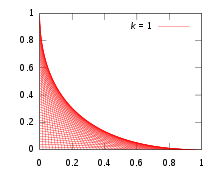
En el arte con cuerdas es común conectar dos líneas de pines equiespaciados. ¿Qué curva se forma?

Para simplificar, coloque los pasadores en los ejes x e y ; un diseño no ortogonal es una rotación y una reducción de escala . Un hilo de línea recta general conecta los dos puntos (0, k − t ) y ( t , 0), donde k es una constante de escala arbitraria, y la familia de líneas se genera variando el parámetro t . Desde geometría simple, la ecuación de esta línea recta es y = −( k  −  t ) x / t + k  −  t . Reorganizar y convertir en la forma F ( x , y , t ) = 0 da:

Ahora diferencia F ( x , y , t ) con respecto a t y establece el resultado igual a cero, para obtener

Estas dos ecuaciones definen conjuntamente la ecuación de la envolvente. De (2) tenemos:

${\displaystyle t={\sqrt {kx}}\,}$

Sustituyendo este valor de t en (1) y simplificando se obtiene una ecuación para la envolvente:

O, reorganizándolo en una forma más elegante que muestre la simetría entre xey:

Podemos tomar una rotación de los ejes donde el eje b es la línea y=x orientada al noreste y el eje a es la línea y =− x orientada al sureste. Estos nuevos ejes están relacionados con los ejes xy originales por x =( b + a )/ √ 2 y y =( b − a )/ √ 2 . Obtenemos, después de sustituir en (4) y expandir y simplificar,

que aparentemente es la ecuación de una parábola con eje a lo largo de a =0, ​​o y = x .

Ejemplo 3

Sea I ⊂ R un intervalo abierto y sea γ : I → R ² una curva plana suave parametrizada por la longitud del arco . Considere la familia de rectas normales de un parámetro a γ( I ). Una recta es normal a γ en γ( t ) si pasa por γ( t ) y es perpendicular al vector tangente a γ en γ( t ). Sea T el vector unitario tangente a γ y sea N el vector unitario normal . Usando un punto para denotar el producto escalar , la familia generadora de la familia de líneas normales de un parámetro viene dada por F  : I × R ² → R donde

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Claramente ( x − γ) · T = 0 si y solo si x − γ es perpendicular a T , o de manera equivalente, si y solo si x − γ es paralelo a N , o de manera equivalente, si y solo si x = γ + λ N para algunos λ ∈ R . Resulta que

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}}$

es exactamente la línea normal a γ en γ( t ₀ ). Para encontrar el discriminante de F necesitamos calcular su derivada parcial con respecto a t :

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,}$

donde κ es la curvatura plana de γ. Se ha visto que F = 0 si y sólo si x - γ = λ N para algún λ ∈ R . Suponiendo que F = 0 da

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

Suponiendo que κ ≠ 0 se deduce que λ = 1/κ y así

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

Esta es exactamente la evolución de la curva γ.

Ejemplo 4

Un astroide como envolvente de la familia de rectas que conectan los puntos ( s ,0 ), (0, t ) con s ²  +  t ²  = 1

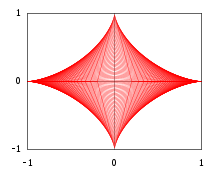
El siguiente ejemplo muestra que en algunos casos la envolvente de una familia de curvas puede verse como el límite topológico de una unión de conjuntos, cuyos límites son las curvas de la envolvente. Para y considere el triángulo rectángulo (abierto) en un plano cartesiano con vértices , y ${\displaystyle s>0}$ ${\displaystyle t>0}$ ${\displaystyle (0,0)}$ ${\displaystyle (s,0)}$ ${\displaystyle (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.}$

Fijar un exponente y considerar la unión de todos los triángulos sujetos a la restricción , es decir el conjunto abierto ${\displaystyle \alpha >0}$ ${\displaystyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Para escribir una representación cartesiana de , comience con cualquiera , satisfactorio y cualquiera . La desigualdad de Hölder con respecto a los exponentes conjugados da : ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle s>0}$ ${\displaystyle \textstyle t>0}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$ ${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \mathbb {R} ^{2}}$ ${\displaystyle p:=1+{\frac {1}{\alpha }}}$ ${\displaystyle \textstyle q:={1+\alpha }}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}}$,

con igualdad si y sólo si . En términos de una unión de conjuntos, la última desigualdad dice: el punto pertenece al conjunto , es decir, pertenece a alguno con , si y sólo si satisface ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$ ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

Además, el límite del conjunto es la envolvente de la correspondiente familia de segmentos de recta. ${\displaystyle \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(es decir, las hipotenusas de los triángulos), y tiene ecuación cartesiana

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

Observe que, en particular, el valor da el arco de parábola del ejemplo 2, y el valor (lo que significa que todas las hipotenusas son segmentos de longitud unitaria) da el astroide . ${\displaystyle \alpha =1}$ ${\displaystyle \alpha =2}$

Ejemplo 5

La envolvente de las órbitas de los proyectiles (con velocidad inicial constante) es una parábola cóncava. La velocidad inicial es de 10 m/s. Tomamos g = 10 m/s ² .

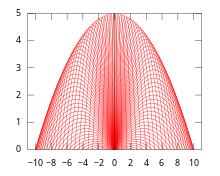
Consideremos el siguiente ejemplo de envolvente en movimiento. Supongamos que a una altura inicial 0, se lanza un proyectil al aire con velocidad inicial constante v pero con diferentes ángulos de elevación θ. Sea x el eje horizontal en la superficie de movimiento y sea y el eje vertical. Entonces el movimiento da el siguiente sistema dinámico diferencial :

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,}$

que satisface cuatro condiciones iniciales :

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Aquí t denota el tiempo de movimiento, θ es el ángulo de elevación, g denota aceleración gravitacional y v es la velocidad inicial constante (no la velocidad ). La solución del sistema anterior puede tomar una forma implícita :

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.}$

Para encontrar su ecuación envolvente, se puede calcular la derivada deseada:

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

Eliminando θ, se puede llegar a la siguiente ecuación envolvente:

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Claramente la envolvente resultante también es una parábola cóncava .

Envoltura de una familia de superficies.

Una familia de superficies de un parámetro en el espacio euclidiano tridimensional está dada por un conjunto de ecuaciones

${\displaystyle F(x,y,z,a)=0}$

dependiendo de un parámetro real a . ^[2] Por ejemplo, los planos tangentes a una superficie a lo largo de una curva en la superficie forman dicha familia.

Dos superficies correspondientes a diferentes valores a y a' se cruzan en una curva común definida por

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.}$

En el límite, cuando a' se acerca a a , esta curva tiende a una curva contenida en la superficie en un

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Esta curva se llama característica de la familia en a . A medida que varía el lugar geométrico de estas curvas características, se define una superficie llamada envolvente de la familia de superficies.

La envolvente de una familia de superficies es tangente a cada superficie de la familia a lo largo de la curva característica de esa superficie.

Generalizaciones

La idea de una envolvente de una familia de subvariedades suaves se desprende naturalmente. En general, si tenemos una familia de subvariedades con codimensión c, entonces necesitamos tener al menos una familia de parámetros c de dichas subvariedades. Por ejemplo: una familia de curvas de un parámetro en tres espacios ( c = 2) no tiene, genéricamente, envolvente.

Aplicaciones

Ecuaciones diferenciales ordinarias

Las envolventes están relacionadas con el estudio de ecuaciones diferenciales ordinarias (EDO) y, en particular, soluciones singulares de EDO. ^[3] Considere, por ejemplo, la familia de rectas tangentes de un parámetro a la parábola y = x ² . Estos están dados por la familia generadora F ( t ,( x , y )) = t ² – 2 tx + y . El conjunto de nivel cero F ( t ₀ ,( x , y )) = 0 da la ecuación de la recta tangente a la parábola en el punto ( t ₀ , t ₀ ² ). La ecuación t ² – 2 tx + y = 0 siempre se puede resolver para y en función de x , por lo que considere

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

Sustituyendo

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

da la ODA

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

No sorprende que y  = 2 tx  −  t ² sean todas soluciones de esta EDO. Sin embargo, la envolvente de esta familia de rectas de un parámetro, que es la parábola y  =  x ² , también es una solución para esta EDO. Otro ejemplo famoso es la ecuación de Clairaut .

Ecuaciones diferenciales parciales

Las envolventes se pueden utilizar para construir soluciones más complicadas de ecuaciones diferenciales parciales (PDE) de primer orden a partir de otras más simples. ^[4] Sea F ( x , u ,D u ) = 0 una PDE de primer orden, donde x es una variable con valores en un conjunto abierto Ω ⊂  R ⁿ , u es una función de valor real desconocida, D u es la gradiente de u , y F es una función continuamente diferenciable que es regular en D u . Supongamos que u ( x ; a ) es una familia de soluciones de m -parámetros: es decir, para cada a  ∈  A  ⊂  R ^m fijo , u ( x ; a ) es una solución de la ecuación diferencial. Se puede construir una nueva solución de la ecuación diferencial resolviendo primero (si es posible)

${\displaystyle D_{a}u(x;a)=0\,}$

para a  = φ( x ) en función de x . La envolvente de la familia de funciones { u (·, a )} _{a ∈ A} está definida por

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

y también resuelve la ecuación diferencial (siempre que exista como una función continuamente diferenciable).

Geométricamente, la gráfica de v ( x ) es tangente en todas partes a la gráfica de algún miembro de la familia u ( x ; a ). Dado que la ecuación diferencial es de primer orden, solo impone una condición en el plano tangente a la gráfica, de modo que cualquier función en todas partes tangente a una solución también debe ser una solución. La misma idea subyace a la solución de una ecuación de primer orden como integral del cono de Monge . ^[5] El cono de Monge es un campo de cono en el R ^{n +1} de las variables ( x , u ) recortadas por la envolvente de los espacios tangentes a la PDE de primer orden en cada punto. Una solución de la PDE es entonces una envolvente del campo de conos.

En geometría de Riemann , si una familia suave de geodésicas que pasa por un punto P en una variedad de Riemann tiene una envolvente, entonces P tiene un punto conjugado donde cualquier geodésica de la familia intersecta la envolvente. Lo mismo es cierto de manera más general en el cálculo de variaciones : si una familia de extremos a un funcional que pasa por un punto dado P tiene una envolvente, entonces un punto donde un extremo intersecta la envolvente es un punto conjugado de P.

Cáusticos

Cáustica reflectante generada a partir de un círculo y rayos paralelos.

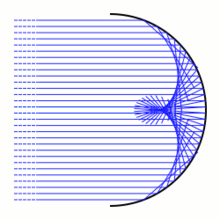
En óptica geométrica , una cáustica es la envoltura de una familia de rayos luminosos . En esta imagen hay un arco de círculo. Los rayos de luz (que se muestran en azul) provienen de una fuente en el infinito y, por lo tanto, llegan en paralelo. Cuando inciden en el arco circular, los rayos de luz se dispersan en diferentes direcciones según la ley de la reflexión . Cuando un rayo de luz incide en el arco en un punto, la luz se reflejará como si hubiera sido reflejada por la línea tangente del arco en ese punto. Los rayos de luz reflejados dan una familia de líneas de un parámetro en el plano. La envoltura de estas líneas es la cáustica reflectante . Una cáustica reflectante constará genéricamente de puntas lisas y puntas de cúspide ordinarias .

Desde el punto de vista del cálculo de variaciones, el principio de Fermat (en su forma moderna) implica que los rayos de luz son los extremos de la longitud funcional.

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

entre curvas suaves γ en [ a , b ] con puntos finales fijos γ( a ) y γ( b ). La cáustica determinada por un punto dado P (en la imagen el punto está en el infinito) es el conjunto de puntos conjugados a P . ^[6]

principio de huygens

La luz puede pasar a través de medios anisotrópicos no homogéneos a diferentes velocidades dependiendo de la dirección y la posición inicial del rayo de luz. El límite del conjunto de puntos a los que puede viajar la luz desde un punto dado q después de un tiempo t se conoce como frente de onda después del tiempo t , denotado aquí por Φ _q ( t ). Consiste precisamente en los puntos a los que se puede llegar desde q en el tiempo t viajando a la velocidad de la luz. El principio de Huygens afirma que el conjunto de frentes de onda Φ _{q 0} ( s + t ) es la envolvente de la familia de frentes de onda Φ _q ( s ) para q  ∈ Φ _{q 0} ( t ). De manera más general, el punto q ₀ podría ser reemplazado por cualquier curva, superficie o conjunto cerrado en el espacio. ^[7]

Ver también

• Cáustico (matemáticas)
• Teorema de la envolvente
• Superficie reglada

Referencias

1. Bruce, JW; Giblin, PJ (1984), Curvas y singularidades , Cambridge University Press, ISBN 0-521-42999-4
2. Eisenhart, Luther P. (2008), Tratado sobre la geometría diferencial de curvas y superficies , Schwarz Press, ISBN 1-4437-3160-9
3. Forsyth, Andrew Russell (1959), Teoría de las ecuaciones diferenciales , Seis volúmenes encuadernados en tres, Nueva York: Dover Publications , MR  0123757, §§100-106.
4. Evans, Lawrence C. (1998), Ecuaciones diferenciales parciales , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9.
5. John, Fritz (1991), Ecuaciones diferenciales parciales (4ª ed.), Springer, ISBN 978-0-387-90609-6.
6. Born, Max (octubre de 1999), Principio de la óptica , Cambridge University Press , ISBN 978-0-521-64222-4, Apéndice I: El cálculo de variaciones.
7. Arnold, VI (1997), Métodos matemáticos de la mecánica clásica, 2ª ed. , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-96890-2, §46.

enlaces externos

• Weisstein, Eric W. "Sobre". MundoMatemático .
• "Envolvente de una familia de curvas planas" en MathCurve.