En matemáticas , la red de subgrupos de un grupo es la red cuyos elementos son los subgrupos de , siendo el ordenamiento parcial la inclusión . En esta red, la unión de dos subgrupos es el subgrupo generado por su unión , y la unión de dos subgrupos es su intersección .
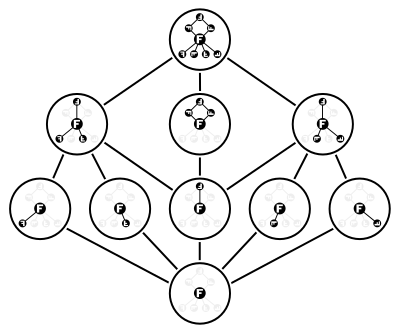
El grupo diédrico Dih 4 tiene diez subgrupos, contándose a sí mismo y al subgrupo trivial . Cinco de los ocho elementos del grupo generan subgrupos de orden dos, y los otros dos elementos no identidad generan el mismo subgrupo cíclico de orden cuatro. Además, hay dos subgrupos de la forma Z 2 × Z 2 , generados por pares de elementos de orden -dos . En la ilustración se muestra la red formada por estos diez subgrupos.
Este ejemplo también muestra que la red de todos los subgrupos de un grupo no es una red modular en general. De hecho, esta red particular contiene el "pentágono" prohibido N 5 como subred .
Para cualquier subgrupo A , B y C de un grupo con A ≤ C ( A un subgrupo de C ), entonces AB ∩ C = A ( B ∩ C ); la multiplicación aquí es el producto de subgrupos . Esta propiedad se ha denominado propiedad modular de los grupos (Aschbacher 2000) o ley modular ( de Dedekind ) (Robinson 1996, Cohn 2000). Dado que para dos subgrupos normales el producto es en realidad el subgrupo más pequeño que contiene a los dos, los subgrupos normales forman una red modular .
El teorema de la red establece una conexión de Galois entre la red de subgrupos de un grupo y la de sus cocientes .
El lema de Zassenhaus da un isomorfismo entre ciertas combinaciones de cocientes y productos en la red de subgrupos.
En general, no hay restricción sobre la forma de la red de subgrupos, en el sentido de que cada red es isomorfa a una subred de la red de subgrupos de algún grupo. Además, cada red finita es isomorfa a una subred de la red de subgrupo de algún grupo finito (Schmidt 1994, p. 9). Cada red distributiva finita también es isomorfa a la red de subgrupos normal de algún grupo (Silcock 1977).
Los subgrupos con ciertas propiedades forman redes, pero otras propiedades no.
Sin embargo, ni los subgrupos finitos ni los subgrupos de torsión forman una red: por ejemplo, el producto libre es generado por dos elementos de torsión , pero es infinito y contiene elementos de orden infinito.
El hecho de que los subgrupos normales formen una red modular es un caso particular de un resultado más general, a saber, que en cualquier variedad de Maltsev (de la cual los grupos son un ejemplo), la red de congruencias es modular (Kearnes y Kiss 2013).
La información teórica de la red sobre la red de subgrupos a veces se puede utilizar para inferir información sobre el grupo original, una idea que se remonta al trabajo de Øystein Ore (1937, 1938). Por ejemplo, como demostró Ore , un grupo es localmente cíclico si y sólo si su red de subgrupos es distributiva . Si además la red satisface la condición de cadena ascendente , entonces el grupo es cíclico.
Los grupos cuya red de subgrupos es una red complementada se denominan grupos complementados (Zacher 1953), y los grupos cuya red de subgrupos son redes modulares se denominan grupos de Iwasawa o grupos modulares (Iwasawa 1941). También existen caracterizaciones teóricas de celosías de este tipo para grupos solubles y grupos perfectos (Suzuki 1951).