Teorema de Legendre sobre triángulos esféricos

En geometría , el teorema de Legendre sobre los triángulos esféricos , que lleva el nombre de Adrien-Marie Legendre , se enuncia de la siguiente manera:

Sea ABC un triángulo esférico en la esfera unitaria con lados pequeños a , b , c . Sea A'B'C' el triángulo plano con los mismos lados. Entonces los ángulos del triángulo esférico exceden los ángulos correspondientes del triángulo plano en aproximadamente un tercio del exceso esférico (el exceso esférico es la cantidad en la que la suma de los tres ángulos excede a π ).

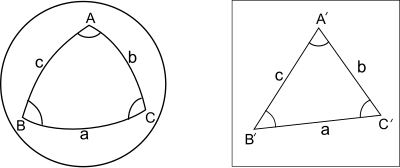
El teorema fue muy importante para simplificar el pesado trabajo numérico de calcular los resultados de los estudios geodésicos tradicionales (anteriores al GPS y a la computadora) desde aproximadamente 1800 hasta mediados del siglo XX.

El teorema fue expuesto por Legendre (1787), quien proporcionó una prueba (1798) en un suplemento al informe de la medición del arco meridional francés utilizado en la definición del metro (Delambre 1798) . Legendre no afirma que él fuera el creador del teorema a pesar de que se le atribuye. Tropfke (1903) sostiene que el método era de uso común entre los topógrafos de la época y puede haber sido utilizado ya en 1740 por La Condamine para el cálculo del arco meridional peruano .error de harv: sin destino: CITEREFDelambre1798 ( ayuda )

El teorema de Girard establece que el exceso esférico de un triángulo, E , es igual a su área, Δ, y por lo tanto el teorema de Legendre puede escribirse como

${\displaystyle {\begin{aligned}A-A'\;\approx \;B-B'\;\approx \;C-C'\;\approx \;{\frac {1}{3}}E\;=\;{\frac {1}{3}}\Delta ,\qquad a,\;b,\;c\,\ll \,1.\end{aligned}}}$

El exceso o área de los triángulos pequeños es muy pequeño. Por ejemplo, consideremos un triángulo esférico equilátero con lados de 60 km en una Tierra esférica de radio 6371 km; el lado corresponde a una distancia angular de 60/6371=.0094, o aproximadamente 10 ⁻² radianes (subtendiendo un ángulo de 0,57° en el centro). El área de un triángulo tan pequeño se aproxima bien a la de un triángulo equilátero plano con los mismos lados: 1 ⁄ 2 a ² sin ( π /3) = 0,0000433 radianes correspondientes a 8,9 ″.

Cuando los lados de los triángulos superen los 180 km, cuyo exceso sea de unas 80”, las relaciones entre las áreas y las diferencias de los ángulos deberán corregirse por términos de cuarto orden en los lados, que no sumen más de 0,01”:

${\displaystyle {\begin{aligned}\Delta &=\Delta '\left(1+{\frac {a^{2}+b^{2}+c^{2}}{24}}\right),\\A&=A'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left(-2a^{2}+b^{2}+c^{2}\right),\\B&=B'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}-2b^{2}+c^{2}}\right),\\C&=C'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}+b^{2}-2c^{2}}\right).\end{aligned}}}$

(Δ′ es el área del triángulo plano). Este resultado fue demostrado por Buzengeiger (1818); se puede encontrar una prueba ampliada en Osborne (2013) (Apéndice D13). Nádeník (2004) examina otros resultados.

El teorema se puede extender al elipsoide si a , b , c se calculan dividiendo las longitudes verdaderas por la raíz cuadrada del producto de los radios principales de curvatura (ver Osborne (2013) Capítulo 5) en la latitud media de los vértices. (en lugar de un radio esférico). Gauss (1828, art. 26-28) proporcionó fórmulas más exactas.

Referencias

• Buzengeiger, Karl Heribert Ignatz (1818), "Vergleichung zweier kleiner Dreiecke von gleichen Seiten, wovon das eine sphärisch, das andere eben ist", Zeitschrift für Astronomie und verwandte Wissenschaften , 6 : 264–270
• Clarke, Alexander Ross (1880), Geodesia, Clarendon Press
• Gauss, CF (1902) [1828]. Investigaciones generales de superficies curvas de 1827 y 1825. Universidad de Princeton. Lib. Traducción al inglés de Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828). {{cite book}}: Enlace externo en |postscript=( ayuda )Mantenimiento CS1: posdata ( enlace )
• Legendre, Adrien-Marie (1787), Mémoire sur les opérations trigonométriques, dont les résultats dépendant de la figure de la Terre, p. 7 (Artículo VI [1])
• Legendre, Adrien-Marie (1798), Méthode pour déterminer la longueur exactitude du quart du méridien d'après les comments faites pour la mesure de l'arc compris entre Dunkerque et Barcelone, págs. 12-14 (Nota III [2])
• Nádeník, Zbynek (2004), Teorema de Legendre sobre triángulos esféricos (PDF) , archivado desde el original (PDF) el 16 de enero de 2014
• Osborne, Peter (2013), The Mercator Projections, archivado desde el original el 24 de septiembre de 2013.
• Tropfke, Johannes (1903), Geschichte der Elementar-Mathematik (Volumen 2), Verlag von Veit, p. 295