
En geometría , el teorema de Brahmagupta establece que si un cuadrilátero cíclico es ortodiagonal (es decir, tiene diagonales perpendiculares ), entonces la perpendicular a un lado desde el punto de intersección de las diagonales siempre biseca al lado opuesto. [1] Recibe su nombre en honor al matemático indio Brahmagupta (598-668). [2]
Más específicamente, sean A , B , C y D cuatro puntos en un círculo tales que las líneas AC y BD son perpendiculares. Denotemos la intersección de AC y BD por M. Elevemos la perpendicular desde M a la línea BC , llamando a la intersección E. Sea F la intersección de la línea EM y la arista AD . Entonces, el teorema establece que F es el punto medio AD .
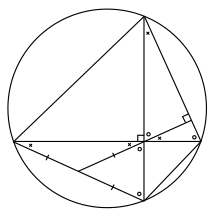
Necesitamos demostrar que AF = FD . Probaremos que tanto AF como FD son, de hecho, iguales a FM .
Para demostrar que AF = FM , primero hay que tener en cuenta que los ángulos FAM y CBM son iguales, porque son ángulos inscritos que interceptan el mismo arco de círculo (CD). Además, los ángulos CBM y CME son ambos complementarios del ángulo BCM (es decir, suman 90°) y, por lo tanto, son iguales. Por último, los ángulos CME y FMA son iguales. Por lo tanto, AFM es un triángulo isósceles y, por lo tanto, los lados AF y FM son iguales.
La prueba de que FD = FM es similar: los ángulos FDM , BCM , BME y DMF son todos iguales, por lo que DFM es un triángulo isósceles, por lo que FD = FM . De ello se deduce que AF = FD , como afirma el teorema.