El problema de la localización de puntos es un tema fundamental de la geometría computacional . Tiene aplicaciones en áreas que tratan el procesamiento de datos geométricos: gráficos por computadora , sistemas de información geográfica (GIS), planificación de movimiento y diseño asistido por computadora (CAD).
En su forma más general, el problema consiste en determinar la región en la que se encuentra un punto de consulta, dada una partición del espacio en regiones disjuntas . Por ejemplo, el problema de determinar qué ventana de una interfaz gráfica de usuario contiene un clic del ratón determinado se puede formular como una instancia de ubicación de puntos, con una subdivisión formada por las partes visibles de cada ventana, aunque las estructuras de datos especializadas pueden ser más apropiadas que las estructuras de datos de ubicación de puntos de propósito general en esta aplicación. [1] Otro caso especial es el problema del punto en el polígono , en el que se necesita determinar si un punto está dentro, fuera o en el límite de un único polígono .
En muchas aplicaciones, es necesario determinar la ubicación de varios puntos diferentes con respecto a la misma partición del espacio. Para resolver este problema de manera eficiente, es útil construir una estructura de datos que, dado un punto de consulta, determine rápidamente qué región contiene el punto de consulta (por ejemplo, un diagrama de Voronoi ).

En el caso planar, se nos da una subdivisión planar S , formada por múltiples polígonos llamados caras, y necesitamos determinar qué cara contiene un punto de consulta. Una búsqueda de fuerza bruta de cada cara usando el algoritmo de punto en polígono es posible, pero generalmente no es factible para subdivisiones de alta complejidad. Varios enfoques diferentes conducen a estructuras de datos óptimas, con O ( n ) espacio de almacenamiento y O(log n ) tiempo de consulta, donde n es el número total de vértices en S . Para simplificar, asumimos que la subdivisión planar está contenida dentro de un cuadro delimitador cuadrado.

La estructura de datos más simple y antigua para lograr un tiempo O(log n ) fue descubierta por Dobkin y Lipton en 1976. Se basa en subdividir S utilizando líneas verticales que pasan por cada vértice en S . La región entre dos líneas verticales consecutivas se llama losa . Observe que cada losa está dividida por segmentos de línea que no se intersecan y que cruzan completamente la losa de izquierda a derecha. La región entre dos segmentos consecutivos dentro de una losa corresponde a una cara única de S . Por lo tanto, reducimos nuestro problema de ubicación de puntos a dos problemas más simples: [2]
El primer problema se puede resolver mediante una búsqueda binaria en la coordenada x de las líneas verticales en tiempo O(log n ). El segundo problema también se puede resolver en tiempo O(log n ) mediante una búsqueda binaria. Para ver cómo, observe que, como los segmentos no se intersecan ni cruzan completamente la placa, los segmentos se pueden ordenar verticalmente dentro de cada placa. Si bien este algoritmo permite la ubicación de puntos en tiempo logarítmico y es fácil de implementar, el espacio requerido para construir las placas y las regiones contenidas dentro de las placas puede ser tan alto como O( n ²), ya que cada placa puede cruzar una fracción significativa de los segmentos. [2]
Varios autores notaron que los segmentos que cruzan dos losas adyacentes son en su mayoría iguales. Por lo tanto, el tamaño de la estructura de datos se puede reducir significativamente. Más específicamente, Sarnak y Tarjan trazan una línea vertical l de izquierda a derecha sobre el plano, mientras mantienen los segmentos que intersecan l en un árbol rojo-negro persistente . Esto les permite reducir el espacio de almacenamiento a O( n ), mientras mantienen el tiempo de consulta O(log n ). [3]

Una cadena monótona (vertical) es un camino tal que la coordenada y nunca aumenta a lo largo del camino. Un polígono simple es monótono (vertical) si está formado por dos cadenas monótonas, con el primer y último vértice en común. Es posible agregar algunas aristas a una subdivisión plana, para hacer que todas las caras sean monótonas, obteniendo lo que se llama una subdivisión monótona. Este proceso no agrega ningún vértice a la subdivisión (por lo tanto, el tamaño permanece O( n )), y se puede realizar en tiempo O( n log n ) por barrido plano (también se puede realizar en tiempo lineal, utilizando triangulación de polígonos ). Por lo tanto, no hay pérdida de generalidad, si restringimos nuestra estructura de datos al caso de subdivisiones monótonas, como lo hacemos en esta sección.
La debilidad de la descomposición en losas es que las líneas verticales crean segmentos adicionales en la descomposición, lo que dificulta lograr un espacio de almacenamiento O( n ). Herbert Edelsbrunner , Leonidas J. Guibas y Jorge Stolfi descubrieron una estructura de datos óptima que solo utiliza los bordes en una subdivisión monótona. La idea es utilizar cadenas monótonas verticales, en lugar de utilizar líneas verticales para dividir la subdivisión. [4]
Convertir esta idea general en una estructura de datos eficiente no es una tarea sencilla. En primer lugar, debemos ser capaces de calcular una cadena monótona que divida la subdivisión en dos mitades de tamaños similares. En segundo lugar, dado que algunas aristas pueden estar contenidas en varias cadenas monótonas, debemos tener cuidado de garantizar que el espacio de almacenamiento sea O(n). En tercer lugar, comprobar si un punto está en el lado izquierdo o derecho de una subdivisión monótona lleva O( n ) tiempo si se realiza de forma ingenua. [4]
Los detalles sobre cómo resolver los dos primeros problemas están fuera del alcance de este artículo. Mencionamos brevemente cómo abordar el tercer problema. Usando la búsqueda binaria, podemos probar si un punto está a la izquierda o derecha de una cadena monótona en tiempo O(log n ). Como necesitamos realizar otra búsqueda binaria anidada a través de cadenas O(log n ) para determinar realmente la ubicación del punto, el tiempo de consulta es O(log² n). Para lograr un tiempo de consulta O(log n ), necesitamos usar cascada fraccionaria , manteniendo punteros entre los bordes de diferentes cadenas monótonas. [4]
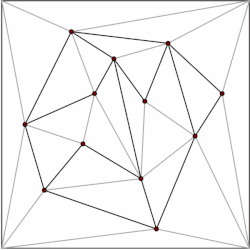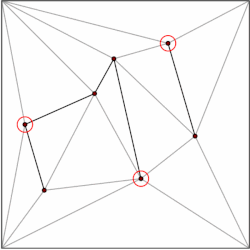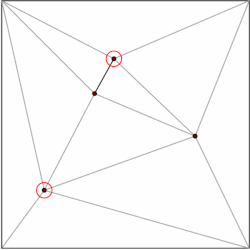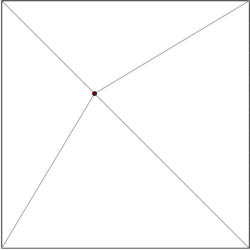
Un polígono con m vértices se puede dividir en m –2 triángulos, lo que se puede demostrar por inducción a partir de un triángulo. Existen numerosos algoritmos para triangular un polígono de manera eficiente, siendo el más rápido el que tiene un tiempo de O( n ) en el peor de los casos. Por lo tanto, podemos descomponer cada polígono de nuestra subdivisión en triángulos y restringir nuestra estructura de datos al caso de subdivisiones formadas exclusivamente por triángulos. Kirkpatrick proporciona una estructura de datos para la ubicación de puntos en subdivisiones trianguladas con espacio de almacenamiento O( n ) y tiempo de consulta O(log n ). [5]
La idea general es construir una jerarquía de triángulos. Para realizar una consulta, comenzamos por encontrar el triángulo de nivel superior que contiene el punto de consulta. Dado que el número de triángulos de nivel superior está limitado por una constante, esta operación se puede realizar en tiempo O(1). Cada triángulo tiene punteros a los triángulos que interseca en el siguiente nivel de la jerarquía, y el número de punteros también está limitado por una constante. Procedemos con la consulta encontrando qué triángulo contiene el punto de consulta nivel por nivel. [5]
La estructura de datos se construye en el orden opuesto, es decir, de abajo hacia arriba. Comenzamos con la subdivisión triangulada y elegimos un conjunto independiente de vértices para eliminar. Después de eliminar los vértices, volvemos a triangular la subdivisión. Debido a que la subdivisión está formada por triángulos, un algoritmo voraz puede encontrar un conjunto independiente que contenga una fracción constante de los vértices. Por lo tanto, el número de pasos de eliminación es O(log n ). [5]

Un enfoque aleatorio para este problema se basa en la descomposición trapezoidal, o mapa trapezoidal. Una descomposición trapezoidal se obtiene disparando balas verticales que van hacia arriba y hacia abajo desde cada vértice en la subdivisión original. Las balas se detienen cuando golpean un borde y forman un nuevo borde en la subdivisión. De esta manera, obtenemos un subconjunto de la descomposición en losa, con solo O( n ) bordes y vértices, ya que para cada vértice en la subdivisión original solo agregamos dos nuevos vértices y aumentamos el número de bordes en cuatro. [6]
Una descomposición trapezoidal se puede construir añadiendo los segmentos de la subdivisión original, uno por uno, en un orden aleatorio. Inicialmente (antes de que no se hayan añadido segmentos) la descomposición trapezoidal consta de un solo trapezoide, el cuadro delimitador de la subdivisión. Cada paso posterior utiliza una consulta de ubicación de puntos para localizar un punto final del siguiente segmento de línea, dentro de la descomposición trapezoidal actual, y luego recorre desde el trapezoide resultante hasta los trapecios vecinos que contienen el mismo segmento, subdividándolos y recombinándolos para formar la descomposición refinada. El análisis inverso, una forma de análisis que se utiliza habitualmente para este tipo de algoritmo de geometría incremental aleatoria, muestra que el número esperado de trapecios creados para cada inserción está limitado por una constante y, por lo tanto, que el número total de pasos de este algoritmo, fuera de las ubicaciones de los puntos, es lineal. [6]
Las localizaciones de puntos en la subdivisión actual, realizadas dentro de este algoritmo, pueden realizarse utilizando la misma estructura que, al final del algoritmo, puede utilizarse para las consultas de localización de puntos en la descomposición trapezoidal final. Esta estructura de datos de localización de puntos toma la forma de un grafo acíclico dirigido , donde los vértices son los trapecios que existían en algún punto del refinamiento, y los bordes dirigidos conectan cada trapecio que ya no está en el refinamiento con los trapecios que lo reemplazaron. Una consulta de localización de puntos se realiza siguiendo una ruta en este grafo, comenzando desde el trapecio inicial, y en cada paso eligiendo el trapecio de reemplazo que contiene el punto de consulta, hasta llegar a un trapecio que no ha sido reemplazado. La profundidad esperada de una búsqueda en este dígrafo, comenzando desde cualquier punto de consulta, es O(log n ). El espacio para la estructura de datos es proporcional al número de trapecios creados a lo largo de este proceso de refinamiento, que en expectativa es O( n ). [6]
No se conocen estructuras de datos de ubicación de puntos generales con espacio lineal y tiempo de consulta logarítmico para dimensiones mayores que 2 [ cita requerida ] . Por lo tanto, necesitamos sacrificar tiempo de consulta o espacio de almacenamiento, o restringirnos a algún tipo de subdivisión menos general.
En el espacio tridimensional, es posible responder a consultas de ubicación de puntos en O(log² n ) utilizando el espacio O( n log n ). La idea general es mantener varias estructuras de datos de ubicación de puntos planares, correspondientes a la intersección de la subdivisión con n planos paralelos que contienen cada vértice de la subdivisión. Un uso ingenuo de esta idea aumentaría el espacio de almacenamiento a O( n ² ). De la misma manera que en la descomposición en losas, la similitud entre estructuras de datos consecutivas se puede explotar para reducir el espacio de almacenamiento a O( n log n ), pero el tiempo de consulta aumenta a O(log² n ). [7]
En un espacio de dimensión d , la ubicación de puntos se puede resolver proyectando recursivamente las caras en un espacio de dimensión ( d -1). Si bien el tiempo de consulta es O(log n ), el espacio de almacenamiento puede ser tan alto como . La alta complejidad de las estructuras de datos de dimensión d condujo al estudio de tipos especiales de subdivisión.
Un ejemplo importante es el caso de los arreglos de hiperplanos . Un arreglo de n hiperplanos define O( n d ) celdas, pero la localización de puntos se puede realizar en tiempo O(log n ) con espacio O( n d ) utilizando los cortes jerárquicos de Chazelle .
Otro tipo especial de subdivisión se denomina subdivisión rectilínea (u ortogonal). En una subdivisión rectilínea, todos los bordes son paralelos a uno de los ejes ortogonales d . En este caso, la ubicación del punto se puede responder en tiempo O(log d -1 n ) con espacio O( n ).