En informática , la cascada fraccionaria es una técnica para acelerar una secuencia de búsquedas binarias del mismo valor en una secuencia de estructuras de datos relacionadas. La primera búsqueda binaria en la secuencia toma una cantidad de tiempo logarítmica, como es estándar para las búsquedas binarias, pero las búsquedas sucesivas en la secuencia son más rápidas. La versión original de la cascada fraccionaria, introducida en dos artículos por Chazelle y Guibas en 1986 (Chazelle y Guibas 1986a; Chazelle y Guibas 1986b), combinó la idea de la cascada, originada en las estructuras de datos de búsqueda de rango de Lueker (1978) y Willard (1978), con la idea del muestreo fraccionario, que se originó en Chazelle (1983). Autores posteriores introdujeron formas más complejas de cascada fraccionaria que permiten que la estructura de datos se mantenga a medida que los datos cambian mediante una secuencia de eventos discretos de inserción y eliminación.
Como ejemplo simple de cascada fraccionaria, considere el siguiente problema. Se nos da como entrada una colección de listas ordenadas de números, de modo que la longitud total de todas las listas es , y debemos procesarlas para poder realizar búsquedas binarias de un valor de consulta en cada una de las listas. Por ejemplo, con y ,
La solución más sencilla para este problema de búsqueda es simplemente almacenar cada lista por separado. Si lo hacemos así, el requisito de espacio es , pero el tiempo para realizar una consulta es , ya que debemos realizar una búsqueda binaria independiente en cada una de las listas. El peor caso para consultar esta estructura se produce cuando cada una de las listas tiene el mismo tamaño , por lo que cada una de las búsquedas binarias involucradas en una consulta lleva tiempo .
Una segunda solución permite consultas más rápidas a costa de más espacio: podemos fusionar todas las listas en una única lista grande y asociar con cada elemento de una lista los resultados de la búsqueda de en cada una de las listas más pequeñas . Si describimos un elemento de esta lista fusionada como donde es el valor numérico y , , , y son las posiciones (el primer número tiene la posición 0) del siguiente elemento al menos tan grande como en cada una de las listas de entrada originales (o la posición después del final de la lista si no existe dicho elemento), entonces tendríamos
Esta solución fusionada permite una consulta en el tiempo : simplemente busque en y luego informe los resultados almacenados en el elemento encontrado por esta búsqueda. Por ejemplo, si , al buscar en se encuentra el elemento 62[1,3,2,3], del cual devolvemos los resultados , (un valor de bandera que indica que está más allá del final de ), , y . Sin embargo, esta solución paga una alta penalización en complejidad de espacio: usa espacio ya que cada uno de los elementos en debe almacenar una lista de resultados de búsqueda.
La cascada fraccionaria permite resolver este mismo problema de búsqueda con límites de tiempo y espacio que satisfacen lo mejor de ambos mundos: tiempo de consulta y espacio . La solución de la cascada fraccionaria es almacenar una nueva secuencia de listas . La lista final de esta secuencia, , es igual a ; cada lista anterior se forma fusionando con cada segundo elemento de . Con cada elemento de esta lista fusionada, almacenamos dos números: la posición resultante de la búsqueda en y la posición resultante de la búsqueda en . Para los datos anteriores, esto nos daría las siguientes listas:
Supongamos que deseamos realizar una consulta en esta estructura, para . Primero hacemos una búsqueda binaria estándar para in , encontrando el valor 64 [1,5]. El "1" en 64[1,5], nos dice que la búsqueda para in debe devolver . El "5" en 64 [1,5] nos dice que la ubicación aproximada de in es la posición 5. Más precisamente, la búsqueda binaria para in devolvería el valor 79[3,5] en la posición 5, o el valor 62[3,3] un lugar antes. Al comparar con 62, y observar que es más pequeño, determinamos que el resultado de búsqueda correcto en es 62[3,3]. El primer "3" en 62[3,3] nos dice que la búsqueda para in debe devolver , un valor de bandera que significa que está más allá del final de la lista . El segundo "3" en 62[3,3] nos dice que la ubicación aproximada de in es la posición 3. Más precisamente, la búsqueda binaria de in devolvería el valor 62[2,3] en la posición 3, o el valor 44[1,2] un lugar antes. Una comparación de con el valor más pequeño 44 nos muestra que el resultado de búsqueda correcto en es 62[2,3]. El "2" en 62[2,3] nos dice que la búsqueda de in debería devolver , y el "3" en 62[2,3] nos dice que el resultado de la búsqueda de in es 79[3,0] en la posición 3 o 46[2,0] en la posición 2; la comparación con 46 muestra que el resultado correcto es 79[3,0] y que el resultado de la búsqueda de in es . Por lo tanto, hemos encontrado en cada una de nuestras cuatro listas, haciendo una búsqueda binaria en la lista única seguida de una comparación única en cada una de las listas sucesivas.
En términos más generales, para cualquier estructura de datos de este tipo, realizamos una consulta haciendo una búsqueda binaria de en y determinando a partir del valor resultante la posición de en . Luego, para cada , usamos la posición conocida de en para encontrar su posición en . El valor asociado con la posición de en apunta a una posición en que es el resultado correcto de la búsqueda binaria de en o está a un solo paso de ese resultado correcto, por lo que pasar de a requiere solo una única comparación. Por lo tanto, el tiempo total para una consulta es
En nuestro ejemplo, las listas en cascada fraccionaria tienen un total de 25 elementos, menos del doble del tamaño de la entrada original. En general, el tamaño de en esta estructura de datos es como máximo , como se puede demostrar fácilmente por inducción. Por lo tanto, el tamaño total de la estructura de datos es como máximo , como se puede ver al reagrupar las contribuciones al tamaño total que provienen de la misma lista de entrada .
En general, la cascada fraccionaria comienza con un gráfico de catálogo , un gráfico dirigido en el que cada vértice está etiquetado con una lista ordenada. Una consulta en esta estructura de datos consta de una ruta en el gráfico y un valor de consulta q ; la estructura de datos debe determinar la posición de q en cada una de las listas ordenadas asociadas con los vértices de la ruta. Para el ejemplo simple anterior, el gráfico de catálogo es en sí mismo una ruta, con solo cuatro nodos. Es posible que los vértices posteriores en la ruta se determinen dinámicamente como parte de una consulta, en respuesta a los resultados encontrados por las búsquedas en partes anteriores de la ruta.
Para manejar consultas de este tipo, para un grafo en el que cada vértice tiene como máximo d aristas entrantes y como máximo d aristas salientes para alguna constante d , las listas asociadas con cada vértice se aumentan con una fracción de los elementos de cada vecino saliente del vértice; la fracción debe elegirse para que sea menor que 1/ d , de modo que la cantidad total por la que se aumentan todas las listas permanezca lineal en el tamaño de entrada. Cada elemento en cada lista aumentada almacena con él la posición de ese elemento en la lista no aumentada almacenada en el mismo vértice, y en cada una de las listas vecinas salientes. En el ejemplo simple anterior, d = 1, y aumentamos cada lista con una fracción de 1/2 de los elementos vecinos.
Una consulta en esta estructura de datos consiste en una búsqueda binaria estándar en la lista aumentada asociada con el primer vértice de la ruta de consulta, junto con búsquedas más simples en cada vértice sucesivo de la ruta. Si se utiliza una fracción de 1/ r de elementos para aumentar las listas a partir de cada elemento vecino, entonces cada resultado sucesivo de la consulta puede encontrarse dentro de un máximo de r pasos de la posición almacenada en el resultado de la consulta del vértice de la ruta anterior y, por lo tanto, puede encontrarse en tiempo constante sin tener que realizar una búsqueda binaria completa.
En la cascada fraccionaria dinámica , la lista almacenada en cada nodo del gráfico del catálogo puede cambiar dinámicamente, mediante una secuencia de actualizaciones en las que se insertan y eliminan elementos de la lista. Esto provoca varias dificultades para la estructura de datos.
En primer lugar, cuando se inserta o se elimina un elemento en un nodo del gráfico del catálogo, debe colocarse dentro de la lista aumentada asociada con ese nodo y puede provocar que los cambios se propaguen a otros nodos del gráfico del catálogo. En lugar de almacenar las listas aumentadas en matrices, se deben almacenar como árboles de búsqueda binaria, de modo que estos cambios se puedan manejar de manera eficiente y al mismo tiempo se puedan realizar búsquedas binarias de las listas aumentadas.
En segundo lugar, una inserción o eliminación puede provocar un cambio en el subconjunto de la lista asociada a un nodo que se pasa a los nodos vecinos del gráfico del catálogo. Ya no es factible, en el entorno dinámico, que este subconjunto se elija como los elementos en cada posición d de la lista, para algún d , ya que este subconjunto cambiaría demasiado drásticamente después de cada actualización. En cambio, una técnica estrechamente relacionada con los árboles B permite la selección de una fracción de datos que se garantiza que sea menor que 1/ d , con los elementos seleccionados espaciados con una cantidad constante de posiciones en la lista completa, y de tal manera que una inserción o eliminación en la lista aumentada asociada a un nodo hace que los cambios se propaguen a otros nodos para una fracción de las operaciones que sea menor que 1/ d . De esta manera, la distribución de los datos entre los nodos satisface las propiedades necesarias para que el algoritmo de consulta sea rápido, al tiempo que garantiza que la cantidad promedio de operaciones de árbol de búsqueda binaria por inserción o eliminación de datos sea constante.
En tercer lugar, y lo más importante, la estructura de datos en cascada fraccionaria estática mantiene, para cada elemento x de la lista aumentada en cada nodo del gráfico del catálogo, el índice del resultado que se obtendría al buscar x entre los elementos de entrada de ese nodo y entre las listas aumentadas almacenadas en los nodos vecinos. Sin embargo, esta información sería demasiado costosa de mantener en la configuración dinámica. Insertar o eliminar un único valor x podría hacer que los índices almacenados en un número ilimitado de otros valores cambiaran. En cambio, las versiones dinámicas de la cascada fraccionaria mantienen varias estructuras de datos para cada nodo:
Estas estructuras de datos permiten realizar una cascada fraccionaria dinámica en un tiempo de O(log n ) por inserción o eliminación, y realizar una secuencia de k búsquedas binarias siguiendo una ruta de longitud k en el gráfico del catálogo en un tiempo O(log n + k log log n ).
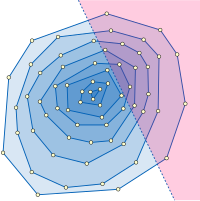
Las aplicaciones típicas de la cascada fraccionaria involucran estructuras de datos de búsqueda de rango en geometría computacional . Por ejemplo, considere el problema del informe de rango de semiplano : es decir, intersecar un conjunto fijo de n puntos con un semiplano de consulta y enumerar todos los puntos en la intersección. El problema es estructurar los puntos de tal manera que una consulta de este tipo pueda responderse de manera eficiente en términos del tamaño de intersección h . Una estructura que se puede utilizar para este propósito son las capas convexas del conjunto de puntos de entrada, una familia de polígonos convexos anidados que consisten en la envoltura convexa del conjunto de puntos y las capas convexas construidas recursivamente de los puntos restantes. Dentro de una sola capa, los puntos dentro del semiplano de consulta pueden encontrarse realizando una búsqueda binaria de la pendiente de la línea límite del semiplano entre la secuencia ordenada de pendientes de aristas de polígonos convexos, que conduce al vértice del polígono que está dentro del semiplano de consulta y más alejado de su límite, y luego buscando secuencialmente a lo largo de las aristas del polígono para encontrar todos los demás vértices dentro del semiplano de consulta. El problema de informe de rango completo del semiplano puede resolverse repitiendo este procedimiento de búsqueda comenzando desde la capa más externa y continuando hacia adentro hasta llegar a una capa que está disjunta del semiespacio de consulta. La cascada fraccionaria acelera las búsquedas binarias sucesivas entre las secuencias de pendientes de aristas de polígonos en cada capa, lo que conduce a una estructura de datos para este problema con espacio O( n ) y tiempo de consulta O(log n + h ). La estructura de datos puede construirse en tiempo O( n log n ) mediante un algoritmo de Chazelle (1985). Como en nuestro ejemplo, esta aplicación implica búsquedas binarias en una secuencia lineal de listas (la secuencia anidada de las capas convexas), por lo que el gráfico del catálogo es solo una ruta.
Otra aplicación de la cascada fraccionaria en las estructuras de datos geométricos se refiere a la ubicación de puntos en una subdivisión monótona, es decir, una partición del plano en polígonos de manera que cualquier línea vertical intersecta cualquier polígono en, como máximo, dos puntos. Como demostraron Edelsbrunner, Guibas y Stolfi (1986), este problema se puede resolver encontrando una secuencia de caminos poligonales que se extiendan de izquierda a derecha a través de la subdivisión y realizando una búsqueda binaria del más bajo de estos caminos que esté por encima del punto de consulta. Probar si el punto de consulta está por encima o por debajo de uno de los caminos se puede resolver como un problema de búsqueda binaria, buscando la coordenada x de los puntos entre las coordenadas x de los vértices del camino para determinar qué borde del camino podría estar por encima o por debajo del punto de consulta. Por lo tanto, cada consulta de ubicación de puntos se puede resolver como una capa externa de búsqueda binaria entre los caminos, cada paso de los cuales realiza a su vez una búsqueda binaria entre las coordenadas x de los vértices. La cascada fraccionaria se puede utilizar para acelerar el tiempo de las búsquedas binarias internas, reduciendo el tiempo total por consulta a O(log n ) utilizando una estructura de datos con espacio O( n ). En esta aplicación, el gráfico del catálogo es un árbol que representa las posibles secuencias de búsqueda de la búsqueda binaria externa.
Más allá de la geometría computacional, Lakshman y Stiliadis (1998) y Buddhikot, Suri y Waldvogel (1999) aplican la cascada fraccional en el diseño de estructuras de datos para el filtrado rápido de paquetes en enrutadores de Internet . Gao et al. (2004) utilizan la cascada fraccional como modelo para la distribución y recuperación de datos en redes de sensores .