En mecánica de suelos , la dilatación o dilatación de corte [1] es el cambio de volumen observado en materiales granulares cuando se someten a deformaciones de corte . [2] [3] Este efecto fue descrito científicamente por primera vez por Osborne Reynolds en 1885/1886 [4] [5] y también se conoce como dilatación de Reynolds . Fue llevado al campo de la ingeniería geotécnica por Peter Walter Rowe [de] . [6]
A diferencia de la mayoría de los demás materiales sólidos, la tendencia de un material granular denso compactado es dilatarse (expandirse en volumen) a medida que se corta. Esto ocurre porque los granos en un estado compactado están entrelazados y, por lo tanto, no tienen la libertad de moverse unos alrededor de otros. Cuando se someten a tensión, se produce un movimiento de palanca entre los granos vecinos, lo que produce una expansión masiva del material. Por otro lado, cuando un material granular comienza en un estado muy suelto, puede compactarse continuamente en lugar de dilatarse bajo el esfuerzo cortante. Una muestra de un material se denomina dilatativa si su volumen aumenta con el aumento del esfuerzo cortante y contractiva si el volumen disminuye con el aumento del esfuerzo cortante. [7] [8]
La dilatación es una característica común de los suelos y las arenas . Su efecto se puede observar cuando la arena húmeda alrededor del pie de una persona que camina por la playa parece secarse. La deformación causada por el pie expande la arena debajo de él y el agua en la arena se mueve para llenar el nuevo espacio entre los granos.
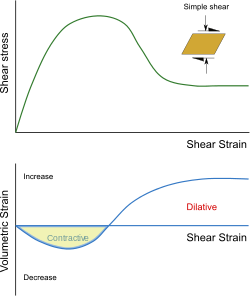
El fenómeno de dilatación se puede observar en un ensayo de corte simple drenado sobre una muestra de arena densa. En la etapa inicial de deformación, la deformación volumétrica disminuye a medida que aumenta la deformación por corte . Pero a medida que la tensión se acerca a su valor máximo, la deformación volumétrica comienza a aumentar. Después de un poco más de corte, la muestra de suelo tiene un volumen mayor que cuando se inició el ensayo.
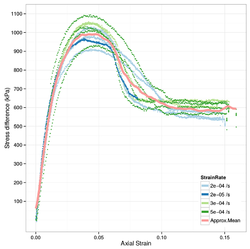
La cantidad de dilatación depende en gran medida de la densidad inicial del suelo. En general, cuanto más denso es el suelo, mayor es la cantidad de expansión de volumen bajo esfuerzo cortante. También se ha observado que el ángulo de fricción interna disminuye a medida que disminuye la tensión normal efectiva . [9]
La relación entre la dilatación y la fricción interna se ilustra típicamente mediante el modelo de dientes de sierra de dilatación, en el que el ángulo de dilatación es análogo al ángulo que forman los dientes con la horizontal. Este modelo se puede utilizar para inferir que el ángulo de fricción observado es igual al ángulo de dilatación más el ángulo de fricción para una dilatación cero. [ cita requerida ]
Debido a la dilatación, el ángulo de fricción aumenta a medida que aumenta el confinamiento hasta alcanzar un valor máximo. Una vez que se moviliza la resistencia máxima del suelo, el ángulo de fricción disminuye abruptamente. Como resultado, la ingeniería geotécnica de taludes, zapatas, túneles y pilotes en dichos suelos debe considerar la posible disminución de la resistencia una vez que la resistencia del suelo alcanza este valor máximo.
El limo mal clasificado o uniformemente con trazas de arena a arenoso que no es plástico puede estar asociado con desafíos durante la construcción, incluso cuando son duros. Estos materiales a menudo parecen ser granulares porque el limo es muy grueso y, por lo tanto, pueden describirse como densos a muy densos. Las excavaciones verticales por debajo del nivel freático en estos tipos de suelo muestran una estabilidad a corto plazo, similar a muchos depósitos de suelo arenoso denso, en parte debido a la succión mátrica. Sin embargo, a medida que se produce el cizallamiento del suelo en la cuña activa debido a las fuerzas de gravedad, se pierde resistencia y se acelera la tasa de falla. Esto puede verse exacerbado por las fuerzas hidrostáticas que se desarrollan en la ubicación o las ubicaciones donde el agua (drena y) se acumula en grietas de tensión en o cerca de la parte posterior de la cuña activa. Generalmente, se manifiesta un desconchado retrógrado, a menudo acompañado de erosión interna o entubada. El uso de filtros apropiados es fundamental para manejar estos materiales; un filtro preferido podría ser una grava clara de tamaño n.° 4 / arena de grano grueso como agregado comercial que generalmente está disponible. Algunas telas de filtro no tejidas también son adecuadas. Como con todos los filtros, se deben comprobar los criterios de compatibilidad D15 y D50.
Después de un intenso esfuerzo cortante, los materiales dilatantes alcanzan un estado de densidad crítica en el que la dilatación ha llegado a su fin. Este fenómeno del comportamiento del suelo se puede incluir en el modelo de suelo endurecido mediante un valor de corte de dilatación. Para especificar este comportamiento, se deben introducir como parámetros generales la relación de vacíos inicial, , y la relación de vacíos máxima, , del material. En cuanto el cambio de volumen da lugar a un estado de vacío máximo, el ángulo de dilatación movilizado, , se vuelve a poner automáticamente a cero. [10]