En mecánica de fracturas , el factor de intensidad de tensión ( K ) se utiliza para predecir el estado de tensión ("intensidad de tensión") cerca de la punta de una grieta o entalla causada por una carga remota o tensiones residuales . [1] Es un constructo teórico que generalmente se aplica a un material elástico lineal homogéneo y es útil para proporcionar un criterio de falla para materiales frágiles , y es una técnica crítica en la disciplina de tolerancia al daño . El concepto también se puede aplicar a materiales que exhiben fluencia a pequeña escala en la punta de una grieta.
La magnitud de K depende de la geometría de la muestra, del tamaño y la ubicación de la grieta o muesca, y de la magnitud y la distribución de las cargas sobre el material. Puede escribirse como: [2] [3]
donde es una función dependiente de la geometría de la muestra de la longitud de la grieta, a , y el ancho de la muestra, W , y σ es la tensión aplicada.
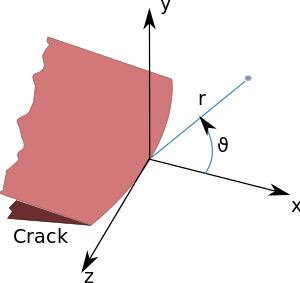
La teoría elástica lineal predice que la distribución de tensión ( ) cerca de la punta de la grieta, en coordenadas polares ( ) con origen en la punta de la grieta, tiene la forma [4]
donde K es el factor de intensidad de tensión (con unidades de tensión × longitud 1/2 ) y es una cantidad adimensional que varía con la carga y la geometría. Teóricamente, cuando r tiende a 0, la tensión tiende a dando como resultado una singularidad de tensión. [5] Sin embargo, en la práctica, esta relación se rompe muy cerca de la punta ( r pequeña ) porque la plasticidad ocurre típicamente en tensiones que exceden la resistencia a la fluencia del material y la solución elástica lineal ya no es aplicable. No obstante, si la zona plástica de la punta de la grieta es pequeña en comparación con la longitud de la grieta, la distribución de tensión asintótica cerca de la punta de la grieta todavía es aplicable.

En 1957, G. Irwin descubrió que las tensiones alrededor de una grieta se podían expresar en términos de un factor de escala llamado factor de intensidad de tensión . Descubrió que una grieta sometida a cualquier carga arbitraria se podía resolver en tres tipos de modos de agrietamiento linealmente independientes. [6] Estos tipos de carga se clasifican como Modo I, II o III como se muestra en la figura. El modo I es un modo de apertura ( tracción ) donde las superficies de la grieta se separan directamente. El modo II es un modo de deslizamiento ( corte en el plano ) donde las superficies de la grieta se deslizan una sobre otra en una dirección perpendicular al borde delantero de la grieta. El modo III es un modo de desgarro ( corte antiplano ) donde las superficies de la grieta se mueven una con respecto a la otra y paralelas al borde delantero de la grieta. El modo I es el tipo de carga más común encontrado en el diseño de ingeniería.
Se utilizan diferentes subíndices para designar el factor de intensidad de tensión para los tres modos diferentes. El factor de intensidad de tensión para el modo I se designa y se aplica al modo de apertura de grietas. El factor de intensidad de tensión del modo II, , se aplica al modo de deslizamiento de grietas y el factor de intensidad de tensión del modo III, , se aplica al modo de desgarro. Estos factores se definen formalmente como: [7]
En condiciones de tensión plana , la tasa de liberación de energía de deformación ( ) para una grieta bajo carga de modo puro I o modo puro II está relacionada con el factor de intensidad de tensión mediante:
donde es el módulo de Young y es el coeficiente de Poisson del material. Se supone que el material es isotrópico, homogéneo y elástico lineal. Se ha supuesto que la grieta se extiende a lo largo de la dirección de la grieta inicial.
Para condiciones de deformación plana , la relación equivalente es un poco más complicada:
Para carga de modo III puro,
donde es el módulo de corte . Para carga general en deformación plana, la combinación lineal es válida:
Se obtiene una relación similar para la tensión plana sumando las contribuciones de los tres modos.
Las relaciones anteriores también se pueden utilizar para conectar la integral J con el factor de intensidad de tensión porque
El factor de intensidad de tensión, , es un parámetro que amplifica la magnitud de la tensión aplicada que incluye el parámetro geométrico (tipo de carga). La intensidad de la tensión en cualquier situación de modo es directamente proporcional a la carga aplicada en el material. Si se puede hacer una grieta muy aguda, o una entalla en V en un material, el valor mínimo de se puede determinar empíricamente, que es el valor crítico de la intensidad de la tensión requerida para propagar la grieta. Este valor crítico determinado para la carga de modo I en deformación plana se conoce como la tenacidad de fractura crítica ( ) del material. tiene unidades de tensión multiplicada por la raíz de una distancia (p. ej. MN/m 3/2 ). Las unidades de implican que la tensión de fractura del material debe alcanzarse en una distancia crítica para que se alcance y se produzca la propagación de la grieta. El factor de intensidad de tensión crítica de modo I, , es el parámetro de diseño de ingeniería utilizado con más frecuencia en la mecánica de fracturas y, por lo tanto, debe comprenderse si vamos a diseñar materiales tolerantes a las fracturas utilizados en puentes, edificios, aviones o incluso campanas.
El pulido no permite detectar una grieta. Normalmente, si se puede ver una grieta, está muy cerca del estado de tensión crítica previsto por el factor de intensidad de tensión [ cita requerida ] .
El criterio G es un criterio de fractura que relaciona el factor de intensidad de tensión crítica (o tenacidad de fractura) con los factores de intensidad de tensión para los tres modos. Este criterio de falla se escribe como [8]
donde es la tenacidad a la fractura, para la deformación plana y para la tensión plana . El factor de intensidad de tensión crítica para la tensión plana se escribe a menudo como .
Si el espaciamiento de grietas es mucho mayor que la longitud de la grieta (h >> a), se puede ignorar el efecto de interacción entre grietas vecinas y el factor de intensidad de tensión es igual al de una sola grieta de longitud 2a.
Entonces el factor de intensidad de tensión en la punta de la grieta es
Si la longitud de la grieta es mucho mayor que el espaciamiento (a >> h ), las grietas pueden considerarse como una pila de grietas semiinfinitas.
Entonces el factor de intensidad de tensión en la punta de la grieta es