Deformación (ingeniería)

Cambio en la forma o tamaño de un objeto

La tensión de compresión produce una deformación que acorta el objeto pero también lo expande hacia afuera.

En ingeniería , la deformación (el cambio de tamaño o forma de un objeto) puede ser elástica o plástica . Si la deformación es despreciable, se dice que el objeto es rígido .

Conceptos principales

La aparición de deformaciones en aplicaciones de ingeniería se basa en los siguientes conceptos básicos:

• Los desplazamientos son cualquier cambio en la posición de un punto sobre el objeto, incluidas las traslaciones y rotaciones de todo el cuerpo ( transformaciones rígidas ).
• Las deformaciones son cambios en la posición relativa entre puntos internos del objeto, excluidas las transformaciones rígidas, que hacen que el cuerpo cambie de forma o tamaño.
• La deformación es ladeformación interna relativa , el cambio adimensional de la forma de un cubo infinitesimal de material en relación con una configuración de referencia. Las deformaciones mecánicas son causadas por la tensión mecánica , véase curva de tensión-deformación .

La relación entre la tensión y la deformación es generalmente lineal y reversible hasta el punto de fluencia y la deformación es elástica . La elasticidad en los materiales se produce cuando la tensión aplicada no supera la energía necesaria para romper los enlaces moleculares, lo que permite que el material se deforme de forma reversible y vuelva a su forma original una vez que se elimina la tensión. La relación lineal para un material se conoce como módulo de Young . Por encima del punto de fluencia, queda cierto grado de distorsión permanente después de la descarga y se denomina deformación plástica . La determinación de la tensión y la deformación en todo un objeto sólido viene dada por el campo de resistencia de los materiales y, para una estructura, por el análisis estructural .

En la figura anterior, se puede ver que la carga de compresión (indicada por la flecha) ha provocado una deformación en el cilindro , de modo que la forma original (líneas discontinuas) ha cambiado (deformado) y ahora tiene los lados abultados. Los lados se abultan porque el material, aunque es lo suficientemente fuerte como para no agrietarse ni fallar de otro modo, no es lo suficientemente fuerte como para soportar la carga sin cambios. Como resultado, el material es expulsado lateralmente. Las fuerzas internas (en este caso en ángulos rectos con respecto a la deformación) resisten la carga aplicada.

Tipos de deformación

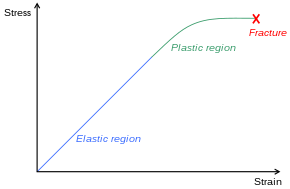
Dependiendo del tipo de material, el tamaño y la geometría del objeto, y las fuerzas aplicadas, pueden producirse distintos tipos de deformación. La imagen de la derecha muestra el diagrama de ingeniería de esfuerzo frente a deformación para un material dúctil típico, como el acero. Pueden producirse distintos modos de deformación en distintas condiciones, como se puede representar mediante un mapa del mecanismo de deformación .

La deformación permanente es irreversible, es decir, la deformación permanece incluso después de retirar las fuerzas aplicadas, mientras que la deformación temporal es recuperable, ya que desaparece después de retirar las fuerzas aplicadas. La deformación temporal también se denomina deformación elástica , mientras que la deformación permanente se denomina deformación plástica .

Diagrama típico de tensión vs. deformación que indica las distintas etapas de deformación.

Deformación elástica

El estudio de la deformación temporal o elástica en el caso de la deformación ingenieril se aplica a materiales utilizados en ingeniería mecánica y estructural, como el hormigón y el acero , que están sometidos a deformaciones muy pequeñas. La deformación ingenieril se modela mediante la teoría de deformaciones infinitesimales , también llamada teoría de deformaciones pequeñas , teoría de deformaciones pequeñas , teoría de desplazamientos pequeños o teoría de gradientes de desplazamientos pequeños, donde tanto las deformaciones como las rotaciones son pequeñas.

Para algunos materiales, por ejemplo, elastómeros y polímeros, sometidos a grandes deformaciones, la definición de ingeniería de deformación no es aplicable, por ejemplo, deformaciones de ingeniería típicas superiores al 1%, ^[1] por lo que se requieren otras definiciones más complejas de deformación, como estiramiento , deformación logarítmica , deformación de Green y deformación de Almansi . Los elastómeros y los metales con memoria de forma, como el Nitinol, presentan amplios rangos de deformación elástica, al igual que el caucho . Sin embargo, la elasticidad no es lineal en estos materiales.

Los metales normales, las cerámicas y la mayoría de los cristales muestran una elasticidad lineal y un rango elástico más pequeño.

La deformación elástica lineal está regida por la ley de Hooke , que establece:

${\displaystyle \sigma =E\varepsilon }$

dónde

• σ es la tensión aplicada ;
• E es una constante material llamada módulo de Young o módulo elástico ;
• ε es la deformación resultante .

Esta relación solo se aplica en el rango elástico e indica que la pendiente de la curva de tensión frente a deformación se puede utilizar para encontrar el módulo de Young ( E ). Los ingenieros suelen utilizar este cálculo en pruebas de tracción. El área bajo esta región elástica se conoce como resiliencia.

Cabe señalar que no todos los materiales elásticos experimentan una deformación elástica lineal; algunos, como el hormigón , la fundición gris y muchos polímeros, responden de manera no lineal. Para estos materiales, la ley de Hooke no es aplicable. ^[2]

Diferencia entre curvas de esfuerzo-deformación verdaderas y de ingeniería

Deformación plástica

Placa de acero de baja aleación y alta resistencia de la marca Swebor, que muestra ambos lados, después de la deformación plástica al detener proyectiles en pruebas balísticas .

Este tipo de deformación no se deshace simplemente eliminando la fuerza aplicada. Sin embargo, un objeto en el rango de deformación plástica habrá sufrido primero una deformación elástica, que se deshace simplemente eliminando la fuerza aplicada, por lo que el objeto volverá parcialmente a su forma original. Los termoplásticos blandos tienen un rango de deformación plástica bastante grande, al igual que los metales dúctiles como el cobre , la plata y el oro . El acero también, pero no el hierro fundido . Los plásticos termoendurecibles duros, el caucho, los cristales y la cerámica tienen rangos de deformación plástica mínimos. Un ejemplo de un material con un rango de deformación plástica grande es la goma de mascar húmeda , que se puede estirar hasta docenas de veces su longitud original.

Bajo tensión de tracción, la deformación plástica se caracteriza por una región de endurecimiento por deformación y una región de estrechamiento y, finalmente, fractura (también llamada ruptura). Durante el endurecimiento por deformación, el material se vuelve más fuerte a través del movimiento de dislocaciones atómicas . La fase de estrechamiento se indica mediante una reducción del área de la sección transversal de la muestra. El estrechamiento comienza después de que se alcanza la resistencia máxima. Durante el estrechamiento, el material ya no puede soportar la tensión máxima y la deformación en la muestra aumenta rápidamente. La deformación plástica termina con la fractura del material.

Diagrama de una curva de tensión-deformación , que muestra la relación entre la tensión (fuerza aplicada) y la deformación (deformación) de un metal dúctil.

Falla

Falla de compresión

Generalmente, la tensión de compresión aplicada a barras, columnas , etc. conduce a un acortamiento.

La carga de un elemento estructural o probeta aumentará la tensión de compresión hasta alcanzar su resistencia a la compresión . Según las propiedades del material, los modos de fallo son de fluencia para materiales con comportamiento dúctil (la mayoría de los metales , algunos suelos y plásticos ) o de ruptura para comportamiento frágil (geomateriales, fundición , vidrio , etc.).

En elementos estructurales largos y delgados, como columnas o armaduras , un aumento de la fuerza de compresión F conduce a una falla estructural debido al pandeo a una tensión menor que la resistencia a la compresión.

Fractura

La rotura se produce cuando el material ha alcanzado el final de su rango de deformación elástica y, luego, plástica. En este punto, las fuerzas se acumulan hasta que son suficientes para provocar una fractura. Todos los materiales acaban por fracturarse si se les aplican fuerzas suficientes.

Tipos de estrés y tensión

La tensión y la deformación de ingeniería son aproximaciones al estado interno que se puede determinar a partir de las fuerzas externas y las deformaciones de un objeto, siempre que no haya un cambio significativo en el tamaño. Cuando hay un cambio significativo en el tamaño, la tensión y la deformación verdaderas se pueden derivar del tamaño instantáneo del objeto.

Estrés y deformación en ingeniería

Consideremos una barra con un área de sección transversal original A ₀ que está sujeta a fuerzas F iguales y opuestas que tiran de los extremos, de modo que la barra está bajo tensión. El material experimenta una tensión definida como la relación entre la fuerza y ​​el área de sección transversal de la barra, así como un alargamiento axial:

El subíndice 0 denota las dimensiones originales de la muestra. La unidad derivada del SI para la tensión es newtons por metro cuadrado, o pascal (1 pascal = 1 Pa = 1 N/m ² ), y la deformación no tiene unidades . La curva de tensión-deformación para este material se traza alargando la muestra y registrando la variación de la tensión con la deformación hasta que la muestra se fractura . Por convención, la deformación se establece en el eje horizontal y la tensión en el eje vertical. Tenga en cuenta que, para fines de ingeniería, a menudo asumimos que el área de la sección transversal del material no cambia durante todo el proceso de deformación. Esto no es cierto, ya que el área real disminuirá mientras se deforma debido a la deformación elástica y plástica. La curva basada en la sección transversal original y la longitud calibrada se denomina curva de tensión-deformación de ingeniería , mientras que la curva basada en el área y la longitud de la sección transversal instantáneas se denomina curva de tensión-deformación verdadera . A menos que se indique lo contrario, generalmente se utiliza la tensión-deformación de ingeniería.

Estrés y tensión verdaderos

La diferencia entre la curva de esfuerzo-deformación real y la curva de esfuerzo-deformación de ingeniería

En las definiciones anteriores de tensión y deformación de ingeniería, se ignoran dos comportamientos de los materiales en ensayos de tracción:

• La reducción del área de la sección
• desarrollo compuesto de elongación

La tensión y la deformación verdaderas se definen de manera diferente a la tensión y la deformación de ingeniería para tener en cuenta estos comportamientos. Se dan como

Aquí las dimensiones son valores instantáneos. Suponiendo que el volumen de la muestra se conserva y la deformación se produce de manera uniforme,

${\displaystyle A_{0}L_{0}=AL}$

La tensión y la deformación verdaderas se pueden expresar mediante la tensión y la deformación de ingeniería. Para la tensión verdadera,

${\displaystyle \sigma _{\mathrm {t} }={\frac {F}{A}}={\frac {F}{A_{0}}}{\frac {A_{0}}{A}}={\frac {F}{A_{0}}}{\frac {L}{L_{0}}}=\sigma (1+\varepsilon )}$

Para la tensión,

${\displaystyle \delta \varepsilon _{\mathrm {t} }={\frac {\delta L}{L}}}$

Integrar ambos lados y aplicar la condición de contorno,

${\displaystyle \varepsilon _{\mathrm {t} }=\ln \left({\frac {L}{L_{0}}}\right)=\ln(1+\varepsilon )}$

Por lo tanto, en una prueba de tensión , la tensión real es mayor que la tensión de ingeniería y la deformación real es menor que la deformación de ingeniería. Por lo tanto, un punto que define la curva tensión-deformación real se desplaza hacia arriba y hacia la izquierda para definir la curva tensión-deformación de ingeniería equivalente. La diferencia entre las tensiones y deformaciones reales y las de ingeniería aumentará con la deformación plástica . A deformaciones bajas (como la deformación elástica ), las diferencias entre las dos son insignificantes. En cuanto al punto de resistencia a la tracción, es el punto máximo en la curva tensión-deformación de ingeniería, pero no es un punto especial en la curva tensión-deformación real. Debido a que la tensión de ingeniería es proporcional a la fuerza aplicada a lo largo de la muestra, el criterio para la formación de estrangulamiento se puede establecer como ${\displaystyle \delta F=0.}$

${\displaystyle {\begin{aligned}&\delta F=\sigma _{\text{t}}\,\delta A+A\,\delta \sigma _{\text{t}}=0\\&-{\frac {\delta A}{A}}={\frac {\delta \sigma _{\mathrm {t} }}{\sigma _{\mathrm {t} }}}\end{aligned}}}$

Este análisis sugiere la naturaleza del punto de resistencia máxima a la tracción (UTS). El efecto de fortalecimiento por trabajo se equilibra exactamente con la contracción del área de la sección en el punto UTS.

Después de la formación del estrechamiento, la muestra sufre una deformación heterogénea, por lo que las ecuaciones anteriores no son válidas. La tensión y la deformación en el estrechamiento se pueden expresar como:

${\displaystyle {\begin{aligned}\sigma _{\mathrm {t} }&={\frac {F}{A_{\mathrm {neck} }}}\\\varepsilon _{\mathrm {t} }&=\ln \left({\frac {A_{0}}{A_{\mathrm {neck} }}}\right)\end{aligned}}}$

Comúnmente se utiliza una ecuación empírica para describir la relación entre la tensión real y la deformación real.

${\displaystyle \sigma _{\mathrm {t} }=K(\varepsilon _{\mathrm {t} })^{n}}$

Aquí, n es el exponente de endurecimiento por deformación y K es el coeficiente de resistencia. n es una medida del comportamiento de endurecimiento por deformación de un material. Los materiales con un valor n más alto tienen una mayor resistencia al estrechamiento. Normalmente, los metales a temperatura ambiente tienen un valor n que varía de 0,02 a 0,5. ^[3]

Discusión

Como no tenemos en cuenta el cambio de área durante la deformación anterior, se debe volver a derivar la curva de tensión y deformación verdadera. Para derivar la curva de tensión y deformación, podemos suponer que el cambio de volumen es cero incluso si deformamos los materiales. Podemos suponer que:

${\displaystyle A_{i}\times \varepsilon _{i}=A_{f}\times \varepsilon _{f}}$

Entonces, el estrés verdadero se puede expresar de la siguiente manera:

${\displaystyle {\begin{aligned}\sigma _{T}={\frac {F}{A_{f}}}&={\frac {F}{A_{i}}}\times {\frac {A_{i}}{A_{f}}}\\&=\sigma _{e}\times {\frac {l_{f}}{l_{i}}}\\[2pt]&=\sigma _{E}\times {\frac {l_{i}+\delta l}{l_{i}}}\\[2pt]&=\sigma _{E}(1+\varepsilon _{E})\end{aligned}}}$

Además, la deformación real ε _T se puede expresar de la siguiente manera:

${\displaystyle \varepsilon _{T}={\frac {dl}{l_{0}}}+{\frac {dl}{l_{1}}}+{\frac {dl}{l_{2}}}+\cdots =\sum _{i}{\frac {dl}{l_{i}}}}$

Luego podemos expresar el valor como

${\displaystyle \int _{l_{0}}^{l_{i}}{\frac {dl}{l}}\,dx=\ln \left({\frac {l_{i}}{l_{0}}}\right)=\ln(1+\varepsilon _{E})}$

De esta manera, podemos inducir la trama en términos de y como figura correcta. ${\displaystyle \sigma _{T}}$ ${\displaystyle \varepsilon _{E}}$

Además, basándonos en la curva de tensión-deformación real, podemos estimar la región donde comienza a producirse el estrechamiento. Dado que el estrechamiento comienza a aparecer después de la tensión de tracción máxima, donde se aplica la fuerza máxima, podemos expresar esta situación de la siguiente manera:

${\displaystyle dF=0=\sigma _{T}dA_{i}+A_{i}d\sigma _{T}}$

Entonces esta forma se puede expresar de la siguiente manera:

${\displaystyle {\frac {d\sigma _{T}}{\sigma _{T}}}=-{\frac {dA_{i}}{A_{i}}}}$

Esto indica que el estrechamiento comienza a aparecer cuando la reducción del área se vuelve mucho más significativa en comparación con el cambio de tensión. Luego, la tensión se localizará en el área específica donde aparece el estrechamiento.

Además, podemos inducir varias relaciones basadas en la verdadera curva de tensión-deformación.

1) La curva de tensión y deformación verdaderas se puede expresar mediante una relación lineal aproximada, tomando el logaritmo de la tensión y deformación verdaderas. La relación se puede expresar de la siguiente manera:

${\displaystyle \sigma _{T}=K\times (\varepsilon _{T})^{n}}$

Donde es el coeficiente de tensión y es el coeficiente de endurecimiento por deformación. Por lo general, el valor de tiene un rango de alrededor de 0,02 a 0,5 a temperatura ambiente. Si es 1, podemos expresar este material como un material elástico perfecto. ^{[4] [5]} ${\displaystyle K}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

2) En realidad, la tensión también depende en gran medida de la tasa de variación de la deformación. Por lo tanto, podemos inducir la ecuación empírica basada en la variación de la tasa de deformación.

${\displaystyle \sigma _{T}=K'\times ({\dot {\varepsilon _{T}}})^{m}}$

Curva de tensión-deformación real del metal FCC y su forma derivada ^[4]

Donde es constante relacionada con la tensión de flujo del material. indica la derivada de la deformación por el tiempo, que también se conoce como velocidad de deformación. es la sensibilidad a la velocidad de deformación. Además, el valor de está relacionado con la resistencia al estrechamiento. Por lo general, el valor de está en el rango de 0-0,1 a temperatura ambiente y tan alto como 0,8 cuando aumenta la temperatura. ${\displaystyle K'}$ ${\displaystyle {\dot {\varepsilon _{T}}}}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$

Combinando 1) y 2), podemos crear la relación definitiva como se muestra a continuación:

${\displaystyle \sigma _{T}=K''\times (\varepsilon _{T})^{n}({\dot {\varepsilon _{T}}})^{m}}$

¿Dónde está la constante global para relacionar la deformación, la velocidad de deformación y el estrés? ${\displaystyle K''}$

3) Con base en la curva de esfuerzo-deformación real y su forma derivada, podemos estimar la deformación necesaria para iniciar el estrechamiento. Esto se puede calcular con base en la intersección entre la curva de esfuerzo-deformación real, como se muestra a la derecha.

Esta figura también muestra la dependencia de la deformación por estrangulamiento a diferentes temperaturas. En el caso de los metales FCC, ambas curvas de tensión-deformación en su derivada dependen en gran medida de la temperatura. Por lo tanto, a mayor temperatura, el estrangulamiento comienza a aparecer incluso con valores de deformación más bajos.

Todas estas propiedades indican la importancia de calcular la verdadera curva de tensión-deformación para analizar más a fondo el comportamiento de los materiales en entornos repentinos.

4) Un método gráfico, denominado "construcción de consideración", puede ayudar a determinar el comportamiento de la curva de tensión-deformación, ya sea que se produzca estrangulamiento o estiramiento en la muestra. Al establecer como determinante, la tensión y la deformación reales se pueden expresar con la tensión y la deformación de ingeniería como se muestra a continuación: ${\displaystyle \lambda =L/L_{0}}$

${\displaystyle \sigma _{T}=\sigma _{e}\times \lambda ,\qquad \varepsilon _{T}=\ln \lambda .}$

Por lo tanto, el valor de la tensión de ingeniería se puede expresar mediante la línea secante que se obtiene a partir de la tensión real y el valor donde . Al analizar la forma del diagrama y la línea secante, podemos determinar si los materiales presentan estiramiento o estrangulamiento. ${\displaystyle \lambda }$ ${\displaystyle \lambda =0}$ ${\displaystyle \lambda =1}$ ${\displaystyle \sigma _{T}-\lambda }$

Consideremos la gráfica. (a) Curva tensión-deformación verdadera sin tangentes. No hay estrangulamiento ni estiramiento. (b) Con una tangente. Solo hay estrangulamiento. (c) Con dos tangentes. Hay estrangulamiento y estiramiento. ^[6]

En la figura (a), solo hay una gráfica cóncava hacia arriba. Esto indica que no hay una caída en el rendimiento, por lo que el material sufrirá una fractura antes de ceder. En la figura (b), hay un punto específico donde la tangente coincide con la línea secante en el punto donde . Después de este valor, la pendiente se vuelve más pequeña que la línea secante donde comienza a aparecer el estrechamiento. En la figura (c), hay un punto donde comienza a aparecer el rendimiento, pero cuando , se produce el estiramiento. Después del estiramiento, todo el material se estirará y eventualmente mostrará una fractura. Entre y , el material en sí no se estira, sino que solo el cuello comienza a estirarse. ${\displaystyle \lambda =\lambda _{Y}}$ ${\displaystyle \lambda =\lambda _{d}}$ ${\displaystyle \lambda _{Y}}$ ${\displaystyle \lambda _{d}}$

Conceptos erróneos

Un error muy extendido es creer que todos los materiales que se doblan son "débiles" y los que no lo hacen son "fuertes". En realidad, muchos materiales que sufren grandes deformaciones elásticas y plásticas, como el acero, son capaces de absorber tensiones que harían que se rompieran materiales frágiles, como el vidrio, con rangos mínimos de deformación plástica. ^[7]

Véase también

• Deformación craneal artificial
• Fuerza de potenciación
• Fluencia (deformación)
• Deflexión (ingeniería)
• Deformación (mecánica)
• Mapas de mecanismos de deformación
• Monitoreo de deformaciones
• Retracción de deformación
• Teoría de la deformación
• Elasticidad
• Maleabilidad
• Características de deformación plana
• Plasticidad (física)
• Coeficiente de Poisson
• Tensor de deformación
• Resistencia de los materiales
• Deformación de la madera

Referencias

1. Rees, David (2006). Plasticidad básica en ingeniería: una introducción con aplicaciones en ingeniería y fabricación. Butterworth-Heinemann. pág. 41. ISBN 0-7506-8025-3Archivado desde el original el 22 de diciembre de 2017.
2. Callister, William D. (2004) Fundamentos de la ciencia y la ingeniería de los materiales , John Wiley and Sons, 2.ª ed., pág. 184. ISBN 0-471-66081-7 . 
3. Courtney, Thomas (2005). Comportamiento mecánico de los materiales . Waveland Press, Inc., págs. 6-13.
4. Courtney, Thomas (2000). Comportamiento mecánico de los materiales . Illinois: Waveland Press. pág. 165. ISBN 9780073228242.
5. "Estrés y tensión verdaderos" (PDF) . Archivado desde el original (PDF) el 27 de enero de 2018 . Consultado el 15 de mayo de 2018 .
6. Roland, David. «CURVAS DE TENSIÓN-DEFORMACIÓN» (PDF) . MIT .
7. Rice, Peter y Dutton, Hugh (1995). Vidrio estructural. Taylor & Francis. pág. 33. ISBN 0-419-19940-3.{{cite book}}: CS1 maint: multiple names: authors list (link)