Triangulación (topología)

Un toro triangular

Otra triangulación del toro

Una forma de delfín triangulada.

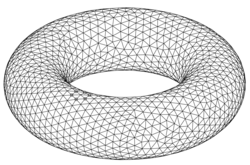
En matemáticas, la triangulación describe la sustitución de espacios topológicos por espacios lineales por partes , es decir, la elección de un homeomorfismo en un complejo simplicial adecuado . Los espacios que son homeomorfos a un complejo simplicial se denominan triangulares. La triangulación tiene varios usos en diferentes ramas de las matemáticas, por ejemplo en topología algebraica, en análisis complejos o en modelado.

Motivación

Por un lado, a veces resulta útil olvidarse de la información superflua de los espacios topológicos: la sustitución de los espacios originales por complejos simpliciales puede ayudar a reconocer propiedades cruciales y a obtener una mejor comprensión del objeto considerado.

Por otro lado, los complejos simpliciales son objetos de carácter combinatorio y por lo tanto se les pueden asignar cantidades que surgen de su patrón combinatorio, por ejemplo, la característica de Euler . La triangulación permite ahora asignar tales cantidades a espacios topológicos.

Las investigaciones sobre la existencia y unicidad de las triangulaciones establecieron una nueva rama de la topología: la topología lineal por partes (topología PL corta). Su objetivo principal son las propiedades topológicas de los complejos simpliciales y su generalización, los complejos celulares.

Complejos simples

Complejos simpliciales abstractos

Un complejo simplicial abstracto sobre un conjunto es un sistema de subconjuntos no vacíos tal que: ${\displaystyle V}$ ${\displaystyle {\mathcal {T}}\subset {\mathcal {P}}(V)}$

• ${\displaystyle \{v_{0}\}\in {\mathcal {T}}}$para cada ; ${\displaystyle v_{0}\in V}$
• si y . ${\displaystyle E\in {\mathcal {T}}}$ ${\displaystyle \emptyset \neq F\subset E}$ ${\displaystyle \Rightarrow }$ ${\displaystyle F\in {\mathcal {T}}}$

Los elementos de se llaman simples, los elementos de se llaman vértices. Un simplex con vértices tiene dimensión por definición. La dimensión de un complejo simplicial abstracto se define como . ^[1] ${\displaystyle {\mathcal {T}}}$ ${\displaystyle V}$ ${\displaystyle n+1}$ ${\displaystyle n}$ ${\displaystyle {\text{dim}}({\mathcal {T}})={\text{sup}}\;\{{\text{dim}}(F):F\in {\mathcal {T}}\}\in \mathbb {N} \cup \infty }$

Los complejos abstractos simpliciales también pueden considerarse objetos geométricos. Esto requiere el término de simplex geométrico.

Simplicidades geométricas en dimensión 1, 2 y 3.

Simplicidades geométricas

Sean puntos afínmente independientes en , es decir, los vectores son linealmente independientes . Se dice que el conjunto es el simplex abarcado por . Tiene dimensión por definición. Los puntos se llaman vértices de , los símplices abarcados por de los vértices se llaman caras y el límite se define como la unión de sus caras. ${\displaystyle p_{0},...p_{n}}$ ${\displaystyle n+1}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle (p_{1}-p_{0}),(p_{2}-p_{0}),\dots (p_{n}-p_{0})}$ ${\textstyle \Delta ={\Bigl \{}x\in \mathbb {R} ^{n}\;{\Big |}\;x=\sum _{i=0}^{n}t_{i}p_{i}\;with\;0\leq t_{i}\leq 1\;and\;\sum _{i=0}^{n}t_{i}=1{\Bigr \}}}$ ${\displaystyle p_{0},...p_{n}}$ ${\displaystyle n}$ ${\displaystyle p_{0},...p_{n}}$ ${\displaystyle \Delta }$ ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle \partial \Delta }$

El símplex estándar dimensional es el símplex abarcado por los vectores unitarios ^[2] ${\displaystyle n}$ ${\displaystyle e_{0},...e_{n}}$

Complejos geométricos simpliciales

Un complejo geométrico simplicial es una unión de simples geométricos tales que ${\displaystyle {\mathcal {S}}\subset \mathbb {R} ^{n}}$

• Si es un simplex en , entonces todas sus caras están en . ${\displaystyle S}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}}$
• Si hay dos simples distintos en , sus interiores son disjuntos. ${\displaystyle S,T}$ ${\displaystyle {\mathcal {S}}}$

El conjunto se puede realizar como un espacio topológico eligiendo los conjuntos cerrados para que sean cerrados para todos . Cabe mencionar que, en general, el complejo simplicial no proporcionará la topología natural de . En el caso de que cada punto del complejo se encuentre sólo en un número fino de símplices, ambas topologías coinciden ^[2] ${\displaystyle {\mathcal {S}}}$ ${\displaystyle |{\mathcal {S}}|}$ ${\displaystyle {\Bigl \{}A\subset |{\mathcal {S}}|\;{\Big |}\;A\cap \Delta }$ ${\displaystyle \Delta \in {\mathcal {S}}{\Bigr \}}}$ ${\displaystyle \mathbb {R} ^{n}}$

Cada complejo geométrico puede asociarse a un complejo abstracto eligiendo como conjunto fundamental el conjunto de vértices que aparecen en cualquier símplex de y como sistema de subconjuntos cuyos subconjuntos corresponden a conjuntos de vértices de símplices en . ${\displaystyle V}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {S}}}$

Una pregunta natural es si, a la inversa, cualquier complejo simplicial abstracto corresponde a un complejo geométrico. En general, la construcción geométrica como se menciona aquí no es lo suficientemente flexible: considere, por ejemplo, un complejo simple abstracto de dimensión infinita. Sin embargo, la siguiente construcción más abstracta proporciona un espacio topológico para cualquier tipo de complejo simplicial abstracto:

Sea un complejo simplicial abstracto sobre un conjunto . Elija una unión de simples , pero cada uno de dimensión suficientemente grande, de modo que el simplex geométrico sea de dimensión si el simplex geométrico abstracto tiene dimensión . Si , se puede identificar con una cara de y el espacio topológico resultante es el encolado. Efectuando el encolado para cada inclusión, se termina con el espacio topológico deseado. ${\displaystyle {\mathcal {T}}}$ ${\displaystyle V}$ ${\displaystyle (\Delta _{F})_{F\in {\mathcal {T}}}}$ ${\displaystyle \mathbb {R} ^{N}}$ ${\displaystyle \Delta _{F}}$ ${\displaystyle n}$ ${\displaystyle F}$ ${\displaystyle n}$ ${\displaystyle E\subset F}$ ${\displaystyle \Delta _{E}\subset \mathbb {R} ^{N}}$ ${\displaystyle \Delta _{F}\subset \mathbb {R} ^{M}}$ ${\displaystyle \Delta _{E}\cup _{i}\Delta _{F}}$

Un complejo simplicial geométrico bidimensional con vértice V, enlace (V) y estrella (V) están resaltados en rojo y rosa.

Como en la construcción anterior, por la topología inducida por pegado, los conjuntos cerrados en este espacio son los subconjuntos que se cierran en la topología subespacial de cada simplex . ${\displaystyle \Delta _{F}}$

El complejo simplicial , que consta de todos los símplices de dimensión , se denomina esqueleto -ésimo de . ${\displaystyle {\mathcal {T_{n}}}}$ ${\displaystyle {\mathcal {T}}}$ ${\displaystyle \leq n}$ ${\displaystyle n}$ ${\displaystyle {\mathcal {T}}}$

Una vecindad natural de un vértice de un complejo simplicial se considera la estrella de un simplex, su límite es el enlace ${\displaystyle V}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle star(K)={\Big \{}L\in {\mathcal {S}}\;|\;K\subset L{\Big \}}}$

${\displaystyle lk(K)={\Big \{}M\in {\mathcal {S}}\;|\;M\cap K=\emptyset {\Big \}}}$.

Mapas simples

Los mapas considerados en esta categoría son mapas simpliciales: Sean , complejos simpliciales abstractos sobre conjuntos , . Un mapa simplicial es una función que asigna cada simplex a un simplex . Por extensión lineal afín sobre los simples, induce un mapa entre las realizaciones geométricas de los complejos. ^[2] ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle V_{K}}$ ${\displaystyle V_{L}}$ ${\displaystyle f:V_{K}\rightarrow V_{L}}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle f}$

Ejemplos

• Deja y deja . El complejo geométrico asociado es una estrella con centro . ${\displaystyle W=\{a,b,c,d,e,f\}}$ ${\displaystyle {\mathcal {T}}={\Big \{}\{a\},\{b\},\{c\},\{d\},\{e\},\{f\},\{a,b\},\{a,c\},\{a,d\},\{a,e\},\{a,f\}{\Big \}}}$ ${\displaystyle \{a\}}$
• Deja y deja . Su realización geométrica es un tetraedro . ${\displaystyle V=\{A,B,C,D\}}$ ${\displaystyle {\mathcal {S}}={\mathcal {P}}(V)}$ ${\displaystyle |{\mathcal {S}}|}$
• Dejemos como arriba y dejemos . El complejo geométrico simplicial es la frontera de un tetraedro . ${\displaystyle V}$ ${\displaystyle {\mathcal {S}}'=\;{\mathcal {P}}({\mathcal {V}})\setminus \{A,B,C,D\}}$ ${\displaystyle |{\mathcal {S'}}|=\partial |{\mathcal {S}}|}$

Definición

Una triangulación de un espacio topológico es un homeomorfismo donde hay un complejo simplicial. Los espacios topológicos no necesariamente admiten una triangulación y si la admiten no necesariamente son únicas. ${\displaystyle X}$ ${\displaystyle t:|{\mathcal {T}}|\rightarrow X}$ ${\displaystyle {\mathcal {T}}}$

Ejemplos

• Los complejos simples se pueden triangular por identidad.
• Sea como en los ejemplos vistos arriba. La bola unitaria cerrada es homeomorfa a un tetraedro por lo que admite una triangulación, concretamente el homeomorfismo . Restringir a produce un homeomorfismo . ${\displaystyle {\mathcal {S}},{\mathcal {S'}}}$ ${\displaystyle \mathbb {D} ^{3}}$ ${\displaystyle t:|{\mathcal {S}}|\rightarrow \mathbb {D} ^{3}}$ ${\displaystyle t}$ ${\displaystyle |{\mathcal {S}}'|}$ ${\displaystyle t':|{\mathcal {S}}'|\rightarrow \mathbb {S} ^{2}}$

La esfera bidimensional y una triangulación.

• El toro admite una triangulación. Para ver esto, considere el toroide como un cuadrado donde las caras paralelas están pegadas. Este cuadrado se puede triangular como se muestra a continuación: ${\displaystyle \mathbb {T} ^{2}=\mathbb {S} ^{1}\times \mathbb {S} ^{1}}$

Un toro bidimensional, representado como el pegado de un cuadrado mediante el mapa g, identificando sus sitios opuestos

• El plano proyectivo admite una triangulación (ver complejos CW) ${\displaystyle \mathbb {P} ^{2}}$
• Se puede demostrar que las variedades diferenciables admiten triangulaciones. ^[3]

Invariantes

Las triangulaciones de espacios permiten asignar invariantes combinatorios que surgen de sus complejos simpliciales dedicados a los espacios. Estas son características iguales para complejos que son isomórficos a través de un mapa simplicial y, por lo tanto, tienen el mismo patrón combinatorio.

Estos datos podrían ser útiles para clasificar espacios topológicos hasta el homeomorfismo, pero sólo dado que las características también son invariantes topológicas, es decir, no dependen de la triangulación elegida. Para los datos enumerados aquí, este es el caso. ^[4] Para obtener detalles y el vínculo con la homología singular , consulte invariancia topológica.

Homología

Mediante triangulación, se puede asignar un complejo de cadena a espacios topológicos que surgen de su complejo simplicial y calcular su homología simplicial . Los espacios compactos siempre admiten triangulaciones finitas y, por tanto, sus grupos de homología se generan de forma finita y sólo un número finito de ellos no desaparecen. Otros datos como los números de Betti o las características de Euler pueden derivarse de la homología.

Betti- números y características de Euler

Sea un complejo simplicial finito. El -ésimo número de Betti- se define como el rango del -ésimo grupo de homología simplicial de los espacios. Estos números codifican propiedades geométricas de los espacios: el número Betti, por ejemplo, representa el número de componentes conectados . Para superficies orientables cerradas y trianguladas , se cumple donde denota el género de la superficie: por lo tanto, su primer número de Betti representa el número duplicado de asas de la superficie. ^[5] ${\displaystyle |{\mathcal {S}}|}$ ${\displaystyle n}$ ${\displaystyle b_{n}({\mathcal {S}})}$ ${\displaystyle n}$ ${\displaystyle b_{0}({\mathcal {S}})}$ ${\displaystyle F}$ ${\displaystyle b_{1}(F)=2g}$ ${\displaystyle g}$

Con los comentarios anteriores, para espacios compactos todos los números de Betti son finitos y casi todos son cero. Por lo tanto, se puede formar su suma alterna.

${\displaystyle \sum _{k=0}^{\infty }(-1)^{k}b_{k}({\mathcal {L}})}$

que se llama Euler Charakteristik del complejo, una invariante topológica pegadiza.

Invariancia topológica

Para utilizar estos invariantes para la clasificación de espacios topológicos hasta el homeomorfismo se necesita la invariancia de las características con respecto al homeomorfismo.

Un enfoque famoso a la cuestión fue a principios del siglo XX el intento de demostrar que dos triangulaciones cualesquiera del mismo espacio topológico admiten una subdivisión común . Esta suposición se conoce como Hauptvermutung ( en alemán: Suposición principal). Sea un complejo simple. Se dice que un complejo es una subdivisión de si: ${\displaystyle |{\mathcal {L}}|\subset \mathbb {R} ^{N}}$ ${\displaystyle |{\mathcal {L'}}|\subset \mathbb {R} ^{N}}$ ${\displaystyle {\mathcal {L}}}$

• todo simplex de está contenido en un simplex de y ${\displaystyle {\mathcal {L'}}}$ ${\displaystyle {\mathcal {L}}}$
• cada simplex de es una unión finita de simples en . ^[2] ${\displaystyle {\mathcal {L}}}$ ${\displaystyle {\mathcal {L'}}}$

Esas condiciones aseguran que las subdivisiones no cambien el complejo simplicial como conjunto o como espacio topológico. Se dice que una aplicación entre complejos simpliciales es lineal por partes si hay un refinamiento de tal que sea lineal por partes en cada simplex de . Se dice que dos complejos que se corresponden entre sí mediante biyección lineal por partes son isomórficos combinatorios. En particular, dos complejos que tienen un refinamiento común son combinatoriamente equivalentes. Los grupos de homología son invariantes a la equivalencia combinatoria y, por tanto, la Hauptvermutung daría la invariancia topológica de los grupos de homología simpliciales. En 1918, Alejandro introdujo el concepto de homología singular. De ahora en adelante, la mayoría de las invariantes que surgen de la triangulación fueron reemplazadas por invariantes que surgen de la homología singular. Para esos nuevos invariantes, se puede demostrar que eran invariantes con respecto al homeomorfismo e incluso con respecto a la equivalencia de homotopía. ^[6] Además, se demostró que los grupos de homología singular y simplicial coinciden. ^[6] Esta solución ha demostrado la invariancia de los datos al homeomorfismo. La Hauptvermutung perdió importancia, pero fue la inicial para una nueva rama de la topología: la topología lineal por partes (topología PL corta) examina las propiedades topológicas de los espacios topológicos. ^[7] ${\displaystyle f:{\mathcal {K}}\rightarrow {\mathcal {L}}}$ ${\displaystyle {\mathcal {K'}}}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle f}$ ${\displaystyle {\mathcal {K}}}$

Hauptvermutung

La Hauptvermutung ( conjetura principal en alemán ) afirma que dos triangulaciones siempre admiten una subdivisión común. Originalmente, su propósito era demostrar la invariancia de invariantes combinatorios con respecto a los homeomorfismos. La suposición de que tales subdivisiones existen en general es intuitiva, ya que las subdivisiones son fáciles de construir para espacios simples, por ejemplo, para variedades de baja dimensión. De hecho, la suposición fue probada para variedades de dimensión y para variedades diferenciables, pero fue refutada en general: ^[8] Una herramienta importante para mostrar que las triangulaciones no admiten una subdivisión común. i. Si sus complejos subyacentes no son combinatoriamente isomórficos es el invariante combinatorio de Reidemeister Torsion. ${\displaystyle \leq 3}$

Torsión de Reidemeister

Para refutar la Hauptvermutung es útil utilizar invariantes combinatorios que no sean invariantes topológicos. Un ejemplo famoso es Reidemeister-Torsion. Se puede asignar a una tupla de complejos CW-: Si esta característica será una invariante topológica pero si en general no. Una aproximación a la Hauptvermutung fue encontrar espacios homeomórficos con diferentes valores de Reidemeister-Torsion. Esta invariante se utilizó inicialmente para clasificar espacios de lentes y los primeros contraejemplos de la Hauptvermutung se construyeron basándose en espacios de lentes: ^[8] ${\displaystyle (K,L)}$ ${\displaystyle L=\emptyset }$ ${\displaystyle L\neq \emptyset }$

Clasificación de espacios lenticulares.

En su formulación original, los espacios de Lens son 3 variedades, construidos como espacios cocientes de 3 esferas: Sean números naturales, tales que sean coprimos. El espacio de la lente se define como el espacio de órbita de la acción del grupo libre. ${\displaystyle p,q}$ ${\displaystyle p,q}$ ${\displaystyle L(p,q)}$

${\displaystyle \mathbb {Z} /p\mathbb {Z} \times S^{3}\to S^{3}}$

${\displaystyle (k,(z_{1},z_{2}))\mapsto (z_{1}\cdot e^{2\pi ik/p},z_{2}\cdot e^{2\pi ikq/p})}$.

Para diferentes tuplas , los espacios de Lens serán homotópicos equivalentes pero no homeomórficos. Por lo tanto, no se pueden distinguir con la ayuda de invariantes clásicas como grupo fundamental sino mediante el uso de Reidemeister-Torsion. ${\displaystyle (p,q)}$

Dos espacios de Lens son homeomorfos, si y sólo si . ^[9] Este es el caso si dos espacios de lentes son equivalentes a homotopía simple . Este hecho puede utilizarse para construir contraejemplos para la Hauptvermutung de la siguiente manera. Supongamos que hay espacios derivados de espacios de lentes no homeomórficos que tienen diferente torsión de Reidemeister. Supongamos además que la modificación en no afecta la torsión de Reidemeister pero que después de la modificación y son homeomorfas. Los espacios resultantes desmentirán la Hauptvermutung. ${\displaystyle L(p,q_{1}),L(p,q_{2})}$ ${\displaystyle q_{1}\equiv \pm q_{2}^{\pm 1}{\pmod {p}}}$ ${\displaystyle L'_{1},L'_{2}}$ ${\displaystyle L(p,q_{1}),L(p,q_{2})}$ ${\displaystyle L'_{1},L'_{2}}$ ${\displaystyle L'_{1}}$ ${\displaystyle L'_{2}}$

Existencia de triangulación

Además de la cuestión de triangulaciones concretas para cuestiones computacionales, hay afirmaciones sobre espacios que son más fáciles de demostrar dado que son complejos simpliciales. Especialmente interesantes son las variedades. Las variedades topológicas de dimensión siempre son triangulares ^{[10] [11] [1]} pero hay variedades no triangulares para dimensión , arbitrarias pero mayores que tres. ^{[12] [13]} Además, las variedades diferenciables siempre admiten triangulaciones. ^[3] ${\displaystyle \leq 3}$ ${\displaystyle n}$ ${\displaystyle n}$

PL- Estructuras

Los colectores son una clase importante de espacios. Es natural exigir que no sólo sean triangulares sino que además admitan un atlas lineal por partes, una estructura PL:

Sea un complejo simplicial tal que cada punto admita una vecindad abierta tal que haya una triangulación y un homeomorfismo lineal por partes . Entonces se dice que es una variedad de dimensión lineal por partes (PL) y la triangulación junto con el atlas PL se dice que es una estructura PL en . ${\displaystyle |X|}$ ${\displaystyle U}$ ${\displaystyle U}$ ${\displaystyle f:U\rightarrow \mathbb {R} ^{n}}$ ${\displaystyle |X|}$ ${\displaystyle n}$ ${\displaystyle |X|}$

Un lema importante es el siguiente:

Sea un espacio topológico. es equivalente ${\displaystyle X}$

1. ${\displaystyle X}$es una variedad -dimensional y admite una estructura PL-. ${\displaystyle n}$
2. Existe una triangulación tal que el vínculo de cada vértice es una esfera. ${\displaystyle X}$ ${\displaystyle n-1}$
3. Por cada triangulación del eslabón de cada vértice es una esfera. ${\displaystyle X}$ ${\displaystyle n-1}$

La equivalencia del segundo y tercer enunciado se debe a que el vínculo de un vértice es independiente de la triangulación elegida hasta el isomorfismo combinatorio. ^[14] Se puede demostrar que las variedades diferenciables admiten una estructura PL, así como variedades de dimensión . ^[15] Los contraejemplos para la conjetura de triangulación son contraejemplos para la conjetura de la existencia de una estructura PL, por supuesto. ${\displaystyle \leq 3}$

Además, hay ejemplos de espacios triangulados que no admiten una estructura PL. Considere una esfera de homología PL dimensional . La doble suspensión es una esfera topológica. Al elegir una triangulación obtenida mediante la operación de suspensión de triangulaciones, el complejo simplicial resultante no es una variedad PL, porque hay un vértice tal que no es una esfera. ^[dieciséis] ${\displaystyle n-2}$ ${\displaystyle X}$ ${\displaystyle S^{2}X}$ ${\displaystyle n}$ ${\displaystyle t:|{\mathcal {S}}|\rightarrow S^{2}X}$ ${\displaystyle v}$ ${\displaystyle link(v)}$ ${\displaystyle n-1}$

Una pregunta que surge con la definición es si las estructuras PL son siempre únicas: dadas dos estructuras PL para el mismo espacio , ¿existe un homeomorfismo que sea lineal por partes con respecto a ambas estructuras PL? La suposición es similar a la Hauptvermutung y, de hecho, hay espacios que tienen diferentes estructuras PL que no son equivalentes. La triangulación de espacios equivalentes a PL se puede transformar entre sí mediante movimientos de Pachner: ${\displaystyle Y}$ ${\displaystyle F:Y\rightarrow Y}$

Movimientos de Pachner

Un movimiento de Pachner reemplaza dos tetraedros por tres tetraedros

Los movimientos de Pachner son una forma de manipular triangulaciones: sea un complejo simple. Para dos simples la unión ${\displaystyle {\mathcal {S}}}$ ${\displaystyle K,L}$

${\displaystyle K*L={\Big \{}tk+(1-t)l\;|\;k\in K,l\in L\;t\in [0,1]{\Big \}}}$son los puntos que se encuentran en rectas entre los puntos en y en . Elija tal que para cualquier mentira no en . Se puede obtener un nuevo complejo reemplazando por . Este reemplazo se llama movimiento de Pachner. El teorema de Pachner establece que siempre que dos variedades trianguladas son equivalentes a PL, hay una serie de movimientos de Pachner que transforman ambas en otras. ^[17] ${\displaystyle K}$ ${\displaystyle L}$ ${\displaystyle S\in {\mathcal {S}}}$ ${\displaystyle lk(S)=\partial K}$ ${\displaystyle K}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S'}}}$ ${\displaystyle S*\partial K}$ ${\displaystyle \partial S*K}$

complejos CW

El plano proyectivo real como complejo simplicial y como complejo CW-. Como complejo CW, se puede obtener pegando primero y obteniendo la 1 esfera y luego uniendo el disco por el mapa . ${\displaystyle \mathbb {D} ^{0}}$ ${\displaystyle \mathbb {D} ^{1}}$ ${\displaystyle \mathbb {D} ^{2}}$ ${\displaystyle g:\mathbb {S} ^{1}\rightarrow \mathbb {S} ^{1},e^{ix}\mapsto e^{2ix}}$

Una construcción similar pero más flexible que los complejos simpliciales es la de los complejos CW. Su construcción es la siguiente:

Una celda es la bola unitaria de dimensión cerrada , una celda abierta es su interior . Sea un espacio topológico, sea un mapa continuo. Se dice que el pegado se obtiene pegando una celda. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle B_{n}=[0,1]^{n}}$ ${\displaystyle n}$ ${\displaystyle B_{n}=[0,1]^{n}\setminus \mathbb {S} ^{n-1}}$ ${\displaystyle X}$ ${\displaystyle f:\mathbb {S} ^{n-1}\rightarrow X}$ ${\displaystyle X\cup _{f}B_{n}}$ ${\displaystyle n}$

Un complejo celular es una unión de espacios topológicos tales que ${\displaystyle X=\cup _{n\geq 0}X_{n}}$

• ${\displaystyle X_{0}}$es un conjunto discreto
• cada uno se obtiene pegando una familia de células. ${\displaystyle X_{n}}$ ${\displaystyle X_{n-1}}$ ${\displaystyle n}$

Cada complejo simplicial es un complejo CW; lo inverso no es cierto. La construcción de complejos CW- se puede utilizar para definir la homología celular y se puede demostrar que la homología celular y la homología simplicial coinciden. ^[18] Para cuestiones computacionales, a veces es más fácil asumir que los espacios son complejos CW y determinar su homología mediante descomposición celular; un ejemplo es el plano proyectivo : su construcción como complejo CW necesita tres celdas, mientras que su complejo simplicial consta de 54 simples. ${\displaystyle \mathbb {P} ^{2}}$

Otras aplicaciones

Clasificación de colectores.

Al triangular variedades unidimensionales, se puede demostrar que siempre son homeomorfas para separar copias de la línea real y la esfera unitaria . Además, las superficies, es decir, 2 variedades, se pueden clasificar completamente: Sea una superficie compacta. ${\displaystyle \mathbb {S} ^{1}}$ ${\displaystyle S}$

• Si es orientable, es homeomorfo a una 2 esferas con toros de dimensión adjuntos, para algunos . ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle 2}$ ${\displaystyle n\geq 0}$
• Si no es orientable, para algunos es homeomorfo a una botella de Klein con toros de dimensión adjuntos . ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle 2}$ ${\displaystyle n\geq 0}$

Para demostrar este teorema se construye un polígono fundamental de la superficie: esto se puede hacer utilizando la estructura simple obtenida por la triangulación. ^[19]

Mapas sobre complejos simpliciales.

Dar a los espacios la estructura de una estructura simple podría ayudar a comprender los mapas definidos en los espacios. A menudo se puede suponer que los mapas son mapas simpliciales mediante el teorema de aproximación simplicial:

Aproximación simple

Sean , complejos simpliciales abstractos sobre conjuntos , . Un mapa simplicial es una función que asigna cada simplex a un simplex . Por extensión lineal afín sobre los simples, induce un mapa entre las realizaciones geométricas de los complejos. Cada punto de un complejo geométrico se encuentra en el interior de exactamente un simplex, su soporte. Consideremos ahora un mapa continuo . Se dice que una aplicación simplicial es una aproximación simple de si y sólo si cada uno de ellos se asigna sobre el soporte de in . Si tal aproximación existe, se puede construir una homotopía transformándose en definiéndola en cada simplex; ahí siempre existe, porque los simples son contráctiles. ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle V_{K}}$ ${\displaystyle V_{L}}$ ${\displaystyle f:V_{K}\rightarrow V_{L}}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle f}$ ${\displaystyle f:{\mathcal {K}}\rightarrow {\mathcal {L}}}$ ${\displaystyle g:{\mathcal {K}}\rightarrow {\mathcal {L}}}$ ${\displaystyle f}$ ${\displaystyle x\in {\mathcal {K}}}$ ${\displaystyle g}$ ${\displaystyle f(x)}$ ${\displaystyle {\mathcal {L}}}$ ${\displaystyle H}$ ${\displaystyle f}$ ${\displaystyle g}$

El teorema de aproximación simple garantiza para cada función continua la existencia de una aproximación simple al menos después del refinamiento de , por ejemplo reemplazando por su subdivisión baricéntrica iterada. ^[2] El teorema juega un papel importante en ciertos enunciados de topología algebraica para reducir el comportamiento de aplicaciones continuas respecto de aplicaciones simpliciales, por ejemplo en el teorema del punto fijo de Lefschetz. ${\displaystyle f:V_{K}\rightarrow V_{L}}$ ${\displaystyle {\mathcal {K}}}$ ${\displaystyle {\mathcal {K}}}$

Teorema del punto fijo de Lefschetz

El número de Lefschetz es una herramienta útil para saber si una función continua admite puntos fijos. Estos datos se calculan de la siguiente manera: Supongamos que y son espacios topológicos que admiten triangulaciones finitas. Un mapa continuo induce homomorfismos entre sus grupos de homología simplicial con coeficientes en un campo . Estos son mapas lineales entre espacios vectoriales, por lo que se puede determinar su traza y su suma alterna. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f:X\rightarrow Y}$ ${\displaystyle f_{i}:H_{i}(X,K)\rightarrow H_{i}(Y,K)}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle tr_{i}}$

${\displaystyle L_{K}(f)=\sum _{i}(-1)^{i}tr_{i}(f)\in K}$

se llama número de Lefschetz . Si , este número es la característica de Euler de . El teorema del punto fijo establece que siempre que , tiene un punto fijo. En la prueba, esto se muestra primero sólo para aplicaciones simpliciales y luego se generaliza para cualquier función continua mediante el teorema de aproximación. El teorema del punto fijo de Brouwer trata el caso en el que existe un endomorfismo de la bola unitaria. Porque todos sus grupos de homología desaparecen y siempre es la identidad, por lo que tiene un punto fijo. ^[20] ${\displaystyle f}$ ${\displaystyle f=id}$ ${\displaystyle K}$ ${\displaystyle L_{K}(f)\neq 0}$ ${\displaystyle f}$ ${\displaystyle f:\mathbb {D} ^{n}\rightarrow \mathbb {D} ^{n}}$ ${\displaystyle k\geq 1}$ ${\displaystyle H_{k}(\mathbb {D} ^{n})}$ ${\displaystyle f_{0}}$ ${\displaystyle L_{K}(f)=tr_{0}(f)=1\neq 0}$ ${\displaystyle f}$

Fórmula de Riemann-Hurwitz

La fórmula de Riemann-Hurwitz permite determinar el género de una superficie de Riemann compacta y conexa sin utilizar una triangulación explícita. La prueba necesita la existencia de triangulaciones para superficies en un sentido abstracto: Sea una función holomorfa no constante sobre una superficie con género conocido. La relación entre el género de las superficies y es. ${\displaystyle X}$ ${\displaystyle F:X\rightarrow Y}$ ${\displaystyle g}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle 2g(X)-2=deg(F)(2g(Y)-2)\sum _{x\in X}(ord(F)-1)}$

donde denota el grado del mapa. La suma está bien definida ya que solo cuenta los puntos ramificados de la función. ${\displaystyle deg(F)}$

El trasfondo de esta fórmula es que las funciones holomorfas en las superficies de Riemann son recubrimientos ramificados. La fórmula se puede encontrar examinando la imagen de la estructura simple cerca de los puntos de ramificación. ^[21]

Citas

1. John M. Lee (2000), Springer Verlag (ed.), Introducción a las variedades topológicas (en alemán), Nueva York/Berlín/Heidelberg: Springer Verlag, p. 92, ISBN 0-387-98759-2
2. James R. Munkres (1984), Elementos de topología algebraica (en alemán), vol. 1984, Menlo Park, California: Addison Wesley, pág. 83, ISBN 0-201-04586-9
3. JHC Whitehead (1940), "On C1-Complexes", Annals of Mathematics (en alemán), vol. 41, núm. 4, págs. 809–824, doi :10.2307/1968861, ISSN  0003-486X, JSTOR  1968861
4. JW Alexander (1926), "Combinatorial Analysis Situs", Transactions of the American Mathematical Society (en alemán), vol. 28, núm. 2, págs. 301–329, doi : 10.1090/S0002-9947-1926-1501346-5 , ISSN  0002-9947, JSTOR  1989117
5. R. Stöcker, H. Zieschang (1994), Algebraische Topologie (en alemán) (2. überarbeitete ed.), Stuttgart: BGTeubner, p. 270, ISBN 3-519-12226-X
6. Allen Hatcher (2006), Topología algebraica (en alemán), Cambridge/Nueva York/Melbourne: Cambridge University Press, p. 110, ISBN 0-521-79160--X
7. AARanicki. "Uno de los Hauptvermutung" (PDF) . El libro Hauptvermutung .
8. John Milnor (1961), "Dos complejos que son homeomórficos pero combinatoriamente distintos", The Annals of Mathematics (en alemán), vol. 74, núm. 3, pág. 575, doi :10.2307/1970299, ISSN  0003-486X, JSTOR  1970299
9. Marshall M. Cohen (1973), "Un curso de teoría de la homotopía simple", Textos de posgrado en matemáticas , Textos de posgrado en matemáticas (en alemán), vol. 10, doi :10.1007/978-1-4684-9372-6, ISBN 978-0-387-90055-1, ISSN  0072-5285
10. Edwin Moise (1977), Topología geométrica en dimensiones 2 y 3 (en alemán), Nueva York: Springer Verlag
11. Tibor Rado. "Über den Begriff der Riemannschen Fläche" (PDF) .
12. RC Kirby, LC Siebenmann (31 de diciembre de 1977), "Anexo B. Sobre la triangulación de variedades y la Hauptvermutung", Ensayos fundamentales sobre variedades, suavizados y triangulaciones topológicas. (AM-88) (en alemán), Princeton University Press, págs. 299–306
13. "Capítulo IV; Invariante de Casson para tres esferas de homología orientada", Invariante de Casson para tres esferas de homología orientada (en alemán), Princeton University Press, págs. 63–79, 1990-12-31
14. Toenniessen, Fridtjof (2017), Topologie (PDF) (en alemán), doi :10.1007/978-3-662-54964-3, ISBN 978-3-662-54963-6, recuperado el 20 de abril de 2022
15. Edwin E. Moise (1952), "Estructuras afines en 3 variedades: V. El teorema de la triangulación y Hauptvermutung", The Annals of Mathematics (en alemán), vol. 56, núm. 1, pág. 96, doi :10.2307/1969769, ISSN  0003-486X, JSTOR  1969769
16. Robert D. Edwards (18 de octubre de 2006), "Suspensiones de esferas de homología", arXiv:math/0610573 (en alemán), arXiv : math/0610573 , Bibcode :2006math.....10573E
17. WBR Lickorish (20 de noviembre de 1999), "Movimientos simples en complejos y variedades", Actas del Kirbyfest (en alemán), Mathematical Sciences Publishers, arXiv : math/9911256 , doi :10.2140/gtm.1999.2.299, S2CID  9765634
18. Toenniessen, Fridtjof (2017), Topologie (PDF) (en alemán), p. 315, doi :10.1007/978-3-662-54964-3, ISBN 978-3-662-54963-6, recuperado el 20 de abril de 2022
19. Seifert, H. (Herbert), 1907-1996. (2003), Lehrbuch der Topologie (en alemán), AMS Chelsea Pub., ISBN 0-8218-3595-5{{citation}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
20. Bredon, Glen E. (1993), Springer Verlag (ed.), Topología y geometría (en alemán), Berlín/Heidelberg/Nueva York, págs. 254 y siguientes, ISBN 3-540-97926-3{{citation}}: CS1 maint: location missing publisher (link)
21. Otto Forster (1977), "Kompakte Riemannsche Flächen", Heidelberger Taschenbücher (en alemán), Berlín, Heidelberg: Springer Berlin Heidelberg, págs. 88-154, ISBN 978-3-540-08034-3

Ver también

• Triangulación (geometría)
• Malla triangular

Literatura

• Allen Hatcher: Topología algebraica , Cambridge University Press, Cambridge/Nueva York/Melbourne 2006, ISBN 0-521-79160-X
• James R. Munkres: . Banda 1984. Addison Wesley, Menlo Park, California 1984, ISBN 0-201-04586-9
• Marshall M. Cohen: un curso de teoría de la homotopía simple . En: Textos de Posgrado en Matemáticas . 1973, ISSN 0072-5285, doi :10.1007/978-1-4684-9372-6.