En electrónica y telecomunicaciones , la conformación de pulsos es el proceso de cambiar la forma de onda de los pulsos transmitidos para optimizar la señal para su propósito previsto o el canal de comunicación . Esto se hace a menudo limitando el ancho de banda de la transmisión y filtrando los pulsos para controlar la interferencia entre símbolos . La conformación de pulsos es particularmente importante en la comunicación de RF para ajustar la señal dentro de una determinada banda de frecuencia y normalmente se aplica después de la codificación y modulación de línea .
La transmisión de una señal a una alta tasa de modulación a través de un canal de banda limitada puede crear interferencias intersimbólicas . La razón de esto son las correspondencias de Fourier (ver transformada de Fourier ). Una señal de banda limitada corresponde a una señal de tiempo infinito, que hace que los pulsos vecinos se superpongan. A medida que aumenta la tasa de modulación, aumenta el ancho de banda de la señal. [1] Tan pronto como el espectro de la señal es un rectángulo agudo, esto conduce a una forma sinc en el dominio del tiempo. Esto sucede si el ancho de banda de la señal es mayor que el ancho de banda del canal, lo que conduce a una distorsión. Esta distorsión generalmente se manifiesta como interferencia intersimbólica (ISI). Teóricamente, para pulsos con forma sinc, no hay ISI, si los pulsos vecinos están perfectamente alineados, es decir, en los cruces por cero entre sí. Pero esto requiere una muy buena sincronización y un muestreo preciso/estable sin fluctuaciones. Como herramienta práctica para determinar la ISI, se utiliza el patrón de ojo , que visualiza los efectos típicos del canal y la estabilidad de sincronización/frecuencia.
El espectro de la señal está determinado por el esquema de modulación y la velocidad de datos que utiliza el transmisor, pero se puede modificar con un filtro de modelado de pulsos. Este modelado de pulsos suavizará el espectro, lo que dará lugar a una señal limitada en el tiempo nuevamente. Por lo general, los símbolos transmitidos se representan como una secuencia temporal de pulsos delta de Dirac multiplicados por el símbolo. Esta es la transición formal del dominio digital al analógico. En este punto, el ancho de banda de la señal es ilimitado. Esta señal teórica se filtra luego con el filtro de modelado de pulsos, lo que produce la señal transmitida. Si el filtro de modelado de pulsos es rectangular en el dominio del tiempo (como se suele hacer al dibujarlo), esto daría lugar a un espectro ilimitado.
En muchos sistemas de comunicación de banda base, el filtro de conformación de pulsos es implícitamente un filtro boxcar . Su transformada de Fourier tiene la forma sen(x)/x y tiene una potencia de señal significativa a frecuencias superiores a la velocidad de símbolo. Esto no es un gran problema cuando se utiliza fibra óptica o incluso un cable de par trenzado como canal de comunicación. Sin embargo, en las comunicaciones de RF esto desperdiciaría ancho de banda y solo se utilizan bandas de frecuencia estrictamente especificadas para transmisiones individuales. En otras palabras, el canal para la señal está limitado en banda. Por lo tanto, se han desarrollado mejores filtros, que intentan minimizar el ancho de banda necesario para una determinada velocidad de símbolo.
Un ejemplo en otras áreas de la electrónica es la generación de pulsos donde el tiempo de subida debe ser corto; una forma de hacerlo es comenzar con un pulso de subida más lenta y disminuir el tiempo de subida, por ejemplo con un circuito de diodo de recuperación escalonada .
Estas descripciones proporcionan un conocimiento práctico que cubre la mayoría de los efectos, pero no incluyen la causalidad, que daría lugar a funciones/señales analíticas. Para comprender esto completamente, se necesita la transformada de Hilbert , que induce una dirección mediante la convolución con el núcleo de Cauchy. Esto acopla la parte real e imaginaria de la descripción de la banda base, agregando así estructura. Esto implica inmediatamente que tanto la parte real como la imaginaria son suficientes para describir una señal analítica. Al medir ambas en un entorno ruidoso, se tiene una redundancia que se puede utilizar para reconstruir mejor la señal original. Una realización física siempre es causal, ya que una señal analítica transporta la información.

No todos los filtros pueden utilizarse como filtros de modelado de pulsos. El filtro en sí no debe introducir interferencias entre símbolos; debe cumplir ciertos criterios. El criterio ISI de Nyquist es un criterio de evaluación que se utiliza con frecuencia, ya que relaciona el espectro de frecuencia de la señal del transmisor con la interferencia entre símbolos.
Algunos ejemplos de filtros de modelado de pulsos que se encuentran comúnmente en los sistemas de comunicación son:
La conformación de pulsos del lado del transmisor se combina a menudo con un filtro adaptado del lado del receptor para lograr una tolerancia óptima al ruido en el sistema. En este caso, la conformación de pulsos se distribuye de manera uniforme entre los filtros del transmisor y del receptor. Las respuestas de amplitud de los filtros son, por lo tanto, raíces cuadradas puntuales de los filtros del sistema.
Se han inventado otros enfoques que eliminan los filtros complejos de modelado de pulsos. En OFDM , las portadoras se modulan tan lentamente que cada una de ellas prácticamente no se ve afectada por la limitación del ancho de banda del canal.
También se le denomina filtro Boxcar, ya que su equivalente en el dominio de frecuencia es una forma rectangular. En teoría, el mejor filtro de modelado de pulsos sería el filtro sinc, pero no se puede implementar con precisión. Es un filtro no causal con colas que decaen relativamente lentamente. También es problemático desde el punto de vista de la sincronización, ya que cualquier error de fase da como resultado una interferencia entre símbolos que aumenta considerablemente.
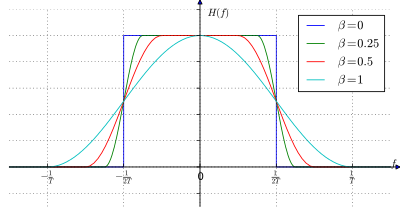
El coseno elevado es similar al sinc, con la compensación de lóbulos laterales más pequeños por un ancho espectral ligeramente mayor. Los filtros de coseno elevado son prácticos de implementar y se utilizan ampliamente. Tienen un ancho de banda excedente configurable, por lo que los sistemas de comunicación pueden elegir un equilibrio entre un filtro más simple y la eficiencia espectral.
Esto proporciona un pulso de salida con forma de función gaussiana .