Microlente gravitacional

Fenómeno astronómico debido al efecto de lente gravitacional

La microlente gravitacional es un fenómeno astronómico causado por el efecto de lente gravitacional . Puede utilizarse para detectar objetos que van desde la masa de un planeta hasta la masa de una estrella, independientemente de la luz que emitan. Normalmente, los astrónomos solo pueden detectar objetos brillantes que emiten mucha luz ( estrellas ) u objetos grandes que bloquean la luz de fondo (nubes de gas y polvo). Estos objetos constituyen solo una pequeña porción de la masa de una galaxia. ^{[ aclaración necesaria ]} La microlente permite el estudio de objetos que emiten poca o ninguna luz.

Microlente gravitacional de la luz de una estrella distante de fondo por un exoplaneta rebelde que pasa cerca

Microlente gravitacional de la luz de una estrella de fondo distante por un exoplaneta que pasa con una estrella anfitriona

Cuando una estrella distante o un quásar se alinea lo suficiente con un objeto masivo y compacto en primer plano, la curvatura de la luz debida a su campo gravitatorio, como lo analizó Albert Einstein en 1915, produce dos imágenes distorsionadas (generalmente sin resolución ), lo que da como resultado un aumento observable. La escala temporal del aumento transitorio del brillo depende de la masa del objeto en primer plano, así como del movimiento propio relativo entre la "fuente" de fondo y el objeto "lente" en primer plano.

La microlente alineada idealmente produce un claro amortiguador entre la radiación de la lente y los objetos fuente. Amplía la fuente distante, revelándola o mejorando su tamaño y/o brillo. Permite el estudio de la población de objetos débiles u oscuros como enanas marrones , enanas rojas , planetas , enanas blancas , estrellas de neutrones , agujeros negros y objetos masivos compactos con halo . Este tipo de lente funciona en todas las longitudes de onda, ampliando y produciendo una amplia gama de posibles deformaciones para objetos fuente distantes que emiten cualquier tipo de radiación electromagnética.

La microlente producida por un objeto aislado se detectó por primera vez en 1989. Desde entonces, la microlente se ha utilizado para limitar la naturaleza de la materia oscura , detectar exoplanetas , estudiar el oscurecimiento de los limbos en estrellas distantes, limitar la población de estrellas binarias y limitar la estructura del disco de la Vía Láctea. La microlente también se ha propuesto como un medio para encontrar objetos oscuros como enanas marrones y agujeros negros, estudiar manchas estelares , medir la rotación estelar y sondear cuásares ^{[1] [2]} incluidos sus discos de acreción . ^{[3] [4] [5] [6]} La microlente se utilizó en 2018 para detectar Ícaro , entonces la estrella más distante jamás observada. ^{[7] [8]}

Cómo funciona

La microlente se basa en el efecto de lente gravitacional . Un objeto masivo (la lente) desvía la luz de un objeto brillante de fondo (la fuente). Esto puede generar múltiples imágenes distorsionadas, ampliadas y más brillantes de la fuente de fondo. ^[9]

La microlente es causada por el mismo efecto físico que la lente gravitacional fuerte y la lente gravitacional débil , pero se estudia mediante técnicas de observación muy diferentes. En la lente fuerte y débil, la masa de la lente es lo suficientemente grande (masa de una galaxia o cúmulo de galaxias) como para que el desplazamiento de la luz por la lente se pueda resolver con un telescopio de alta resolución como el Telescopio Espacial Hubble . Con la microlente, la masa de la lente es demasiado baja (masa de un planeta o una estrella) para que se observe fácilmente el desplazamiento de la luz, pero aún se puede detectar el brillo aparente de la fuente. En tal situación, la lente pasará por la fuente en una cantidad de tiempo razonable, segundos a años en lugar de millones de años. A medida que cambia la alineación, cambia el brillo aparente de la fuente, y esto se puede monitorear para detectar y estudiar el evento. Por lo tanto, a diferencia de las lentes gravitacionales fuertes y débiles, la microlente es un evento astronómico transitorio desde una perspectiva de escala de tiempo humana, ^[10] por lo tanto un tema de astronomía de dominio del tiempo .

A diferencia de lo que ocurre con el efecto de lente fuerte y débil, ninguna observación individual puede establecer que se está produciendo un efecto de microlente. En cambio, el aumento y la caída del brillo de la fuente deben controlarse a lo largo del tiempo mediante fotometría . Esta función del brillo en función del tiempo se conoce como curva de luz . A continuación se muestra una curva de luz de microlente típica:

Curva de luz típica del evento de microlente gravitacional (OGLE-2005-BLG-006) con su modelo ajustado (rojo)

Un fenómeno típico de microlente como éste tiene una forma muy simple y solo se puede extraer un parámetro físico: la escala de tiempo, que está relacionada con la masa, la distancia y la velocidad de la lente. Sin embargo, hay varios efectos que contribuyen a la forma de fenómenos de microlente más atípicos:

• Distribución de la masa de la lente. Si la masa de la lente no está concentrada en un único punto, la curva de luz puede ser muy diferente, en particular en el caso de eventos de cruce de cáusticos , que pueden presentar picos fuertes en la curva de luz. En la microlente, esto se puede ver cuando la lente es una estrella binaria o un sistema planetario .
• Tamaño finito de la fuente. En fenómenos de microlente extremadamente brillantes o que cambian rápidamente, como los fenómenos de cruce cáustico, la estrella fuente no puede ser tratada como un punto de luz infinitesimalmente pequeño: el tamaño del disco de la estrella e incluso el oscurecimiento del limbo pueden modificar las características extremas.
• Paralaje . En el caso de eventos que duran meses, el movimiento de la Tierra alrededor del Sol puede provocar que la alineación cambie ligeramente, lo que afecta la curva de luz.

Actualmente, la mayor parte de la atención se centra en los fenómenos de microlente más inusuales, especialmente aquellos que podrían conducir al descubrimiento de planetas extrasolares.

Otra forma de obtener más información de los eventos de microlente implica medir los cambios astrométricos en la posición de la fuente durante el curso del evento ^[11] e incluso resolver las imágenes separadas con interferometría . ^[12] La primera resolución exitosa de imágenes de microlente se logró con el instrumento GRAVITY en el Interferómetro del Very Large Telescope (VLTI) . ^[13] Cuando las dos imágenes de la fuente no están resueltas (es decir, no son detectables por separado por los instrumentos disponibles), la posición medida es un promedio de las dos posiciones, ponderada por su brillo. Esto se llama la posición del centroide . Si la fuente está, digamos, muy a la "derecha" de la lente, entonces una imagen estará muy cerca de la posición real de la fuente y la otra estará muy cerca de la lente en su lado izquierdo, y muy pequeña o tenue. En este caso, el centroide está prácticamente en la misma posición que la fuente. Si la posición de la fuente en el cielo es cercana a la de la lente y a la derecha, la imagen principal estará un poco más a la derecha de la posición real de la fuente, y el centroide estará a la derecha de la posición real. Pero a medida que la fuente se acerca aún más en el cielo a la posición de la lente, las dos imágenes se vuelven simétricas e iguales en brillo, y el centroide volverá a estar muy cerca de la posición real de la fuente. Cuando la alineación es perfecta, el centroide está exactamente en la misma posición que la fuente (y la lente). En este caso, no habrá dos imágenes sino un anillo de Einstein alrededor de la lente. ^{[14] [15]}

Observación de microlente

El objeto que causa el efecto microlente en NGC 6553 desvió la luz de una estrella gigante roja en el fondo. ^{[16] [17]}

En la práctica, debido a que la alineación necesaria es tan precisa y difícil de predecir, la microlente es muy poco frecuente. Por lo tanto, los eventos se encuentran generalmente con estudios que monitorean fotométricamente decenas de millones de estrellas fuente potenciales, cada pocos días durante varios años. Los campos de fondo densos adecuados para tales estudios son las galaxias cercanas, como las Nubes de Magallanes y la galaxia de Andrómeda, y el bulbo de la Vía Láctea.

Eventos de microlente sobre el mapa galáctico observados por GAIA entre 2014 y 2018 ^{[18] [19]} (Temporizador en la esquina inferior izquierda)

En cada caso, la población de lentes estudiada comprende los objetos entre la Tierra y el campo fuente: para el bulbo, la población de lentes son las estrellas del disco de la Vía Láctea, y para las galaxias externas, la población de lentes es el halo de la Vía Láctea, así como los objetos en la otra galaxia misma. La densidad, masa y ubicación de los objetos en estas poblaciones de lentes determina la frecuencia de microlente a lo largo de esa línea de visión, que se caracteriza por un valor conocido como profundidad óptica debido a la microlente. (Esto no debe confundirse con el significado más común de profundidad óptica , aunque comparte algunas propiedades). La profundidad óptica es, en términos generales, la fracción promedio de estrellas fuente que experimentan microlente en un momento dado, o equivalentemente la probabilidad de que una estrella fuente dada esté experimentando efecto de lente en un momento dado. El proyecto MACHO descubrió que la profundidad óptica hacia la LMC era de 1,2×10 −7 ^{[ 20]} y la profundidad óptica hacia el bulbo era de 2,43×10 ⁻⁶ o aproximadamente 1 en 400 000. ^[21]

Lo que complica la búsqueda es el hecho de que por cada estrella que experimenta microlente, hay miles de estrellas que cambian de brillo por otras razones (alrededor del 2% de las estrellas en un campo fuente típico son estrellas naturalmente variables ) y otros eventos transitorios (como novas y supernovas ), y estos deben eliminarse para encontrar verdaderos eventos de microlente. Una vez que se ha identificado un evento de microlente en curso, el programa de monitoreo que lo detecta a menudo alerta a la comunidad sobre su descubrimiento, de modo que otros programas especializados puedan seguir el evento más intensamente, con la esperanza de encontrar desviaciones interesantes de la curva de luz típica. Esto se debe a que estas desviaciones, en particular las debidas a exoplanetas, requieren un monitoreo horario para ser identificadas, que los programas de estudio no pueden proporcionar mientras siguen buscando nuevos eventos. La cuestión de cómo priorizar los eventos en curso para un seguimiento detallado con recursos de observación limitados es muy importante para los investigadores de microlente en la actualidad.

Historia

Ya en su libro The Queries (consulta número 1), ampliado de 1704 a 1718, Isaac Newton se preguntó si un rayo de luz podría ser desviado por la gravedad. En 1801, Johann Georg von Soldner calculó la cantidad de desviación de un rayo de luz de una estrella bajo la gravedad newtoniana. En 1915, Albert Einstein predijo correctamente la cantidad de desviación bajo la Relatividad General , que era el doble de la cantidad predicha por von Soldner. La predicción de Einstein fue validada por una expedición de 1919 dirigida por Arthur Eddington , que fue un gran éxito temprano para la Relatividad General. ^[22] En 1924, Orest Chwolson descubrió que el efecto de lente podía producir múltiples imágenes de la estrella. En 1936, Einstein publicó una predicción correcta del brillo concomitante de la fuente, la base del efecto de microlente. ^[23] Debido a la improbable alineación requerida, concluyó que "no hay grandes posibilidades de observar este fenómeno". El marco teórico moderno de la lente gravitacional se estableció con los trabajos de Yu Klimov (1963), Sidney Liebes (1964) y Sjur Refsdal (1964). ^[1]

El efecto de lente gravitacional se observó por primera vez en 1979, en forma de un cuásar afectado por una galaxia en primer plano. Ese mismo año, Kyongae Chang y Sjur Refsdal demostraron que las estrellas individuales en la galaxia de la lente podían actuar como lentes más pequeñas dentro de la lente principal, lo que causaba que las imágenes del cuásar fuente fluctuaran en una escala de tiempo de meses, también conocida como lente Chang-Refsdal . ^[24] Peter J. Young se dio cuenta de que era necesario ampliar el análisis para permitir el efecto simultáneo de muchas estrellas. ^[25] Bohdan Paczyński utilizó por primera vez el término "microlente" para describir este fenómeno. Este tipo de microlente es difícil de identificar debido a la variabilidad intrínseca de los cuásares, pero en 1989 Mike Irwin et al. publicaron la detección de microlente de una de las cuatro imágenes en el cuásar " Cruz de Einstein " en la Lente de Huchra . ^[26]

En 1986, Paczyński propuso utilizar la microlente para buscar materia oscura en forma de objetos masivos compactos de halo ( MACHO ) en el halo galáctico , observando estrellas de fondo en una galaxia cercana. Dos grupos de físicos de partículas que trabajaban en materia oscura escucharon sus charlas y se unieron a los astrónomos para formar la colaboración anglo-australiana MACHO y la colaboración francesa EROS. ^{[ cita requerida ]}

En 1986, Robert J. Nemiroff predijo la probabilidad de microlente ^[27] y calculó curvas básicas de luz inducida por microlente para varias configuraciones posibles de fuente de lente en su tesis de 1987. ^[28]

En 1991, Mao y Paczyński sugirieron que la microlente podría usarse para encontrar compañeros binarios de estrellas, y en 1992 Gould y Loeb demostraron que la microlente puede usarse para detectar exoplanetas. En 1992, Paczyński fundó el Experimento de Lente Gravitacional Óptica , que comenzó a buscar eventos en la dirección del bulbo galáctico . Los primeros dos eventos de microlente en la dirección de la Gran Nube de Magallanes que podrían ser causados ​​por materia oscura fueron informados en artículos consecutivos en Nature por MACHO ^[29] y EROS ^[30] en 1993, y en los años siguientes, se siguieron detectando eventos. Durante este tiempo, Sun Hong Rhie trabajó en la teoría de la microlente de exoplanetas para eventos del estudio. La colaboración MACHO terminó en 1999. Sus datos refutaron la hipótesis de que el 100% del halo oscuro está compuesto por MACHO, pero encontraron un exceso significativo e inexplicable de aproximadamente el 20% de la masa del halo, que podría deberse a los MACHO o a lentes dentro de la propia Gran Nube de Magallanes. ^[31]

Posteriormente, EROS publicó límites superiores aún más estrictos para los MACHO ^[32] y actualmente no se sabe con certeza si existe algún exceso de microlente de halo que pueda deberse a la materia oscura. El proyecto SuperMACHO, actualmente en marcha, busca localizar las lentes responsables de los resultados de MACHO. ^{[ cita requerida ]}

A pesar de no resolver el problema de la materia oscura, se ha demostrado que la microlente es una herramienta útil para muchas aplicaciones. Se detectan cientos de eventos de microlente por año hacia el bulbo galáctico , donde la profundidad óptica de la microlente (debido a las estrellas en el disco galáctico) es aproximadamente 20 veces mayor que a través del halo galáctico. En 2007, el proyecto OGLE identificó 611 candidatos a eventos, y el proyecto MOA (una colaboración Japón-Nueva Zelanda) ^[33] identificó 488 (aunque no todos los candidatos resultan ser eventos de microlente, y existe una superposición significativa entre los dos proyectos). Además de estos estudios, se están llevando a cabo proyectos de seguimiento para estudiar en detalle eventos potencialmente interesantes en curso, principalmente con el objetivo de detectar planetas extrasolares. ^{[ cita requerida ]} Estos incluyen MiNDSTEp, ^[34] RoboNet, ^[35] MicroFUN ^[36] y PLANET. ^[37]

En septiembre de 2020, los astrónomos que utilizan técnicas de microlente informaron la detección , por primera vez, de un planeta rebelde con una masa similar a la de la Tierra, no limitado por ninguna estrella y que flota libremente en la Vía Láctea . ^{[38] [39]}

La microlente no solo magnifica la fuente sino que también desplaza su posición aparente. La duración de esta es mayor que la del aumento, y puede utilizarse para hallar la masa de la lente. En 2022 se informó de que esta técnica se utilizó para realizar la primera detección inequívoca de un agujero negro aislado de masa estelar , utilizando observaciones del telescopio espacial Hubble que se extendieron durante seis años, comenzando en agosto de 2011 poco después de que se detectara el evento de microlente. El agujero negro tiene una masa de unas 7 veces la masa solar y se encuentra a unos 1,6 kiloparsecs (5,2 kly) de distancia, en Sagitario , mientras que la estrella está a unos 6 kiloparsecs (20 kly) de distancia. Hay millones de agujeros negros aislados en nuestra galaxia, y al estar aislados se emite muy poca radiación desde sus alrededores, por lo que solo pueden detectarse mediante microlente. Los autores esperan que se encuentren muchos más con futuros instrumentos, en concreto el telescopio espacial Nancy Grace Roman y el observatorio Vera C. Rubin . ^[14]

Matemáticas

^{Gould [40]} describe las matemáticas de la microlente junto con la notación moderna, y en esta sección utilizamos su notación, aunque otros autores han utilizado otra notación. El radio de Einstein , también llamado ángulo de Einstein, es el radio angular del anillo de Einstein en caso de alineación perfecta. Depende de la masa de la lente M, la distancia de la lente d _L y la distancia de la fuente d _S :

${\displaystyle \theta _{E}={\sqrt {{\frac {4GM}{c^{2}}}{\frac {d_{S}-d_{L}}{d_{S}d_{L}}}}}}$(en radianes).

Para M igual a 60 masas de Júpiter , d _L = 4000 parsecs y d _S = 8000 parsecs (típico para un evento de microlente del Bulbo), el radio de Einstein es 0,00024 segundos de arco ^[41] ( ángulo subtendido por 1 au a 4000 parsecs). ^[42] En comparación, las observaciones ideales basadas en la Tierra tienen una resolución angular de alrededor de 0,4 segundos de arco, 1660 veces mayor. Dado que es tan pequeño, generalmente no se observa para un evento de microlente típico, pero se puede observar en algunos eventos extremos como se describe a continuación. ${\displaystyle \theta _{E}}$

Aunque no hay un principio ni un final claros de un evento de microlente, por convención se dice que el evento dura mientras la separación angular entre la fuente y la lente sea menor que . Por lo tanto, la duración del evento está determinada por el tiempo que tarda el movimiento aparente de la lente en el cielo en cubrir una distancia angular . El radio de Einstein también es del mismo orden de magnitud que la separación angular entre las dos imágenes de la lente y el cambio astrométrico de las posiciones de la imagen a lo largo del curso del evento de microlente. ${\displaystyle \theta _{E}}$ ${\displaystyle \theta _{E}}$

Durante un evento de microlente, el brillo de la fuente se amplifica mediante un factor de amplificación A. Este factor depende únicamente de la proximidad de la alineación entre el observador, la lente y la fuente. El número sin unidades u se define como la separación angular de la lente y la fuente, dividida por . El factor de amplificación se da en términos de este valor: ^[43] ${\displaystyle \theta _{E}}$

${\displaystyle A(u)={\frac {u^{2}+2}{u{\sqrt {u^{2}+4}}}}.}$

Esta función tiene varias propiedades importantes. A(u) es siempre mayor que 1, por lo que la microlente solo puede aumentar el brillo de la estrella fuente, no disminuirlo. A(u) siempre disminuye a medida que u aumenta, por lo que cuanto más cerca esté la alineación, más brillante se vuelve la fuente. A medida que u se acerca al infinito, A(u) se acerca a 1, de modo que en separaciones amplias, la microlente no tiene efecto. Finalmente, a medida que u se acerca a 0, para una fuente puntual A(u) se acerca al infinito a medida que las imágenes se acercan a un anillo de Einstein. Para una alineación perfecta (u = 0), A(u) es teóricamente infinita. En la práctica, los objetos del mundo real no son fuentes puntuales, y los efectos del tamaño finito de la fuente establecerán un límite a cuán grande puede ocurrir una amplificación para una alineación muy cercana, ^[44] pero algunos eventos de microlente pueden causar un brillo por un factor de cientos.

A diferencia de la macrolente gravitacional, en la que la lente es una galaxia o un cúmulo de galaxias, en la microlente u cambia significativamente en un corto período de tiempo. La escala de tiempo relevante se denomina tiempo de Einstein y está dada por el tiempo que tarda la lente en recorrer una distancia angular relativa a la fuente en el cielo. Para los eventos típicos de microlente, es del orden de unos pocos días a unos pocos meses. La función u(t) se determina simplemente mediante el teorema de Pitágoras: ${\displaystyle t_{E}}$ ${\displaystyle \theta _{E}}$ ${\displaystyle t_{E}}$

${\displaystyle u(t)={\sqrt {u_{min}^{2}+\left({\frac {t-t_{0}}{t_{E}}}\right)^{2}}}.}$

El valor mínimo de u, llamado u _min , determina el brillo máximo del evento.

En un evento típico de microlente, la curva de luz se ajusta bien al suponer que la fuente es un punto, la lente es una masa puntual única y la lente se mueve en línea recta: la aproximación de fuente puntual-lente puntual . En estos eventos, el único parámetro físicamente significativo que se puede medir es la escala de tiempo de Einstein . Dado que este observable es una función degenerada de la masa, la distancia y la velocidad de la lente, no podemos determinar estos parámetros físicos a partir de un solo evento. ${\displaystyle t_{E}}$

Sin embargo, en algunos eventos extremos, puede ser medible mientras que otros eventos extremos pueden investigar un parámetro adicional: el tamaño del anillo de Einstein en el plano del observador, conocido como el radio de Einstein proyectado : . Este parámetro describe cómo el evento parecerá diferente desde dos observadores en diferentes ubicaciones, como un observador satelital. El radio de Einstein proyectado está relacionado con los parámetros físicos de la lente y la fuente por ${\displaystyle \theta _{E}}$ ${\displaystyle {\tilde {r}}_{E}}$

${\displaystyle {\tilde {r}}_{E}={\sqrt {{\frac {4GM}{c^{2}}}{\frac {d_{S}d_{L}}{d_{S}-d_{L}}}}}.}$

Resulta matemáticamente conveniente utilizar las inversas de algunas de estas cantidades. Se trata del movimiento propio de Einstein.

${\displaystyle {\vec {\mu }}_{E}={t_{E}}^{-1}}$

y la paralaje de Einstein

${\displaystyle {\vec {\pi }}_{E}={{\tilde {r}}_{E}}^{-1}.}$

Estas magnitudes vectoriales apuntan en la dirección del movimiento relativo de la lente con respecto a la fuente. Algunos eventos de microlente extremos solo pueden restringir un componente de estas magnitudes vectoriales. Si se midieran completamente estos parámetros adicionales, se pueden resolver los parámetros físicos de la lente y obtener la masa, la paralaje y el movimiento propio de la lente como

${\displaystyle M={\frac {c^{2}}{4G}}\theta _{E}{\tilde {r}}_{E},}$

${\displaystyle \pi _{L}=\pi _{E}\theta _{E}+\pi _{S},}$

${\displaystyle \mu _{L}=\mu _{E}\theta _{E}+\mu _{S}.}$

Eventos de microlente extrema

En un evento típico de microlente, la curva de luz se ajusta bien al suponer que la fuente es un punto, la lente es una masa puntual única y la lente se mueve en línea recta: la aproximación de fuente puntual-lente puntual . En estos eventos, el único parámetro físicamente significativo que se puede medir es la escala de tiempo de Einstein . Sin embargo, en algunos casos, los eventos se pueden analizar para obtener los parámetros adicionales del ángulo de Einstein y la paralaje: y . Estos incluyen eventos de aumento muy alto, lentes binarias, paralaje y eventos xallarap, y eventos donde la lente es visible. ${\displaystyle t_{E}}$ ${\displaystyle \theta _{E}}$ ${\displaystyle \pi _{E}}$

Eventos que dieron lugar al ángulo de Einstein

Aunque el ángulo de Einstein es demasiado pequeño para ser visible directamente desde un telescopio terrestre, se han propuesto varias técnicas para observarlo.

Si la lente pasa directamente frente a la estrella fuente, entonces el tamaño finito de la estrella fuente se convierte en un parámetro importante. La estrella fuente debe tratarse como un disco en el cielo, no como un punto, rompiendo la aproximación de fuente puntual y causando una desviación de la curva de microlente tradicional que dura tanto como el tiempo que tarda la lente en cruzar la fuente, conocida como curva de luz de fuente finita . La longitud de esta desviación se puede utilizar para determinar el tiempo que necesita la lente para cruzar el disco de la estrella fuente . Si se conoce el tamaño angular de la fuente , el ángulo de Einstein se puede determinar como ${\displaystyle t_{S}}$ ${\displaystyle \theta _{S}}$

${\displaystyle \theta _{E}=\theta _{S}{\frac {t_{E}}{t_{S}}}.}$

Estas mediciones son poco frecuentes, ya que requieren una alineación extrema entre la fuente y la lente. Es más probable que se realicen cuando la fuente es (relativamente) grande, es decir, para fuentes gigantes cercanas con lentes de baja masa y movimiento lento cerca de la fuente. ${\displaystyle \theta _{S}/\theta _{E}}$

En los eventos de fuente finita, las distintas partes de la estrella fuente se magnifican a distintas velocidades en distintos momentos durante el evento. Por lo tanto, estos eventos se pueden utilizar para estudiar el oscurecimiento del borde de la estrella fuente.

Lentes binarias

Si la lente es una estrella binaria con una separación de aproximadamente el radio de Einstein, el patrón de aumento es más complejo que en las lentes de estrellas individuales. En este caso, normalmente hay tres imágenes cuando la lente está alejada de la fuente, pero hay un rango de alineaciones donde se crean dos imágenes adicionales. Estas alineaciones se conocen como cáusticas . En estas alineaciones, el aumento de la fuente es formalmente infinito bajo la aproximación de fuente puntual. ^{[ cita requerida ]}

Los cruces cáusticos en lentes binarias pueden ocurrir con una gama más amplia de geometrías de lentes que en una sola lente. Al igual que una fuente cáustica de una sola lente, la fuente tarda un tiempo finito en cruzar la cáustica. Si se puede medir este tiempo de cruce cáustico y se conoce el radio angular de la fuente, se puede determinar nuevamente el ángulo de Einstein. ^{[ cita requerida ]} ${\displaystyle t_{S}}$

Al igual que en el caso de una sola lente, cuando el aumento de la fuente es formalmente infinito, las lentes binarias cruzadas cáusticas magnificarán diferentes partes de la estrella fuente en diferentes momentos. De este modo, pueden investigar la estructura de la fuente y el oscurecimiento de su borde. ^{[ cita requerida ]}

Eventos que dieron lugar a la paralaje de Einstein

En principio, la paralaje de Einstein se puede medir haciendo que dos observadores observen simultáneamente el evento desde diferentes ubicaciones, por ejemplo, desde la Tierra y desde una nave espacial distante. ^[45] La diferencia en la amplificación observada por los dos observadores produce el componente perpendicular al movimiento de la lente, mientras que la diferencia en el tiempo de amplificación máxima produce el componente paralelo al movimiento de la lente. Esta medición directa se ha informado ^[46] utilizando el telescopio espacial Spitzer . En casos extremos, las diferencias pueden incluso ser medibles a partir de pequeñas diferencias vistas desde telescopios en diferentes ubicaciones de la Tierra, es decir, la paralaje terrestre. ^[47] ${\displaystyle {\vec {\pi }}_{E}}$

La paralaje de Einstein también se puede medir a través de la paralaje orbital; el movimiento del observador, causado por la rotación de la Tierra alrededor del Sol y del Sol a través de la Galaxia, significa que se observa un evento de microlente desde diferentes ángulos en cada época de observación. Esto se informó por primera vez en 1995 ^[48] y se ha informado en un puñado de eventos desde entonces. La paralaje, en eventos de lentes puntuales, se puede medir mejor para eventos de escala de tiempo larga, con un gran , es decir, desde lentes de movimiento lento y baja masa, que están cerca del observador. ${\displaystyle \pi _{E}}$

Si la estrella fuente es una estrella binaria , también tendrá un movimiento relativo adicional, que también puede causar cambios detectables en la curva de luz. Este efecto se conoce como Xallarap (paralaje escrito al revés).

Detección de planetas extrasolares

Microlente gravitacional de un planeta extrasolar

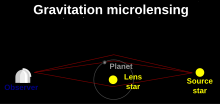
Si el objeto que produce el efecto lente es una estrella con un planeta orbitando alrededor de ella, se trata de un ejemplo extremo de un evento de lente binaria. Si la fuente cruza una cáustica, las desviaciones con respecto a un evento estándar pueden ser grandes incluso para planetas de baja masa. Estas desviaciones nos permiten inferir la existencia y determinar la masa y la separación del planeta alrededor de la lente. Las desviaciones suelen durar unas horas o unos días. Debido a que la señal es más fuerte cuando el evento en sí es más fuerte, los eventos de gran aumento son los candidatos más prometedores para un estudio detallado. Por lo general, un equipo de investigación notifica a la comunidad cuando descubre un evento de gran aumento en curso. Luego, los grupos de seguimiento monitorean intensivamente el evento en curso, con la esperanza de obtener una buena cobertura de la desviación si ocurre. Cuando el evento termina, la curva de luz se compara con modelos teóricos para encontrar los parámetros físicos del sistema. Los parámetros que se pueden determinar directamente a partir de esta comparación son la relación de masa del planeta con la estrella y la relación de la separación angular entre la estrella y el planeta con el ángulo de Einstein. A partir de estas proporciones, junto con suposiciones sobre la estrella lente, se puede estimar la masa del planeta y su distancia orbital. ^{[ cita requerida ]}

Exoplanetas descubiertos mediante microlente, por año, hasta 2014.

El primer éxito de esta técnica lo lograron en 2003 tanto OGLE como MOA del evento de microlente OGLE 2003–BLG–235 (o MOA 2003–BLG–53) . Combinando sus datos, encontraron que la masa planetaria más probable era 1,5 veces la masa de Júpiter. ^[49] Hasta abril de 2020, se han detectado 89 exoplanetas mediante este método. ^[50] Algunos ejemplos notables incluyen OGLE-2005-BLG-071Lb , ^[51] OGLE-2005-BLG-390Lb , ^[52] OGLE-2005-BLG-169Lb , ^[53] dos exoplanetas alrededor de OGLE-2006-BLG-109L , ^[54] y MOA-2007-BLG-192Lb . ^[55] Cabe destacar que, en el momento de su anuncio en enero de 2006, el planeta OGLE-2005-BLG-390Lb probablemente tenía la masa más baja de cualquier exoplaneta conocido que orbitara una estrella regular, con una mediana de 5,5 veces la masa de la Tierra y una incertidumbre de aproximadamente un factor dos. Este récord fue cuestionado en 2007 por Gliese 581 c con una masa mínima de 5 masas terrestres, y desde 2009 Gliese 581 e es el exoplaneta "regular" más ligero conocido, con un mínimo de 1,9 masas terrestres. En octubre de 2017, se informó sobre OGLE-2016-BLG-1190Lb , un exoplaneta extremadamente masivo (o posiblemente una enana marrón ), aproximadamente 13,4 veces la masa de Júpiter . ^[56]

Al comparar este método de detección de planetas extrasolares con otras técnicas, como el método de tránsito , una ventaja es que la intensidad de la desviación planetaria no depende de la masa del planeta con tanta fuerza como lo hacen los efectos en otras técnicas. Esto hace que la microlente sea muy adecuada para encontrar planetas de baja masa. También permite la detección de planetas más alejados de la estrella anfitriona que la mayoría de los otros métodos. Una desventaja es que el seguimiento del sistema de lentes es muy difícil una vez que el evento ha terminado, porque lleva mucho tiempo que la lente y la fuente estén lo suficientemente separadas para resolverlos por separado.

Una lente atmosférica terrestre propuesta por Yu Wang en 1998 que utilizaría la atmósfera de la Tierra como una lente grande también podría obtener imágenes directas de exoplanetas cercanos potencialmente habitables. ^[57]

Experimentos de microlente

Existen dos tipos básicos de experimentos de microlente. Los grupos de "búsqueda" utilizan imágenes de campo amplio para encontrar nuevos eventos de microlente. Los grupos de "seguimiento" a menudo coordinan telescopios en todo el mundo para proporcionar una cobertura intensiva de eventos seleccionados. Los experimentos iniciales tenían todos nombres un tanto atrevidos hasta la formación del grupo PLANET. Actualmente existen propuestas para construir nuevos satélites especializados en microlente o para utilizar otros satélites para estudiar la microlente. ^{[ cita requerida ]}

Buscar colaboraciones

• Alard; Mao; Guibert (1995). "Objeto DUO 2: Un nuevo candidato a lente binaria". Astronomía y astrofísica . 300 : L17. arXiv : astro-ph/9506101 . Código Bibliográfico :1995A&A...300L..17A.Búsqueda de placa fotográfica de bulto.
• Experience de Recherche des Objets Sombres (EROS) (1993–2002) Colaboración principalmente francesa. EROS1: Búsqueda de placas fotográficas de LMC: EROS2: Búsqueda CCD de LMC, SMC, Bulge y brazos espirales.
• MACHO (1993–1999) Colaboración entre Australia y EE. UU. Búsqueda CCD del bulbo y la LMC.
• Experimento de lente gravitacional óptica (OGLE) (1992 – ), colaboración polaca establecida por Paczynski y Udalski . Telescopio de 1,3 m dedicado en Chile dirigido por la Universidad de Varsovia. Objetivos en el bulbo y las Nubes de Magallanes.
• Observaciones de microlente en astrofísica (MOA) (1998 – ), colaboración entre Japón y Nueva Zelanda. Telescopio de 1,8 m dedicado en Nueva Zelanda. Objetivos en el bulbo y las Nubes de Magallanes.
• SuperMACHO (2001 – ), sucesor de la colaboración MACHO, utilizó el telescopio CTIO de 4 m para estudiar las débiles microlentes de la LMC.

Colaboraciones de seguimiento

• Red de Sondeo de Anomalías de Lente (PLANET) Colaboración multinacional.
• MicroFUN , Red de seguimiento de microlentes
• Búsqueda de planetas mediante microlente (MPS) Archivado el 23 de abril de 1999 en Wayback Machine.
• Red de microlente para la detección de pequeños exoplanetas terrestres, MiNDSTEp
• RoboNet: búsqueda de planetas mediante una red global de telescopios robóticos

Efecto de lente de píxeles en la galaxia de Andrómeda

• MEGA
• ÁGAPE (en francés)
• WeCAPP
• El Proyecto Angstrom
• PLAN Archivado el 22 de julio de 2011 en Wayback Machine.

Experimentos satelitales propuestos

• Telescopio de sondeo de exoplanetas galácticos (GEST) Archivado el 16 de mayo de 2001 en Wayback Machine
• El proyecto SIM Microlensing Key habría utilizado la astrometría de altísima precisión del satélite Space Interferometry Mission para romper la degeneración de la microlente y medir la masa, la distancia y la velocidad de las lentes. Este satélite se pospuso varias veces y finalmente se canceló en 2010.
• El telescopio espacial Nancy Grace Roman , que la NASA está preparando para su lanzamiento a mediados de la década de 2020, incluirá un estudio de microlente junto con varios otros estudios. La demografía de microlente complementará la de las misiones Kepler y TESS , con una mejor sensibilidad a planetas como la Tierra y Marte, que tienen más probabilidades de ser planetas rocosos en la zona habitable de sus soles. ^{[ cita requerida ]}

Véase también

• Lente gravitacional
• OGLE-2019-BLG-0960Lb
• Lente atmosférica terrestre

Referencias

1. Joachim Wambsganss (2006). "Microlente gravitacional". Lente gravitacional: fuerte, débil y micro. Cursos avanzados de Saas-Fee. Vol. 33. Saas-Fee Lectures, Springer-Verlag. págs. 453–540. doi :10.1007/978-3-540-30310-7_4. ISBN 978-3-540-30309-1.S2CID119384147  .​
2. Kochanek, CS (2004). "Interpretación cuantitativa de las curvas de luz de microlente de cuásares". The Astrophysical Journal . 605 (1): 58–77. arXiv : astro-ph/0307422 . Código Bibliográfico :2004ApJ...605...58K. doi :10.1086/382180. S2CID  18391317.
3. Poindexter, Shawn; Morgan, Nicholas; Kochanek, Christopher S. (2008). "La estructura espacial de un disco de acreción". The Astrophysical Journal . 673 (1): 34–38. arXiv : 0707.0003 . Código Bibliográfico :2008ApJ...673...34P. doi :10.1086/524190. S2CID  7699211.
4. Eigenbrod, A.; Courbin, F.; Meylan, G.; Agol, E.; Anguita, T.; Schmidt, RW; Wambsganss, J. (2008). "Variabilidad de la microlente en el cuásar con lente gravitacional QSO 2237+0305 = la cruz de Einstein. II. Perfil de energía del disco de acreción". Astronomía y astrofísica . 490 (3): 933–943. arXiv : 0810.0011 . Código Bibliográfico :2008A&A...490..933E. doi :10.1051/0004-6361:200810729. S2CID  14230245.
5. Mosquera, AM; Muñoz, JA; Mediavilla, E. (2009). "Detección de microlente cromática en Q 2237+0305 A". The Astrophysical Journal . 691 (2): 1292–1299. arXiv : 0810.1626 . Código Bibliográfico :2009ApJ...691.1292M. doi :10.1088/0004-637X/691/2/1292. S2CID  15724872.
6. Floyd, David JE; Bate, NF; Webster, RL (2009). "El disco de acreción en el cuásar SDSS J0924+0219". Monthly Notices of the Royal Astronomical Society . 398 (1): 233–239. arXiv : 0905.2651 . Bibcode :2009MNRAS.398..233F. doi : 10.1111/j.1365-2966.2009.15045.x . S2CID  18381541.
7. Kelly (2018). "Aumento extremo de una estrella individual con un corrimiento al rojo de 1,5 mediante una lente de cúmulo de galaxias". Nature Astronomy . 2 (4): 334–342. arXiv : 1706.10279 . Código Bibliográfico :2018NatAs...2..334K. doi :10.1038/s41550-018-0430-3. S2CID  125826925.
8. Diego (2018). "Materia oscura bajo el microscopio: restringiendo la materia oscura compacta con eventos de cruce cáustico". The Astrophysical Journal . 857 (1): 25–52. arXiv : 1706.10281 . Código Bibliográfico :2018ApJ...857...25D. doi : 10.3847/1538-4357/aab617 . S2CID  55811307.
9. Refsdal, S. (1964). "El efecto de lente gravitacional". Monthly Notices of the Royal Astronomical Society . 128 (4): 295–306. Bibcode :1964MNRAS.128..295R. doi : 10.1093/mnras/128.4.295 .
10. Paczyński, B. (1986). "Microlente gravitacional por el halo galáctico". The Astrophysical Journal . 304 : 1. Bibcode :1986ApJ...304....1P. doi : 10.1086/164140 .
11. Boden, AF; Shao, M.; van Buren, D. (1998). "Observación astrométrica de la microlente gravitacional MACHO". The Astrophysical Journal . 502 (2): 538–549. arXiv : astro-ph/9802179 . Código Bibliográfico :1998ApJ...502..538B. doi :10.1086/305913. S2CID  119367990.
12. Delplancke, F.; Górski, KM; Richichi, A. (2001). "Resolución de eventos de microlente gravitacional con interferometría óptica de línea base larga". Astronomía y Astrofísica . 375 (2): 701–710. arXiv : astro-ph/0108178 . Bibcode :2001A&A...375..701D. doi :10.1051/0004-6361:20010783. S2CID  9243538.
13. Dong, Subo; Mérand, A.; Delplancke-Ströbele, F.; Gould, Andrew; et al. (2019). "Primera resolución de imágenes obtenidas con microlentes". The Astrophysical Journal . 871 (1): 70–80. arXiv : 1809.08243 . Código Bibliográfico :2019ApJ...871...70D. doi : 10.3847/1538-4357/aaeffb . S2CID  119434631.
14. Kailash Sahu; et al. (31 de enero de 2022). "Un agujero negro aislado de masa estelar detectado mediante microlente astrométrica". The Astrophysical Journal . 933 (1): 83. arXiv : 2201.13296 . Código Bibliográfico :2022ApJ...933...83S. doi : 10.3847/1538-4357/ac739e . S2CID  246430448.
15. Bohdan Paczyński (10 de febrero de 1998). "Microlente gravitacional con la misión de interferometría espacial ". Astrophysical Journal . 494 (1). arXiv : astro-ph/9708155 . Bibcode :1998ApJ...494L..23P. doi :10.1086/311153. S2CID  13865408.
16. "Un misterio de la microlente" . Consultado el 7 de octubre de 2015 .
17. Minniti, D.; Contreras Ramos, R.; Alonso-García, J.; Anguita, T.; Catelan, M.; Gran, F.; Motta, V.; Muro, G.; Rojas, K.; Saito, RK (2015). "Observaciones de sondeo VVV de un candidato a agujero negro de masa estelar por microlente en el campo del cúmulo globular NGC 6553". The Astrophysical Journal . 810 (2): L20. arXiv : 1508.06957 . Código Bibliográfico :2015ApJ...810L..20M. doi :10.1088/2041-8205/810/2/l20. S2CID  119212281.
18. "¿Hacen boom? - Gaia - Cosmos". www.cosmos.esa.int . Consultado el 18 de junio de 2022 .
19. Wyrzykowski, Łukasz; Kruszyńska, K.; Rybicki, KA; Hol, B.; ur-Taïbi, I. Lecøe; Mowlavi, N.; Nienartowicz, K.; de Fombelle, G. Jevardat; Rimoldini, L.; Audard, M.; García-Lario, P. (2023). " Versión 3 de datos de Gaia ". Astronomía y Astrofísica . 674 : A23. arXiv : 2206.06121 . doi :10.1051/0004-6361/202243756. S2CID  249625849.
20. La colaboración MACHO; Alcock; Allsman; Alves; Axelrod; Becker; Bennett; Cook; Dalal (2000). "El proyecto MACHO: resultados de microlente a partir de 5,7 años de observaciones de LMC". Astrophys. J . 542 (1): 281–307. arXiv : astro-ph/0001272 . Código Bibliográfico :2000ApJ...542..281A. doi :10.1086/309512. S2CID  15077430.
21. Alcock; Allsman; Alves; Axelrod; Becker; Bennett; Cook; Drake; Freeman (2000). "El proyecto MACHO: Microlente óptica de profundidad hacia el bulbo galáctico a partir del análisis de imágenes diferenciales". The Astrophysical Journal . 541 (2): 734–766. arXiv : astro-ph/0002510 . Código Bibliográfico :2000ApJ...541..734A. doi :10.1086/309484. S2CID  119339265.
22. Schneider, Ehlers y Falco. Lentes gravitacionales . 1992.
23. Einstein, A. (1936). "Acción de una estrella similar a una lente por la desviación de la luz en el campo gravitatorio". Science . 84 (2188): 506–7. Bibcode :1936Sci....84..506E. doi :10.1126/science.84.2188.506. PMID  17769014.
24. Chang, K.; Refsdal, S. (1979). "Variaciones de flujo de QSO 0957 + 561 A, B y división de la imagen por estrellas cercanas a la trayectoria de la luz". Nature . 282 (5739): 561–564. Bibcode :1979Natur.282..561C. doi :10.1038/282561a0. S2CID  4325497.
25. Young, P. (1 de marzo de 1981). "Q0957+561: efectos de estrellas aleatorias en la lente gravitacional". The Astrophysical Journal . 244 : 756–767. Bibcode :1981ApJ...244..756Y. doi : 10.1086/158752 .
26. Irwin, MJ; Webster, RL; Hewett, PC; Corrigan, RT; Jedrzejewski, RI (diciembre de 1989). "Variaciones fotométricas en el sistema Q2237 + 0305 - Primera detección de un evento de microlente". The Astronomical Journal . 98 : 1989. Bibcode :1989AJ.....98.1989I. doi :10.1086/115272.
27. Nemiroff, Robert J. (junio de 1986). "Lentes gravitacionales aleatorias". Astrofísica y ciencia espacial . 123 (2): 381–387. Código Bibliográfico :1986Ap&SS.123..381N. doi :10.1007/BF00653957. S2CID  122855233.
28. Nemiroff, Robert J. (diciembre de 1987). Predicción y análisis de fenómenos básicos de microlente gravitacional (Tesis). Bibcode :1987PhDT........12N. doi :10.5281/zenodo.33974.
29. Alcock, C.; Akerlof, C.W.; Allsman, RA; Axelrod, TS; Bennett, DP; Chan, S.; Cook, K.H.; Freeman, K.C.; Griest, K.; Marshall, SL; Park, HS.; Perlmutter, S.; Peterson, BA; Pratt, MR; Quinn, P.J.; Rodgers, A.W.; Stubbs, C.W.; Sutherland, W. (14 de octubre de 1993). "Posible microlente gravitacional de una estrella en la Gran Nube de Magallanes". Nature . 365 (6447): 621–623. arXiv : astro-ph/9309052 . Código Bibliográfico :1993Natur.365..621A. doi :10.1038/365621a0. S2CID  4233746.
30. Aubourg, E.; Bareyre, P.; Bréhin, S.; Gros, M.; Lachièze-Rey, M.; Laurent, B.; Lesquoy, E.; Magneville, C.; Milsztajn, A.; Moscoso, L.; Queennec, F.; Rico, J.; Spiro, M.; Vigroux, L.; Zylberajch, S.; Ansari, R.; Caballero, F.; Moniez, M.; Beaulieu, J.-P.; Ferlet, R.; Grisón, Ph.; Vidal-Madjar, A.; Guibert, J.; Moreau, O.; Tajahmady, F.; Mauricio, E.; Prevôt, L.; Gry, C. (14 de octubre de 1993). "Evidencia de microlente gravitacional por objetos oscuros en el halo galáctico". Naturaleza . 365 (6447): 623–625. Código Bib :1993Natur.365..623A. doi :10.1038/365623a0. S2CID  4303500.
31. Alcock, C.; Allsman, RA; Alves, DR; Axelrod, TS; Becker, AC; Bennett, DP; Cook, KH; Dalal, N.; Drake, AJ; Freeman, KC; Geha, M.; Griest, K.; Lehner, MJ; Marshall, SL; Minniti, D.; Nelson, CA; Peterson, BA; Popowski, P.; Pratt, MR; Quinn, PJ; Stubbs, CW; Sutherland, W.; Tomaney, AB; Vandehei, T.; Welch, D. (10 de octubre de 2000). "El proyecto MACHO: resultados de microlente a partir de 5,7 años de observaciones de la Gran Nube de Magallanes". The Astrophysical Journal . 542 (1): 281–307. arXiv : astro-ph/0001272 . Código bibliográfico : 2000ApJ...542..281A. doi :10.1086/309512. S2CID  15077430.
32. Tisserand, P.; Le Guillou, L.; Alfonso, C.; Alberto, JN; Andersen, J.; Ansari, R.; Aubourg, é.; Bareyre, P.; Beaulieu, JP; Charlot, X.; Costuras, C.; Ferlet, R.; Fouqué, P.; Glicenstein, JF; Goldman, B.; Gould, A.; Graff, D.; Gros, M.; Haissinski, J.; Hamadache, C.; de Kat, J.; Lasserre, T.; Lesquoy, é.; Loup, C.; Magneville, C.; Marquette, JB; Mauricio, é.; Maury, A.; Milsztajn, A.; Moniez, M.; Palanque-Delabrouille, N.; Perdereau, O.; Rahal, YR; Rico, J.; Spiro, M.; Vidal-Madjar, A.; Vigroux, L. (julio de 2007). "Límites del contenido de Macho del halo galáctico del sondeo EROS-2 de las Nubes de Magallanes". Astronomía y Astrofísica . 469 (2): 387–404 . arXiv : astro-ph/0607207 . Código Bibliográfico :2007A&A...469..387T. doi :10.1051/0004-6361:20066017. S2CID  15389106.
33. Observaciones de microlente en astrofísica
34. "Pensando en el futuro". MiNDSTEp .
35. RoboNet
36. Red de seguimiento de microlente
37. Colaboración μFUN-PLANET
38. Gough, Evan (1 de octubre de 2020). «Se ha descubierto un planeta con una masa similar a la de la Tierra flotando libremente en la Vía Láctea sin una estrella». Universe Today . Consultado el 2 de octubre de 2020 .
39. Mroz, Przemek; et al. (29 de septiembre de 2020). "Un candidato a planeta rebelde de masa terrestre detectado en el evento de microlente de escala de tiempo más corta". The Astrophysical Journal . 903 (1): L11. arXiv : 2009.12377 . Bibcode :2020ApJ...903L..11M. doi : 10.3847/2041-8213/abbfad . S2CID  221971000.
40. Gould, Andrew (2000). "Un formalismo natural para la microlente". The Astrophysical Journal . 542 (2): 785–788. arXiv : astro-ph/0001421 . Código Bibliográfico :2000ApJ...542..785G. doi :10.1086/317037. S2CID  15356294.
41. "(sqrt(4*G*60 masas de Júpiter*4000 parsecs/(c^2*4000 parsecs * 8000 parsecs)) radianes) en segundos de arco". Wolframalpha .
42. "1,17 * 10 ^ -9 * 4000 pársecs en au". Wolframalfa .
43. "Microlente" (PDF) . Enciclopedia de Astronomía y Astrofísica . Consultado el 13 de febrero de 2018 .
44. Landis, Geoffrey A. (2017). "Misión al foco gravitacional del Sol: un análisis crítico". 55.ª Reunión de Ciencias Aeroespaciales de la AIAA . arXiv : 1604.06351 . doi :10.2514/6.2017-1679. ISBN 978-1-62410-447-3.
45. Gould, Andrew (1994). "Velocidades MACHO a partir de paralajes basados ​​en satélites". The Astrophysical Journal . 421 : L75. Código Bibliográfico :1994ApJ...421L..75G. doi :10.1086/187191.
46. Dong, Subo; Udalski, A.; Gould, A.; Reach, WT; Christie, GW; Boden, AF; Bennett, DP; Fazio, G.; Griest, K. (2007). "Primera medición de paralaje de microlente basada en el espacio: observaciones de Spitzer de OGLE-2005-SMC-001". The Astrophysical Journal . 664 (2): 862–878. arXiv : astro-ph/0702240 . Código Bibliográfico :2007ApJ...664..862D. doi :10.1086/518536. S2CID  8479357.
47. Hardy, SJ; Walker, MA (1995). "Efectos de paralaje en eventos de microlente binaria". Monthly Notices of the Royal Astronomical Society . 276 (4): L79. Bibcode :1995MNRAS.276L..79H. doi : 10.1093/mnras/276.1.L79 .
48. Alcock, C.; Allsman, RA; Alves, D.; Axelrod, TS; Bennett, DP; Cook, KH; Freeman, KC; Griest, K.; Guern, J. (1995). "Primera observación de paralaje en un evento de microlente gravitacional". The Astrophysical Journal . 454 (2): L125. arXiv : astro-ph/9506114 . Código Bibliográfico :1995ApJ...454L.125A. doi :10.1086/309783. S2CID  119035972.
49. Vínculo; Udalski; Jaroszyński; Rattenbury; Paczyński; Soszynski; Wyrzykowski; Szymanski; Kubiak (2004). "OGLE 2003-BLG-235/MOA 2003-BLG-53: un evento de microlente planetaria". Astrofia. J.​ 606 (2): L155-L158. arXiv : astro-ph/0404309 . Código Bib : 2004ApJ...606L.155B. doi :10.1086/420928. S2CID  17610640.
50. [1] Estadísticas de exoplanetas y candidatos, a través del Archivo de Exoplanetas del Instituto de Ciencia de Exoplanetas de la NASA.
51. Udalski; Jaroszynski; Paczynski; Kubiak; Szymanski; Soszynski; Pietrzynski; Ulaczyk; Szewczyk (2005). "Un planeta de masa joviana en el evento de microlente OGLE-2005-BLG-071". The Astrophysical Journal . 628 (2): L109–L112. arXiv : astro-ph/0505451 . Código Bibliográfico :2005ApJ...628L.109U. doi :10.1086/432795. S2CID  7425167.
52. Sitio web de OGLE Archivado el 5 de junio de 2011 en Wayback Machine.
53. Gould; Udalski; An; Bennett; Zhou; Dong; Rattenbury; Gaudi; Yock (2006). "La microlente OGLE-2005-BLG-169 implica que los planetas fríos similares a Neptuno son comunes". Astrophys. J . 644 (1): L37–L40. arXiv : astro-ph/0603276 . Código Bibliográfico :2006ApJ...644L..37G. doi :10.1086/505421. S2CID  14270439.
54. Gaudí; Bennett; Udalski; Gould; Christie; Maoz; Dong; McCormick; Szymanski (2008). "Descubrimiento de un análogo de Júpiter/Saturno con microlente gravitacional". Science . 319 (5865): 927–930. arXiv : 0802.1920 . Bibcode :2008Sci...319..927G. doi :10.1126/science.1151947. PMID  18276883. S2CID  119281787.
55. Paul Rincon, Hallan el planeta extrasolar más pequeño, BBC, 2 de junio de 2008
56. Ryu, Y.-H.; et al. (27 de octubre de 2017). "OGLE-2016-BLG-1190Lb: el primer planeta del bulbo de Spitzer se encuentra cerca del límite entre planeta y enana marrón". The Astronomical Journal . 155 : 40. arXiv : 1710.09974 . doi : 10.3847/1538-3881/aa9be4 . S2CID  54706921.
57. Wang, Yu (1998). "Telescopio espacial de muy alta resolución que utiliza la atmósfera terrestre como lente objetivo". En Bely, Pierre Y.; Breckinridge, James B. (eds.). Space Telescopes and Instruments V. Vol. 3356. pág. 665. doi :10.1117/12.324434.

Enlaces externos

• Descubren un planeta cinco veces más masivo que la Tierra que orbita una estrella a 20.000 años luz de distancia
• Efecto de lente gravitacional (animación): lente de masa puntual binaria en YouTube