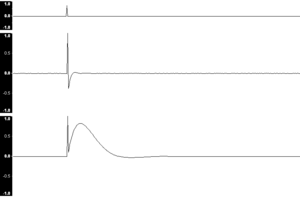
En la teoría de control y procesamiento de señales , la respuesta al impulso , o función de respuesta al impulso ( FRI ), de un sistema dinámico es su salida cuando se le presenta una breve señal de entrada, llamada impulso ( δ( t ) ). De manera más general, una respuesta al impulso es la reacción de cualquier sistema dinámico en respuesta a algún cambio externo. En ambos casos, la respuesta al impulso describe la reacción del sistema como una función del tiempo (o posiblemente como una función de alguna otra variable independiente que parametriza el comportamiento dinámico del sistema).
En todos estos casos, el sistema dinámico y su respuesta al impulso pueden ser objetos físicos reales o pueden ser sistemas matemáticos de ecuaciones que describen dichos objetos.
Dado que la función de impulso contiene todas las frecuencias (véase la transformada de Fourier de la función delta de Dirac , que muestra el ancho de banda de frecuencia infinito que tiene la función delta de Dirac), la respuesta al impulso define la respuesta de un sistema lineal invariante en el tiempo para todas las frecuencias.

Matemáticamente, la descripción del impulso depende de si el sistema se modela en tiempo discreto o continuo . El impulso se puede modelar como una función delta de Dirac para sistemas de tiempo continuo , o como la función de muestra unitaria discreta para sistemas de tiempo discreto . La delta de Dirac representa el caso límite de un pulso que se hace muy corto en el tiempo mientras que mantiene su área o integral (dando así un pico infinitamente alto). Si bien esto es imposible en cualquier sistema real, es una idealización útil. En la teoría del análisis de Fourier , un impulso de este tipo comprende porciones iguales de todas las frecuencias de excitación posibles, lo que lo convierte en una sonda de prueba conveniente.
Cualquier sistema de una clase grande conocida como lineal, invariante en el tiempo ( LTI ) se caracteriza completamente por su respuesta al impulso. Es decir, para cualquier entrada, la salida se puede calcular en términos de la entrada y la respuesta al impulso. (Véase la teoría de sistemas LTI ). La respuesta al impulso de una transformación lineal es la imagen de la función delta de Dirac bajo la transformación, análoga a la solución fundamental de un operador diferencial parcial .
Generalmente es más fácil analizar sistemas utilizando funciones de transferencia en lugar de respuestas al impulso. La función de transferencia es la transformada de Laplace de la respuesta al impulso. La transformada de Laplace de la salida de un sistema puede determinarse mediante la multiplicación de la función de transferencia por la transformada de Laplace de la entrada en el plano complejo , también conocido como dominio de la frecuencia . Una transformada de Laplace inversa de este resultado dará como resultado la salida en el dominio del tiempo .
Para determinar una salida directamente en el dominio del tiempo se requiere la convolución de la entrada con la respuesta al impulso. Cuando se conocen la función de transferencia y la transformada de Laplace de la entrada, esta convolución puede ser más complicada que la alternativa de multiplicar dos funciones en el dominio de la frecuencia .
La respuesta al impulso, considerada como una función de Green , puede considerarse como una "función de influencia": cómo un punto de entrada influye en la salida.
En los sistemas prácticos, no es posible producir un impulso perfecto que sirva como entrada para la prueba; por lo tanto, a veces se utiliza un pulso breve como aproximación de un impulso. Siempre que el pulso sea lo suficientemente corto en comparación con la respuesta al impulso, el resultado será cercano a la respuesta al impulso teórica verdadera. Sin embargo, en muchos sistemas, el accionamiento con un pulso fuerte muy corto puede hacer que el sistema entre en un régimen no lineal, por lo que en su lugar se acciona el sistema con una secuencia pseudoaleatoria y la respuesta al impulso se calcula a partir de las señales de entrada y salida. [1]
Una aplicación que demuestra esta idea fue el desarrollo de la prueba de respuesta de impulso de altavoces en la década de 1970. Los altavoces sufren de inexactitud de fase, un defecto a diferencia de otras propiedades medidas como la respuesta de frecuencia . La inexactitud de fase es causada por frecuencias/octavas (ligeramente) retrasadas que son principalmente el resultado de cruces pasivos (especialmente filtros de orden superior) pero también son causadas por resonancia, almacenamiento de energía en el cono, el volumen interno o los paneles del gabinete que vibran. [2] La medición de la respuesta de impulso, que es un gráfico directo de esta "difuminación temporal", proporcionó una herramienta para usar en la reducción de resonancias mediante el uso de materiales mejorados para conos y gabinetes, así como cambios en el cruce de altavoces. La necesidad de limitar la amplitud de entrada para mantener la linealidad del sistema condujo al uso de entradas como secuencias de longitud máxima pseudoaleatorias y al uso de procesamiento informático para derivar la respuesta de impulso. [3]
El análisis de la respuesta al impulso es una faceta importante del radar , la obtención de imágenes por ultrasonidos y muchas áreas del procesamiento de señales digitales . Un ejemplo interesante serían las conexiones a Internet de banda ancha . Los servicios DSL/de banda ancha utilizan técnicas de ecualización adaptativa para ayudar a compensar la distorsión de la señal y la interferencia introducidas por las líneas telefónicas de cobre que se utilizan para brindar el servicio.
En teoría de control, la respuesta al impulso es la respuesta de un sistema a una entrada delta de Dirac . Esto resulta útil en el análisis de sistemas dinámicos ; la transformada de Laplace de la función delta es 1, por lo que la respuesta al impulso es equivalente a la transformada de Laplace inversa de la función de transferencia del sistema .
En aplicaciones acústicas y de audio, las respuestas de impulso permiten capturar las características acústicas de un lugar, como una sala de conciertos. Hay varios paquetes disponibles que contienen respuestas de impulso de lugares específicos, que van desde salas pequeñas hasta grandes salas de conciertos. Estas respuestas de impulso se pueden utilizar en aplicaciones de reverberación por convolución para permitir que las características acústicas de un lugar en particular se apliquen al audio de destino. [4]
En el procesamiento de señales de guitarra eléctrica y el modelado de amplificadores , el software de modelado suele utilizar grabaciones de respuesta de impulso para recrear el tono grabado de los altavoces de la guitarra.
En economía , y especialmente en el modelado macroeconómico contemporáneo , las funciones de respuesta al impulso se utilizan para describir cómo reacciona la economía a lo largo del tiempo a los impulsos exógenos , que los economistas suelen llamar shocks , y a menudo se modelan en el contexto de una autorregresión vectorial . Los impulsos que a menudo se tratan como exógenos desde un punto de vista macroeconómico incluyen cambios en el gasto público , las tasas impositivas y otros parámetros de política fiscal ; cambios en la base monetaria u otros parámetros de política monetaria ; cambios en la productividad u otros parámetros tecnológicos ; y cambios en las preferencias , como el grado de impaciencia . Las funciones de respuesta al impulso describen la reacción de variables macroeconómicas endógenas como la producción , el consumo , la inversión y el empleo en el momento del shock y en puntos posteriores en el tiempo. [5] [6] Recientemente, se han sugerido en la literatura funciones de respuesta al impulso asimétricas que separan el impacto de un shock positivo de uno negativo. [7]