Material fermiónico pesado

Compuesto intermetálico con electrones 4f y 5f en bandas electrónicas no llenas

En la ciencia de los materiales , los materiales fermiónicos pesados ​​son un tipo específico de compuesto intermetálico , que contiene elementos con electrones 4f o 5f en bandas de electrones no llenas . ^[1] Los electrones son un tipo de fermión , y cuando se encuentran en tales materiales, a veces se los denomina electrones pesados . ^{[2] Los materiales fermiónicos pesados ​​tienen un} calor específico de baja temperatura cuyo término lineal es hasta 1000 veces mayor que el valor esperado del modelo de electrones libres . Las propiedades de los compuestos fermiónicos pesados ​​a menudo derivan de los orbitales f parcialmente llenos de iones de tierras raras o actínidos , que se comportan como momentos magnéticos localizados .

El nombre "fermión pesado" proviene del hecho de que el fermión se comporta como si tuviera una masa efectiva mayor que su masa en reposo. En el caso de los electrones, por debajo de una temperatura característica (típicamente 10 K), los electrones de conducción en estos compuestos metálicos se comportan como si tuvieran una masa efectiva hasta 1000 veces la masa de la partícula libre . Esta gran masa efectiva también se refleja en una gran contribución a la resistividad de la dispersión electrón-electrón a través de la relación Kadowaki-Woods . El comportamiento del fermión pesado se ha encontrado en una amplia variedad de estados, incluidos los estados metálicos, superconductores , aislantes y magnéticos. Ejemplos característicos son CeCu ₆ , CeAl ₃ , CeCu ₂ Si ₂ , YbAl ₃ , UBe ₁₃ y UPt ₃ .

Panorama histórico

El comportamiento de los fermiones pesados ​​fue descubierto por K. Andres, JE Graebner y HR Ott en 1975, quienes observaron enormes magnitudes de la capacidad calorífica específica lineal en CeAl ₃ . ^[3]

Si bien las investigaciones sobre superconductores dopados llevaron a la conclusión de que la existencia de momentos magnéticos localizados y la superconductividad en un material eran incompatibles, se demostró lo contrario cuando en 1979 Frank Steglich et al. descubrieron la superconductividad de fermiones pesados ​​en el material CeCu ₂ Si ₂ . ^[4]

En 1994, el descubrimiento de un punto crítico cuántico y un comportamiento de líquido no fermiónico en el diagrama de fases de compuestos fermiónicos pesados ​​por H. von Löhneysen et al. condujo a un nuevo aumento del interés en la investigación de estos compuestos. ^[5] Otro avance experimental fue la demostración en 1998 (por el grupo de Gil Lonzarich ) de que la criticidad cuántica en fermiones pesados ​​puede ser la razón de la superconductividad no convencional. ^[6]

Los materiales fermiónicos pesados ​​desempeñan un papel importante en la investigación científica actual, actuando como materiales prototípicos para la superconductividad no convencional , el comportamiento de líquido no fermiónico y la criticidad cuántica. La interacción real entre los momentos magnéticos localizados y los electrones de conducción en compuestos fermiónicos pesados ​​aún no se comprende por completo y es un tema de investigación en curso. ^{[ cita requerida ]}

Propiedades

Los materiales fermiónicos pesados ​​pertenecen al grupo de sistemas electrónicos fuertemente correlacionados .

Varios miembros del grupo de materiales fermiónicos pesados ​​se vuelven superconductores por debajo de una temperatura crítica. La superconductividad es poco convencional , es decir, no está contemplada en la teoría BCS .

A altas temperaturas, los compuestos fermiónicos pesados ​​se comportan como metales normales y los electrones pueden describirse como un gas de Fermi , en el que se supone que los electrones son fermiones que no interactúan. En este caso, la interacción entre los electrones f  , que presentan un momento magnético local y los electrones de conducción, puede despreciarse.

La teoría del líquido de Fermi de Lev Landau proporciona un buen modelo para describir las propiedades de la mayoría de los materiales fermiónicos pesados ​​a bajas temperaturas. En esta teoría, los electrones se describen mediante cuasipartículas , que tienen los mismos números cuánticos y carga, pero se tiene en cuenta la interacción de los electrones introduciendo una masa efectiva , que difiere de la masa real de un electrón libre.

Propiedades ópticas

Conductividad óptica típica dependiente de la frecuencia de un compuesto fermiónico pesado. Línea azul: T > T _coh . Línea roja: T < T _coh .

Para obtener las propiedades ópticas de los sistemas de fermiones pesados, estos materiales se han investigado mediante mediciones de espectroscopia óptica . ^[7] En estos experimentos, la muestra se irradia con ondas electromagnéticas con una longitud de onda ajustable . La medición de la luz reflejada o transmitida revela las energías características de la muestra.

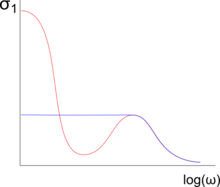
Por encima de la temperatura de coherencia característica , los materiales fermiónicos pesados ​​se comportan como metales normales; es decir, su respuesta óptica se describe mediante el modelo de Drude . Sin embargo, en comparación con un buen metal, los compuestos fermiónicos pesados ​​a altas temperaturas tienen una alta tasa de dispersión debido a la gran densidad de momentos magnéticos locales (al menos un electrón f por celda unitaria), que causan dispersión de Kondo (incoherente) . Debido a la alta tasa de dispersión, la conductividad para CC y a bajas frecuencias es bastante baja. Se produce una caída de conductividad (caída de Drude) en la frecuencia que corresponde a la tasa de relajación. ${\displaystyle T_{\rm {coh}}}$

Abajo , los electrones f localizados  se hibridan con los electrones de conducción. Esto conduce a una mayor masa efectiva y se desarrolla una brecha de hibridación. A diferencia de los aislantes Kondo , el potencial químico de los compuestos de fermiones pesados ​​se encuentra dentro de la banda de conducción. Estos cambios conducen a dos características importantes en la respuesta óptica de los fermiones pesados. ^[1] ${\displaystyle T_{\rm {coh}}}$

La conductividad dependiente de la frecuencia de los materiales de fermiones pesados ​​se puede expresar por , que contiene la masa efectiva y la tasa de relajación renormalizada . ^[8] Debido a la gran masa efectiva, el tiempo de relajación renormalizada también se mejora, lo que lleva a una caída de Drude estrecha a frecuencias muy bajas en comparación con los metales normales. ^{[8] [9]} La tasa de relajación de Drude más baja de este tipo observada en fermiones pesados ​​hasta ahora, en el rango bajo de GHz , se encontró en UPd 2 Al 3 . ^[10] ${\displaystyle \sigma (\omega )={\frac {ne^{2}}{m^{*}}}{\frac {\tau ^{*}}{1+\omega ^{2}\tau ^{*2}}}}$ ${\displaystyle m^{*}}$ ${\displaystyle {\frac {1}{\tau ^{*}}}={\frac {m}{m^{*}}}{\frac {1}{\tau }}}$

La característica de tipo gap en la conductividad óptica representa directamente el gap de hibridación, que se abre debido a la interacción de los electrones f localizados y los electrones de conducción. Dado que la conductividad no desaparece por completo, el gap observado es en realidad un pseudogap . ^[11] A frecuencias incluso más altas podemos observar un máximo local en la conductividad óptica debido a las excitaciones interbandas normales. ^[1]

Capacidad calorífica

Calor específico para metales normales

A baja temperatura y para metales normales, el calor específico consiste en el calor específico de los electrones que depende linealmente de la temperatura y del calor específico de las vibraciones de la red cristalina ( fonones ) que depende cúbicamente de la temperatura. ${\displaystyle C_{P}}$ ${\displaystyle C_{P,{\rm {el}}}}$ ${\displaystyle T}$ ${\displaystyle C_{P,{\rm {ph}}}}$

${\displaystyle C_{P}=C_{P,{\rm {el}}}+C_{P,{\rm {ph}}}=\gamma T+\beta T^{3}\ }$

con constantes de proporcionalidad y . ${\displaystyle \beta }$ ${\displaystyle \gamma }$

En el rango de temperatura mencionado anteriormente, la contribución electrónica es la mayor parte del calor específico. En el modelo de electrones libres (un sistema modelo simple que no tiene en cuenta la interacción de electrones) o en los metales que podrían describirse mediante él, el calor específico electrónico viene dado por

${\displaystyle C_{P,{\rm {el}}}=\gamma T={\frac {\pi ^{2}}{2}}{\frac {k_{\rm {B}}}{\epsilon _{\rm {F}}}}nk_{\rm {B}}T}$

con la constante de Boltzmann , la densidad electrónica y la energía de Fermi (la energía más alta de la partícula individual de los estados electrónicos ocupados). La constante de proporcionalidad se llama coeficiente de Sommerfeld. ${\displaystyle k_{\rm {B}}}$ ${\displaystyle n}$ ${\displaystyle \epsilon _{\rm {F}}}$ ${\displaystyle \gamma }$

Relación entre capacidad calorífica y “masa térmica efectiva”

Para los electrones con una relación de dispersión cuadrática (como para el gas de electrones libres), la energía de Fermi ε _F es inversamente proporcional a la masa de la partícula m :

${\displaystyle \epsilon _{\rm {F}}={\frac {\hbar ^{2}k_{\rm {F}}^{2}}{2m}}}$

donde representa el número de onda de Fermi que depende de la densidad electrónica y es el valor absoluto del número de onda del estado electrónico más ocupado. Por lo tanto, debido a que el parámetro de Sommerfeld es inversamente proporcional a , es proporcional a la masa de la partícula y para valores altos de , el metal se comporta como un gas de Fermi en el que los electrones de conducción tienen una masa térmica efectiva alta. ${\displaystyle k_{\rm {F}}}$ ${\displaystyle \gamma }$ ${\displaystyle \epsilon _{\rm {F}}}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$

Ejemplo: UBe13a bajas temperaturas

Los resultados experimentales para el calor específico del compuesto fermiónico pesado UBe ₁₃ muestran un pico a una temperatura de alrededor de 0,75 K que desciende hasta cero con una pendiente alta si la temperatura se acerca a 0 K. Debido a este pico, el factor es mucho más alto que el modelo de electrones libres en este rango de temperatura. En cambio, por encima de 6 K, el calor específico para este compuesto fermiónico pesado se acerca al valor esperado de la teoría de electrones libres. ${\displaystyle \gamma }$

Criticidad cuántica

La presencia de un momento local y de electrones de conducción deslocalizados conduce a una competencia entre la interacción de Kondo (que favorece un estado fundamental no magnético) y la interacción RKKY (que genera estados ordenados magnéticamente, típicamente antiferromagnéticos para fermiones pesados). Al suprimir la temperatura de Néel de un antiferromagnético de fermiones pesados ​​hasta cero (por ejemplo, aplicando presión o campo magnético o cambiando la composición del material), se puede inducir una transición de fase cuántica . ^[12] Para varios materiales de fermiones pesados ​​se demostró que dicha transición de fase cuántica puede generar propiedades de líquido no fermiónico muy pronunciadas a temperaturas finitas. Este comportamiento crítico cuántico también se estudia en gran detalle en el contexto de la superconductividad no convencional .

Ejemplos de materiales con fermiones pesados ​​con propiedades críticas cuánticas bien estudiadas son CeCu _6−x Au, ^[13] CeIn ₃ , ^[6] CePd ₂ Si ₂ , ^[6] YbRh ₂ Si ₂ y CeCoIn ₅ . ^{[14] [15]}

Algunos compuestos fermiónicos pesados

• CeCoIn ₅
• URu2Si2_​​_​
• UPd2Al3_​​_​
• YbBiPt

Referencias

1. P. Coleman (2007). "Fermiones pesados: electrones en el borde del magnetismo. Manual de magnetismo y materiales magnéticos avanzados". En Helmut Kronmuller; Stuart Parkin (eds.). Manual de magnetismo y materiales magnéticos avanzados . Vol. 1. págs. 95–148. arXiv : cond-mat/0612006 .
2. "Primeras imágenes de electrones pesados ​​en acción". physorg.com. 2 de junio de 2010.
3. K. Andres; JE Graebner; HR Ott (1975). "Formación de 4 f -estado ligado virtual en CeAl ₃ a bajas temperaturas". Physical Review Letters . 35 (26): 1779–1782. Código Bibliográfico :1975PhRvL..35.1779A. doi :10.1103/PhysRevLett.35.1779.
4. Steglich, F.; Aarts, J.; Bredl, CD; Lieke, W.; Meschede, D.; Franz, W.; Schäfer, H. (17 de diciembre de 1979). "Superconductividad en presencia de fuerte paramagnetismo de Pauli: CeCu ₂ Si ₂ ". Cartas de revisión física . 43 (25): 1892–1896. Código bibliográfico : 1979PhRvL..43.1892S. doi : 10.1103/PhysRevLett.43.1892. hdl : 1887/81461 .
5. Löhneysen, H. v.; Pietrus, T.; Portisch, G.; Schlager, HG; Schröder, A.; Sieck, M.; Trappmann, T. (16 de mayo de 1994). "Comportamiento no fermi-líquido en una aleación de fermiones pesados ​​en una inestabilidad magnética". Physical Review Letters . 72 (20): 3262–3265. Bibcode :1994PhRvL..72.3262L. doi :10.1103/PhysRevLett.72.3262. PMID  10056148.
6. Mathur, ND; Grosche, FM; Julian, SR; Walker, IR; Freye, DM; Haselwimmer, RKW; Lonzarich, GG (1998). "Superconductividad mediada magnéticamente en compuestos fermiónicos pesados". Nature . 394 (6688): 39–43. Bibcode :1998Natur.394...39M. doi :10.1038/27838. S2CID  52837444.
7. L. Degiorgi (1999). "La respuesta electrodinámica de compuestos con electrones pesados". Reseñas de Física Moderna . 71 (3): 687–734. Bibcode :1999RvMP...71..687D. doi :10.1103/RevModPhys.71.687.
8. AJ Millis; PA Lee (1987). "Expansión de degeneración de órbitas grandes para el modelo de Anderson en red". Physical Review B . 35 (7): 3394–3414. Bibcode :1987PhRvB..35.3394M. doi :10.1103/PhysRevB.35.3394. PMID  9941843.
9. M. Scheffler; K. Schlegel; C. Clauss; D. Hafner; C. Fella; M. Dressel; M. Jourdan; J. Sichelschmidt; C. Krellner; C. Geibel; F. Steglich (2013). "Espectroscopia de microondas en sistemas de fermiones pesados: sondeo de la dinámica de cargas y momentos magnéticos". Physica Status Solidi B . 250 (3): 439–449. arXiv : 1303.5011 . Código Bibliográfico :2013PSSBR.250..439S. doi :10.1002/pssb.201200925. S2CID  59067473.
10. M. Scheffler; M. Dressel; M. Jourdan; H. Adrian (2005). "Relajación de Drude extremadamente lenta de electrones correlacionados". Nature . 438 (7071): 1135–1137. Bibcode :2005Natur.438.1135S. doi :10.1038/nature04232. PMID  16372004. S2CID  4391917.
11. S. Donovan; A. Schwartz; G. Grüner (1997). "Observación de un pseudogap óptico en UPt ₃ ". Physical Review Letters . 79 (7): 1401–1404. Código Bibliográfico :1997PhRvL..79.1401D. doi :10.1103/PhysRevLett.79.1401.
12. Hilbert v. Löhneysen; et al. (2007). "Inestabilidades del fermi-líquido en transiciones de fase cuánticas magnéticas". Reseñas de Física Moderna . 79 (3): 1015–1075. arXiv : cond-mat/0606317 . Código Bibliográfico :2007RvMP...79.1015L. doi :10.1103/RevModPhys.79.1015. S2CID  119512333.
13. Hv Löhneysen; et al. (1994). "Comportamiento no fermi-líquido en una aleación de fermiones pesados ​​en una inestabilidad magnética". Physical Review Letters . 72 (20): 3262–3265. Bibcode :1994PhRvL..72.3262L. doi :10.1103/PhysRevLett.72.3262. PMID  10056148.
14. J. Paglione; et al. (2003). "Punto crítico cuántico inducido por campo en CeCoIn5". Physical Review Letters . 91 (24): 246405. arXiv : cond-mat/0212502 . Código Bibliográfico :2003PhRvL..91x6405P. doi :10.1103/PhysRevLett.91.246405. PMID  14683139. S2CID  15129138.
15. A. Bianchi; et al. (2003). "Orden antiferromagnético evitado y punto crítico cuántico en CeCoIn5". Physical Review Letters . 91 (25): 257001. arXiv : cond-mat/0302226 . Código Bibliográfico :2003PhRvL..91y7001B. doi :10.1103/PhysRevLett.91.257001. PMID  14754138. S2CID  7562124.

Lectura adicional

• Kittel, Charles (1996) Introducción a la física del estado sólido , 7.ª edición, John Wiley and Sons, Inc.
• Marder, MP (2000), Física de la materia condensada, John Wiley & Sons, Nueva York.
• Hewson, AC (1993), El problema de Kondo para fermiones pesados, Cambridge University Press.
• Fulde, P. (1995), Correlaciones electrónicas en moléculas y sólidos, Springer, Berlín.
• Amusia, M., Popov, K., Shaginyan, V., Stephanovich, V. (2015). Teoría de compuestos de fermiones pesados ​​- Teoría de sistemas de Fermi fuertemente correlacionados . Springer Series in Solid-State Sciences. Vol. 182. Springer. Bibcode :2015thct.book.....A. doi :10.1007/978-3-319-10825-4. ISBN 978-3-319-10824-7.{{cite book}}: CS1 maint: multiple names: authors list (link)