En informática , un algoritmo de búsqueda es un algoritmo diseñado para resolver un problema de búsqueda . Los algoritmos de búsqueda funcionan para recuperar información almacenada dentro de una estructura de datos particular , o calculada en el espacio de búsqueda de un dominio de problema, con valores discretos o continuos .
Aunque los motores de búsqueda utilizan algoritmos de búsqueda, estos pertenecen al estudio de la recuperación de información , no de la algoritmia.
El algoritmo de búsqueda adecuado que se debe utilizar depende a menudo de la estructura de datos que se está buscando y también puede incluir conocimientos previos sobre los datos. Los algoritmos de búsqueda se pueden hacer más rápidos o más eficientes mediante estructuras de bases de datos especialmente construidas, como árboles de búsqueda , mapas hash e índices de bases de datos . [1] [2]
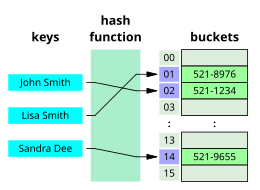
Los algoritmos de búsqueda se pueden clasificar en función de su mecanismo de búsqueda en tres tipos de algoritmos: lineal, binario y hash. Los algoritmos de búsqueda lineal comprueban cada registro en busca del asociado con una clave de destino de forma lineal. [3] Las búsquedas binarias, o de medio intervalo, apuntan repetidamente al centro de la estructura de búsqueda y dividen el espacio de búsqueda por la mitad. Los algoritmos de búsqueda por comparación mejoran la búsqueda lineal al eliminar sucesivamente registros en función de las comparaciones de las claves hasta que se encuentra el registro de destino, y se pueden aplicar en estructuras de datos con un orden definido. [4] Los algoritmos de búsqueda digital funcionan en función de las propiedades de los dígitos en las estructuras de datos mediante el uso de claves numéricas. [5] Finalmente, el hash asigna directamente las claves a los registros en función de una función hash . [6]
Los algoritmos suelen evaluarse por su complejidad computacional o tiempo máximo de ejecución teórico. Las funciones de búsqueda binaria, por ejemplo, tienen una complejidad máxima de O (log n ) o tiempo logarítmico. En términos simples, la cantidad máxima de operaciones necesarias para encontrar el objetivo de búsqueda es una función logarítmica del tamaño del espacio de búsqueda.
Las aplicaciones específicas de los algoritmos de búsqueda incluyen:
Los algoritmos para buscar espacios virtuales se utilizan en el problema de satisfacción de restricciones , donde el objetivo es encontrar un conjunto de asignaciones de valores a ciertas variables que satisfagan ecuaciones matemáticas específicas e inecuaciones /igualdades. También se utilizan cuando el objetivo es encontrar una asignación de variable que maximice o minimice una determinada función de esas variables. Los algoritmos para estos problemas incluyen la búsqueda básica de fuerza bruta (también llamada búsqueda "ingenua" o "desinformada"), y una variedad de heurísticas que intentan explotar el conocimiento parcial sobre la estructura de este espacio, como la relajación lineal, la generación de restricciones y la propagación de restricciones .
Una subclase importante son los métodos de búsqueda local , que ven los elementos del espacio de búsqueda como los vértices de un gráfico, con bordes definidos por un conjunto de heurísticas aplicables al caso; y escanean el espacio moviéndose de un elemento a otro a lo largo de los bordes, por ejemplo de acuerdo con el criterio de descenso más pronunciado o el mejor primero , o en una búsqueda estocástica . Esta categoría incluye una gran variedad de métodos metaheurísticos generales , como el recocido simulado , la búsqueda tabú , los equipos A y la programación genética , que combinan heurísticas arbitrarias de formas específicas. Lo opuesto a la búsqueda local serían los métodos de búsqueda global. Este método es aplicable cuando el espacio de búsqueda no está limitado y todos los aspectos de la red dada están disponibles para la entidad que ejecuta el algoritmo de búsqueda. [7]
Esta clase también incluye varios algoritmos de búsqueda de árboles , que ven los elementos como vértices de un árbol y recorren ese árbol en un orden especial. Ejemplos de estos últimos incluyen los métodos exhaustivos como la búsqueda en profundidad y la búsqueda en amplitud , así como varios métodos de poda de árboles de búsqueda basados en heurísticas como el backtracking y el branch and bound . A diferencia de las metaheurísticas generales, que en el mejor de los casos funcionan solo en un sentido probabilístico, muchos de estos métodos de búsqueda de árboles tienen la garantía de encontrar la solución exacta u óptima, si se les da suficiente tiempo. Esto se llama " completitud ".
Otra subclase importante consiste en algoritmos para explorar el árbol de juego de juegos de varios jugadores, como ajedrez o backgammon , cuyos nodos consisten en todas las posibles situaciones de juego que podrían resultar de la situación actual. El objetivo en estos problemas es encontrar el movimiento que proporcione la mejor posibilidad de victoria, teniendo en cuenta todos los movimientos posibles del oponente o los oponentes. Problemas similares ocurren cuando los humanos o las máquinas tienen que tomar decisiones sucesivas cuyos resultados no están completamente bajo el control de uno, como en la guía de robots o en la planificación de estrategias de marketing , financieras o militares . Este tipo de problema ( búsqueda combinatoria ) se ha estudiado ampliamente en el contexto de la inteligencia artificial . Ejemplos de algoritmos para esta clase son el algoritmo minimax , la poda alfa-beta y el algoritmo A* y sus variantes.
El nombre "búsqueda combinatoria" se utiliza generalmente para algoritmos que buscan una subestructura específica de una estructura discreta dada , como un gráfico, una cadena , un grupo finito , etc. El término optimización combinatoria se utiliza normalmente cuando el objetivo es encontrar una subestructura con un valor máximo (o mínimo) de algún parámetro. (Dado que la subestructura suele estar representada en el ordenador por un conjunto de variables enteras con restricciones, estos problemas pueden considerarse casos especiales de satisfacción de restricciones u optimización discreta; pero normalmente se formulan y resuelven en un entorno más abstracto en el que no se menciona explícitamente la representación interna).
Una subclase importante y ampliamente estudiada son los algoritmos de grafos , en particular los algoritmos de recorrido de grafos , para encontrar subestructuras específicas en un grafo dado, como subgrafos , caminos , circuitos, etc. Algunos ejemplos incluyen el algoritmo de Dijkstra , el algoritmo de Kruskal , el algoritmo del vecino más cercano y el algoritmo de Prim .
Otra subclase importante de esta categoría son los algoritmos de búsqueda de cadenas , que buscan patrones dentro de las cadenas. Dos ejemplos famosos son los algoritmos Boyer-Moore y Knuth-Morris-Pratt , y varios algoritmos basados en la estructura de datos de árbol de sufijos .
En 1953, el estadístico estadounidense Jack Kiefer ideó la búsqueda de Fibonacci , que puede utilizarse para encontrar el máximo de una función unimodal y tiene muchas otras aplicaciones en la informática.
También existen métodos de búsqueda diseñados para ordenadores cuánticos , como el algoritmo de Grover , que teóricamente son más rápidos que la búsqueda lineal o de fuerza bruta incluso sin la ayuda de estructuras de datos o heurísticas. Si bien las ideas y aplicaciones detrás de los ordenadores cuánticos aún son completamente teóricas, se han realizado estudios con algoritmos como el de Grover que replican con precisión las versiones físicas hipotéticas de los sistemas de computación cuántica. [8]
Categorías: