Efecto Doppler relativista

Scientific phenomenon

Figura 1. Una fuente de ondas de luz que se mueve hacia la derecha, en relación con los observadores, con una velocidad de 0,7 c . La frecuencia es mayor para los observadores de la derecha y menor para los de la izquierda.

El efecto Doppler relativista es el cambio en la frecuencia , longitud de onda y amplitud ^[1] de la luz, causado por el movimiento relativo de la fuente y el observador (como en el efecto Doppler clásico ), al tomar en cuenta los efectos descritos por la teoría especial de la relatividad .

El efecto Doppler relativista es diferente del efecto Doppler no relativista porque las ecuaciones incluyen el efecto de dilatación del tiempo de la relatividad especial y no involucran el medio de propagación como punto de referencia. Describen la diferencia total en las frecuencias observadas y poseen la simetría de Lorentz requerida .

Los astrónomos conocen tres fuentes de corrimiento al rojo o al azul : los corrimientos Doppler, los corrimientos al rojo gravitacionales (debidos a la luz que sale de un campo gravitacional) y la expansión cosmológica (donde el propio espacio se estira). Este artículo se ocupa únicamente de los corrimientos Doppler.

Resumen de los principales resultados

En la siguiente tabla se supone que el receptor y la fuente se alejan uno del otro, siendo la velocidad relativa y la velocidad de la luz, y . ${\displaystyle \beta =v/c>0}$ ${\displaystyle v}$ ${\displaystyle c}$ ${\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}$

Derivación

Efecto Doppler longitudinal relativista

El desplazamiento Doppler relativista para el caso longitudinal, con la fuente y el receptor moviéndose directamente uno hacia el otro o alejándose uno del otro, se deriva a menudo como si fuera el fenómeno clásico, pero modificado mediante la adición de un término de dilatación del tiempo . ^{[2] [3]} Este es el enfoque empleado en los libros de texto de física o mecánica de primer año, como los de Feynman ^[4] o Morin. ^[5]

Siguiendo este enfoque para derivar el efecto Doppler longitudinal relativista, supongamos que el receptor y la fuente se alejan uno del otro con una velocidad relativa medida por un observador en el receptor o la fuente (la convención de signos adoptada aquí es que es negativa si el receptor y la fuente se mueven uno hacia el otro). ${\displaystyle v\,}$ ${\displaystyle v\,}$

Consideremos el problema en el marco de referencia de la fuente.

Supongamos que un frente de onda llega al receptor. El siguiente frente de onda se encuentra a una distancia del receptor (donde es la longitud de onda , es la frecuencia de las ondas que emite la fuente y es la velocidad de la luz ). ${\displaystyle \lambda _{s}=c/f_{s}\,}$ ${\displaystyle \lambda _{s}\,}$ ${\displaystyle f_{s}\,}$ ${\displaystyle c\,}$

El frente de onda se mueve con velocidad , pero al mismo tiempo el receptor se aleja con velocidad durante un tiempo , que es el período de las ondas de luz que inciden en el receptor, como se observa en el marco de la fuente. Entonces, donde es la velocidad del receptor en términos de la velocidad de la luz. La correspondiente , la frecuencia de a la que los frentes de onda inciden en el receptor en el marco de la fuente, es: ${\displaystyle c\,}$ ${\displaystyle v}$ ${\displaystyle t_{r,s}}$ $${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$ ${\displaystyle \beta =v/c\,}$ ${\displaystyle f_{r,s}}$ $${\displaystyle f_{r,s}=1/t_{r,s}=f_{s}(1-\beta ).}$$

Hasta ahora, las ecuaciones han sido idénticas a las del efecto Doppler clásico con una fuente estacionaria y un receptor en movimiento.

Sin embargo, debido a los efectos relativistas, los relojes del receptor están dilatados en el tiempo en relación con los relojes de la fuente: , donde es el factor de Lorentz . Para saber qué tiempo está dilatado, recordamos que es el tiempo en el marco en el que la fuente está en reposo. El receptor medirá la frecuencia recibida para ser ${\displaystyle t_{r}=t_{r,s}/\gamma }$ ${\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}$ ${\displaystyle t_{r,s}}$

Ecuación 1:    ${\displaystyle f_{r}=f_{r,s}\gamma }$ ${\displaystyle ={\frac {1-\beta }{\sqrt {1-\beta ^{2}}}}f_{s}}$ ${\displaystyle ={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{s}.}$

La proporción

${\displaystyle {\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}}}$

se denomina factor Doppler de la fuente con respecto al receptor. (Esta terminología es particularmente frecuente en el campo de la astrofísica : véase emisión relativista ).

Las longitudes de onda correspondientes están relacionadas por

Ecuación 2:    ${\displaystyle {\frac {\lambda _{r}}{\lambda _{s}}}={\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}},}$

Expresiones idénticas para el efecto Doppler relativista se obtienen cuando se realiza el análisis en el marco de referencia del receptor con una fuente en movimiento. Esto coincide con las expectativas del principio de relatividad , que dicta que el resultado no puede depender de qué objeto se considera que está en reposo. Por el contrario, el efecto Doppler no relativista clásico depende de si es la fuente o el receptor el que está estacionario con respecto al medio. ^{[4] [5]}

Efecto Doppler transversal

Supongamos que una fuente y un receptor se están aproximando entre sí en un movimiento inercial uniforme a lo largo de trayectorias que no colisionan. El efecto Doppler transversal (TDE) puede referirse a (a) el corrimiento al azul nominal predicho por la relatividad especial que ocurre cuando el emisor y el receptor están en sus puntos de aproximación más cercana; o (b) el corrimiento al rojo nominal predicho por la relatividad especial cuando el receptor ve al emisor como si estuviera en su aproximación más cercana. ^[5] El efecto Doppler transversal es una de las principales predicciones novedosas de la teoría de la relatividad especial.

El hecho de que un informe científico describa el TDE como un corrimiento al rojo o al azul depende de los detalles del experimento en cuestión. Por ejemplo, la descripción original que Einstein hizo del TDE en 1907 describía a un experimentador que observaba el centro (el punto más cercano) de un haz de " rayos canal " (un haz de iones positivos que se crea mediante ciertos tipos de tubos de descarga de gas). Según la relatividad especial, la frecuencia emitida por los iones en movimiento se reduciría en el factor de Lorentz, de modo que la frecuencia recibida se reduciría (se desplazaría al rojo) en el mismo factor. ^{[p 1] [nota 1]}

Por otra parte, Kündig (1963) describió un experimento en el que un absorbedor Mössbauer se hizo girar en una trayectoria circular rápida alrededor de un emisor Mössbauer central. ^{[p 3]} Como se explica a continuación, esta disposición experimental dio como resultado la medición de Kündig de un desplazamiento al azul.

La fuente y el receptor están en sus puntos de aproximación más cercanos.

Figura 2. La fuente y el receptor están en sus puntos de aproximación más cercanos. (a) Análisis en el marco del receptor. (b) Análisis en el marco de la fuente.

En este escenario, el punto de aproximación más cercano es independiente del marco y representa el momento en el que no hay cambios en la distancia en función del tiempo. La figura 2 demuestra que la facilidad de análisis de este escenario depende del marco en el que se analiza. ^[5]

• Fig. 2a. Si analizamos el escenario en el marco del receptor, encontramos que el análisis es más complicado de lo que debería ser. La posición aparente de un objeto celeste está desplazada de su posición verdadera (o posición geométrica) debido al movimiento del objeto durante el tiempo que tarda su luz en llegar a un observador. La fuente estaría dilatada en el tiempo con respecto al receptor, pero el corrimiento al rojo implícito en esta dilatación del tiempo estaría compensado por un corrimiento al azul debido al componente longitudinal del movimiento relativo entre el receptor y la posición aparente de la fuente.
• Fig. 2b. Es mucho más fácil si, en cambio, analizamos el escenario desde el marco de la fuente. Un observador situado en la fuente sabe, a partir del enunciado del problema, que el receptor está en su punto más cercano a él. Eso significa que el receptor no tiene un componente longitudinal de movimiento que complique el análisis. (es decir, dr/dt = 0 donde r es la distancia entre el receptor y la fuente). Dado que los relojes del receptor están dilatados en el tiempo con respecto a la fuente, la luz que recibe el receptor está desplazada hacia el azul por un factor de gamma. En otras palabras,

Ecuación 3:    ${\displaystyle f_{r}=\gamma f_{s}}$

ReceptorveLa fuente como estando en su punto más cercano

Figura 3. Desplazamiento Doppler transversal para el escenario en el que el receptor ve la fuente en su punto más cercano.

Este escenario es equivalente a que el receptor mire en ángulo recto directo a la trayectoria de la fuente. El análisis de este escenario se realiza mejor desde el marco del receptor. La figura 3 muestra el receptor iluminado por la luz del momento en que la fuente estaba más cerca del receptor, aunque la fuente se haya movido. ^[5] Debido a que el reloj de la fuente está dilatado en el tiempo, medido en el marco del receptor, y debido a que no hay un componente longitudinal de su movimiento, la luz de la fuente, emitida desde este punto más cercano, se desplaza hacia el rojo con la frecuencia.

Ecuación 4:    ${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}$

En la literatura, la mayoría de los informes sobre el desplazamiento Doppler transversal analizan el efecto en términos de un receptor apuntando en ángulo recto directo a la trayectoria de la fuente, considerando así la fuente como si estuviera en su punto más cercano y se observara un desplazamiento al rojo.

Punto de desplazamiento de frecuencia nulo

Figura 4. Se produce un cambio de frecuencia nulo para un pulso que recorre la distancia más corta desde la fuente hasta el receptor.

Dado que, en el caso en que la fuente y el receptor que se mueven inercialmente están geométricamente en su aproximación más cercana entre sí, el receptor observa un corrimiento al azul, mientras que en el caso en que el receptor ve que la fuente está en su punto más cercano, el receptor observa un corrimiento al rojo, obviamente debe existir un punto donde el corrimiento al azul cambia a un corrimiento al rojo. En la Fig. 2, la señal viaja perpendicularmente a la trayectoria del receptor y está desplazada al azul. En la Fig. 3, la señal viaja perpendicularmente a la trayectoria de la fuente y está desplazada al rojo.

Como se ve en la figura 4, se produce un desplazamiento nulo de la frecuencia para un pulso que recorre la distancia más corta desde la fuente hasta el receptor. Cuando se observa en el marco donde la fuente y el receptor tienen la misma velocidad, este pulso se emite perpendicularmente a la trayectoria de la fuente y se recibe perpendicularmente a la trayectoria del receptor. El pulso se emite ligeramente antes del punto de aproximación más cercano y se recibe ligeramente después. ^[6]

Un objeto en movimiento circular alrededor de otro.

Figura 5. Efecto Doppler transversal para dos escenarios: (a) receptor moviéndose en un círculo alrededor de la fuente; (b) fuente moviéndose en un círculo alrededor del receptor.

La figura 5 ilustra dos variantes de este escenario. Ambas variantes pueden analizarse utilizando argumentos simples de dilatación del tiempo. ^[5] La figura 5a es esencialmente equivalente al escenario descrito en la figura 2b, y el receptor observa que la luz de la fuente está desplazada hacia el azul por un factor de . La figura 5b es esencialmente equivalente al escenario descrito en la figura 3, y la luz está desplazada hacia el rojo. ${\displaystyle \gamma }$

La única complicación aparente es que los objetos en órbita se encuentran en movimiento acelerado. Una partícula acelerada no tiene un marco inercial en el que siempre esté en reposo. Sin embargo, siempre se puede encontrar un marco inercial que se mueva momentáneamente con la partícula. Este marco, el marco de referencia que se mueve momentáneamente (MCRF) , permite la aplicación de la relatividad especial al análisis de partículas aceleradas. Si un observador inercial mira un reloj que se acelera, solo la velocidad instantánea del reloj es importante para calcular la dilatación del tiempo. ^[7]

Sin embargo, lo contrario no es cierto. El análisis de escenarios en los que ambos objetos se encuentran en movimiento acelerado requiere un análisis algo más sofisticado. No comprender este punto ha dado lugar a confusión y malentendidos.

Fuente y receptor ambos en movimiento circular alrededor de un centro común

Figura 6. La fuente y el receptor están colocados en extremos opuestos de un rotor, equidistantes del centro.

Supongamos que la fuente y el receptor están ubicados en extremos opuestos de un rotor giratorio, como se ilustra en la figura 6. Los argumentos cinemáticos (relatividad especial) y los argumentos basados ​​en observar que no hay diferencia de potencial entre la fuente y el receptor en el campo pseudogravitacional del rotor (relatividad general) conducen a la conclusión de que no debería haber ningún desplazamiento Doppler entre la fuente y el receptor.

En 1961, Champeney y Moon realizaron un experimento con rotor Mössbauer para probar exactamente este escenario y descubrieron que el proceso de absorción de Mössbauer no se veía afectado por la rotación. ^{[p 4]} Concluyeron que sus hallazgos respaldaban la relatividad especial.

Esta conclusión generó cierta controversia. Un cierto crítico persistente de la relatividad ^{[ ¿quién? ]} sostuvo que, aunque el experimento era consistente con la relatividad general, refutaba la relatividad especial, y sostuvo que, dado que el emisor y el absorbedor estaban en movimiento relativo uniforme, la relatividad especial exigía que se observara un desplazamiento Doppler. La falacia del argumento de este crítico era, como se demostró en la sección Punto de desplazamiento de frecuencia nulo, que simplemente no es cierto que siempre deba observarse un desplazamiento Doppler entre dos sistemas en movimiento relativo uniforme. ^[8] Además, como se demostró en la sección Fuente y receptor están en sus puntos de aproximación más cercanos, la dificultad de analizar un escenario relativista a menudo depende de la elección del sistema de referencia. Intentar analizar el escenario en el sistema de referencia del receptor implica mucho álgebra tediosa. Es mucho más fácil, casi trivial, establecer la falta de desplazamiento Doppler entre el emisor y el absorbedor en el sistema de referencia del laboratorio. ^[8]

En realidad, sin embargo, el experimento de Champeney y Moon no decía nada a favor ni en contra de la relatividad especial. Debido a la simetría del montaje, resulta que prácticamente cualquier teoría concebible del desplazamiento Doppler entre sistemas en movimiento inercial uniforme debe arrojar un resultado nulo en este experimento. ^[8]

En lugar de estar equidistantes del centro, supongamos que el emisor y el absorbedor estuvieran a diferentes distancias del centro del rotor. Para un emisor en un radio y un absorbedor en un radio en cualquier parte del rotor, la relación entre la frecuencia del emisor y la frecuencia del absorbedor viene dada por ${\displaystyle R'}$ ${\displaystyle R}$ ${\displaystyle f',}$ ${\displaystyle f,}$

Ecuación 5:    ${\displaystyle {\frac {f'}{f}}=\left({\frac {c^{2}-R^{2}\omega ^{2}}{c^{2}-R'^{2}\omega ^{2}}}\right)^{1/2}}$

donde es la velocidad angular del rotor. La fuente y el emisor no tienen que estar separados por 180°, sino que pueden estar en cualquier ángulo con respecto al centro. ^{[p 5] [9]} ${\displaystyle \omega }$

Movimiento en una dirección arbitraria

Figura 7. Desplazamiento Doppler con la fuente moviéndose en un ángulo arbitrario con respecto a la línea entre la fuente y el receptor.

El análisis utilizado en la sección Efecto Doppler longitudinal relativista se puede ampliar de manera sencilla para calcular el desplazamiento Doppler para el caso en que los movimientos inerciales de la fuente y el receptor se encuentran en cualquier ángulo especificado. ^{[3] [10]} La figura 7 presenta el escenario desde el marco del receptor, con la fuente moviéndose a una velocidad en un ángulo medido en el marco del receptor. El componente radial del movimiento de la fuente a lo largo de la línea de visión es igual a ${\displaystyle v}$ ${\displaystyle \theta _{r}}$ ${\displaystyle v\cos {\theta _{r}}.}$

La siguiente ecuación se puede interpretar como el desplazamiento Doppler clásico para una fuente estacionaria y móvil modificado por el factor de Lorentz. ${\displaystyle \gamma :}$

Ecuación 6:    ${\displaystyle f_{r}={\frac {f_{s}}{\gamma \left(1+\beta \cos \theta _{r}\right)}}.}$

En el caso en que se obtiene el efecto Doppler transversal: ${\displaystyle \theta _{r}=90^{\circ }}$

${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}.\,}$

En su artículo de 1905 sobre la relatividad especial, ^{[p 2]} Einstein obtuvo una ecuación de aspecto algo diferente para la ecuación del desplazamiento Doppler. Después de cambiar los nombres de las variables en la ecuación de Einstein para que sean coherentes con los utilizados aquí, su ecuación se lee así:

Ecuación 7:    ${\displaystyle f_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)f_{s}.}$

Las diferencias se deben al hecho de que Einstein evaluó el ángulo con respecto al sistema de referencia en reposo de la fuente en lugar del sistema de referencia en reposo del receptor. no es igual a debido al efecto de la aberración relativista . La ecuación de la aberración relativista es: ${\displaystyle \theta _{s}}$ ${\displaystyle \theta _{s}}$ ${\displaystyle \theta _{r}}$

Ecuación 8:    ${\displaystyle \cos \theta _{r}={\frac {\cos \theta _{s}-\beta }{1-\beta \cos \theta _{s}}}\,}$

Sustituyendo la ecuación de aberración relativista Ecuación 8 en la Ecuación 6 se obtiene la Ecuación 7 , lo que demuestra la consistencia de estas ecuaciones alternativas para el desplazamiento Doppler. ^[10]

El ajuste en la ecuación 6 o en la ecuación 7 produce la ecuación 1 , la expresión para el desplazamiento Doppler longitudinal relativista. ${\displaystyle \theta _{r}=0}$ ${\displaystyle \theta _{s}=0}$

En Landau y Lifshitz (2005) se puede encontrar un enfoque de cuatro vectores para derivar estos resultados. ^[11]

En las ondas electromagnéticas, tanto las amplitudes del campo eléctrico como del magnético, E y B, se transforman de manera similar a la frecuencia: ^[12]

${\displaystyle E_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)E_{s}}$

${\displaystyle B_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)B_{s}.}$

Visualización

Figura 8. Comparación del efecto Doppler relativista (arriba) con el efecto no relativista (abajo).

La figura 8 nos ayuda a entender, en un sentido cualitativo aproximado, cómo el efecto Doppler relativista y la aberración relativista difieren del efecto Doppler no relativista y la aberración no relativista de la luz . Supongamos que el observador está rodeado uniformemente en todas las direcciones por estrellas amarillas que emiten luz monocromática de 570 nm. Las flechas en cada diagrama representan el vector de velocidad del observador en relación con su entorno, con una magnitud de 0,89  c .

• En el caso relativista, la luz que se encuentra delante del observador se desplaza hacia el azul hasta una longitud de onda de 137 nm en el ultravioleta lejano, mientras que la luz que se encuentra detrás del observador se desplaza hacia el rojo hasta una longitud de onda de 2400 nm en el infrarrojo de longitud de onda corta. Debido a la aberración relativista de la luz, los objetos que antes se encontraban en ángulo recto con el observador parecen desplazados hacia delante 63°.
• En el caso no relativista, la luz que se encuentra delante del observador se desplaza hacia el azul hasta una longitud de onda de 300 nm en el ultravioleta medio, mientras que la luz que se encuentra detrás del observador se desplaza hacia el rojo hasta 5200 nm en el infrarrojo intermedio. Debido a la aberración de la luz, los objetos que antes se encontraban en ángulo recto con el observador aparecen desplazados hacia delante 42°.
• En ambos casos, las estrellas monocromáticas que se encuentran delante y detrás del observador están desplazadas por el efecto Doppler hacia longitudes de onda invisibles. Sin embargo, si el observador tuviera ojos que pudieran ver en el ultravioleta y el infrarrojo, vería las estrellas que se encuentran delante de él más brillantes y más agrupadas que las que se encuentran detrás, pero las estrellas serían mucho más brillantes y mucho más concentradas en el caso relativista. ^[13]

Las estrellas reales no son monocromáticas, sino que emiten una gama de longitudes de onda que se aproximan a la distribución de un cuerpo negro . No es necesariamente cierto que las estrellas que se encuentran frente al observador muestren un color más azul. Esto se debe a que toda la distribución de energía espectral está desplazada. Al mismo tiempo que la luz visible se desplaza hacia el azul, pasando a longitudes de onda ultravioleta invisibles, la luz infrarroja se desplaza hacia el azul, pasando al rango visible. Los cambios precisos en los colores que se observan dependen de la fisiología del ojo humano y de las características espectrales de las fuentes de luz que se observan. ^{[14] [15]}

Efecto Doppler sobre la intensidad

El efecto Doppler (con dirección arbitraria) también modifica la intensidad de la fuente percibida: esto se puede expresar de manera concisa por el hecho de que la intensidad de la fuente dividida por el cubo de la frecuencia es un invariante de Lorentz ^{[pág. 6] [nota 2].} Esto implica que la intensidad radiante total (sumando todas las frecuencias) se multiplica por la cuarta potencia del factor Doppler para la frecuencia.

Como consecuencia, dado que la ley de Planck describe que la radiación del cuerpo negro tiene una intensidad espectral en frecuencia proporcional a (donde es la temperatura de la fuente y la frecuencia), podemos sacar la conclusión de que un espectro de cuerpo negro visto a través de un desplazamiento Doppler (con dirección arbitraria) sigue siendo un espectro de cuerpo negro con una temperatura multiplicada por el mismo factor Doppler que la frecuencia. ${\displaystyle {\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$ ${\displaystyle T}$ ${\displaystyle f}$

Este resultado proporciona una de las pruebas que sirven para distinguir la teoría del Big Bang de las teorías alternativas propuestas para explicar el corrimiento al rojo cosmológico . ^[16]

Verificación experimental

Dado que el efecto Doppler transversal es una de las principales predicciones novedosas de la teoría de la relatividad especial, la detección y cuantificación precisa de este efecto ha sido un objetivo importante de los experimentos que intentan validar la relatividad especial.

Mediciones de tipo Ives y Stilwell

Figura 9. Por qué es difícil medir con precisión el efecto Doppler transversal utilizando un haz transversal.

Einstein (1907) había sugerido inicialmente que la TDE podría medirse observando un haz de " rayos canal " en ángulo recto con el haz. ^{[p 1]} Los intentos de medir la TDE siguiendo este esquema resultaron poco prácticos, ya que la velocidad máxima de un haz de partículas disponible en ese momento era sólo unas pocas milésimas de la velocidad de la luz.

La figura 9 muestra los resultados de intentar medir la línea de 4861 angstroms emitida por un haz de rayos canal (una mezcla de iones H1+, H2+ y H3+) a medida que se recombinan con electrones extraídos del gas hidrógeno diluido utilizado para llenar el tubo de rayos canal. Aquí, el resultado previsto de la TDE es una línea de 4861,06 angstroms. A la izquierda, el desplazamiento Doppler longitudinal da como resultado un ensanchamiento de la línea de emisión hasta tal punto que no se puede observar la TDE. Las figuras del medio ilustran que incluso si uno estrecha la vista al centro exacto del haz, desviaciones muy pequeñas del haz con respecto a un ángulo recto exacto introducen desplazamientos comparables al efecto previsto.

En lugar de intentar la medición directa de la TDE, Ives y Stilwell (1938) utilizaron un espejo cóncavo que les permitió observar simultáneamente un haz directo casi longitudinal (azul) y su imagen reflejada (roja). Espectroscópicamente, se observarían tres líneas: una línea de emisión no desplazada y líneas desplazadas al azul y al rojo. El promedio de las líneas desplazadas al rojo y al azul se compararía con la longitud de onda de la línea de emisión no desplazada. La diferencia que midieron Ives y Stilwell correspondía, dentro de los límites experimentales, al efecto predicho por la relatividad especial. ^{[p 7]}

Varias de las repeticiones posteriores del experimento de Ives y Stilwell han adoptado otras estrategias para medir la media de las emisiones de haces de partículas desplazadas hacia el azul y hacia el rojo. En algunas repeticiones recientes del experimento, se ha utilizado tecnología de aceleradores moderna para disponer la observación de dos haces de partículas que giran en sentido contrario. En otras repeticiones, se han medido las energías de los rayos gamma emitidos por un haz de partículas que se mueve rápidamente en ángulos opuestos con respecto a la dirección del haz de partículas. Dado que estos experimentos en realidad no miden la longitud de onda del haz de partículas en ángulos rectos con respecto al haz, algunos autores han preferido referirse al efecto que están midiendo como "desplazamiento Doppler cuadrático" en lugar de TDE. ^{[p 8] [p 9]}

Medición directa del efecto Doppler transversal

La aparición de la tecnología de los aceleradores de partículas ha hecho posible la producción de haces de partículas de una energía considerablemente superior a la que tenían a su disposición Ives y Stilwell. Esto ha permitido diseñar pruebas del efecto Doppler transversal siguiendo directamente la forma en que Einstein las imaginó originalmente, es decir, observando directamente un haz de partículas en un ángulo de 90°. Por ejemplo, Hasselkamp et al. (1979) observaron la línea H α emitida por átomos de hidrógeno que se movían a velocidades que iban desde 2,53×10 ⁸  cm/s hasta 9,28×10 ⁸  cm/s, y hallaron que el coeficiente del término de segundo orden en la aproximación relativista era 0,52 ± 0,03, en excelente acuerdo con el valor teórico de 1/2. ^{[p 10]}

Otras pruebas directas de la TDE en plataformas rotatorias fueron posibles gracias al descubrimiento del efecto Mössbauer , que permite la producción de líneas de resonancia extremadamente estrechas para la emisión y absorción de rayos gamma nucleares. ^[17] Los experimentos del efecto Mössbauer han demostrado ser fácilmente capaces de detectar la TDE utilizando velocidades relativas entre el emisor y el absorbente del orden de 2×10 ⁴  cm/s. Estos experimentos incluyen los realizados por Hay et al. (1960), ^{[p 11]} Champeney et al. (1965), ^{[p 12]} y Kündig (1963). ^{[p 3]}

Mediciones de dilatación del tiempo

El efecto Doppler transversal y la dilatación cinemática del tiempo de la relatividad especial están estrechamente relacionados. Todas las validaciones de TDE representan validaciones de la dilatación cinemática del tiempo, y la mayoría de las validaciones de la dilatación cinemática del tiempo también han representado validaciones de TDE. Un recurso en línea, "¿Cuál es la base experimental de la relatividad especial?", ha documentado, con breves comentarios, muchas de las pruebas que, a lo largo de los años, se han utilizado para validar varios aspectos de la relatividad especial. ^[18] Kaivola et al. (1985) ^{[pág. 13]} y McGowan et al. (1993) ^{[pág. 14]} son ​​ejemplos de experimentos clasificados en este recurso como experimentos de dilatación del tiempo. Estos dos también representan pruebas de TDE. Estos experimentos compararon la frecuencia de dos láseres, uno bloqueado a la frecuencia de una transición de átomo de neón en un haz rápido, el otro bloqueado a la misma transición en neón térmico. La versión de 1993 del experimento verificó la dilatación del tiempo, y por lo tanto la TDE, con una precisión de 2,3×10 ⁻⁶ .

Efecto Doppler relativista para el sonido y la luz

Figura 10. La fórmula relativista del desplazamiento Doppler es aplicable tanto al sonido como a la luz.

Los libros de texto de física de primer año analizan casi invariablemente el efecto Doppler del sonido en términos de la cinemática newtoniana, mientras que el efecto Doppler de la luz y los fenómenos electromagnéticos se analiza en términos de la cinemática relativista. Esto da la falsa impresión de que los fenómenos acústicos requieren un análisis diferente al de la luz y las ondas de radio.

El análisis tradicional del efecto Doppler para el sonido representa una aproximación de baja velocidad al análisis relativista exacto. El análisis completamente relativista para el sonido es, de hecho, igualmente aplicable tanto a los fenómenos sonoros como a los electromagnéticos.

Consideremos el diagrama espacio-temporal de la figura 10. En este diagrama se ilustran las líneas de mundo de un diapasón (la fuente) y de un receptor. El diapasón y el receptor comienzan en O, punto en el que el diapasón empieza a vibrar, emitiendo ondas y moviéndose a lo largo del eje x negativo mientras que el receptor empieza a moverse a lo largo del eje x positivo. El diapasón continúa hasta que llega a A, punto en el que deja de emitir ondas: por lo tanto, se ha generado un paquete de ondas y el receptor recibe todas las ondas del paquete de ondas y la última onda lo alcanza en B. El tiempo propio de la duración del paquete en el marco de referencia del diapasón es la longitud de OA, mientras que el tiempo propio de la duración del paquete de ondas en el marco de referencia del receptor es la longitud de OB. Si se emitieran ondas, entonces , mientras que ; la pendiente inversa de AB representa la velocidad de propagación de la señal (es decir, la velocidad del sonido) hasta el evento B . Por lo tanto, podemos escribir: ^[10] ${\displaystyle n}$ ${\displaystyle f_{s}={\frac {n}{|OA|}}}$ ${\displaystyle f_{r}={\frac {n}{|OB|}}}$

${\displaystyle c_{s}={\frac {x_{B}-x_{A}}{t_{B}-t_{A}}}}$(velocidad del sonido)

${\displaystyle v_{s}=-{\frac {x_{A}}{t_{A}}}}$        ${\displaystyle v_{r}={\frac {x_{B}}{t_{B}}}}$      (velocidades de la fuente y del receptor)

${\displaystyle |OA|={\sqrt {t_{A}^{2}-(x_{A}/c)^{2}}}}$

${\displaystyle |OB|={\sqrt {t_{B}^{2}-(x_{B}/c)^{2}}}}$

${\displaystyle v_{s}}$y se supone que son menores que, de lo contrario, su paso por el medio generará ondas de choque que invalidarán el cálculo. Algunas operaciones algebraicas rutinarias dan la relación de frecuencias: ${\displaystyle v_{r}}$ ${\displaystyle c_{s},}$

Ecuación 9:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {|OA|}{|OB|}}}$ ${\displaystyle ={\frac {1-v_{r}/c_{s}}{1+v_{s}/c_{s}}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

Si y son pequeños comparados con , la ecuación anterior se reduce a la fórmula Doppler clásica para el sonido. ${\displaystyle v_{r}}$ ${\displaystyle v_{s}}$ ${\displaystyle c}$

Si la velocidad de propagación de la señal se aproxima a , se puede demostrar que las velocidades absolutas y de la fuente y del receptor se fusionan en una única velocidad relativa independiente de cualquier referencia a un medio fijo. De hecho, obtenemos la ecuación 1 , la fórmula para el desplazamiento Doppler longitudinal relativista. ^[10] ${\displaystyle c_{s}}$ ${\displaystyle c}$ ${\displaystyle v_{s}}$ ${\displaystyle v_{r}}$

El análisis del diagrama de espacio-tiempo de la figura 10 proporcionó una fórmula general para la fuente y el receptor moviéndose directamente a lo largo de su línea de visión, es decir, en movimiento colineal.

Figura 11. Una fuente y un receptor se mueven en diferentes direcciones y velocidades en un marco donde la velocidad del sonido es independiente de la dirección.

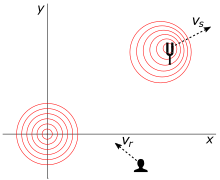
La figura 11 ilustra un escenario en dos dimensiones. La fuente se mueve con velocidad (en el momento de la emisión). Emite una señal que viaja a velocidad hacia el receptor, que viaja a velocidad en el momento de la recepción. El análisis se realiza en un sistema de coordenadas en el que la velocidad de la señal es independiente de la dirección. ^[6] ${\displaystyle \mathbf {v_{s}} }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \mathbf {v_{r}} }$ ${\displaystyle |\mathbf {C} |}$

La relación entre las frecuencias adecuadas para la fuente y el receptor es

Ecuación 10:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {1-{\frac {|\mathbf {v_{r}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{r}} })}{1-{\frac {|\mathbf {v_{s}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{s}} })}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

La razón principal tiene la forma del efecto Doppler clásico, mientras que el término de raíz cuadrada representa la corrección relativista. Si consideramos los ángulos relativos al marco de la fuente, entonces y la ecuación se reduce a la Ecuación 7 , la fórmula de Einstein de 1905 para el efecto Doppler. Si consideramos los ángulos relativos al marco del receptor, entonces y la ecuación se reduce a la Ecuación 6 , la forma alternativa de la ecuación de desplazamiento Doppler discutida previamente. ^[6] ${\displaystyle v_{s}=0}$ ${\displaystyle v_{r}=0}$

Véase también

• Efecto Doppler
• Efecto Doppler diferencial
• Transmisión relativista
• Desplazamiento al rojo
• Desplazamiento al azul
• Dilatación del tiempo
• Dilatación del tiempo gravitacional
• Relatividad especial

Notas

1. En su artículo seminal de 1905, en el que introdujo la relatividad especial, Einstein ya había publicado una expresión para el desplazamiento Doppler percibido por un observador que se mueve en un ángulo arbitrario con respecto a una fuente de luz infinitamente distante. La derivación de la EDT por parte de Einstein en 1907 representó una consecuencia trivial de su expresión general publicada anteriormente. ^{[p 2]}
2. Aquí, "intensidad de la fuente" se refiere a la intensidad espectral en frecuencia , es decir, potencia por unidad de ángulo sólido y por unidad de frecuencia, expresada en vatios por estereorradián por hercio; para la intensidad espectral en longitud de onda , el cubo debe reemplazarse por una quinta potencia.

Fuentes primarias

1. Einstein, Albert (1907). "Sobre la posibilidad de una nueva prueba del principio de relatividad (Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips)". Annalen der Physik . 328 (6): 197–198. Código bibliográfico : 1907AnP...328..197E. doi : 10.1002/andp.19073280613.
2. Einstein, Albert (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik (en alemán). 322 (10): 891–921. Código bibliográfico : 1905AnP...322..891E. doi : 10.1002/andp.19053221004 .Traducción al español: 'Sobre la electrodinámica de los cuerpos en movimiento'
3. Kündig, Walter (1963). "Medición del efecto Doppler transversal en un sistema acelerado". Physical Review . 129 (6): 2371–2375. Código Bibliográfico :1963PhRv..129.2371K. doi :10.1103/PhysRev.129.2371.
4. Champeney, DC; Moon, PB (1961). "Ausencia de desplazamiento Doppler para fuente y detector de rayos gamma en la misma órbita circular". Proc. Phys. Soc . 77 (2): 350–352. Bibcode :1961PPS....77..350C. doi :10.1088/0370-1328/77/2/318.
5. Synge, JL (1963). "Movimientos grupales en el espacio-tiempo y efectos Doppler". Nature . 198 (4881): 679. Bibcode :1963Natur.198..679S. doi : 10.1038/198679a0 . S2CID  42033531.
6. Johnson, Montgomery H.; Teller, Edward (febrero de 1982). "Cambios de intensidad en el efecto Doppler". Proc. Natl. Sci. USA . 79 (4): 1340. Bibcode :1982PNAS...79.1340J. doi : 10.1073/pnas.79.4.1340 . PMC 345964 . PMID  16593162. 
7. Ives, HE; ​​Stilwell, GR (1938). "Un estudio experimental de la velocidad de un reloj atómico en movimiento". Revista de la Sociedad Óptica de América . 28 (7): 215. Bibcode :1938JOSA...28..215I. doi :10.1364/JOSA.28.000215.
8. Olin, A.; Alexander, TK; Häusser, O.; McDonald, AB; Ewan, GT (1973). "Medición del efecto Doppler relativista utilizando rayos gamma de captura de 8,6 MeV". Phys. Rev. D . 8 (6): 1633–1639. Código Bibliográfico :1973PhRvD...8.1633O. doi :10.1103/PhysRevD.8.1633.
9. Mandelberg, Hirsch I.; Witten, Louis (1962). "Verificación experimental del efecto Doppler relativista". Revista de la Sociedad Óptica de América . 52 (5): 529–535. Código Bibliográfico :1962JOSA...52..529M. doi :10.1364/JOSA.52.000529.
10. Hasselkamp, ​​D.; Mondry, E.; Sharmann, A. (1979). "Observación directa del desplazamiento Doppler transversal". Zeitschrift für Physik A. 289 (2): 151-155. Código bibliográfico : 1979ZPhyA.289..151H. doi :10.1007/BF01435932. S2CID  120963034.
11. Hay, HJ; Schiffer, JP; Cranshaw, TE; Egelstaff, PA (1960). "Medición del desplazamiento hacia el rojo en un sistema acelerado utilizando el efecto Mössbauer en ⁵⁷ Fe". Physical Review Letters . 4 (4): 165–166. Código Bibliográfico :1960PhRvL...4..165H. doi :10.1103/PhysRevLett.4.165.
12. Champeney, DC; Isaak, GR; Khan, AM (1965). "Un experimento de dilatación del tiempo basado en el efecto Mössbauer". Actas de la Physical Society . 85 (3): 583–593. Bibcode :1965PPS....85..583C. doi :10.1088/0370-1328/85/3/317.
13. Kaivola, Matti; Riis, Erling; Lee, Siu Au (1985). "Medición del desplazamiento Doppler relativista en neón" (PDF) . Phys. Rev. Lett . 54 (4): 255–258. Bibcode :1985PhRvL..54..255K. doi :10.1103/PhysRevLett.54.255. PMID  10031461.
14. McGowan, Roger W.; Giltner, David M.; Sternberg, Scott J.; Lee, Siu Au (1993). "Nueva medición del efecto Doppler relativista en el neón". Phys. Rev. Lett . 70 (3): 251–254. Bibcode :1993PhRvL..70..251M. doi :10.1103/PhysRevLett.70.251. PMID  10054065.

Referencias

1. Daniel Kiefer (2014). Espejos electrónicos relativistas: a partir de interacciones entre láseres de alta intensidad y nanoláminas (edición ilustrada). Springer. pág. 22. ISBN 978-3-319-07752-9.Extracto de la página 22
2. Sher, D. (1968). "El efecto Doppler relativista". Revista de la Real Sociedad Astronómica de Canadá . 62 : 105–111. Código Bibliográfico :1968JRASC..62..105S . Consultado el 11 de octubre de 2018 .
3. Gill, TP (1965). El efecto Doppler . Londres: Logos Press Limited. págs. 6–9. OL  5947329M.
4. Feynman, Richard P. ; Leighton, Robert B. ; Sands, Matthew (febrero de 1977). "Efectos relativistas en la radiación". Las conferencias Feynman sobre física: volumen 1 . Reading, Massachusetts: Addison-Wesley . págs. 34–7 f. ISBN 9780201021165. Número de serie LCCN  2010938208.
5. Morin, David (2008). "Capítulo 11: Relatividad (Cinemática)" (PDF) . Introducción a la mecánica clásica: con problemas y soluciones . Cambridge University Press . págs. 539–543. ISBN. 978-1-139-46837-4. Archivado desde el original (PDF) el 4 de abril de 2018.
6. Brown, Kevin S. "El efecto Doppler". Mathpages . Consultado el 12 de octubre de 2018 .
7. Misner, CW, Thorne, KS y Wheeler, J. A (1973). Gravitación . Freeman. pág. 163. ISBN 978-0716703440.{{cite book}}: CS1 maint: multiple names: authors list (link)
8. Sama, Nicholas (1969). "Algunos comentarios sobre un experimento relativista de desplazamiento de frecuencia de Champeney y Moon". American Journal of Physics . 37 (8): 832–833. Bibcode :1969AmJPh..37..832S. doi :10.1119/1.1975859.
9. Keswani, GH (1965). Origen y concepto de la relatividad. Delhi, India: Alekh Prakashan. pp. 60–61 . Consultado el 13 de octubre de 2018 .
10. Brown, Kevin S. "Desplazamiento Doppler para el sonido y la luz". Mathpages . Consultado el 6 de agosto de 2015 .
11. Landau, LD ; Lifshitz, EM (2005). La teoría clásica de campos . Curso de física teórica: volumen 2. Trad. Morton Hamermesh (cuarta edición revisada en inglés). Elsevier Butterworth-Heinemann. págs. 116–117. ISBN 9780750627689.
12. Ta-Pei Cheng (2013). Física de Einstein: átomos, cuantos y relatividad: derivada, explicada y evaluada (edición ilustrada y reimpresa). OUP Oxford. pág. 164. ISBN 978-0-19-966991-2.Extracto de la página 164
13. Savage, CM; Searle, AC (1999). "Visualizing Special Relativity" (PDF) . The Physicist . 36 (141). Archivado desde el original (PDF) el 2008-08-03 . Consultado el 17 de octubre de 2018 .
14. Brandeker, Alexis. "¿Qué vería un viajero interestelar relativista?". Preguntas frecuentes sobre física . Departamento de Matemáticas, Universidad de California, Riverside. Archivado desde el original el 7 de mayo de 2021. Consultado el 17 de octubre de 2018 .
15. Kraus, U. (2000). "Brillo y color de objetos en rápido movimiento: La apariencia visual de una esfera grande revisada" (PDF) . Am. J. Phys . 68 (1): 56–60. Bibcode :2000AmJPh..68...56K. doi :10.1119/1.19373 . Consultado el 17 de octubre de 2018 .
16. Wright, Edward L. ("Ned"). "Errores en la cosmología de la luz cansada". Tutorial de cosmología de Ned Wright . Departamento de Astronomía, Universidad de California, Los Ángeles . Consultado el 17 de octubre de 2018 .
17. Saburo Nasu (2013). "Introducción general a la espectroscopia Mössbauer". En Yoshida, Yutaka; Langouche, Guido (eds.). Espectroscopia Mössbauer: libro tutorial . Springer. págs. 1–22. ISBN 978-3642322198.
18. Roberts, Tom; Schleif, Siegmar. "¿Cuál es la base experimental de la relatividad especial?". Preguntas frecuentes originales de Usenet sobre física . Departamento de Matemáticas, Universidad de California, Riverside . Consultado el 16 de octubre de 2018 .

Lectura adicional

• Moriconi, M (1 de noviembre de 2006). "Teoría especial de la relatividad a través del efecto Doppler". Revista Europea de Física . 27 (6): 1409–1423. arXiv : physics/0605204 . Código Bibliográfico :2006EJPh...27.1409M. doi :10.1088/0143-0807/27/6/015. S2CID  11347287.

Enlaces externos

• Simulador de relatividad especial Warp Programa de computadora que demuestra el efecto Doppler relativista.
• Kraus, Ute; Zahn, Corvin. "Viajes en el espacio-tiempo: visualización de la teoría de la relatividad". SpacetimeTravel.org . Grupo de Educación en Física y Astronomía, Universidad de Hildesheim, Alemania . Consultado el 17 de octubre de 2018 .