Un nomograma (del griego νόμος (nomos) 'ley' y γραμμή (grammē) 'línea'), también llamado nomograma , diagrama de alineación o ábac , es un dispositivo de cálculo gráfico , un diagrama bidimensional diseñado para permitir el cálculo gráfico aproximado de una función matemática . El campo de la nomografía fue inventado en 1884 por el ingeniero francés Philbert Maurice d'Ocagne (1862-1938) y se usó ampliamente durante muchos años para proporcionar a los ingenieros cálculos gráficos rápidos de fórmulas complicadas con una precisión práctica. Los nomogramas utilizan un sistema de coordenadas paralelas inventado por d'Ocagne en lugar de las coordenadas cartesianas estándar .
Un nomograma consiste en un conjunto de n escalas, una para cada variable de una ecuación. Conociendo los valores de n-1 variables, se puede encontrar el valor de la variable desconocida, o fijando los valores de algunas variables, se puede estudiar la relación entre las variables no fijadas. El resultado se obtiene colocando una regla sobre los valores conocidos de las escalas y leyendo el valor desconocido desde donde cruza la escala para esa variable. La línea virtual o dibujada creada por la regla se llama línea índice o isopleta .
Los nomogramas florecieron en muchos contextos diferentes durante aproximadamente 75 años porque permitían cálculos rápidos y precisos antes de la era de las calculadoras de bolsillo. Los resultados de un nomograma se obtienen de manera muy rápida y confiable simplemente dibujando una o más líneas. El usuario no tiene que saber cómo resolver ecuaciones algebraicas, buscar datos en tablas, usar una regla de cálculo o sustituir números en ecuaciones para obtener resultados. El usuario ni siquiera necesita saber la ecuación subyacente que representa el nomograma. Además, los nomogramas incorporan de manera natural el conocimiento del dominio implícito o explícito en su diseño. Por ejemplo, para crear nomogramas más grandes para una mayor precisión, el nomógrafo generalmente incluye solo rangos de escala que son razonables y de interés para el problema. Muchos nomogramas incluyen otras marcas útiles, como etiquetas de referencia y regiones coloreadas. Todas ellas proporcionan guías útiles para el usuario.

Al igual que una regla de cálculo, un nomograma es un dispositivo gráfico de cálculo analógico. También como una regla de cálculo, su precisión está limitada por la precisión con la que se pueden dibujar, reproducir, ver y alinear las marcas físicas. A diferencia de la regla de cálculo, que es un dispositivo de cálculo de uso general, un nomograma está diseñado para realizar un cálculo específico con tablas de valores integradas en las escalas del dispositivo . Los nomogramas se utilizan normalmente en aplicaciones para las que el nivel de precisión que proporcionan es suficiente y útil. Alternativamente, un nomograma se puede utilizar para comprobar una respuesta obtenida mediante un cálculo más exacto pero propenso a errores.
Otros tipos de calculadoras gráficas, como los diagramas de intersección , los diagramas trilineales y los diagramas hexagonales , a veces se denominan nomogramas. Estos dispositivos no cumplen con la definición de nomograma como calculadora gráfica cuya solución se encuentra mediante el uso de una o más isopletas lineales.

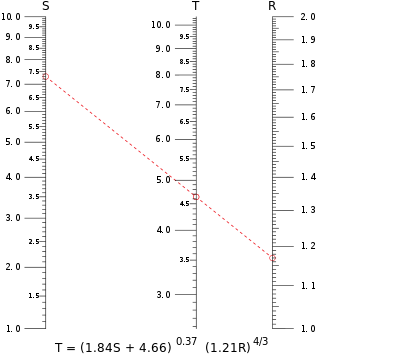
Un nomograma para una ecuación de tres variables normalmente tiene tres escalas, aunque existen nomogramas en los que dos o incluso las tres escalas son comunes. Aquí dos escalas representan valores conocidos y la tercera es la escala donde se lee el resultado. La ecuación más simple de este tipo es u 1 + u 2 + u 3 = 0 para las tres variables u 1 , u 2 y u 3 . A la derecha se muestra un ejemplo de este tipo de nomograma, anotado con los términos utilizados para describir las partes de un nomograma.
En ocasiones, las ecuaciones más complicadas pueden expresarse como la suma de funciones de las tres variables. Por ejemplo, el nomograma que aparece en la parte superior de este artículo podría construirse como un nomograma de escala paralela, ya que puede expresarse como una suma de este tipo después de tomar los logaritmos de ambos lados de la ecuación.
La escala de la variable desconocida puede estar entre las otras dos escalas o fuera de ellas. Los valores conocidos del cálculo se marcan en las escalas de esas variables y se traza una línea entre esas marcas. El resultado se lee en la escala desconocida en el punto donde la línea la cruza. Las escalas incluyen "marcas de verificación" para indicar las ubicaciones exactas de los números y también pueden incluir valores de referencia etiquetados. Estas escalas pueden ser lineales , logarítmicas o tener alguna relación más compleja.
La isopleta de muestra que se muestra en rojo en el nomograma que aparece en la parte superior de este artículo calcula el valor de T cuando S = 7,30 y R = 1,17. La isopleta cruza la escala de T justo por debajo de 4,65; una cifra más grande impresa en alta resolución en papel arrojaría T = 4,64 con una precisión de tres dígitos. Tenga en cuenta que cualquier variable se puede calcular a partir de los valores de las otras dos, una característica de los nomogramas que resulta particularmente útil para ecuaciones en las que una variable no se puede aislar algebraicamente de las otras variables.
Las escalas rectas son útiles para cálculos relativamente simples, pero para cálculos más complejos puede ser necesario el uso de escalas curvas simples o elaboradas. Se pueden construir nomogramas para más de tres variables incorporando una cuadrícula de escalas para dos de las variables o concatenando nomogramas individuales de un número menor de variables en un nomograma compuesto.
Los nomogramas se han utilizado en una amplia variedad de aplicaciones. Algunos ejemplos son:

El nomograma siguiente realiza el cálculo:
Este nomograma es interesante porque realiza un cálculo no lineal útil utilizando únicamente escalas rectas igualmente graduadas. Si bien la línea diagonal tiene una escala 10 veces mayor que la de los ejes, los números que figuran en ella coinciden exactamente con los que se encuentran directamente debajo o a su izquierda, por lo que se puede crear fácilmente dibujando una línea recta en diagonal sobre una hoja de papel cuadriculado .
A y B se introducen en las escalas horizontal y vertical, y el resultado se lee en la escala diagonal. Al ser proporcional a la media armónica de A y B , esta fórmula tiene varias aplicaciones. Por ejemplo, es la fórmula de resistencia paralela en electrónica y la ecuación de lente delgada en óptica .
En el ejemplo, la línea roja demuestra que las resistencias en paralelo de 56 y 42 ohmios tienen una resistencia combinada de 24 ohmios. También demuestra que un objeto a una distancia de 56 cm de una lente cuya distancia focal es de 24 cm forma una imagen real a una distancia de 42 cm.

El nomograma que se muestra a continuación se puede utilizar para realizar un cálculo aproximado de algunos valores necesarios al realizar una prueba estadística conocida, la prueba de chi-cuadrado de Pearson . Este nomograma demuestra el uso de escalas curvas con graduaciones espaciadas de manera desigual.
La expresión relevante es:
La escala que se muestra en la parte superior se comparte entre cinco rangos diferentes de valores observados: A, B, C, D y E. El valor observado se encuentra en uno de estos rangos y la marca de verificación que se utiliza en esa escala se encuentra inmediatamente por encima de él. Luego, se selecciona la escala curva que se utiliza para el valor esperado en función del rango. Por ejemplo, un valor observado de 9 utilizaría la marca de verificación que se encuentra por encima del 9 en el rango A y se utilizaría la escala curva A para el valor esperado. Un valor observado de 81 utilizaría la marca de verificación que se encuentra por encima de 81 en el rango E y se utilizaría la escala curva E para el valor esperado. Esto permite incorporar cinco nomogramas diferentes en un solo diagrama.
De esta manera, la línea azul demuestra el cálculo de:
(9 − 5) 2 / 5 = 3,2
y la línea roja demuestra el cálculo de:
(81 − 70) 2 / 70 = 1,7
Al realizar la prueba, se suele aplicar la corrección de Yates por continuidad , que simplemente implica restar 0,5 a los valores observados. Se podría construir un nomograma para realizar la prueba con la corrección de Yates simplemente desplazando cada escala "observada" media unidad hacia la izquierda, de modo que las graduaciones 1,0, 2,0, 3,0, ... se coloquen donde aparecen los valores 0,5, 1,5, 2,5, ... en el gráfico actual.

Aunque los nomogramas representan relaciones matemáticas, no todos se derivan matemáticamente. El siguiente nomograma se desarrolló gráficamente para lograr resultados finales apropiados que pudieran definirse fácilmente mediante el producto de sus relaciones en unidades subjetivas en lugar de numéricamente. El uso de ejes no paralelos permitió incorporar las relaciones no lineales al modelo.
Los números en recuadros indican los ejes que requieren entrada después de una evaluación apropiada.
El par de nomogramas en la parte superior de la imagen determina la probabilidad de ocurrencia y la disponibilidad, que luego se incorporan al nomograma multietapa inferior.
Las líneas 8 y 10 son «líneas de enlace» o «líneas de pivote» y se utilizan para la transición entre las etapas del nomograma compuesto.
El par final de escalas logarítmicas paralelas (12) no son nomogramas propiamente dichos, sino escalas de lectura para traducir la puntuación de riesgo (11, de remoto a extremadamente alto) en una frecuencia de muestreo para abordar aspectos de seguridad y otros aspectos de "protección del consumidor" respectivamente. Esta etapa requiere "aceptación" política para equilibrar el costo frente al riesgo. El ejemplo utiliza una frecuencia mínima de tres años para cada uno, aunque el extremo de alto riesgo de las escalas es diferente para los dos aspectos, lo que da frecuencias diferentes para los dos, pero ambos sujetos a un muestreo mínimo general de cada alimento para todos los aspectos al menos una vez cada tres años.
Este nomograma de evaluación de riesgos fue desarrollado por el Servicio de Análisis Público del Reino Unido con financiación de la Agencia de Normas Alimentarias del Reino Unido para su uso como herramienta para orientar la frecuencia adecuada de muestreo y análisis de alimentos para fines oficiales de control de alimentos, destinado a ser utilizado para evaluar todos los problemas potenciales con todos los alimentos, aunque todavía no se ha adoptado.
Usando una regla, se puede leer fácilmente el término faltante de la ley de los senos o las raíces de la ecuación cuadrática y cúbica . [4]