
El experimento Kennedy-Thorndike , realizado por primera vez en 1932 por Roy J. Kennedy y Edward M. Thorndike, es una forma modificada del procedimiento experimental de Michelson-Morley , que prueba la relatividad especial . [1] La modificación consiste en hacer que un brazo del aparato clásico de Michelson-Morley (MM) sea más corto que el otro. Mientras que el experimento de Michelson-Morley demostró que la velocidad de la luz es independiente de la orientación del aparato, el experimento de Kennedy-Thorndike demostró que también es independiente de la velocidad del aparato en diferentes marcos inerciales. También sirvió como prueba para verificar indirectamente la dilatación del tiempo : mientras que el resultado negativo del experimento de Michelson-Morley puede explicarse solo por la contracción de la longitud , el resultado negativo del experimento de Kennedy-Thorndike requiere dilatación del tiempo además de la contracción de la longitud para explicar por qué no se detectarán cambios de fase mientras la Tierra se mueve alrededor del Sol. La primera confirmación directa de la dilatación del tiempo se logró mediante el experimento de Ives-Stilwell . Combinando los resultados de esos tres experimentos, se puede derivar la transformación de Lorentz completa. [2]
Se han llevado a cabo variantes mejoradas del experimento Kennedy-Thorndike utilizando cavidades ópticas o medición de distancias por láser lunar . Para obtener una descripción general de las pruebas de invariancia de Lorentz , consulte Pruebas de relatividad especial .
El experimento original de Michelson-Morley fue útil únicamente para probar la hipótesis de la contracción de Lorentz-FitzGerald . Kennedy ya había realizado varias versiones cada vez más sofisticadas del experimento de MM a lo largo de la década de 1920, cuando se le ocurrió una manera de probar también la dilatación del tiempo . En sus propias palabras: [1]
El principio en que se basa este experimento es la simple proposición de que si un haz de luz homogénea se divide […] en dos haces que después de recorrer caminos de diferentes longitudes se vuelven a unir, entonces las fases relativas […] dependerán […] de la velocidad del aparato, a menos que la frecuencia de la luz dependa […] de la velocidad en la forma requerida por la relatividad.
En referencia a la Fig. 1, los componentes ópticos clave se montaron dentro de la cámara de vacío V sobre una base de cuarzo fundido de coeficiente de expansión térmica extremadamente bajo . Una camisa de agua W mantuvo la temperatura regulada dentro de 0,001 °C. La luz verde monocromática de una fuente de mercurio Hg pasó a través de un prisma polarizador de Nicol N antes de ingresar a la cámara de vacío y fue dividida por un divisor de haz B configurado en el ángulo de Brewster para evitar reflejos no deseados en la superficie trasera. Los dos haces se dirigieron hacia dos espejos M 1 y M 2 que se colocaron a distancias lo más divergentes posibles dada la longitud de coherencia de la línea de mercurio de 5461 Å (≈32 cm, lo que permite una diferencia en la longitud del brazo Δ L ≈ 16 cm). Los haces reflejados se recombinaron para formar franjas de interferencia circulares que se fotografiaron en P . Una rendija S permitió que se registraran múltiples exposiciones a lo largo del diámetro de los anillos en una sola placa fotográfica en diferentes momentos del día.
Al hacer que un brazo del experimento fuera mucho más corto que el otro, un cambio en la velocidad de la Tierra provocaría cambios en los tiempos de viaje de los rayos de luz, de lo que resultaría un desplazamiento de las franjas a menos que la frecuencia de la fuente de luz cambiara en el mismo grado. Para determinar si se producía dicho desplazamiento de las franjas , se hizo que el interferómetro fuera extremadamente estable y se fotografiaron los patrones de interferencia para compararlos más tarde. Las pruebas se realizaron durante un período de muchos meses. Como no se encontró ningún desplazamiento de las franjas significativo (que corresponde a una velocidad de 10 ± 10 km/s dentro del margen de error), los experimentadores concluyeron que la dilatación del tiempo se produce como predice la relatividad especial.
Aunque la contracción de Lorentz-FitzGerald (contracción de Lorentz) por sí sola es totalmente capaz de explicar los resultados nulos del experimento de Michelson-Morley, no es capaz de explicar por sí sola los resultados nulos del experimento de Kennedy-Thorndike. La contracción de Lorentz-FitzGerald viene dada por la fórmula:
dónde
y el factor de Lorentz se define como
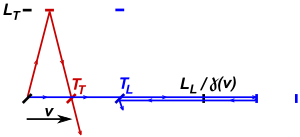
La figura 2 ilustra un aparato de Kennedy-Thorndike con brazos perpendiculares y supone la validez de la contracción de Lorentz. [3] Si el aparato está inmóvil con respecto al éter hipotético, la diferencia de tiempo que tarda la luz en atravesar los brazos longitudinales y transversales viene dada por:
El tiempo que tarda la luz en recorrer de ida y vuelta la longitud contraída por Lorentz del brazo longitudinal viene dado por:
donde T 1 es el tiempo de recorrido en la dirección del movimiento, T 2 en la dirección opuesta, v es el componente de velocidad con respecto al éter luminífero, c es la velocidad de la luz y L L la longitud del brazo longitudinal del interferómetro. El tiempo que tarda la luz en atravesar y volver del brazo transversal viene dado por:
La diferencia de tiempo que tarda la luz en atravesar los brazos longitudinales y transversales viene dada por:
Como Δ L=c(T L -T T ) , se dan las siguientes diferencias de longitud de recorrido ( siendo Δ L A la diferencia de longitud de recorrido inicial y v A la velocidad inicial del aparato, y Δ L B y v B después de la rotación o cambio de velocidad debido a la propia rotación de la Tierra o su rotación alrededor del Sol): [4]
Para obtener un resultado negativo, deberíamos tener Δ L A −Δ L B = 0. Sin embargo, se puede ver que ambas fórmulas solo se cancelan entre sí mientras las velocidades sean las mismas ( v A = v B ). Pero si las velocidades son diferentes, entonces Δ L A y Δ L B ya no son iguales. (El experimento de Michelson-Morley no se ve afectado por los cambios de velocidad ya que la diferencia entre L L y L T es cero. Por lo tanto, el experimento MM solo prueba si la velocidad de la luz depende de la orientación del aparato). Pero en el experimento de Kennedy-Thorndike, las longitudes L L y L T son diferentes desde el principio, por lo que también es capaz de medir la dependencia de la velocidad de la luz con la velocidad del aparato. [2]
De acuerdo con la fórmula anterior, la diferencia de longitud de recorrido Δ L A −Δ L B y, en consecuencia, el desplazamiento de franja esperado Δ N se dan por (siendo λ la longitud de onda):
Despreciando magnitudes superiores al segundo orden en v/c :
Para que Δ N sea constante , es decir , para que el desplazamiento de la franja sea independiente de la velocidad o la orientación del aparato, es necesario que la frecuencia y, por lo tanto, la longitud de onda λ se modifiquen mediante el factor de Lorentz. Este es realmente el caso cuando se considera el efecto de la dilatación del tiempo sobre la frecuencia. Por lo tanto, se requieren tanto la contracción de la longitud como la dilatación del tiempo para explicar el resultado negativo del experimento de Kennedy-Thorndike.
En 1905, Henri Poincaré y Albert Einstein habían demostrado que la transformación de Lorentz debe formar un grupo para satisfacer el principio de relatividad (véase Historia de las transformaciones de Lorentz ). Esto requiere que la contracción de la longitud y la dilatación del tiempo tengan los valores relativistas exactos. Kennedy y Thorndike argumentaron ahora que podían derivar la transformación de Lorentz completa únicamente a partir de los datos experimentales del experimento de Michelson-Morley y el experimento de Kennedy-Thorndike. Pero esto no es estrictamente correcto, ya que la contracción de la longitud y la dilatación del tiempo que tienen sus valores relativistas exactos son suficientes pero no necesarios para la explicación de ambos experimentos. Esto se debe a que la contracción de la longitud únicamente en la dirección del movimiento es solo una posibilidad para explicar el experimento de Michelson-Morley. En general, su resultado nulo requiere que la relación entre las longitudes transversales y longitudinales corresponda al factor de Lorentz, que incluye infinitas combinaciones de cambios de longitud en la dirección transversal y longitudinal. Esto también afecta el papel de la dilatación del tiempo en el experimento de Kennedy-Thorndike, porque su valor depende del valor de la contracción de longitud utilizada en el análisis del experimento. Por lo tanto, es necesario considerar un tercer experimento, el experimento de Ives-Stilwell , para derivar la transformación de Lorentz a partir de datos experimentales únicamente. [2]
Más precisamente: En el marco de la teoría de la prueba de Robertson-Mansouri-Sexl , [2] [5] se puede utilizar el siguiente esquema para describir los experimentos: α representa los cambios de tiempo, β los cambios de longitud en la dirección del movimiento y δ los cambios de longitud perpendiculares a la dirección del movimiento. El experimento de Michelson-Morley prueba la relación entre β y δ, mientras que el experimento de Kennedy-Thorndike prueba la relación entre α y β. Por lo tanto, α depende de β, que a su vez depende de δ, y solo se pueden medir combinaciones de esas cantidades, pero no sus valores individuales, en estos dos experimentos. Es necesario otro experimento para medir directamente el valor de una de estas cantidades. Esto se logró realmente con el experimento de Ives-Stilwell, que midió que α tenía el valor predicho por la dilatación del tiempo relativista. La combinación de este valor para α con el resultado nulo de Kennedy-Thorndike muestra que β necesariamente debe asumir el valor de la contracción de la longitud relativista. Y al combinar este valor de β con el resultado nulo de Michelson-Morley se demuestra que δ debe ser cero. Por lo tanto, los componentes necesarios de la transformación de Lorentz se proporcionan experimentalmente, de acuerdo con los requisitos teóricos de la teoría de grupos .
En los últimos años, los experimentos de Michelson-Morley , así como los experimentos de tipo Kennedy-Thorndike, se han repetido con mayor precisión utilizando láseres , máseres y resonadores ópticos criogénicos . Los límites de dependencia de la velocidad según la teoría de prueba de Robertson-Mansouri-Sexl (RMS), que indica la relación entre la dilatación del tiempo y la contracción de la longitud, se han mejorado significativamente. Por ejemplo, el experimento original de Kennedy-Thorndike estableció límites en la dependencia de la velocidad RMS de ~10 −2 , pero los límites actuales están en el rango de ~10 −8 . [5]
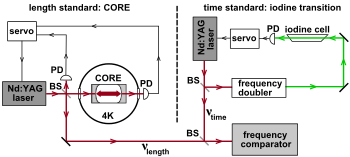
La figura 3 presenta un diagrama esquemático simplificado de la repetición del experimento Kennedy-Thorndike de Braxmaier et al . en 2002. [6] A la izquierda, los fotodetectores (PD) monitorean la resonancia de un patrón de longitud de resonador óptico criogénico (CORE) de zafiro mantenido a temperatura de helio líquido para estabilizar la frecuencia de un láser Nd:YAG a 1064 nm. A la derecha, la línea de absorbancia de 532 nm de una referencia de yodo a baja presión se utiliza como patrón de tiempo para estabilizar la frecuencia (duplicada) de un segundo láser Nd:YAG.
Además de las mediciones terrestres, Müller y Soffel (1995) [11] y Müller et al. (1999) [12] llevaron a cabo experimentos de Kennedy-Thorndike utilizando datos de medición de distancia por láser lunar , en los que la distancia Tierra-Luna se evalúa con una precisión de centímetros. Si hay un marco de referencia preferido y la velocidad de la luz depende de la velocidad del observador, entonces deberían observarse oscilaciones anómalas en las mediciones de distancia Tierra-Luna. Dado que la dilatación del tiempo ya está confirmada con alta precisión, la observación de tales oscilaciones demostraría la dependencia de la velocidad de la luz con respecto a la velocidad del observador, así como la dependencia de la dirección de la contracción de la longitud. Sin embargo, no se observaron tales oscilaciones en ninguno de los estudios, con un límite de velocidad RMS de ~10 −5 , [12] comparable a los límites establecidos por Hils y Hall (1990). Por lo tanto, tanto la contracción de la longitud como la dilatación del tiempo deben tener los valores predichos por la relatividad.
{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )