Los flujos turbulentos son movimientos caóticos y multiescalar complejos que deben clasificarse en componentes más elementales, denominados estructuras turbulentas coherentes . Dicha estructura debe tener coherencia temporal, es decir, debe persistir en su forma durante períodos lo suficientemente largos como para que se puedan aplicar los métodos de estadísticas promediadas en el tiempo. Las estructuras coherentes se estudian típicamente en escalas muy grandes, pero se pueden descomponer en estructuras más elementales con propiedades coherentes propias; tales ejemplos incluyen vórtices de horquilla. Las horquillas y las estructuras coherentes se han estudiado y observado en los datos desde la década de 1930, y desde entonces se han citado en miles de artículos y revisiones científicas. [1]

Los experimentos de visualización de flujo , utilizando humo y tinte como trazadores, se han utilizado históricamente para simular estructuras coherentes y verificar teorías, pero los modelos informáticos son ahora las herramientas dominantes ampliamente utilizadas en el campo para verificar y comprender la formación, evolución y otras propiedades de dichas estructuras. Las propiedades cinemáticas de estos movimientos incluyen tamaño, escala, forma, vorticidad , energía y las propiedades dinámicas gobiernan la forma en que las estructuras coherentes crecen, evolucionan y decaen. La mayoría de las estructuras coherentes se estudian solo dentro de las formas confinadas de turbulencia de pared simple, que se aproxima a la coherencia como estable, completamente desarrollada, incompresible y con un gradiente de presión cero en la capa límite . Aunque tales aproximaciones se alejan de la realidad, contienen suficientes parámetros necesarios para comprender las estructuras coherentes turbulentas en un grado altamente conceptual. [2]
La presencia de movimientos y estructuras organizados en flujos de cizallamiento turbulentos fue evidente durante mucho tiempo, y ha sido implicada adicionalmente por la hipótesis de longitud de mezcla incluso antes de que el concepto se estableciera explícitamente en la literatura. También hubo datos de correlación tempranos encontrados mediante la medición de chorros y estelas turbulentas, particularmente por Corrsin y Roshko. La técnica de burbuja de hidrógeno de Hama, que utilizó la visualización del flujo para observar las estructuras, recibió una amplia atención y muchos investigadores la siguieron, incluido Kline. La visualización del flujo es una técnica experimental de laboratorio que se utiliza para visualizar y comprender las estructuras de los flujos de cizallamiento turbulentos . [1] Con una comprensión mucho mejor de las estructuras coherentes, ahora es posible descubrir y reconocer muchas estructuras coherentes en imágenes de visualización de flujo anteriores recopiladas de varios flujos turbulentos tomadas hace décadas. Las simulaciones por computadora ahora son la herramienta dominante para comprender y visualizar estructuras de flujo coherente. La capacidad de calcular las ecuaciones de Navier-Stokes dependientes del tiempo necesarias produce presentaciones gráficas a un nivel mucho más sofisticado y, además, pueden visualizarse en diferentes planos y resoluciones, superando los tamaños y velocidades esperados generados anteriormente en experimentos de laboratorio. Sin embargo, los experimentos de visualización de flujo controlado siguen siendo necesarios para dirigir, desarrollar y validar las simulaciones numéricas que ahora dominan en el campo. [2]
Un flujo turbulento es un régimen de flujo en dinámica de fluidos donde la velocidad del fluido varía significativa e irregularmente tanto en posición como en tiempo. [3] Además, una estructura coherente se define como un flujo turbulento cuya expresión de vorticidad, que generalmente es estocástica, contiene componentes ordenados que pueden describirse como instantáneamente coherentes en la extensión espacial de la estructura de flujo. En otras palabras, subyacente a las expresiones de vorticidad caótica tridimensional típicas de los flujos turbulentos, hay un componente organizado de esa vorticidad que está correlacionado en fase en todo el espacio de la estructura. La vorticidad instantáneamente correlacionada en fase y espacio que se encuentra dentro de las expresiones de estructura coherente se puede definir como vorticidad coherente, lo que hace que la vorticidad coherente sea el principal identificador característico de las estructuras coherentes. Otra característica inherente a los flujos turbulentos es su intermitencia , pero la intermitencia es un identificador muy pobre de los límites de una estructura coherente, por lo tanto, se acepta generalmente que la mejor manera de caracterizar el límite de una estructura es identificando y definiendo el límite de la vorticidad coherente. [2]
Al definir e identificar la estructura coherente de esta manera, los flujos turbulentos se pueden descomponer en estructuras coherentes y estructuras incoherentes según su coherencia, en particular sus correlaciones con su vorticidad. Por lo tanto, los eventos organizados de manera similar en un promedio de conjunto de eventos organizados se pueden definir como una estructura coherente, y cualquier evento que no se identifique como similar o alineado en fase y espacio en el promedio de conjunto es una estructura turbulenta incoherente.
Otros intentos de definir una estructura coherente pueden realizarse examinando la correlación entre sus momentos o presión y sus flujos turbulentos. Sin embargo, a menudo conduce a indicaciones falsas de turbulencia, ya que las fluctuaciones de presión y velocidad sobre un fluido podrían estar bien correlacionadas en ausencia de turbulencia o vorticidad. Algunas estructuras coherentes, como anillos de vórtices , etc., pueden ser movimientos a gran escala comparables a la extensión del flujo de corte. También hay movimientos coherentes a escalas mucho más pequeñas, como vórtices de horquilla y remolinos típicos, que generalmente se conocen como subestructuras coherentes, como en las estructuras coherentes que se pueden dividir en subestructuras más pequeñas y elementales.
Aunque una estructura coherente se caracteriza por definición por altos niveles de vorticidad coherente, tensión de Reynolds , producción y transporte de calor y masa, no necesariamente requiere un alto nivel de energía cinética. De hecho, una de las principales funciones de las estructuras coherentes es el transporte a gran escala de masa, calor y momento sin requerir las altas cantidades de energía que normalmente se necesitan. En consecuencia, esto implica que las estructuras coherentes no son la principal producción y causa de la tensión de Reynolds, y la turbulencia incoherente puede ser igualmente significativa. [4]
Las estructuras coherentes no se pueden superponer , es decir, no se pueden superponer y cada estructura coherente tiene su propio dominio y límite independientes. Dado que los remolinos coexisten como superposiciones espaciales, una estructura coherente no es un remolino . Por ejemplo, los remolinos disipan energía obteniendo energía del flujo medio a grandes escalas y, finalmente, disipándola a las escalas más pequeñas. No existe tal intercambio análogo de energía entre estructuras coherentes, y cualquier interacción como el desgarro entre estructuras coherentes simplemente da como resultado una nueva estructura. Sin embargo, dos estructuras coherentes pueden interactuar e influirse mutuamente. La masa de una estructura cambia con el tiempo, y el caso típico es que las estructuras aumentan de volumen a través de la difusión de la vorticidad.
Una de las magnitudes más fundamentales de las estructuras coherentes se caracteriza por la vorticidad coherente, . Quizás las siguientes medidas más críticas de las estructuras coherentes sean las tensiones de Reynolds coherentes e incoherentes, y . Estas representan los transportes de momento, y su fuerza relativa indica cuánto momento está siendo transportado por las estructuras coherentes en comparación con las estructuras incoherentes. Las siguientes medidas más significativas incluyen representaciones contorneadas de la tasa de deformación coherente y la producción de cizallamiento. Una propiedad útil de tales contornos es que son invariantes bajo las transformaciones galileanas, por lo tanto, los contornos de vorticidad coherente constituyen un excelente identificador de los límites de la estructura. Los contornos de estas propiedades no solo ubican exactamente dónde las magnitudes de la estructura coherente tienen sus picos y sus puntos de apoyo, sino que también identifican dónde están las estructuras turbulentas incoherentes cuando se superponen en sus gradientes direccionales. Además, se pueden dibujar contornos espaciales que describan la forma, el tamaño y la resistencia de las estructuras coherentes, mostrando no solo la mecánica sino también la evolución dinámica de las estructuras coherentes. Por ejemplo, para que una estructura esté evolucionando y, por lo tanto, sea dominante, su vorticidad coherente, su tensión de Reynolds coherente y sus términos de producción deben ser mayores que los valores promedio en el tiempo de las estructuras de flujo. [2]
Las estructuras coherentes se forman debido a algún tipo de inestabilidad, por ejemplo, la inestabilidad de Kelvin-Helmholtz . Identificar una inestabilidad, y por lo tanto la formación inicial de una estructura coherente, requiere el conocimiento de las condiciones iniciales de la estructura de flujo. Por lo tanto, la documentación de la condición inicial es esencial para capturar la evolución y las interacciones de las estructuras coherentes, ya que las condiciones iniciales son bastante variables. Pasar por alto las condiciones iniciales era común en los primeros estudios debido a que los investigadores pasaban por alto su importancia. Las condiciones iniciales incluyen el perfil de velocidad media, el espesor, la forma, las densidades de probabilidad de velocidad y momento, el espectro de valores de tensión de Reynolds, etc. Estas medidas de las condiciones de flujo iniciales se pueden organizar y agrupar en tres amplias categorías: laminar , altamente perturbado y completamente turbulento. [2]
De las tres categorías, las estructuras coherentes surgen típicamente de inestabilidades en estados laminares o turbulentos. Después de un desencadenamiento inicial, su crecimiento está determinado por cambios evolutivos debidos a interacciones no lineales con otras estructuras coherentes, o su descomposición en estructuras turbulentas incoherentes. Los cambios rápidos observados llevan a la creencia de que debe haber un ciclo regenerativo que tiene lugar durante la descomposición. Por ejemplo, después de que una estructura se desintegra, el resultado puede ser que el flujo ahora sea turbulento y se vuelva susceptible a una nueva inestabilidad determinada por el nuevo estado de flujo, lo que lleva a la formación de una nueva estructura coherente. También es posible que las estructuras no se desintegran y, en cambio, se distorsionen al dividirse en subestructuras o interactuar con otras estructuras coherentes.
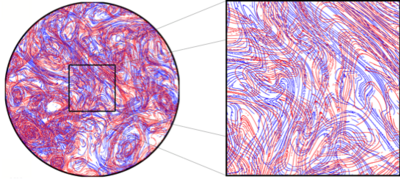
Las estructuras coherentes lagrangianas (LCS) son superficies materiales influyentes que crean patrones claramente reconocibles en distribuciones de trazadores pasivos transportados por un flujo inestable. Las LCS se pueden clasificar como hiperbólicas (superficies materiales que atraen o repelen al máximo localmente), elípticas (límites de vórtices materiales) y parabólicas (núcleos de chorros materiales). Estas superficies son generalizaciones de variedades invariantes clásicas, conocidas en la teoría de sistemas dinámicos , a datos de flujo inestable de tiempo finito. Esta perspectiva lagrangiana sobre la coherencia se ocupa de las estructuras formadas por elementos fluidos, a diferencia de la noción euleriana de coherencia, que considera características en el campo de velocidad instantánea del fluido. Se han desarrollado varias técnicas matemáticas para identificar LCS en conjuntos de datos bidimensionales y tridimensionales, y se han aplicado a experimentos de laboratorio, simulaciones numéricas y observaciones geofísicas. [6] [7]
Los vórtices en horquilla se encuentran en la parte superior de los bultos turbulentos de la pared turbulenta, [8] envolviéndolos en bucles con forma de horquilla, de donde se origina el nombre. Se cree que los vórtices en forma de horquilla son uno de los patrones de flujo sostenido más importantes y elementales en las capas límite turbulentas. Las horquillas son quizás las estructuras más simples, y los modelos que representan capas límite turbulentas a gran escala a menudo se construyen descomponiendo vórtices en horquilla individuales, lo que podría explicar la mayoría de las características de la turbulencia en la pared. Aunque los vórtices en horquilla forman la base de modelos conceptuales simples de flujo cerca de una pared, los flujos turbulentos reales pueden contener una jerarquía de vórtices en competencia, cada uno con su propio grado de asimetría y perturbaciones. [9]
Los vórtices en horquilla se parecen al vórtice en herradura, que existe debido a perturbaciones de pequeños movimientos ascendentes debido a diferencias en las velocidades de flujo ascendente dependiendo de la distancia desde la pared. Estos forman múltiples paquetes de vórtices en horquilla, donde los paquetes de horquilla de diferentes tamaños podrían generar nuevos vórtices para agregar al paquete. Específicamente, cerca de la superficie, los extremos de cola de los vórtices en horquilla podrían converger gradualmente dando como resultado erupciones provocadas, produciendo nuevos vórtices en horquilla. Por lo tanto, tales erupciones son un proceso regenerativo, en el que actúan para crear vórtices cerca de la superficie y expulsarlos hacia las regiones externas de la pared turbulenta. Con base en las propiedades eruptivas, se puede inferir que estos flujos son muy eficientes en la transferencia de calor debido a la mezcla. Específicamente, las erupciones transportan fluidos calientes hacia arriba mientras que los flujos más fríos son llevados hacia abajo durante la convergencia de las colas de los vórtices en horquilla antes de la erupción. [10]
Se cree que la producción y las contribuciones a la tensión de Reynolds ocurren durante interacciones fuertes entre las paredes internas y externas de las horquillas. Durante la producción de este término de tensión de Reynolds, las contribuciones se producen en segmentos de tiempo intermitentes y agudos cuando las erupciones traen nuevos vórtices hacia afuera.
La formación de vórtices en horquilla se ha observado en experimentos y simulaciones numéricas de horquillas individuales, sin embargo, la evidencia observacional de su existencia en la naturaleza aún es limitada. Theodorsen ha estado produciendo bocetos que indican la presencia de vórtices en horquilla en sus experimentos de visualización de flujo. Estas estructuras elementales más pequeñas se pueden ver superpuestas al vórtice principal en el boceto de la derecha (imagen del boceto del experimento de vapor de Theodorsen que expone la presencia de estructuras). El boceto era muy avanzado para la época, pero con la llegada de las computadoras llegaron mejores representaciones. En 1952, Robinson aisló dos tipos de estructuras de flujo que llamó vórtice en "herradura" o arco y vórtice "cuasi-fluyente" (figura clásica que se muestra a la derecha). [1]

Desde el uso masivo de las computadoras, las simulaciones numéricas directas o DNS se han utilizado ampliamente, produciendo vastos conjuntos de datos que describen la compleja evolución del flujo. DNS indica que muchos vórtices tridimensionales complejos están incrustados en regiones de alto esfuerzo cortante cerca de la superficie. Los investigadores buscan en esta región de alto esfuerzo cortante indicios de estructuras de vórtices individuales basadas en definiciones aceptadas, como vórtices coherentes. Históricamente, se ha pensado en un vórtice como una región en el flujo donde un grupo de líneas de vórtice se unen, lo que indica la presencia de un núcleo de vórtice, con grupos de trayectorias circulares instantáneas alrededor del núcleo. En 1991, Robinson definió una estructura de vórtice como un núcleo que consiste en regiones de baja presión convectivas, donde las líneas de corriente instantáneas pueden formar círculos o formas espirales en relación con el plano normal al plano del núcleo del vórtice. Aunque no es posible rastrear la evolución de las horquillas durante largos períodos, es posible identificar y rastrear su evolución durante períodos de tiempo cortos. Algunas de las características clave notables de los vórtices de horquilla son cómo interactúan con el flujo de corte de fondo, otros vórtices y cómo interactúan con el flujo cerca de la superficie. [1]